Self-Similarity of the Mandelbrot Set
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

On the Mandelbrot Set for I2 = ±1 and Imaginary Higgs Fields
Journal of Advances in Applied Mathematics, Vol. 6, No. 2, April 2021 https://dx.doi.org/10.22606/jaam.2021.62001 27 On the Mandelbrot Set for i2 = ±1 and Imaginary Higgs Fields Jonathan Blackledge Stokes Professor, Science Foundation Ireland. Distinguished Professor, Centre for Advanced Studies, Warsaw University of Technology, Poland. Visiting Professor, Faculty of Arts, Science and Technology, Wrexham Glyndwr University of Wales, UK. Professor Extraordinaire, Faculty of Natural Sciences, University of Western Cape, South Africa. Honorary Professor, School of Electrical and Electronic Engineering, Technological University Dublin, Ireland. Honorary Professor, School of Mathematics, Statistics and Computer Science, University of KwaZulu-Natal, South Africa. Email: [email protected] Abstract We consider the consequence√ of breaking with a fundamental result in complex analysis by letting i2 = ±1 where i = −1 is the basic unit of all imaginary numbers. An analysis of the Mandelbrot set for this case shows that a demarcation between a Fractal and a Euclidean object is possible based on i2 = −1 and i2 = +1, respectively. Further, we consider the transient behaviour associated with the two cases to produce a range of non-standard sets in which a Fractal geometric structure is transformed into a Euclidean object. In the case of the Mandelbrot set, the Euclidean object is a square whose properties are investigate. Coupled with the associated Julia sets and other complex plane mappings, this approach provides the potential to generate a wide range of new semi-fractal structures which are visually interesting and may be of artistic merit. In this context, we present a mathematical paradox which explores the idea that i2 = ±1. -

ABSTRACT Chaos in Dendritic and Circular Julia Sets Nathan Averbeck, Ph.D. Advisor: Brian Raines, D.Phil. We Demonstrate The
ABSTRACT Chaos in Dendritic and Circular Julia Sets Nathan Averbeck, Ph.D. Advisor: Brian Raines, D.Phil. We demonstrate the existence of various forms of chaos (including transitive distributional chaos, !-chaos, topological chaos, and exact Devaney chaos) on two families of abstract Julia sets: the dendritic Julia sets Dτ and the \circular" Julia sets Eτ , whose symbolic encoding was introduced by Stewart Baldwin. In particular, suppose one of the two following conditions hold: either fc has a Julia set which is a dendrite, or (provided that the kneading sequence of c is Γ-acceptable) that fc has an attracting or parabolic periodic point. Then, by way of a conjugacy which allows us to represent these Julia sets symbolically, we prove that fc exhibits various forms of chaos. Chaos in Dendritic and Circular Julia Sets by Nathan Averbeck, B.S., M.A. A Dissertation Approved by the Department of Mathematics Lance L. Littlejohn, Ph.D., Chairperson Submitted to the Graduate Faculty of Baylor University in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy Approved by the Dissertation Committee Brian Raines, D.Phil., Chairperson Will Brian, D.Phil. Markus Hunziker, Ph.D. Alexander Pruss, Ph.D. David Ryden, Ph.D. Accepted by the Graduate School August 2016 J. Larry Lyon, Ph.D., Dean Page bearing signatures is kept on file in the Graduate School. Copyright c 2016 by Nathan Averbeck All rights reserved TABLE OF CONTENTS LIST OF FIGURES vi ACKNOWLEDGMENTS vii DEDICATION viii 1 Preliminaries 1 1.1 Continuum Theory and Dynamical Systems . 1 1.2 Unimodal Maps . -

Finite Subdivision Rules from Matings of Quadratic Functions: Existence and Constructions
Finite Subdivision Rules from Matings of Quadratic Functions: Existence and Constructions Mary E. Wilkerson Dissertation submitted to the Faculty of the Virginia Polytechnic Institute and State University in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Mathematics William J. Floyd, Chair Peter E. Haskell Leslie D. Kay John F. Rossi April 24, 2012 Blacksburg, Virginia Keywords: Finite Subdivision Rules, Matings, Hubbard Trees, Combinatorial Dynamics Copyright 2012, Mary E. Wilkerson Finite Subdivision Rules from Matings of Quadratic Functions Mary E. Wilkerson (ABSTRACT) Combinatorial methods are utilized to examine preimage iterations of topologically glued polynomials. In particular, this paper addresses using finite subdivision rules and Hubbard trees as tools to model the dynamic behavior of mated quadratic functions. Several methods of construction of invariant structures on modified degenerate matings are detailed, and examples of parameter-based families of matings for which these methods succeed (and fail) are given. Acknowledgments There are several wonderful, caring, and helpful people who deserve the greatest of my appreciation for helping me through this document and for my last several years at Virginia Tech: • My family and friends, I owe you thanks for your love and support. • Robert and the Tolls of Madness, thank you for keeping me sane by providing an outlet to help me get away from grad school every now and then. • All of my previous mentors and professors in the VT Math Department, I can't express how far I feel that I've come thanks to the opportunities you've given me to learn and grow. Thank you all for giving me a chance and guiding me to where I am today. -

On the Numerical Construction Of
ON THE NUMERICAL CONSTRUCTION OF HYPERBOLIC STRUCTURES FOR COMPLEX DYNAMICAL SYSTEMS A Dissertation Presented to the Faculty of the Graduate School of Cornell University in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy by Jennifer Suzanne Lynch Hruska August 2002 c 2002 Jennifer Suzanne Lynch Hruska ALL RIGHTS RESERVED ON THE NUMERICAL CONSTRUCTION OF HYPERBOLIC STRUCTURES FOR COMPLEX DYNAMICAL SYSTEMS Jennifer Suzanne Lynch Hruska, Ph.D. Cornell University 2002 Our main interest is using a computer to rigorously study -pseudo orbits for polynomial diffeomorphisms of C2. Periodic -pseudo orbits form the -chain re- current set, R. The intersection ∩>0R is the chain recurrent set, R. This set is of fundamental importance in dynamical systems. Due to the theoretical and practical difficulties involved in the study of C2, computers will presumably play a role in such efforts. Our aim is to use computers not only for inspiration, but to perform rigorous mathematical proofs. In this dissertation, we develop a computer program, called Hypatia, which locates R, sorts points into components according to their -dynamics, and inves- tigates the property of hyperbolicity on R. The output is either “yes”, in which case the computation proves hyperbolicity, or “not for this ”, in which case infor- mation is provided on numerical or dynamical obstructions. A diffeomorphism f is hyperbolic on a set X if for each x there is a splitting of the tangent bundle of x into an unstable and a stable direction, with the unstable (stable) direction expanded by f (f −1). A diffeomorphism is hyperbolic if it is hyperbolic on its chain recurrent set. -

Fast Visualisation and Interactive Design of Deterministic Fractals
Computational Aesthetics in Graphics, Visualization, and Imaging (2008) P. Brown, D. W. Cunningham, V. Interrante, and J. McCormack (Editors) Fast Visualisation and Interactive Design of Deterministic Fractals Sven Banisch1 & Mateu Sbert2 1Faculty of Media, Bauhaus–University Weimar, D-99421 Weimar (GERMANY) 2Department of Informàtica i Matemàtica Aplicada, University of Girona, 17071 Girona (SPAIN) Abstract This paper describes an interactive software tool for the visualisation and the design of artistic fractal images. The software (called AttractOrAnalyst) implements a fast algorithm for the visualisation of basins of attraction of iterated function systems, many of which show fractal properties. It also presents an intuitive technique for fractal shape exploration. Interactive visualisation of fractals allows that parameter changes can be applied at run time. This enables real-time fractal animation. Moreover, an extended analysis of the discrete dynamical systems used to generate the fractal is possible. For a fast exploration of different fractal shapes, a procedure for the automatic generation of bifurcation sets, the generalizations of the Mandelbrot set, is implemented. This technique helps greatly in the design of fractal images. A number of application examples proves the usefulness of the approach, and the paper shows that, put into an interactive context, new applications of these fascinating objects become possible. The images presented show that the developed tool can be very useful for artistic work. 1. Introduction an interactive application was not really feasible till the ex- ploitation of the capabilities of new, fast graphics hardware. The developments in the research of dynamical systems and its attractors, chaos and fractals has already led some peo- The development of an interactive fractal visualisation ple to declare that god was a mathematician, because mathe- method, is the main objective of this paper. -

Can Two Chaotic Systems Give Rise to Order? J
Can two chaotic systems give rise to order? 1 2* 3 J. Almeida , D. Peralta-Salas , and M. Romera 1Departamento de Física Teórica I, Facultad de Ciencias Físicas, Universidad Complutense, 28040 Madrid (Spain). 2Departamento de Física Teórica II, Facultad de Ciencias Físicas, Universidad Complutense, 28040 Madrid (Spain). 3Instituto de Física Aplicada, Consejo Superior de Investigaciones Científicas, Serrano 144, 28006 Madrid (Spain). The recently discovered Parrondo’s paradox claims that two losing games can result, under random or periodic alternation of their dynamics, in a winning game: “losing+ losing= winning”. In this paper we follow Parrondo’s philosophy of combining different dynamics and we apply it to the case of one-dimensional quadratic maps. We prove that the periodic mixing of two chaotic dynamics originates an ordered dynamics in certain cases. This provides an explicit example (theoretically and numerically tested) of a different Parrondian paradoxical phenomenon: “chaos + chaos = order”. 1. Introduction One of the most extended ways to model the evolution of a natural process (physical, biological or even economical) is by employing discrete dynamics, that is, maps which apply one point to another point of certain variables space. Deterministic or random laws are allowed, and in this last case the term game is commonly used instead of map (physicists also use the term discrete random process). Let us assume that we have two different discrete dynamics A1 and A2. In the last decades a great effort has been done in understanding at least the most significant qualitative aspects of each dynamics separately. A different (but related) topic of research which has arisen in the last years consists in studying the dynamics obtained by combination of the dynamics A1 and A2: AH 0 AAHH12 xxxx0123¾¾¾®¾¾¾®¾¾¾® .. -
![Arxiv:1808.10408V1 [Math.DS] 30 Aug 2018 Set Md ⊂ C Is Defined As the Set of C Such That the Julia Set J(Fc) Is Con- Nected](https://docslib.b-cdn.net/cover/0024/arxiv-1808-10408v1-math-ds-30-aug-2018-set-md-c-is-de-ned-as-the-set-of-c-such-that-the-julia-set-j-fc-is-con-nected-3160024.webp)
Arxiv:1808.10408V1 [Math.DS] 30 Aug 2018 Set Md ⊂ C Is Defined As the Set of C Such That the Julia Set J(Fc) Is Con- Nected
ON THE INHOMOGENEITY OF THE MANDELBROT SET YUSHENG LUO Abstract. We will show the Mandelbrot set M is locally conformally inhomogeneous: the only conformal map f defined in an open set U intersecting @M and satisfying f(U \ @M) ⊂ @M is the identity map. The proof uses the study of local conformal symmetries of the Julia sets of polynomials: we will show in many cases, the dynamics can be recovered from the local conformal structure of the Julia sets. 1. Introduction Given a monic polynomial f(z), the filled Julia set is n K = K(f) = fz 2 C :(f (z))n2N is boundedg 2 and the Julia set is J = @K. For quadratic family fc(z) = z + c, the Mandelbrot set M can be defined as the subset in the parameter plane such that the Julia set Jc is connected, M = fc 2 C : Jc is connectedg Let A be a compact subset of C. We call an orientation preserving home- omorphism H : U −! V a local conformal symmetry of A if H is conformal, U is connected and H sends U \ A onto V \ A. We say a local conformal symmetry is trivial if it is the identity map or U \ A = ;. In this paper, we will show Theorem 1.1. The boundary of the Mandelbrot set @M admits no non- trivial local conformal symmetries. d Remark 1.2. For a fixed d ≥ 2, and let fc(z) = z + c. The Multibrot arXiv:1808.10408v1 [math.DS] 30 Aug 2018 set Md ⊂ C is defined as the set of c such that the Julia set J(fc) is con- nected. -

Quasisymmetric Conjugacy Between Quadratic Dynamics and Iterated
QUASISYMMETRIC CONJUGACY BETWEEN QUADRATIC DYNAMICS AND ITERATED FUNCTION SYSTEMS KEMAL ILGAR EROGLU,˘ STEFFEN ROHDE, AND BORIS SOLOMYAK Abstract. We consider linear iterated function systems (IFS) with a constant contraction ratio in the plane for which the “overlap set” O is finite, and which are “invertible” on the attractor A, in the sense that there is a continuous surjection q : A → A whose inverse branches are the contractions of the IFS. The overlap set is the critical set in the sense that q is not a local homeomorphism precisely at O. We suppose also that there is a rational function p with the Julia set J such that (A, q) and (J, p) are conjugate. We prove that if A has bounded turning and p has no parabolic cycles, then the conjugacy is quasisymmetric. This result is applied to some specific examples including an uncountable family. Our main focus is on the family of IFS {λz,λz + 1} where λ is a complex parameter in the unit disk, such that its attractor Aλ is a dendrite, which happens whenever O is a singleton. C. Bandt observed that a simple modification of such an IFS (without changing the attractor) is invertible and gives rise to a quadratic-like map qλ on Aλ. If the IFS is post-critically finite, 2 then a result of A. Kameyama shows that there is a quadratic map pc(z)= z + c, with the Julia set Jc such that (Aλ, qλ) and (Jc,pc) are conjugate. We prove that this conjugacy is quasisymmetric and obtain partial results in the general (not post-critically finite) case. -
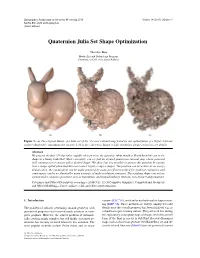
Quaternion Julia Set Shape Optimization
Eurographics Symposium on Geometry Processing 2015 Volume 34 (2015), Number 5 Mirela Ben-Chen and Ligang Liu (Guest Editors) Quaternion Julia Set Shape Optimization Theodore Kim Media Arts and Technology Program University of California, Santa Barbara (a) (b) (c) Figure 1: (a) The original Bunny. (b) Julia set of the 331-root rational map found by our optimization. (c) Highly intricate surface obtained by translating the roots by 1.41 in the z direction. Image is high-resolution; please zoom in to see details. Abstract We present the first 3D algorithm capable of answering the question: what would a Mandelbrot-like set in the shape of a bunny look like? More concretely, can we find an iterated quaternion rational map whose potential field contains an isocontour with a desired shape? We show that it is possible to answer this question by casting it as a shape optimization that discovers novel, highly complex shapes. The problem can be written as an energy minimization, the optimization can be made practical by using an efficient method for gradient evaluation, and convergence can be accelerated by using a variety of multi-resolution strategies. The resulting shapes are not in- variant under common operations such as translation, and instead undergo intricate, non-linear transformations. Categories and Subject Descriptors (according to ACM CCS): I.3.5 [Computer Graphics]: Computational Geometry and Object Modeling—Curve, surface, solid, and object representations 1. Introduction variants [LLC∗10], and similar methods such as hypertextur- ing [EMP∗02]. These methods are widely employed to add The problem of robustly generating smooth geometry with details once the overall geometry has been finalized, e.g. -

Local Connectivity of the Mandelbrot Set at Certain Infinitely Renormalizable Points∗†
Local connectivity of the Mandelbrot set at certain infinitely renormalizable points¤y Yunping Jingz Abstract We construct a subset consisting of infinitely renormalizable points in the Mandelbrot set. We show that Mandelbrot set is locally connected at this subset and for every point in this sub- set, corresponding infinitely renormalizable quadratic Julia set is locally connected. Since the set of Misiurewicz points is in the closure of the subset we construct, therefore, the subset is dense in the boundary of the Mandelbrot set. Contents 1 Introduction, review, and statements of new results 237 1.1 Quadratic polynomials . 237 1.2 Local connectivity for quadratic Julia sets. 240 1.3 Some basic facts about the Mandelbrot set from Douady- Hubbard . 244 1.4 Constructions of three-dimensional partitions. 248 1.5 Statements of new results. 250 2 Basic idea in our construction 252 3 The proof of our main theorem 259 ¤2000 Mathematics Subject Classification. Primary 37F25 and 37F45, Secondary 37E20 yKeywords: infinitely renormalizable point, local connectivity, Yoccoz puzzle, the Mandelbrot set zPartially supported by NSF grants and PSC-CUNY awards and 100 men program of China 236 Complex Dynamics and Related Topics 237 1 Introduction, review, and statements of new results 1.1 Quadratic polynomials Let C and C be the complex plane and the extended complex plane (the Riemann sphere). Suppose f is a holomorphic map from a domain Ω ½ C into itself. A point z in Ω is called a periodic point of period k ¸ 1 if f ±k(z) = z but f ±i(z) 6= z for all 1 · i < k. -

Laplacians on Julia Sets of Rational Maps
LAPLACIANS ON JULIA SETS OF RATIONAL MAPS MALTE S. HASSLER, HUA QIU, AND ROBERT S. STRICHARTZ Abstract. The study of Julia sets gives a new and natural way to look at fractals. When mathematicians investigated the special class of Misiurewicz's rational maps, they found out that there is a Julia set which is homeomorphic to a well known fractal, the Sierpinski gasket. In this paper, we apply the method of Kigami to give rise to a new construction of Laplacians on the Sierpinski gasket like Julia sets with a dynamically invariant property. 1. Introduction Recall that the familiar Sierpinski gasket (SG) is generated in the following way. Starting with a triangle one divides it into four copies, removes the central one, and repeats the iterated process. One aspect of the study of this fractal stems from the analytical construction of a Laplacian developed by Jun Kigami in 1989 [10]. Since then, the analysis on SG has been extensively investigated from various viewpoints. The theory has been extended to some other fractals [11], too. And for some of them one could say they are more invented like SG than discovered. A standard reference to this topic is the book of Robert S. Strichartz [15]. When mathematicians studied the behaviour of polynomial maps under itera- tion, at first, they did not think about fractals. Given a starting point z0 2 C and a polynomial P (z) they wanted to know, whether the sequence of iterations P (z0);P (P (z0))::: converges. They named the set of points that show this behaviour the filled Julia set and its boundary the Julia set after the French mathematician Gaston Julia. -

At the Helm of the Burning Ship
http://dx.doi.org/10.14236/ewic/EVA2019.74 At the Helm of the Burning Ship Claude Heiland-Allen unaffiliated London, UK [email protected] The Burning Ship fractal is a non-analytic variation of the Mandelbrot set, formed by taking absolute values in the recurrence. Iterating its Jacobian can identify the period of attracting orbits; Newton’s root-finding method locates their mini-ships. Size estimates tell how deep to zoom to find the mini-ship or its embedded quasi-Julia set. Pre-periodic Misiurewicz points with repelling dynamics are located by Newton’s method. Stretched regions are automatically unskewed by the Jacobian, which is also good for colouring images using distance estimation. Perturbation techniques cheapen deep zooming. The mathematics can be generalised to other fractal formulas. Some artistic zooming techniques and domain colouring methods are also described. Burning Ship. Dynamical systems. Fractal art. Numerical algorithms. Perturbation theory. 1. IMAGING THE BURNING SHIP 1.1 ESCAPE-TIME FRACTALS Fractals are mathematical objects exhibiting detail at all scales. Escape-time fractals are plotted by iterating recurrence relations parameterised by pixel coordinates from a seed value until the values exceed an escape radius or until an arbitrary limit on iteration count is reached (this is to ensure termination, as some pixels may not escape at all). The colour of each pixel is determined by how quickly the iterates took to escape. Define the integer pixel coordinates by , , with the centre of the image at ,, then the