Varāhamihira and the Poetry of Sines
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Genetic Context for Understanding the Trigonometric Functions Danny Otero Xavier University, [email protected]
Ursinus College Digital Commons @ Ursinus College Transforming Instruction in Undergraduate Pre-calculus and Trigonometry Mathematics via Primary Historical Sources (TRIUMPHS) Spring 3-2017 A Genetic Context for Understanding the Trigonometric Functions Danny Otero Xavier University, [email protected] Follow this and additional works at: https://digitalcommons.ursinus.edu/triumphs_precalc Part of the Curriculum and Instruction Commons, Educational Methods Commons, Higher Education Commons, and the Science and Mathematics Education Commons Click here to let us know how access to this document benefits oy u. Recommended Citation Otero, Danny, "A Genetic Context for Understanding the Trigonometric Functions" (2017). Pre-calculus and Trigonometry. 1. https://digitalcommons.ursinus.edu/triumphs_precalc/1 This Course Materials is brought to you for free and open access by the Transforming Instruction in Undergraduate Mathematics via Primary Historical Sources (TRIUMPHS) at Digital Commons @ Ursinus College. It has been accepted for inclusion in Pre-calculus and Trigonometry by an authorized administrator of Digital Commons @ Ursinus College. For more information, please contact [email protected]. A Genetic Context for Understanding the Trigonometric Functions Daniel E. Otero∗ July 22, 2019 Trigonometry is concerned with the measurements of angles about a central point (or of arcs of circles centered at that point) and quantities, geometrical and otherwise, that depend on the sizes of such angles (or the lengths of the corresponding arcs). It is one of those subjects that has become a standard part of the toolbox of every scientist and applied mathematician. It is the goal of this project to impart to students some of the story of where and how its central ideas first emerged, in an attempt to provide context for a modern study of this mathematical theory. -

International Journal for Scientific Research & Development| Vol. 5, Issue 12, 2018 | ISSN (Online): 2321-0613
IJSRD - International Journal for Scientific Research & Development| Vol. 5, Issue 12, 2018 | ISSN (online): 2321-0613 A Case Study on Applications of Trigonometry in Oceanography Suvitha M.1 Kalaivani M.2 1,2Student 1,2Department of Mathematics 1,2Sri Krishna Arts and Science College, Coimbatore, Tamil Nadu, India Abstract— This article introduces a trigonometric field that bisected to create two right-angle triangles, most problems extends in the field of real numbers adding two elements: sin can be reduced to calculations on right-angle triangles. Thus and cos satisfying an axiom sin²+cos²=1.It is shown that the majority of applications relate to right-angle triangles. assigning meaningful names to particular elements to the One exception to this is spherical trigonometry, the study of field, All know trigonometric identities may be introduced triangles on spheres, surfaces of constant positive curvature, and proved. The main objective of this study is about in elliptic geometry (a fundamental part of astronomy and oceanography how the oceanographers guide everyone with navigation). Trigonometry on surfaces of negative curvature the awareness of the Tsunami waves and protect the marine is part of hyperbolic geometry. animals hitting the ships and cliffs. Key words: Trigonometric Identities, Trigonometric Ratios, II. HISTORY OF TRIGONOMETRY Trigonometric Functions I. INTRODUCTION A. Trigonometry Fig. 2: Hipparchus, credited with compiling the first trigonometric, is known as "the father of trigonometry". A thick ring-like shell object found at the Indus Fig. 1: Valley Civilization site of Lothal, with four slits each in two All of the trigonometric functions of an angle θ can be margins served as a compass to measure angles on plane constructed geometrically in terms of a unit circle centered at surfaces or in the horizon in multiples of 40degrees,upto 360 O. -

Asian Contributions to Mathematics
PORTLAND PUBLIC SCHOOLS GEOCULTURAL BASELINE ESSAY SERIES Asian Contributions to Mathematics By Ramesh Gangolli Ramesh Gangolli Dr. Ramesh Gangolli was born in India, and educated at the University of Bombay, Cambridge University and MIT. He held the Cambridge Society of India Scholarship while at Cambridge University, and was a College Scholar at Peterhouse. During 1966-68 he was a Sloan Foundation Fellow. In 1967, he was awarded the Paul Levy Prize by a Committee of the French Academy of Sciences. At present he is a Professor of Mathematics at the University of Washington, Seattle. He has been active in mathematical research as well as in mathematics education, and has held visiting positions at many universities in the U.S. and abroad. He has served professionally in several capacities: as Chair of the mathematics of the Committee on Education of the American Mathematical Society, and as a member of several committees of the U.S. National Academy of Sciences and the National Research Council. He is also a musician specializing in the Classical Music of India, and is an Adjunct Professor of Music in the School of Music at the University of Washington. Version: 1999-12-22 PPS Geocultural Baseline Essay Series AUTHOR: Gangolli SUBJECT: Math Contents 1. INTRODUCTION. 1 1.1 Purpose of this essay. 1 1.2 Scope. 2 1.3 Acknowledgments. 3 2. SOME VIEWS OF THE DEVELOPMENT OF MATHEMATICS. 5 3. THE PLACE OF MATHEMATICS IN ANCIENT CULTURES. 10 3.1 Agriculture, commerce, etc. 11 3.2 Ritual, worship, etc. 12 3.3 Intellectual curiosity and amusement. -

Construction Surveying Curves
Construction Surveying Curves Three(3) Continuing Education Hours Course #LS1003 Approved Continuing Education for Licensed Professional Engineers EZ-pdh.com Ezekiel Enterprises, LLC 301 Mission Dr. Unit 571 New Smyrna Beach, FL 32170 800-433-1487 [email protected] Construction Surveying Curves Ezekiel Enterprises, LLC Course Description: The Construction Surveying Curves course satisfies three (3) hours of professional development. The course is designed as a distance learning course focused on the process required for a surveyor to establish curves. Objectives: The primary objective of this course is enable the student to understand practical methods to locate points along curves using variety of methods. Grading: Students must achieve a minimum score of 70% on the online quiz to pass this course. The quiz may be taken as many times as necessary to successful pass and complete the course. Ezekiel Enterprises, LLC Section I. Simple Horizontal Curves CURVE POINTS Simple The simple curve is an arc of a circle. It is the most By studying this course the surveyor learns to locate commonly used. The radius of the circle determines points using angles and distances. In construction the “sharpness” or “flatness” of the curve. The larger surveying, the surveyor must often establish the line of the radius, the “flatter” the curve. a curve for road layout or some other construction. The surveyor can establish curves of short radius, Compound usually less than one tape length, by holding one end Surveyors often have to use a compound curve because of the tape at the center of the circle and swinging the of the terrain. -

And Are Congruent Chords, So the Corresponding Arcs RS and ST Are Congruent
9-3 Arcs and Chords ALGEBRA Find the value of x. 3. SOLUTION: 1. In the same circle or in congruent circles, two minor SOLUTION: arcs are congruent if and only if their corresponding Arc ST is a minor arc, so m(arc ST) is equal to the chords are congruent. Since m(arc AB) = m(arc CD) measure of its related central angle or 93. = 127, arc AB arc CD and . and are congruent chords, so the corresponding arcs RS and ST are congruent. m(arc RS) = m(arc ST) and by substitution, x = 93. ANSWER: 93 ANSWER: 3 In , JK = 10 and . Find each measure. Round to the nearest hundredth. 2. SOLUTION: Since HG = 4 and FG = 4, and are 4. congruent chords and the corresponding arcs HG and FG are congruent. SOLUTION: m(arc HG) = m(arc FG) = x Radius is perpendicular to chord . So, by Arc HG, arc GF, and arc FH are adjacent arcs that Theorem 10.3, bisects arc JKL. Therefore, m(arc form the circle, so the sum of their measures is 360. JL) = m(arc LK). By substitution, m(arc JL) = or 67. ANSWER: 67 ANSWER: 70 eSolutions Manual - Powered by Cognero Page 1 9-3 Arcs and Chords 5. PQ ALGEBRA Find the value of x. SOLUTION: Draw radius and create right triangle PJQ. PM = 6 and since all radii of a circle are congruent, PJ = 6. Since the radius is perpendicular to , bisects by Theorem 10.3. So, JQ = (10) or 5. 7. Use the Pythagorean Theorem to find PQ. -

Mathematics in African History and Cultures
Paulus Gerdes & Ahmed Djebbar MATHEMATICS IN AFRICAN HISTORY AND CULTURES: AN ANNOTATED BIBLIOGRAPHY African Mathematical Union Commission on the History of Mathematics in Africa (AMUCHMA) Mathematics in African History and Cultures Second edition, 2007 First edition: African Mathematical Union, Cape Town, South Africa, 2004 ISBN: 978-1-4303-1537-7 Published by Lulu. Copyright © 2007 by Paulus Gerdes & Ahmed Djebbar Authors Paulus Gerdes Research Centre for Mathematics, Culture and Education, C.P. 915, Maputo, Mozambique E-mail: [email protected] Ahmed Djebbar Département de mathématiques, Bt. M 2, Université de Lille 1, 59655 Villeneuve D’Asq Cedex, France E-mail: [email protected], [email protected] Cover design inspired by a pattern on a mat woven in the 19th century by a Yombe woman from the Lower Congo area (Cf. GER-04b, p. 96). 2 Table of contents page Preface by the President of the African 7 Mathematical Union (Prof. Jan Persens) Introduction 9 Introduction to the new edition 14 Bibliography A 15 B 43 C 65 D 77 E 105 F 115 G 121 H 162 I 173 J 179 K 182 L 194 M 207 N 223 O 228 P 234 R 241 S 252 T 274 U 281 V 283 3 Mathematics in African History and Cultures page W 290 Y 296 Z 298 Appendices 1 On mathematicians of African descent / 307 Diaspora 2 Publications by Africans on the History of 313 Mathematics outside Africa (including reviews of these publications) 3 On Time-reckoning and Astronomy in 317 African History and Cultures 4 String figures in Africa 338 5 Examples of other Mathematical Books and 343 -

20. Geometry of the Circle (SC)
20. GEOMETRY OF THE CIRCLE PARTS OF THE CIRCLE Segments When we speak of a circle we may be referring to the plane figure itself or the boundary of the shape, called the circumference. In solving problems involving the circle, we must be familiar with several theorems. In order to understand these theorems, we review the names given to parts of a circle. Diameter and chord The region that is encompassed between an arc and a chord is called a segment. The region between the chord and the minor arc is called the minor segment. The region between the chord and the major arc is called the major segment. If the chord is a diameter, then both segments are equal and are called semi-circles. The straight line joining any two points on the circle is called a chord. Sectors A diameter is a chord that passes through the center of the circle. It is, therefore, the longest possible chord of a circle. In the diagram, O is the center of the circle, AB is a diameter and PQ is also a chord. Arcs The region that is enclosed by any two radii and an arc is called a sector. If the region is bounded by the two radii and a minor arc, then it is called the minor sector. www.faspassmaths.comIf the region is bounded by two radii and the major arc, it is called the major sector. An arc of a circle is the part of the circumference of the circle that is cut off by a chord. -

Ramiz Daniz the Scientist Passed Ahead of Centuries – Nasiraddin Tusi
Ramiz Daniz Ramiz Daniz The scientist passed ahead of centuries – Nasiraddin Tusi Baku -2013 Scientific editor – the Associate Member of ANAS, Professor 1 Ramiz Daniz Eybali Mehraliyev Preface – the Associate Member of ANAS, Professor Ramiz Mammadov Scientific editor – the Associate Member of ANAS, Doctor of physics and mathematics, Academician Eyyub Guliyev Reviewers – the Associate Member of ANAS, Professor Rehim Husseinov, Associate Member of ANAS, Professor Rafig Aliyev, Professor Ajdar Agayev, senior lecturer Vidadi Bashirov Literary editor – the philologist Ganira Amirjanova Computer design – Sevinj Computer operator – Sinay Translator - Hokume Hebibova Ramiz Daniz “The scientist passed ahead of centuries – Nasiraddin Tusi”. “MM-S”, 2013, 297 p İSBN 978-9952-8230-3-5 Writing about the remarkable Azerbaijani scientist Nasiraddin Tusi, who has a great scientific heritage, is very responsible and honorable. Nasiraddin Tusi, who has a very significant place in the world encyclopedia together with well-known phenomenal scientists, is one of the most honorary personalities of our nation. It may be named precious stone of the Academy of Sciences in the East. Nasiraddin Tusi has masterpieces about mathematics, geometry, astronomy, geography and ethics and he is an inventor of a lot of unique inventions and discoveries. According to the scientist, America had been discovered hundreds of years ago. Unfortunately, most peoples don’t know this fact. I want to inform readers about Tusi’s achievements by means of this work. D 4702060103 © R.Daniz 2013 M 087-2013 2 Ramiz Daniz I’m grateful to leaders of the State Oil Company of Azerbaijan Republic for their material and moral supports for publication of the work The book has been published in accordance with the order of the “Partner” Science Development Support Social Union with the grant of the State Oil Company of Azerbaijan Republic Courageous step towards the great purpose 3 Ramiz Daniz I’m editing new work of the young writer. -

From the Theorem of the Broken Chord to the Beginning of the Trigonometry
From the Theorem of the Broken Chord to the Beginning of the Trigonometry MARIA DRAKAKI Advisor Professor:Michael Lambrou Department of Mathematics and Applied Mathematics University of Crete May 2020 1/18 MARIA DRAKAKI From the Theorem of the Broken Chord to the Beginning of the TrigonometryMay 2020 1 / 18 Introduction. Τhe Theorem Some proofs of it Archimedes and Trigonometry The trigonometric significance of the Theorem of the Broken Chord The sine of half of the angle Is Archimedes the founder of Trigonometry? ”Who is the founder of Trigonometry?” an open question Conclusion Contents The Broken Chord Theorem 2/18 MARIA DRAKAKI From the Theorem of the Broken Chord to the Beginning of the TrigonometryMay 2020 2 / 18 Archimedes and Trigonometry The trigonometric significance of the Theorem of the Broken Chord The sine of half of the angle Is Archimedes the founder of Trigonometry? ”Who is the founder of Trigonometry?” an open question Conclusion Contents The Broken Chord Theorem Introduction. Τhe Theorem Some proofs of it 2/18 MARIA DRAKAKI From the Theorem of the Broken Chord to the Beginning of the TrigonometryMay 2020 2 / 18 The trigonometric significance of the Theorem of the Broken Chord The sine of half of the angle Is Archimedes the founder of Trigonometry? ”Who is the founder of Trigonometry?” an open question Conclusion Contents The Broken Chord Theorem Introduction. Τhe Theorem Some proofs of it Archimedes and Trigonometry 2/18 MARIA DRAKAKI From the Theorem of the Broken Chord to the Beginning of the TrigonometryMay 2020 2 / 18 Is Archimedes the founder of Trigonometry? ”Who is the founder of Trigonometry?” an open question Conclusion Contents The Broken Chord Theorem Introduction. -
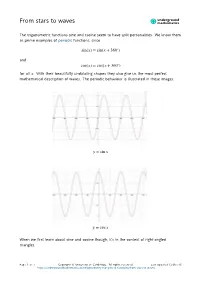
From Stars to Waves Mathematics
underground From stars to waves mathematics The trigonometric functions sine and cosine seem to have split personalities. We know them as prime examples of periodic functions, since sin(푥) = sin(푥 + 360∘) and cos(푥) = cos(푥 + 360∘) for all 푥. With their beautifully undulating shapes they also give us the most perfect mathematical description of waves. The periodic behaviour is illustrated in these images. 푦 = sin 푥 푦 = cos 푥 When we first learn about sine and cosine though, it’s in the context of right-angled triangles. Page 1 of 7 Copyright © University of Cambridge. All rights reserved. Last updated 12-Dec-16 https://undergroundmathematics.org/trigonometry-triangles-to-functions/from-stars-to-waves How do the two representations of these two functions fit together? Imagine looking up at the night sky and try to visualise the stars and planets all lying on a sphere that curves around us, with the Earth at its centre. This is called a celestial sphere. Around 2000 years ago, when early astronomers were trying to chart the night sky, doing astronomy meant doing geometry involving spheres—and that meant being able to do geometry involving circles. Looking at two stars on the celestial sphere, we can ask how far apart they are. We can formulate this as a problem about points on a circle. Given two points 퐴 and 퐵 on a cirle, what is the shortest distance between them, measured along the straight line that lies inside the circle? Such a straight line is called a chord of the circle. Page 2 of 7 Copyright © University of Cambridge. -

Lesson 2: Circles, Chords, Diameters, and Their Relationships
NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 2 M5 GEOMETRY Lesson 2: Circles, Chords, Diameters, and Their Relationships Student Outcomes . Identify the relationships between the diameters of a circle and other chords of the circle. Lesson Notes Students are asked to construct the perpendicular bisector of a line segment and draw conclusions about points on that bisector and the endpoints of the segment. They relate the construction to the theorem stating that any perpendicular bisector of a chord must pass through the center of the circle. Classwork Opening Exercise (4 minutes) Scaffolding: Post a diagram and display the steps to create a Opening Exercise perpendicular bisector used in Construct the perpendicular bisector of line segment below (as you did in Module 1). Lesson 4 of Module 1. ���� Label the endpoints of the segment and . Draw circle with center and radius . Draw another line that bisects but is not perpendicular to it. Draw circle with center ���� and radius . List one similarity and one difference���� between the two bisectors. . Label the points of Answers will vary. All points on the perpendicular bisector are equidistant from points and 46T . ���� Points on the other bisector are not equidistant from points A and B. The perpendicular bisector intersection as and . meets at right angles. The other bisector meets at angles that are not congruent. Draw . ���� ⃖����⃗ You may wish to recall for students the definition of equidistant: EQUIDISTANT:. A point is said to be equidistant from two different points and if = . Points and can be replaced in the definition above with other figures (lines, etc.) as long as the distance to those figures is given meaning first. -

11.4 Arcs and Chords
Page 1 of 5 11.4 Arcs and Chords Goal By finding the perpendicular bisectors of two Use properties of chords of chords, an archaeologist can recreate a whole circles. plate from just one piece. This approach relies on Theorem 11.5, and is Key Words shown in Example 2. • congruent arcs p. 602 • perpendicular bisector p. 274 THEOREM 11.4 B Words If a diameter of a circle is perpendicular to a chord, then the diameter bisects the F chord and its arc. E G Symbols If BG&* ∏ FD&* , then DE&* c EF&* and DGs c GFs. D EXAMPLE 1 Find the Length of a Chord In ᭪C the diameter AF&* is perpendicular to BD&* . D Use the diagram to find the length of BD&* . 5 F C Solution E A Because AF&* is a diameter that is perpendicular to BD&* , you can use Theorem 11.4 to conclude that AF&* bisects B BD&* . So, BE ϭ ED ϭ 5. BD ϭ BE ϩ ED Segment Addition Postulate ϭ 5 ϩ 5 Substitute 5 for BE and ED . ϭ 10 Simplify. ANSWER ᮣ The length of BD&* is 10. Find the Length of a Segment 1. Find the length of JM&* . 2. Find the length of SR&* . H P 12 K C S C M N G 15 P J R 608 Chapter 11 Circles Page 2 of 5 THEOREM 11.5 Words If one chord is a perpendicular bisector M of another chord, then the first chord is a diameter. J P K Symbols If JK&* ∏ ML&* and MP&** c PL&* , then JK&* is a diameter.