Wireless Engineer
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
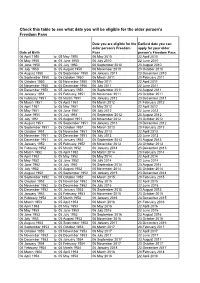
Copy of Age Eligibility from 6 April 10
Check this table to see what date you will be eligible for the older person's Freedom Pass Date you are eligible for the Earliest date you can older person's Freedom apply for your older Date of Birth Pass person's Freedom Pass 06 April 1950 to 05 May 1950 06 May 2010 22 April 2010 06 May 1950 to 05 June 1950 06 July 2010 22 June 2010 06 June 1950 to 05 July 1950 06 September 2010 23 August 2010 06 July 1950 to 05 August 1950 06 November 2010 23 October 2010 06 August 1950 to 05 September 1950 06 January 2011 23 December 2010 06 September 1950 to 05 October 1950 06 March 2011 20 February 2011 06 October 1950 to 05 November 1950 06 May 2011 22 April 2011 06 November 1950 to 05 December 1950 06 July 2011 22 June 2011 06 December 1950 to 05 January 1951 06 September 2011 23 August 2011 06 January 1951 to 05 February 1951 06 November 2011 23 October 2011 06 February 1951 to 05 March 1951 06 January 2012 23 December 2011 06 March 1951 to 05 April 1951 06 March 2012 21 February 2012 06 April 1951 to 05 May 1951 06 May 2012 22 April 2012 06 May 1951 to 05 June 1951 06 July 2012 22 June 2012 06 June 1951 to 05 July 1951 06 September 2012 23 August 2012 06 July 1951 to 05 August 1951 06 November 2012 23 October 2012 06 August 1951 to 05 September 1951 06 January 2013 23 December 2012 06 September 1951 to 05 October 1951 06 March 2013 20 February 2013 06 October 1951 to 05 November 1951 06 May 2013 22 April 2013 06 November 1951 to 05 December 1951 06 July 2013 22 June 2013 06 December 1951 to 05 January 1952 06 September 2013 23 August 2013 06 -

Country Term # of Terms Total Years on the Council Presidencies # Of
Country Term # of Total Presidencies # of terms years on Presidencies the Council Elected Members Algeria 3 6 4 2004 - 2005 December 2004 1 1988 - 1989 May 1988, August 1989 2 1968 - 1969 July 1968 1 Angola 2 4 2 2015 – 2016 March 2016 1 2003 - 2004 November 2003 1 Argentina 9 18 15 2013 - 2014 August 2013, October 2014 2 2005 - 2006 January 2005, March 2006 2 1999 - 2000 February 2000 1 1994 - 1995 January 1995 1 1987 - 1988 March 1987, June 1988 2 1971 - 1972 March 1971, July 1972 2 1966 - 1967 January 1967 1 1959 - 1960 May 1959, April 1960 2 1948 - 1949 November 1948, November 1949 2 Australia 5 10 10 2013 - 2014 September 2013, November 2014 2 1985 - 1986 November 1985 1 1973 - 1974 October 1973, December 1974 2 1956 - 1957 June 1956, June 1957 2 1946 - 1947 February 1946, January 1947, December 1947 3 Austria 3 6 4 2009 - 2010 November 2009 1 1991 - 1992 March 1991, May 1992 2 1973 - 1974 November 1973 1 Azerbaijan 1 2 2 2012 - 2013 May 2012, October 2013 2 Bahrain 1 2 1 1998 - 1999 December 1998 1 Bangladesh 2 4 3 2000 - 2001 March 2000, June 2001 2 Country Term # of Total Presidencies # of terms years on Presidencies the Council 1979 - 1980 October 1979 1 Belarus1 1 2 1 1974 - 1975 January 1975 1 Belgium 5 10 11 2007 - 2008 June 2007, August 2008 2 1991 - 1992 April 1991, June 1992 2 1971 - 1972 April 1971, August 1972 2 1955 - 1956 July 1955, July 1956 2 1947 - 1948 February 1947, January 1948, December 1948 3 Benin 2 4 3 2004 - 2005 February 2005 1 1976 - 1977 March 1976, May 1977 2 Bolivia 3 6 7 2017 - 2018 June 2017, October -

NJDARM: Collection Guide
NJDARM: Collection Guide - NEW JERSEY STATE ARCHIVES COLLECTION GUIDE Record Group: Department of Institutions and Agencies Series: Welfare Reporter [incomplete], 1946-1957 Accession #: 1985.011, 1998.097 and unknown Series #: SIN00002 Guide Date: 4/1996 (JK); rev. 2/1999 (EC) Volume: 1.0 c.f. [2 boxes] Contents Content Note This series consists of an incomplete run of the Department of Institutions and Agencies' monthly publication, the Welfare Reporter. Articles in this publication discuss the various aspects of health, welfare and penology. Included are profiles of administrators and employees, stories on specific institutions, and discussions of trends in the care and treatment of those entrusted to the Department of Institutions and Agencies. NOTE: The New Jersey State Library holds a complete run of the Welfare Reporter from May 1946 to January 1972, when it ceased to be published. It is not clear why "interim" issues were published between 1952 and 1955. Interim Issue 27 (April 1955) includes a subject and name index for all of the interim issues (copy attached). Contents Box 1 Volume I, Number 2, June 1946 [1 copy]. Volume III, Number 2, June 1948 [1 copy]. Volume IV, Number 9, January 1950 [3 copies]. Volume IV, Number 10, February 1950 [3 copies]. Volume IV, Number 11, March 1950 [3 copies]. Volume IV, Number 12, April 1950 [3 copies]. Volume V, Number 1, May 1950 [3 copies]. Volume V, Number 2, June 1950 [3 copies]. Volume V, Number 9, January 1951 [3 copies]. Volume V, Number 10, February 1951 [3 copies]. Volume V, Number 11, March 1951 [3 copies]. -

23 February 1955 SWEDISH ANTI-DUMPING DUTIES Report
23 February 1955 SWEDISH ANTI-DUMPING DUTIES Report adopted on 26 February L/328 - 3S/81 INTRODUCTION 1. The Panel on Complaints examined with the representatives of Italy and Sweden the complaint of the Italian Government that the Swedish anti-dumping regulations were not consistent with the obligations of Sweden under the General Agreement and that the administration of these regulations impaired the benefits which should accrue to Italy under that Agreement1. The Panel heard statements from the two parties and obtained from them additional information to clarify a number of points. On the basis of that documentation, the Panel considered if and to what extent the Swedish Royal Decree of 15 October 1954 regarding the levying of anti-dumping duties with respect to the importation of ladies stockings of nylon or similar synthetic fibres was consistent with the provisions of the General Agreement. It considered further whether and to what extent the administration of that decree had actually impaired the benefits accruing directly or indirectly to the Government of Italy under General Agreement. Finally, the panel agreed on the text of a recommendation which, in its opinion, would best assist the Italian and Swedish Governments in arriving at a satisfactory adjustment of the question submitted by Italy to the CONTRACTING PARTIES. FACTS OF THE CASE 2. On 29 May 1954, the Swedish Government introduced anti-dumping duties on the importation of nylon stockings. In accordance with this Decree, an anti-dumping duty was levied whenever the invoice price was lower than the relevant minimum price fixed by the Swedish Government, the importer being entitled to obtain a refund of that duty if the case of dumping was not established. -

SNOW SURVEY of GREAT BRITAIN Season 1955-56 the Basic Material
Reprinted from the METEOROLOGICAL MAGAZINE Vol. 85,1956, PP- 353-361 SNOW SURVEY OF GREAT BRITAIN Season 1955-56 The basic material for this report has been obtained, as in previous years, from returns made by voluntary observers who have provided, month by month, daily records of snowfall and of any snow cover in sight. These records, from a network of stations distributed over the country, are augmented by data extracted from the regular monthly returns from official weather stations and from voluntary climatological stations reporting to the Meteorological Office. Without the co-operation of all those responsible for these voluntary observa- tions, this report could not have been prepared in anything like its present detail. The measurements of snow depth are given in inches and refer in general to 0900 G.M. T. or thereabouts. Summary of 1955-56 season. -Snowfall was about average, taking the season as a whole, and occurred mainly during January and February. There was little snow in November or after March except in Scotland. During January snow was most frequent in Scotland, but in February it was almost as frequent in the Midlands and eastern England as further north. Figs. r and 2 show the number of days of snow falling and snow lying respectively during the season and are based on observations from some 450 stations. Snow fell on more than 7o days in the Grampians, 50 over the high ground in the Southern Uplands, 40 in the Pennines and 30 over most of the country north of a line roughly from Aberystwyth, Cardiganshire, to Felixstowe, Suffolk, except western coastal districts, areas around the Humber basin and a broad belt across the country from the Firth of Clyde to the Firth of Forth. -

EMERGENCY PREPAREDNESS, OFFICE OF: Printed Material, 1953-61
DWIGHT D. EISENHOWER LIBRARY ABILENE, KANSAS EMERGENCY PREPAREDNESS, OFFICE OF: Printed Material, 1953-61 Accession A75-26 Processed by: TB Date Completed: December 1991 This collection was received from the Office of Emergency Preparedness, via the National Archives, in March 1975. No restrictions were placed on the material. Linear feet of shelf space occupied: 5.2 Approximate number of pages: 10,400 Approximate number of items: 6,000 SCOPE AND CONTENT NOTE This collection consists of printed material that was collected for reference purposes by the staff of the Office of Defense Mobilization (ODM) and the Office of Civil and Defense Mobilization (OCDM). The material was inherited by the Office of Emergency Preparedness (OEP), a successor agency to ODM and OCDM. After the OEP was abolished in 1973 the material was turned over to the National Archives and was then sent to the Eisenhower Library. The printed material consists mostly of press releases and public reports that were issued by the White House during the Eisenhower administration. These items are arranged in chronological order by date of release. Additional sets of the press releases are in the Kevin McCann records and in the records of the White House Office, Office of the Press Secretary. Copies of the reports are also in the White House Central Files. The collection also contained several books, periodicals and Congressional committee prints. These items have been transferred to the Eisenhower Library book collection. CONTAINER LIST Box No. Contents 1 Items Transferred -

Annual Report and Accounts 1956
BANK OF ENGLAND REPORT FOR THE YEAR ENDED 29th FEBRUARY 1956 Issued by Order 0/ the Court of Directors. 19th Jllly. 1956. COURT OF DIRECTORS FOR THE YEAR ENDED 29TH FEBRUARY, 1956. CAMERDN FROMANTEEt. COBBOlD, ESQ., GOVERNOR. HUMPHREY CHARLES B.~SKER V! LLE MYNQRS. EsQ., DEPUTY GOVERNOR. SIR GWRGE EOMOND BRACK.ENBURY ABELL, K.C.l.E" O.B.E. THE RT. HON. LoRD BICESTER. SIR GEaRGE LEwlS FRENCH BOLTON, K.C.M.O. LAURENCE J OHN C"DBURY, ESQ., 0.8.£. GEOFFREY CEelL R VVES ELBY, EsQ., C.B.E. SIR CHARLES JOCELYN H AMBRO. lCD.E .. M.C. S IR JOHN COLDBROOK HANBURy-WILLlAMS, C.V.O. FRANK CVRIL H "WKER. EsQ. WllllAM J OHNSTON KESWiCK, EsQ. THE! RT. HON. LORD K 1NDERSLEY, C.B.E .. M.C. SIR ANOREW NAESMITH. C.B.E., J.P. SIR KENNETH OSWALD PEPPIATI. K.B.£., M.C. THE RT. H ON. LORD PIERey, C.D.E. SIR W!LLlAM HENRY P1LK1NGTON. BASIL SANDF-RSON, EsQ .. M.C. MICHAEL J AMES BABINGTON SMITH, E SQ., C.B.E. BANK OF ENGLAND R eport for the year ended 29th February, 1956 Note Circulation and Issue Department The totals of Notes Issued and Paid in recent years are shown in the following table:- I millions NOTES ISSUED, P AID AND IN CIRCULATION YeAR TO END OF FEBRUARY 1952 1953 1954 1955 1956 Issued during the year 1,095 1,136 ),144 1.231 1.354 Paid during the year 1.015 1,Q35 1.064 1,116 1,231 In circulation at end of tbe year .. -
No. 4 February 1955
VOL. L NO. 4 FEBRUARY 955 What New Benefits? Fels Grant To Study One of the most widely discussed subjects among Faculty Conditions faculty and staff groups-and certainly the one which was the most provocative subject of the University Senate The University of Pennsylvania has received a grant meeting held in Dietrich Hall on February 24th-is "What of $25,000 from the Fels Fund to study policies and additional faculty benefits will be realized as a result of practices which contribute most effectively to the develop- the tuition increases which will take place next July 1st, ment of the strongest possible faculty working under the and as a result of additional State aid, if such aid is best possible conditions. forthcoming?" The study, looking toward the development of an affirmative for will be made Tuition increases, if enrollment holds up to present policy faculty personnel, by a committee of the of which Dr. David figures, will result in approximately one million dollars University faculty R. Goddard, Professor of will serve as the chair- above last year's funds. About half of this must be applied Botany, man. Others on the committee are Doctors John A. Goff, to the anticipated 1955-56 operating deficit University's Clarence A. Clarence Morris, Glenn R. Morrow, costs including faculty salaries Kulp, representing University and P. The of the which have been assumed prior to the availability of Eugene Pendergrass. responsibility committee will involve both the initiation and conduct of funds to meet them. The remaining funds will be divided its and the recommendation of between faculty benefits, maintenance, and a small amount investigations policies. -
Publications from Niagara Area Companies
Publications from Niagara area Companies The Tapping Pot, the Electro Metallurgical Company, Unit of Union Carbide and Carbon Corporation Issues: Vol. 18, No. 7---July, 1948 Cooperation, Kimberly-Clark Corporation Issues: March-April 1940 May-June 1942 March-April 1944 May-June 1944 The Lowdown, Lake Ontario Ordnance Works Issues: Volume 1, No. 3-- November, 1942 The Carbo-Wheel, The Employees’ News-Magazine of the Carborundum Company, Niagara Falls, N.Y. Vol. 2, No. 9—September, 1944 (only cover) Vol. 2, No. 12—December, 1944 Vol.3, No. 1—January, 1945 Vol. 3, No.2—February, 1945 (2 copies) Vol. 3, No. 3—March, 1945 Vol. 3, No. 11—December, 1945 Vol. 4, No. 2—February, 1946 Vol. 4, No. 3—March, 1946 Vol. 4, No. 4—April, 1946 Vol. 4, No.7—August, 1946 Vol. 4, No. 8—September, 1946 Vol. 4, No. 9—October, 1946 Vol. 4, No. 10—November, 1946 Vol. 4, No. 11—December, 1946 Vol. 5, No. 1---January, 1947 Vol. 5, No. 2—February, 1947 Vol. 5, No.3—March, 1947 Vol. 5, No. 4—April, 1947 Vol. 5, No. 5—May, 1947 Vol. 5, No. 6—June, 1947 Vol. 5, No. 8—August, 1947 Vol. 5, No. 9—September, 1947 Vol. 5, No. 10—October, 1947 Vol. 5, No. 11—November, 1947 Vol. 5, No. 12—December, 1947 Vol. 6, No. 1—January, 1948 Vol. 6, No. 2—February, 1948 Vol. 6, No. 3—March, 1948 Vol. 6, No. 4—April, 1948 Vol. 6, No. 7—July, 1948 Vol. 6, No. 8—August, 1948 Vol. -
Special Collections and University Archives Roy E. Furman Papers
Special Collections and University Archives Roy E. Furman Papers Manuscript Group 59 For Scholarly Use Only Last Modified October 8, 2014 Indiana University of Pennsylvania 302 Stapleton Library Indiana, PA 15705-1096 Voice: (724) 357-3039 Fax: (724) 357-4891 Manuscript Group 59 2 Roy E. Furman Papers, Manuscript Group 59 Indiana University of Pennsylvania, Special Collections and University Archives 14 boxes; 14 linear feet Biographical Note Roy E. Furman (April 16, 1901-May 18, 1977) was a native of Davidson, Greene County, Pennsylvania. He was elected as a Democrat representing Greene County to the Pennsylvania House of Representatives in 1933 and served four terms until November 30, 1940. He was the 129th Speaker of the Pennsylvania House of Representatives from March 14, 1936-November 30, 1938 under Governor George Howard Earle (1890-1974). Roy Furman served as Lieutenant Governor of Pennsylvania from January 1955-1959 under Governor Michael Leader (1918-2013). In 1959, Furman ran for the Democratic nomination for Pennsylvania Governor, but he was defeated by David Lawrence, who later appointed Furman to the Pennsylvania Turnpike Commission. Roy Furman retired to New Cumberland, Cumberland County, Pennsylvania. Scope and Contents The Roy E. Furman papers are housed in 14 archival boxes. This collection contains the papers of Pennsylvania Lt. Governor Furman during the term in office (January 1955-January 1959). The collection is grouped into four series: correspondence, speeches, campaign 1958, and Board of Pardons. This collection is important for its detailed content of the duties and responsibilities of a Lt. Governor, from the everyday correspondence with local officials and citizens to the more detailed work of the Board of Pardons. -

Download FEBRUARY 1958.Pdf
0' 1958 Federal Bureau of Investigation FEBRUARY United States Department of Justice Vol. 27 No.2 J. Edgar Hoover, Director FBI Law Enforcement Bulletin Restricted to the Use of Law Enforcement Officials FEBRUARY 1958 Vol. 27, No.2 CONTENTS Page The FBI Law En- Statement of Director J. Edgar Hoover. .. 1 forcement Bulletin Feature Article: is issued monthly to lawcnforccment Police Duties and Operations on Ohio Turnpike, by Lt. John 1. Bishop, Commanding Officer, Ohio Turnpike Patrol, Ohio State Highway agencies through- Patrol . 3 ou t the Unitcd States. Much of FacUities: thc data appearing ' New Headquarters Building Aids Police Work, by Chief James J. hcrein is of such a Salerno, Port Washington, N. Y., Police Department . .. 9 nature that its cir- Firearms Training: culation should be Training Courses in Double Action Police Shooting 12 limited to lawcn- Firearms Training Pays Dividend . 17 forcemcn t officers; therefore, material Police Units: contained in this Sheriff's Mounted Posse Increases Police Strength, by Glenn T. Job, Bullelin may not Benton Harbor, Mich.," ews Palladium" . 18 be reprinted with- Identification: out prior authori- Interesting Pattern. back cover zation by lhe Federal Bureau of Other Topics: Investigation. Rebuilding a Small Department for More Efficiency, by Chief Floyd E. Davis, Bennettsville, S. c., Police Department 21 Traffic Engineering Courses 11 ~ Fraudulent Securities. 23 I Wanted by the FBI . 24 Uniform Crime Reporting Change Announced inside back cover Published by the FEDERAL BUREAU OF INVESTIGATION, UNITED STATES DEPARTMENT OF JUSTICE, Washington 25, D. C. 1 - Dnffell itates 1B.epurtm.ent of I1ustir.e 1H.ell.eral fSur.euu of Jlnu.estigatinn llJusqington 25, it Qt. -

OCB Central Files Series
WHITE HOUSE OFFICE, NATIONAL SECURITY COUNCIL STAFF: Papers, 1948-61 Operations Coordinating Board (OCB) Central File Series CONTAINER LIST Box No. Contents 1 OCB 000.1 [Politics] [1956-1957] [Legal status of the Communist Party outside of the Soviet Bloc] OCB 000.1 USSR (File #1) (1)-(7) [November 1953 - June 1956] [Working Group on Stalinism and Special Committee Soviet and Related Problems] OCB 000.1 USSR (File #2) (1)-(6) [July 1956 - June 1957] [Special Committee on Soviet and Related Problems] 2 OCB 000.3 [Religion] (File #1) (1)-(7) [February 1954 - January 1957] [World Council of Churches; Russian Orthodox Church; Ideological Working Group; Buddhism] OCB 000.3 [Religion] (File #2) (1)-(4) [January - May 1957] [Islam; Buddhism] OCB 000.7 [Publicity and Public Press] [June 1953 - February 1956] [Chemical munitions; International Geophysical Year; Communist activities in the Press] OCB 000.75 [Press Clippings] [1954] OCB 000.76 [Newspapers and Magazines] [1954-1956] OCB 000.77 [Radio Broadcasts] (File #1) (1) (2) [October - December 1953] [Working Group on U.S. International Broadcasting; Technical Panel on International Broadcasting (TPIB)] 3 OCB 000.77 [Radio Broadcasts] (File #1) (3)-(10) [December 1953 - June 1954] [Technical Panel on International Broadcasting; Voice of America; electro-magnetic communications and effectiveness of International Broadcasting (NSC 169); country papers for 169 study] OCB 000.77 [Radio Broadcasts] (File #2) (1)-(8) [June - August 1954] [country papers for 169 study] 4 OCB 000.77 [Radio Broadcasts] (File #3) (1)-(13) [August - November 1954] [country papers for 169 study] OCB 000.77 [Radio Broadcasts] (File #4) (1)-(4) [September - November 1954] [effectiveness of U.S.