DOCSLIB.ORG

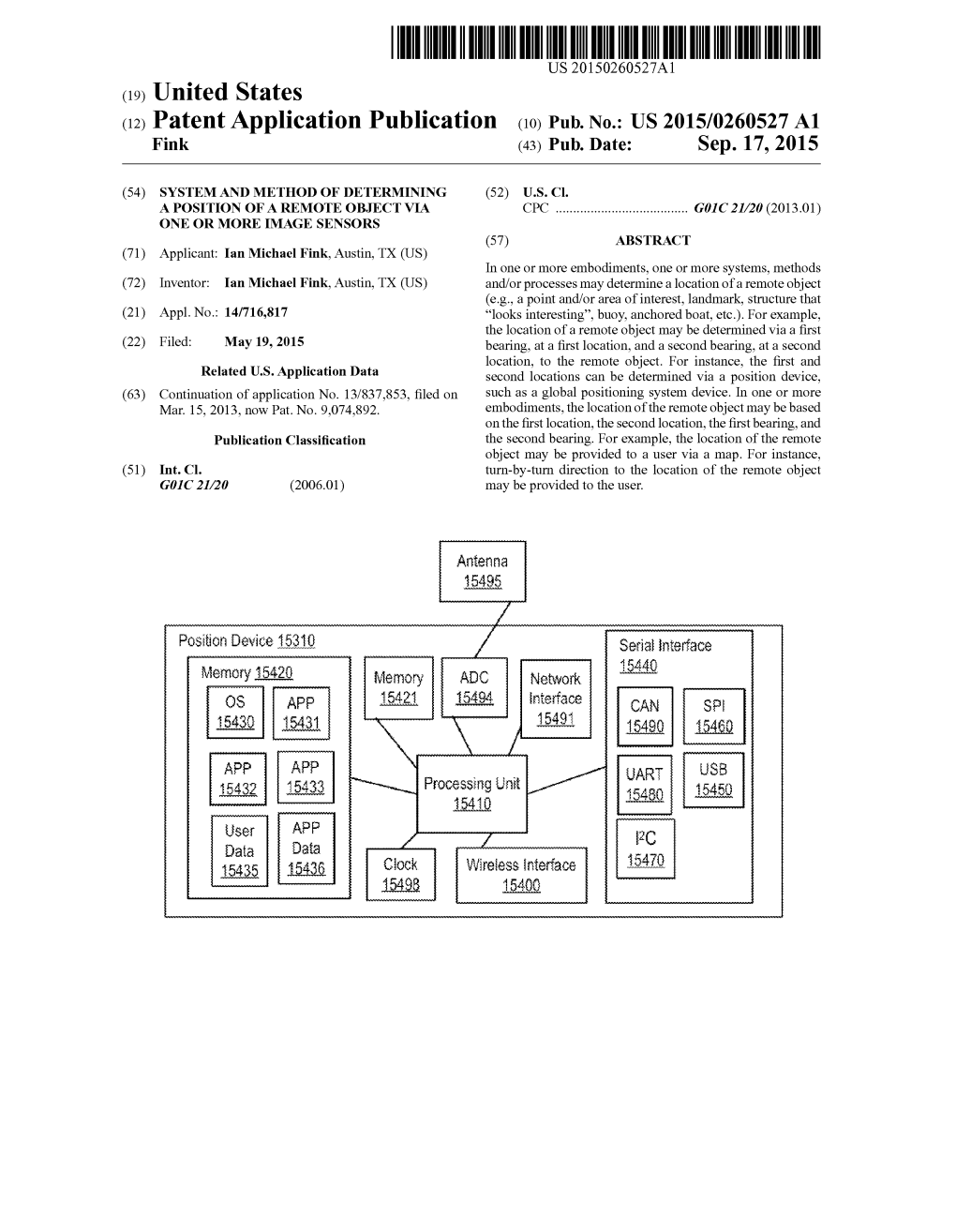
(12) Patent Application Publication (10) Pub. No.: US 2015/0260527 A1 Fink (43) Pub

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
(12) Patent Application Publication (10) Pub. No.: US 2015/0260527 A1 Fink (43) Pub US 20150260527A1 (19) United States (12) Patent Application Publication (10) Pub. No.: US 2015/0260527 A1 Fink (43) Pub. Date: Sep. 17, 2015 (54) SYSTEMAND METHOD OF DETERMINING (52) U.S. Cl. A POSITION OF A REMOTE OBJECT VA CPC ...................................... G0IC 2 1/20 (2013.01) ONE ORMORE IMAGE SENSORS (57) ABSTRACT (71) Applicant: Ian Michael Fink, Austin, TX (US) In one or more embodiments, one or more systems, methods (72) Inventor: Ian Michael Fink, Austin, TX (US) and/or processes may determine a location of a remote object (e.g., a point and/or area of interest, landmark, structure that (21) Appl. No.: 14/716,817 “looks interesting, buoy, anchored boat, etc.). For example, the location of a remote object may be determined via a first (22) Filed: May 19, 2015 bearing, at a first location, and a second bearing, at a second O O location, to the remote object. For instance, the first and Related U.S. Application Data second locations can be determined via a position device, (63) Continuation of application No. 13/837,853, filed on Such as a global positioning system device. In one or more Mar. 15, 2013, now Pat. No. 9,074,892. embodiments, the location of the remote object may be based on the first location, the second location, the first bearing, and Publication Classification the second bearing. For example, the location of the remote object may be provided to a user via a map. For instance, (51) Int. Cl. turn-by-turn direction to the location of the remote object GOIC 2L/20 (2006.01) may be provided to the user. Seria interface 54: iviemory Network 52 le59. 1549CAN Processing it AR 341 543 Wireless interface 347 5. Patent Application Publication Sep. 17, 2015 Sheet 1 of 63 US 2015/0260527 A1 Patent Application Publication Sep. 17, 2015 Sheet 2 of 63 US 2015/0260527 A1 s S S S S -3. - - s & Š & & S S s s a axu Y-SS Patent Application Publication Sep. 17, 2015 Sheet 3 of 63 US 2015/0260527 A1 2. FG. 2 (Prior Art) Patent Application Publication Sep. 17, 2015 Sheet 4 of 63 US 2015/0260527 A1 Patent Application Publication Sep. 17, 2015 Sheet 5 of 63 US 2015/0260527 A1 o ress ser s S& Patent Application Publication Sep. 17, 2015 Sheet 6 of 63 US 2015/0260527 A1 --------- 541C S 3. F.G. 5A Patent Application Publication Sep. 17, 2015 Sheet 7 of 63 US 2015/0260527 A1 50 ra F.G. 5B Patent Application Publication Sep. 17, 2015 Sheet 8 of 63 US 2015/0260527 A1 6.30 3. 6. 83. F.G. 6A Patent Application Publication Sep. 17, 2015 Sheet 9 of 63 US 2015/0260527 A1 805 34. 800 83) F.G. 6B Patent Application Publication Sep. 17, 2015 Sheet 10 of 63 US 2015/0260527 A1 SO 34 8): 83 F.G. 6C Patent Application Publication Sep. 17, 2015 Sheet 11 of 63 US 2015/0260527 A1 87) | s F.G. 6D Patent Application Publication Sep. 17, 2015 Sheet 12 of 63 US 2015/0260527 A1 SOGG 63 FIG. 6E Patent Application Publication Sep. 17, 2015 Sheet 13 of 63 US 2015/0260527 A1 S. 8. 8:30 F.G. 6F Patent Application Publication Sep. 17, 2015 Sheet 14 of 63 US 2015/0260527 A1 554, 8 630 F.G. 6G Patent Application Publication Sep. 17, 2015 Sheet 15 of 63 US 2015/0260527 A1 K --- sees were c n D in ser r s res f s t s w Y e ex$8ws Patent Application Publication Sep. 17, 2015 Sheet 16 of 63 US 2015/0260527 A1 g Patent Application Publication Sep. 17, 2015 Sheet 17 of 63 US 2015/0260527 A1 FG, 9A Patent Application Publication Sep. 17, 2015 Sheet 18 of 63 US 2015/0260527 A1 905 s 8: 830 FIG. 9B Patent Application Publication Sep. 17, 2015 Sheet 19 of 63 US 2015/0260527 A1 74 387 6: 63 F.G. 9C Patent Application Publication Sep. 17, 2015 Sheet 20 of 63 US 2015/0260527 A1 83,80 Patent Application Publication Sep. 17, 2015 Sheet 21 of 63 US 2015/0260527 A1 ************************** Patent Application Publication Sep. 17, 2015 Sheet 22 of 63 US 2015/0260527 A1 39489Œ Patent Application Publication Sep. 17, 2015 Sheet 23 of 63 US 2015/0260527 A1 8vice ( Network Network Memory 332 interface interface fiemory 39 303 WireeSS OS APP 1302 terface 33 303 3. AP APP Wireless 3O32 333 interface Processor 300 Usef Data 3035 Patent Application Publication Sep. 17, 2015 Sheet 24 of 63 US 2015/0260527 A1 Device vestory iO2 Memory Network inefaceifeless OS APP 14021 140go 4. 43 i33 Weess interface Processing Unit 4}{ AR 3. Memory 52 Device C2 OS APP interface 53 33 59 GPO :54, ARP APP 532 5:33 Nieless inteface APP Processing rit ata 5. 50 338 S&ria interface 520 Position UART | UART || |2C 2C spy SP USB use Device 58 38 5 570 58 560 53 15:50 8 530 F.G. 15 Patent Application Publication Sep. 17, 2015 Sheet 25 of 63 US 2015/0260527 A1 Memory 32 Memory Network OS APP 82 terface GPO 603 SO3. 3. 8): APP APP 18032 16033 Wireless As Processing init interface Data 60 8:0 8038 Seis interface 16210 AR Air 2C C 168 168 67 807 Memory 17.2 CS AP 73 3. A P reless intefface AigiQ int Device 737, F.G. 17 Patent Application Publication Sep. 17, 2015 Sheet 26 of 63 US 2015/0260527 A1 Position avia 53 Ser3 inte-face \leinery 542 Memory AC Network 34 OS APP 132 158. interface CAN S. 543 531 1549 1549 546 App APP Processing it UART USB 54 5480 S450 2C Cock Wietess interiaice 54 5498 5:00 F.G. 18A Position evice 53 After a 15495 Setia tefface Memory 1542 Memory AC Niewick Said APP 542 594 interface 1549 Processing init 5: Cock Wireless interface 15498. 50 F.G. 18B Patent Application Publication Sep. 17, 2015 Sheet 27 of 63 US 2015/0260527 A1 Afteira 54.87 Network interface Processing init 5. interface 33 Processing Unit 9 Wireless Gyroscope 953 ACCseeiO:lete 954 Bearing Device S F.G. 19 Patent Application Publication Sep. 17, 2015 Sheet 28 of 63 US 2015/0260527 A1 FG. 20 Patent Application Publication Sep. 17, 2015 Sheet 29 of 63 US 2015/0260527 A1 Pief Source 236 Power Supply 2284 Powe Sippy 2232 Weess Powe: Pier reass Poeis a Regulatof SOLFCe w O Tasite Receiver Secrea--- 228. | 22820 228. Device 24 Device 232 Power Source Power Suppy Power Source 28 258). 2361 FG. 25 Power Sippy 268: Wireless Poyer Y r Receivef va WieaSS Pow8 Regulator 2866 raisitar Device 283 Patent Application Publication Sep. 17, 2015 Sheet 30 of 63 US 2015/0260527 A1 27. 273 - F.G. 27B FG.27C Patent Application Publication Sep. 17, 2015 Sheet 31 of 63 US 2015/0260527 A1 Determine a position: 230t Determine a first bearing Deterania, utilizing the to an object second bearing a second Compute a vectof based 290 w8cc that is nosta to On the deternin88 the origin, he titject, and position the second position 282 296 Detentire a first position 29) F.G. 28A Date:re a thic w8to that is oria to the first Betermine, stizing the vec{0} and the second firs: bearing, a first vector Wector that is no inal to an oxigin, 29 the object, and the first position 233. Deter nine a position 285 Determine a position of the object 298 Deesilise 3 secois Alier a vectof easing to the Ciject corresponding to and of 294, 3SSociated with tie positio: 23.8 Deefalise a secord gosition 2335) Corpute a vector northa to e.g., perpendictatio} the position 3rd the FIG. 29 aefed Westf 23. FG. 28B Patent Application Publication Sep. 17, 2015 Sheet 32 of 63 US 2015/0260527 A1 82. 82. 3}{ 3. 8 800 8 8. F.G. 30A Patent Application Publication Sep. 17, 2015 Sheet 33 of 63 US 2015/0260527 A1 320 35 62 8. 6 SO F.G. 3OB Patent Application Publication Sep. 17, 2015 Sheet 34 of 63 US 2015/0260527 A1 Si. 3.05 32 623 35 St. FIG. 30C Patent Application Publication Sep. 17, 2015 Sheet 35 of 63 US 2015/0260527 A1 F.G. 31A Patent Application Publication Sep. 17, 2015 Sheet 36 of 63 US 2015/0260527 A1 FG. 31B Patent Application Publication Sep. 17, 2015 Sheet 37 of 63 US 2015/0260527 A1 FIG. 31C Patent Application Publication Sep. 17, 2015 Sheet 38 of 63 US 2015/0260527 A1 6220 SSSSSSsaxxx xxxxxs SSSSSSSSSSSS SSS SSSSSSSSSSSSSSSSS sys-xx-x-xxx-xx-xxxSSSSSSSSSSSSSS S&S a SSSSSSSSS SSSSSSSS SSSSSS$$$$.& SSSSSSSSSS SSSSSSSSS 3-SSSSSSSS SSSSSF s S SS SSSSSS SSSSSSS SS s & SSSSS S&S S SSSSS -SSSSS3SSSSSSSSSS-SSSSSSSSSSSSSS & SSS SSSSSSSSSSS S&& SSS SSSSSSSSSSSSSSSSSSSS S&SSSSSSSSSSSSSS & SS SSS 3&s SS SS SSS SSSSSSSSSSSSSXSSSSSSXSSSSSS S sšŠSSSS SS X SSSSSSSSSSSSSS S $$$$$$$$. S SSSSSSSSS&SSSSSSSS SSS SSSSSSSSSSSS&SSSSSS8SS 8 SSSSSSSSSSSSSŠ SSSSSSSSSSSSSSSSSSsssssssssssssssssssssssssssssssssssssss SSSSSSSSSSSSSSSSSSSSSSSSSSSS SSSSSSSSSSS&SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS S.ŠSSSSSSSS SSSSSSSSSSSSSSSSSSsssssssssssssssssssssssssssssssssss SSSSSSSSSSSSSSSSSS as-SSSssssssssssssssssssssssssssssssss SSSSSSSSSSSSSSSSSSSSSSSSSS Š S. &SSXXXXX&xxxxxxx-xxxxx SSSSSSSSSSSSSSSSS &S SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS SSSSSSSSSSSSSSSXSSSSSSSSX SSSSSSSSSSSSSSSSSSSSSSSSSSSSSŠ &S&SSSSSSSS&S&syssssssssssssssssssssssssssssssssssss SSSSSSSSSSS SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS SSSSSSSSSSSSSSSSSSS xxxYxxxxxxxSxxxxxxSSSSSSSSS3x3x3-SS33 xxxxxxyyxxxsaxs SSSSSSS sixsssssssssssssssss&SS&SSSSS&SSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSSS SSSSSSS:s SSssssssssssssssssssssssssssssss sssssssssssssssssssssssssssssssss SyS, XSSSSSSSSSSSS SSXXXxxxxxyyxxxx Ssssssssssssssssssssssssssssssss SSSSSSSSSSSSSSSSSSSSSSSSSSSSS SSSSSSSSSSSSSSSSSSSSSS S. Ssssssssssssssssssssssssss SSSSSSSSSSSSSSSSSSSSSSSSSSSSSS SSSSSSSSSSSSSSS ssssssssssssssssssssss SSSSSSSSSSSSSSSSSSSSSS S-3-3-3-3-3-3-SSS SSSSSSSSSSSSSSSSSSSSSSSSS & St. FIG. 32A Patent Application Publication Sep. 17, 2015 Sheet 39 of 63 US 2015/0260527 A1 3264 3262: 8. a-608 FIG. 32B Patent Application Publication Sep.
Load more

Recommended publications
  • Spherical Geometry
    Spherical Geometry Eric Lehman february-april 2012 2 Table of content 1 Spherical biangles and spherical triangles 3 § 1. The unit sphere . .3 § 2. Biangles . .6 § 3. Triangles . .7 2 Coordinates on a sphere 13 § 1. Cartesian versus spherical coordinates . 13 § 2. Basic astronomy . 16 § 3. Geodesics . 16 3 Spherical trigonometry 23 § 1. Pythagoras’ theorem . 23 § 2. The three laws of spherical trigonometry . 24 4 Stereographic projection 29 § 1. Definition . 29 § 2. The stereographic projection preserves the angles . 34 § 3. Images of circles . 36 5 Projective geometry 49 § 1. First description of the real projective plane . 49 § 2. The real projective plane . 52 § 3. Generalisations . 59 3 4 TABLE OF CONTENT TABLE OF CONTENT 1 Introduction The aim of this course is to show different aspects of spherical geometry for itself, in relation to applications and in relation to other geometries and other parts of mathematics. The chapters will be (mostly) independant from each other. To begin, we’l work on the sphere as Euclid did in the plane looking at triangles. Many things look alike, but there are some striking differences. The second viewpoint will be the introduction of coordinates and the application to basic astronomy. The theorem of Pytha- goras has a very nice and simple shape in spherical geometry. To contemplate spherical trigonometry will give us respect for our ancestors and navigators, but we shall skip the computations! and let the GPS do them. The stereographic projection is a marvellous tool to understand the pencils of coaxial circles and many aspects of the relation between the spherical geometry, the euclidean affine plane, the complex projective line, the real projec- tive plane, the Möbius strip and even the hyperbolic plane.
    [Show full text]
  • Primer of Celestial Navigation
    LIFEBOAT MANUAL By Lt. Comdr. A. E. Redifer, U.S.M.S. Lifeboat Training Officer, Avalon, Calif., Training Station *Indispensable to ordinary seamen preparing for the Lifeboat Examination. *A complete guide for anyone who may have to use a lifeboat. Construction, equipment, operation of lifeboats and other buoyant apparatus are here, along with the latest Government regulations which you need to know. 163 Pages More than 150 illustrations Indexed $2.00 METEOROLOGY WORKBOOK with Problems By Peter E. Kraght Senior Meteorologist, American Airlines, Inc. *Embodies author's experience in teaching hundreds of aircraft flight crews. *For self-examination and for classroom use. *For student navigator or meteorologist or weather hobbyist. *A good companion book to Mr. Kraght's Meteorology for Ship and Aircraft Operation, 0r any other standard reference work. 141 Illustrations Cloud form photographs Weather maps 148 Pages W$T x tl" Format $2.25 MERCHANT MARBMI OFFICERS' HANDBOOK By E. A. Turpin and W. A. MacEwen, Master Mariners "A valuable guide for both new candidates for . officer's license and the older, more experienced officers." Marine Engi- neering and Shipping Re$etu. An unequalled guide to ship's officers' duties, navigation, meteorology, shiphandling and cargo, ship construction and sta- bility, rules of the road, first aid and ship sanitation, and enlist- ments in the Naval Reserve all in one volume. 03 086 3rd Edition "This book will be a great help to not only beginners but to practical navigating officers." Harold Kildall, Instructor in Charge, Navigation School of the Washing- ton Technical Institute, "Lays bare the mysteries of navigation with a firm and sure touch .
    [Show full text]
  • Great Circle If the Plane Passes Through the Centre of the Sphere, and a Small Circle If the Plane Does Not Pass Through the Centre of the Sphere
    1 Assoc. Prof. Dr. Bahattin ERDOĞAN Assoc. Prof. Dr. Nursu TUNALIOĞLU Yildiz Technical University Faculty of Civil Engineering Department of Geomatic Engineering Lecture Notes 2 1. A sphere is a solid bounded by a surface every point of which is equally distant from a fixed point which is called the centre of the sphere. The straight line which joins any point of the surface with the centre is called a radius. A straight line drawn through the centre and terminated both ways by the surface is called a diameter. 3 2. The section of the surface of a sphere made by any plane is a circle. 4 5 » The section of the surface of a sphere by a plane is called a great circle if the plane passes through the centre of the sphere, and a small circle if the plane does not pass through the centre of the sphere. Thus the radius of a great circle is equal to the radius of the sphere. » On the globe, equator circle and circles of longitudes are the examples of great circle and, circles of latitudes are the example of small circle. 6 7 » Latitude: latitude lines are also known as parallels (since they are parallel to one another). The lines are actually full circles that extend around the earth and vary in length depending on where we are located. The biggest circle is at the equator and represents the earth's circumference. This line is also called a Great Circle. There can be infinitely many great circles, but only one that is a line of latitude (the equator).
    [Show full text]
  • A Disorienting Look at Euler's Theorem on the Axis of a Rotation
    A Disorienting Look at Euler’s Theorem on the Axis of a Rotation Bob Palais, Richard Palais, and Stephen Rodi 1. INTRODUCTION. A rotation in two dimensions (or other even dimensions) does not in general leave any direction fixed, and even in three dimensions it is not imme- diately obvious that the composition of rotations about distinct axes is equivalent to a rotation about a single axis. However, in 1775–1776, Leonhard Euler [8] published a remarkable result stating that in three dimensions every rotation of a sphere about its center has an axis, and providing a geometric construction for finding it. In modern terms, we formulate Euler’s result in terms of rotation matrices as fol- lows. Euler’s Theorem on the Axis of a Three-Dimensional Rotation. If R is a 3 × 3 orthogonal matrix (RTR = RRT = I) and R is proper (det R =+1), then there is a nonzero vector v satisfying Rv = v. This important fact has a myriad of applications in pure and applied mathematics, and as a result there are many known proofs. It is so well known that the general concept of a rotation is often confused with rotation about an axis. In the next section, we offer a slightly different formulation, assuming only or- thogonality, but not necessarily orientation preservation. We give an elementary and constructive proof that appears to be new that there is either a fixed vector or else a “reversed” vector, i.e., one satisfying Rv =−v. In the spirit of the recent tercentenary of Euler’s birth, following our proof it seems appropriate to survey other proofs of this famous theorem.
    [Show full text]
  • The Project Gutenberg Ebook of Spherical Trigonometry, by I
    The Project Gutenberg EBook of Spherical Trigonometry, by I. Todhunter This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this eBook or online at www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook. Title: Spherical Trigonometry For the Use of Colleges and Schools Author: I. Todhunter Release Date: August 19, 2020 [EBook #19770] Language: English Character set encoding: ISO-8859-1 *** START OF THIS PROJECT GUTENBERG EBOOK SPHERICAL TRIGONOMETRY *** Credit: K.F. Greiner, Berj Zamanian, Joshua Hutchinson andthe Online Distributed Proofreading Team at http://www.pgdp.net(This file was produced from images generously made availableby Cornell University Digital Collections SPHERICAL TRIGONOMETRY. ii SPHERICAL TRIGONOMETRY For the Use of Colleges and Schools: WITH NUMEROUS EXAMPLES. BY I. TODHUNTER, M.A., F.R.S., HONORARY FELLOW OF ST JOHN'S COLLEGE, CAMBRIDGE. FIFTH EDITION. London : MACMILLAN AND CO. 1886 [All Rights reserved.] ii Cambridge: PRINTED BY C. J. CLAY, M.A. AND SON, AT THE UNIVERSITY PRESS. PREFACE The present work is constructed on the same plan as my treatise on Plane Trigonometry, to which it is intended as a sequel; it contains all the propositions usually included under the head of Spherical Trigonometry, together with a large collection of examples for exercise.
    [Show full text]
  • 1. Introduction
    Chapter-Introduction GIS 1. INTRODUCTION. Geography is the study of Earth’s features and patterns of their variations in spatial location and time. Many questions of agricultural production are geographic in nature as the production depends on the environment and prevailing socio economic conditions, both of which vary spatially and in time. Examples are questions related to natural resources management, precision agriculture, agro- ecological classification for land use planning, regional trends and patterns in technology adaptation, agricultural productivity and income, non-Pont source pollution from agricultural lands, etc. Answering these questions requires access to large volumes of multidimensional geographical (spatial) information of weather, soils, topography, water resources, socio economic status, etc. Further, answers to even apparently simple questions require that the data from several sources be integrated in a consistent form. Geographical Information Systems or GIS enable representation and integration of such spatial information. Geographic information systems (GIS) (also known as Geospatial information systems) are Computer Software and hardware systems that enable users to capture, store, analyze and manage spatially referenced data. GISs have transformed the way spatial (geographic) data, relationships and patterns in the world are able to be interactively queried, processed, analyzed, mapped, modelled, visualized, and displayed for an increasingly large range of users, for a multitude of purposes. In a general sense, the term describes any information system that integrates, stores, edits, analyzes, shares, and displays geographic information. GIS applications are tools that allow users to create interactive queries (user-created searches), analyze spatial information, edit data in maps, and present the results of all these operations.
    [Show full text]
  • Xivth CONGRESS of the INTERNATIONAL SOCIETY for P1IOTOGRN1HETRY
    XIVth CONGRESS OF THE INTERNATIONAL SOCIETY FOR P1IOTOGRN1HETRY Hamburg, 1980 COWHSSiotT VI Report of Working Group-3 TRI-LINGUAL GLOSSARY OF PHOTOGRAHNETRY TER.HS Dr. Paul R. Half University of Wisconsin Nadison, Wisconsin, U.S.A. The activities of Vlorking Group-3 of Commission VI during the four year period from 1976 to 1980 are summarized. A draft version of definitions of common photogrammetry terms which are the result of this work is attached. This draft is intended to serve as the basis for developing the final version of the Photogrammetry part of the ISP Tri-Lingual Glossary of Terms. Recommendations are made for the inclusion of Remote Sensing terms in the final Glossary. 199 1 I. Introduction At the XIII Congress of the International Society for Photo­ grammetry at Helsinki, Finland in 1976, the following resolution was recommended by ComNission VI, and was adopted by the General Assembly: "Commission VI has noted that the continuously increasing fields of application of Photogrammetry and Remote Sensing would involve them in Nore diverse activities among fellow photogrammetrists and with colleagues in other associated branches of science and engineering. This demands continuous exchange of ideas with regard to "Notations and Terminology. It is, therefore, recommended that such activities be pursued with more vigor by continuing the efforts in one working group and that an appropriate multi-lingual glossary be developed for submission to the XIV Congress in 1980." Working Group-3 was organized for the purpose of carrying out the objectives of this resolution. A committee for Harking Group-3 was appointed and consisted of Dr.
    [Show full text]
  • Chapter 1- Mathematics
    CHAPTER 1 MATHEMATICS ARITHMETIC 4 100. Definition numbers in powers of 10. Thus, 18.6×10 (18.6 x 10,000) in- 4 dicates accuracy to the nearest thousand, 18.60×10 to the Arithmetic is that branch of mathematics dealing with 4 computation by numbers. The principal processes involved nearest hundred, 18.600×10 to the nearest ten, and 4 are addition, subtraction, multiplication, and division. A 18.6000×10 to the nearest unit. The position of the decimal number consisting of a single symbol (1, 2, 3, etc.) is a is not important if the correct power of 10 is given. For ex- 4 6 3 digit. Any number that can be stated or indicated, however ample, 18.6×10 is the same as 1.86×10 , 186×10 , etc. The large or small, is called a finite number; one too large to be small number above and to the right of 10 (the exponent) stated or indicated is called an infinite number; and one indicates the number of places the decimal point is to be too small to be stated or indicated is called an infinitesimal moved to the right. If the exponent is negative, it indicates number. a reciprocal, and the decimal point is moved to the left. The sign of a number is the indication of whether it is Thus, 1.86× 10–6 is the same as 0.00000186. This system is positive (+) or negative (-). This may sometimes be indi- called scientific notation. cated in another way. Thus, latitude is usually indicated as north (N) or south (S), but if north is considered positive, 102.
    [Show full text]
  • Twisted Curves
    CHAPTER XX. RECTIFICATION OF TWISTED CURVES. 706. Let PQ be any elementary arc δs of the curve. Let the coordinates of P and Q be respectively and with regard to any three fixed rectangular axes Ox, 0y, Oz. Then Nbw, if Q be made to travel along the curve so as to approach indefinitely near to P, the chord PQ and the arc PQ ultimately differ by an infinitesimal of higher order than the arc PQ itself, i.e. the chord PQ and the arc PQ ultimately vanish in a ratio of equality.* Hence we have to the second order of small quantities, (1) Now suppose the curve to be specified in one of the two usual ways, (a) as the line of intersection of two specified surfaces or (b) the coordinates of any point x, y, z upon it expressed in terms of some fourth variable t, and defined by the equations The First Case. In Case (α) choice must be made of one of the three vari­ ables x, y, z to be considered as the independent variable, say x, and the equations f=0, F=0 are then to be solved to find *For a discussion of this point see De Morgan, Differential and Integral, Calculus, p. 445. See also Diff. Calc., Art. 34, for a plane curve. 732 www.rcin.org.pl TWISTED CURVES. 733 the other two, y and z, in terms of x. Then differentiating, we express and in terms of x; say We then have And when the integration has been effected, the length of the arc between the points specified by any particular limits which may be assigned to x, will have been obtained.
    [Show full text]
  • STARLAB Portable Planetarium System
    STARLAB Portable Planetarium System — Part C — Grades 7-12 Activities and Lessons for Use in the STARLAB Portable Planetarium Compiled, edited & revised by Joyce Kloncz, Gary D. Kratzer and Andrea Colby ©2008 by Science First/STARLAB, 95 Botsford Place, Buffalo, NY 14216. www.starlab.com. All rights reserved. Table of Contents Part C — Grades 7-12 Activities and Lessons Using the Curriculum Guide for Astronomy and IX. Topic of Study: Winter Constellations ...............C-26 Interdisciplinary Topics in Grades 7-12 X. Topic of Study: Spring Constellations ................C-27 Introduction .........................................................C-5 XI. Topic of Study: Summer Constellations .............C-28 Curriculum Guide for Astronomy and XII. Topic of Study: Mapping the Stars I — Interdisciplinary Topics in Grades 7-12 Circumpolar, Fall and Winter ..............................C-29 Sciences: Earth, Life, Physical and Space XIII. Topic of Study: Mapping the Stars II — Topic of Study 1: Earth as an Astronomical Object ..C-6 Circumpolar, Spring and Summer ........................C-30 Topic of Study 2: Latitude and Longitude .................C-7 XIV. Topic of Study: The Age of Aquarius ..............C-30 Topic of Study 3: The Earth's Atmosphere ...............C-7 XV. Topic of Study: Mathematics — As it Relates to Astronomy .....................................................C-31 Topic of Study 4: The Sun and Its Energy ................C-8 XVI. Topic of Study: Calculating Time from the Topic of Study 5: The Stars ....................................C-9
    [Show full text]
  • Mathematical Methods in Ptolemy's Analemma
    Mathematical Methods in Ptolemy’s Analemma Nathan Sidoli 1. Introduction This paper is an attempt to understand the mathematical methods found in Ptolemy’s Analemma in the context of Greek mathematical practices. I first present an overview of the concepts we will need to read the text, followed by a close reading of select passages, which provide a clear overview of the structure of the argument and give examples of the mathematical methods involved. In general terms, the Analemma provides a method for specifying the location of the sun in three pairs of locally orientated coordinate arcs as a function of three ostensibly empirical variables, namely the declination of the sun as a function of its longitude, δ(λ), the terrestrial latitude, φ, and the hour, η. The key to the approach is to represent the solid configuration in a plane diagram that Ptolemy calls the analemma. The mathematical argument begins with the presentation of a general argument that the analemma figure, or model, can be used to map arcs and lines of the solid configuration, through the example of a proof that this mapping is sound for one of the angles in question. It then proceeds to show that the analemma figure can be used to make computations of arc lengths of the solid sphere through two different methods: chord-table trigonometry, or what we can call analog, or nomographic, computation.1 The final section of the received text details a series of physical manipulations through which we can compute the values of three pairs of coordinate arcs given the three variables δ(λ), φ, and η.
    [Show full text]
  • A Disorienting Look at Euler's Theorem on The
    Integre Technical Publishing Co., Inc. American Mathematical Monthly 116:10 August 25, 2009 1:46 p.m. palais.tex page 892 A Disorienting Look at Euler’s Theorem on the Axis of a Rotation Bob Palais, Richard Palais, and Stephen Rodi 1. INTRODUCTION. A rotation in two dimensions (or other even dimensions) does not in general leave any direction fixed, and even in three dimensions it is not imme- diately obvious that the composition of rotations about distinct axes is equivalent to a rotation about a single axis. However, in 1775–1776, Leonhard Euler [8] published a remarkable result stating that in three dimensions every rotation of a sphere about its center has an axis, and providing a geometric construction for finding it. In modern terms, we formulate Euler’s result in terms of rotation matrices as fol- lows. Euler’s Theorem on the Axis of a Three-Dimensional Rotation. If R is a 3 × 3 orthogonal matrix (RTR = RRT = I) and R is proper (det R =+1), then there is a nonzero vector v satisfying Rv = v. This important fact has a myriad of applications in pure and applied mathematics, and as a result there are many known proofs. It is so well known that the general concept of a rotation is often confused with rotation about an axis. In the next section, we offer a slightly different formulation, assuming only or- thogonality, but not necessarily orientation preservation. We give an elementary and constructive proof that appears to be new that there is either a fixed vector or else a “reversed” vector, i.e., one satisfying Rv =−v.
    [Show full text]