Appendixb.Tex
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Quaternions and Cli Ord Geometric Algebras
Quaternions and Cliord Geometric Algebras Robert Benjamin Easter First Draft Edition (v1) (c) copyright 2015, Robert Benjamin Easter, all rights reserved. Preface As a rst rough draft that has been put together very quickly, this book is likely to contain errata and disorganization. The references list and inline citations are very incompete, so the reader should search around for more references. I do not claim to be the inventor of any of the mathematics found here. However, some parts of this book may be considered new in some sense and were in small parts my own original research. Much of the contents was originally written by me as contributions to a web encyclopedia project just for fun, but for various reasons was inappropriate in an encyclopedic volume. I did not originally intend to write this book. This is not a dissertation, nor did its development receive any funding or proper peer review. I oer this free book to the public, such as it is, in the hope it could be helpful to an interested reader. June 19, 2015 - Robert B. Easter. (v1) [email protected] 3 Table of contents Preface . 3 List of gures . 9 1 Quaternion Algebra . 11 1.1 The Quaternion Formula . 11 1.2 The Scalar and Vector Parts . 15 1.3 The Quaternion Product . 16 1.4 The Dot Product . 16 1.5 The Cross Product . 17 1.6 Conjugates . 18 1.7 Tensor or Magnitude . 20 1.8 Versors . 20 1.9 Biradials . 22 1.10 Quaternion Identities . 23 1.11 The Biradial b/a . -

Codimension One Isometric Immersions Betweenlorentz Spaces by L
TRANSACTIONS OF THE AMERICAN MATHEMATICAL SOCIETY Volume 252, August 1979 CODIMENSION ONE ISOMETRIC IMMERSIONS BETWEENLORENTZ SPACES BY L. K. GRAVES In memory of my father, Lucius Kingman Graves Abstract. The theorem of Hartman and Nirenberg classifies codimension one isometric immersions between Euclidean spaces as cylinders over plane curves. Corresponding results are given here for Lorentz spaces, which are Euclidean spaces with one negative-definite direction (also known as Minkowski spaces). The pivotal result involves the completeness of the relative nullity foliation of such an immersion. When this foliation carries a nondegenerate metric, results analogous to the Hartman-Nirenberg theorem obtain. Otherwise, a new description, based on particular surfaces in the three-dimensional Lorentz space, is required. The theorem of Hartman and Nirenberg [HN] says that, up to a proper motion of E"+', all isometric immersions of E" into E"+ ' have the form id X c: E"-1 xEUr'x E2 (0.1) where c: E1 ->E2 is a unit speed plane curve and the factors in the product are orthogonal. A proof of the Hartman-Nirenberg result also appears in [N,]. The major step in proving the theorem is showing that the relative nullity foliation, which is spanned by those tangent directions in which a local unit normal field is parallel, has complete leaves. These leaves yield the E"_1 factors in (0.1). The one-dimensional complement of the relative nullity foliation gives rise to the curve c. This paper studies isometric immersions of L" into Ln+1, where L" denotes the «-dimensional Lorentz (or Minkowski) space. Its chief goal is the classifi- cation, up to a proper motion of L"+1, of all such immersions. -

Embeddings of Integral Quadratic Forms Rick Miranda Colorado State
Embeddings of Integral Quadratic Forms Rick Miranda Colorado State University David R. Morrison University of California, Santa Barbara Copyright c 2009, Rick Miranda and David R. Morrison Preface The authors ran a seminar on Integral Quadratic Forms at the Institute for Advanced Study in the Spring of 1982, and worked on a book-length manuscript reporting on the topic throughout the 1980’s and early 1990’s. Some new results which are proved in the manuscript were announced in two brief papers in the Proceedings of the Japan Academy of Sciences in 1985 and 1986. We are making this preliminary version of the manuscript available at this time in the hope that it will be useful. Still to do before the manuscript is in final form: final editing of some portions, completion of the bibliography, and the addition of a chapter on the application to K3 surfaces. Rick Miranda David R. Morrison Fort Collins and Santa Barbara November, 2009 iii Contents Preface iii Chapter I. Quadratic Forms and Orthogonal Groups 1 1. Symmetric Bilinear Forms 1 2. Quadratic Forms 2 3. Quadratic Modules 4 4. Torsion Forms over Integral Domains 7 5. Orthogonality and Splitting 9 6. Homomorphisms 11 7. Examples 13 8. Change of Rings 22 9. Isometries 25 10. The Spinor Norm 29 11. Sign Structures and Orientations 31 Chapter II. Quadratic Forms over Integral Domains 35 1. Torsion Modules over a Principal Ideal Domain 35 2. The Functors ρk 37 3. The Discriminant of a Torsion Bilinear Form 40 4. The Discriminant of a Torsion Quadratic Form 45 5. -

Introduction to Clifford's Geometric Algebra
SICE Journal of Control, Measurement, and System Integration, Vol. 4, No. 1, pp. 001–011, January 2011 Introduction to Clifford’s Geometric Algebra ∗ Eckhard HITZER Abstract : Geometric algebra was initiated by W.K. Clifford over 130 years ago. It unifies all branchesof physics, and has found rich applications in robotics, signal processing, ray tracing, virtual reality, computer vision, vector field processing, tracking, geographic information systems and neural computing. This tutorial explains the basics of geometric algebra, with concrete examples of the plane, of 3D space, of spacetime, and the popular conformal model. Geometric algebras are ideal to represent geometric transformations in the general framework of Clifford groups (also called versor or Lipschitz groups). Geometric (algebra based) calculus allows, e.g., to optimize learning algorithms of Clifford neurons, etc. Key Words: Hypercomplex algebra, hypercomplex analysis, geometry, science, engineering. 1. Introduction unique associative and multilinear algebra with this property. W.K. Clifford (1845-1879), a young English Goldsmid pro- Thus if we wish to generalize methods from algebra, analysis, ff fessor of applied mathematics at the University College of Lon- calculus, di erential geometry (etc.) of real numbers, complex don, published in 1878 in the American Journal of Mathemat- numbers, and quaternion algebra to vector spaces and multivec- ics Pure and Applied a nine page long paper on Applications of tor spaces (which include additional elements representing 2D Grassmann’s Extensive Algebra. In this paper, the young ge- up to nD subspaces, i.e. plane elements up to hypervolume el- ff nius Clifford, standing on the shoulders of two giants of alge- ements), the study of Cli ord algebras becomes unavoidable. -

Zeros of Conformal Fields in Any Metric Signature
Zeros of conformal fields in any metric signature Andrzej Derdzinski Department of Mathematics, The Ohio State University, Columbus, OH 43210, USA E-mail: [email protected] Abstract. The connected components of the zero set of any conformal vector field, in a pseudo-Riemannian manifold of arbitrary signature, are shown to be totally umbilical conifold varieties, that is, smooth submanifolds except possibly for some quadric singularities. The singularities occur only when the metric is indefinite, including the Lorentzian case. This generalizes an analogous result for Riemannian manifolds, due to Belgun, Moroianu and Ornea (2010). AMS classification scheme numbers: 53B30 1. Introduction A vector field v on a pseudo-Riemannian manifold (M; g) of dimension n ≥ 2 is called conformal if, for some function φ : M ! IR, $vg = φg; that is; in coordinates; vj;k + vk;j = φgjk : (1) One then obviously has div v = nφ/2. The class of conformal vector fields on (M; g) includes Killing fields v, characterized by (1) with φ = 0. Kobayashi [15] showed that, for any Killing vector field v on a Riemannian manifold (M; g), the connected components of the zero set of v are mutually isolated totally geodesic submanifolds of even codimensions. Assuming compactness of M, Blair [5] established an analogue of Kobayashi's theorem for conformal vector fields, in which the word `geodesic' is replaced by `umbilical' and the codimension clause is relaxed for one-point connected components. Very recently, Belgun, Moroianu and Ornea [4] proved that Blair's conclusion is valid in the noncompact case as well. The last result is also a direct consequence of a theorem of Frances [12] stating that a conformal field on a Riemannian manifold is linearizable at any zero z unless some neighborhood of z is conformally flat. -

Notes on Geometry and Spacetime Version 2.7, November 2009
Notes on Geometry and Spacetime Version 2.7, November 2009 David B. Malament Department of Logic and Philosophy of Science University of California, Irvine [email protected] Contents 1 Preface 2 2 Preliminary Mathematics 2 2.1 Vector Spaces . 3 2.2 Affine Spaces . 6 2.3 Metric Affine Spaces . 15 2.4 Euclidean Geometry . 21 3 Minkowskian Geometry and Its Physical Significance 28 3.1 Minkowskian Geometry { Formal Development . 28 3.2 Minkowskian Geometry { Physical Interpretation . 39 3.3 Uniqueness Result for Minkowskian Angular Measure . 51 3.4 Uniqueness Results for the Relative Simultaneity Relation . 56 4 From Minkowskian Geometry to Hyperbolic Plane Geometry 64 4.1 Tarski's Axioms for first-order Euclidean and Hyperbolic Plane Geometry . 64 4.2 The Hyperboloid Model of Hyperbolic Plane Geometry . 69 These notes have not yet been fully de-bugged. Please read them with caution. (Corrections will be much appreciated.) 1 1 Preface The notes that follow bring together a somewhat unusual collection of topics. In section 3, I discuss the foundations of \special relativity". I emphasize the invariant, \geometrical approach" to the theory, and spend a fair bit of time on one special topic: the status of the relative simultaneity relation within the theory. At issue is whether the standard relation, the one picked out by Einstein's \definition" of simultaneity, is conventional in character, or is rather in some significant sense forced on us. Section 2 is preparatory. When the time comes, I take \Minkowski space- time" to be a four-dimensional affine space endowed with a Lorentzian inner product. -

Topological Vector Spaces
Topological Vector Spaces Maria Infusino University of Konstanz Winter Semester 2015/2016 Contents 1 Preliminaries3 1.1 Topological spaces ......................... 3 1.1.1 The notion of topological space.............. 3 1.1.2 Comparison of topologies ................. 6 1.1.3 Reminder of some simple topological concepts...... 8 1.1.4 Mappings between topological spaces........... 11 1.1.5 Hausdorff spaces...................... 13 1.2 Linear mappings between vector spaces ............. 14 2 Topological Vector Spaces 17 2.1 Definition and main properties of a topological vector space . 17 2.2 Hausdorff topological vector spaces................ 24 2.3 Quotient topological vector spaces ................ 25 2.4 Continuous linear mappings between t.v.s............. 29 2.5 Completeness for t.v.s........................ 31 1 3 Finite dimensional topological vector spaces 43 3.1 Finite dimensional Hausdorff t.v.s................. 43 3.2 Connection between local compactness and finite dimensionality 46 4 Locally convex topological vector spaces 49 4.1 Definition by neighbourhoods................... 49 4.2 Connection to seminorms ..................... 54 4.3 Hausdorff locally convex t.v.s................... 64 4.4 The finest locally convex topology ................ 67 4.5 Direct limit topology on a countable dimensional t.v.s. 69 4.6 Continuity of linear mappings on locally convex spaces . 71 5 The Hahn-Banach Theorem and its applications 73 5.1 The Hahn-Banach Theorem.................... 73 5.2 Applications of Hahn-Banach theorem.............. 77 5.2.1 Separation of convex subsets of a real t.v.s. 78 5.2.2 Multivariate real moment problem............ 80 Chapter 1 Preliminaries 1.1 Topological spaces 1.1.1 The notion of topological space The topology on a set X is usually defined by specifying its open subsets of X. -

Lecture Notes on General Relativity Columbia University
Lecture Notes on General Relativity Columbia University January 16, 2013 Contents 1 Special Relativity 4 1.1 Newtonian Physics . .4 1.2 The Birth of Special Relativity . .6 3+1 1.3 The Minkowski Spacetime R ..........................7 1.3.1 Causality Theory . .7 1.3.2 Inertial Observers, Frames of Reference and Isometies . 11 1.3.3 General and Special Covariance . 14 1.3.4 Relativistic Mechanics . 15 1.4 Conformal Structure . 16 1.4.1 The Double Null Foliation . 16 1.4.2 The Penrose Diagram . 18 1.5 Electromagnetism and Maxwell Equations . 23 2 Lorentzian Geometry 25 2.1 Causality I . 25 2.2 Null Geometry . 32 2.3 Global Hyperbolicity . 38 2.4 Causality II . 40 3 Introduction to General Relativity 42 3.1 Equivalence Principle . 42 3.2 The Einstein Equations . 43 3.3 The Cauchy Problem . 43 3.4 Gravitational Redshift and Time Dilation . 46 3.5 Applications . 47 4 Null Structure Equations 49 4.1 The Double Null Foliation . 49 4.2 Connection Coefficients . 54 4.3 Curvature Components . 56 4.4 The Algebra Calculus of S-Tensor Fields . 59 4.5 Null Structure Equations . 61 4.6 The Characteristic Initial Value Problem . 69 1 5 Applications to Null Hypersurfaces 73 5.1 Jacobi Fields and Tidal Forces . 73 5.2 Focal Points . 76 5.3 Causality III . 77 5.4 Trapped Surfaces . 79 5.5 Penrose Incompleteness Theorem . 81 5.6 Killing Horizons . 84 6 Christodoulou's Memory Effect 90 6.1 The Null Infinity I+ ................................ 90 6.2 Tracing gravitational waves . 93 6.3 Peeling and Asymptotic Quantities . -
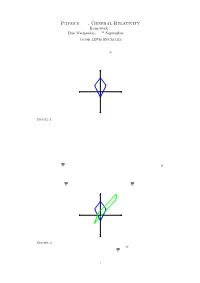
Physics 523, General Relativity
Physics 523, General Relativity Homework 1 Due Wednesday, 27th September 2006 Jacob Lewis Bourjaily Problem 1 a) We are to use the spacetime diagram of an observer O to describe an `experiment' speci¯ed by the problem 1.5 in Schutz' text. We have shown the spacetime diagram in Figure 1 below. t x Figure 1. A spacetime diagram representing the experiment which was required to be described in Problem 1.a. b) The experimenter observes that the two particles arrive back at the same point in spacetime after leaving from equidistant sources. The experimenter argues that this implies that they were released `simultaneously;' comment. In his frame, his reasoning is just, and implies that his t-coordinates of the two events have the same value. However, there is no absolute simultaneity in spacetime, so a di®erent observer would be free to say that in her frame, the two events were not simultaneous. c) A second observer O moves with speed v = 3c=4 in the negative x-direction relative to O. We are asked to draw the corresponding spacetime diagram of the experiment in this frame and comment on simultaneity. Calculating the transformation by hand (so the image is accurate), the experiment ob- served in frame O is shown in Figure 2. Notice that observer O does not see the two emission events as occurring simultaneously. t x Figure 2. A spacetime diagram representing the experiment in two di®erent frames. The worldlines in blue represent those recorded by observer O and those in green rep- resent the event as recorded by an observer in frame O. -

Geometric Algebra: an Introduction with Applications in Euclidean and Conformal Geometry
San Jose State University SJSU ScholarWorks Master's Theses Master's Theses and Graduate Research Fall 2013 Geometric Algebra: An Introduction with Applications in Euclidean and Conformal Geometry Richard Alan Miller San Jose State University Follow this and additional works at: https://scholarworks.sjsu.edu/etd_theses Recommended Citation Miller, Richard Alan, "Geometric Algebra: An Introduction with Applications in Euclidean and Conformal Geometry" (2013). Master's Theses. 4396. DOI: https://doi.org/10.31979/etd.chd4-za3f https://scholarworks.sjsu.edu/etd_theses/4396 This Thesis is brought to you for free and open access by the Master's Theses and Graduate Research at SJSU ScholarWorks. It has been accepted for inclusion in Master's Theses by an authorized administrator of SJSU ScholarWorks. For more information, please contact [email protected]. GEOMETRIC ALGEBRA: AN INTRODUCTION WITH APPLICATIONS IN EUCLIDEAN AND CONFORMAL GEOMETRY A Thesis Presented to The Faculty of the Department of Mathematics and Statistics San Jos´eState University In Partial Fulfillment of the Requirements for the Degree Master of Science by Richard A. Miller December 2013 ⃝c 2013 Richard A. Miller ALL RIGHTS RESERVED The Designated Thesis Committee Approves the Thesis Titled GEOMETRIC ALGEBRA: AN INTRODUCTION WITH APPLICATIONS IN EUCLIDEAN AND CONFORMAL GEOMETRY by Richard A. Miller APPROVED FOR THE DEPARTMENT OF MATHEMATICS AND STATISTICS SAN JOSE´ STATE UNIVERSITY December 2013 Dr. Richard Pfiefer Department of Mathematics and Statistics Dr. Richard Kubelka Department of Mathematics and Statistics Dr. Wasin So Department of Mathematics and Statistics ABSTRACT GEOMETRIC ALGEBRA: AN INTRODUCTION WITH APPLICATIONS IN EUCLIDEAN AND CONFORMAL GEOMETRY by Richard A. Miller This thesis presents an introduction to geometric algebra for the uninitiated. -

The Four Dimensional Dirac Equation in Five Dimensions
The Four Dimensional Dirac Equation in Five Dimensions Romulus Breban Institut Pasteur, Paris, France Abstract The Dirac equation may be thought as originating from a theory of five-dimensional (5D) space- time. We define a special 5D Clifford algebra and introduce a spin-1/2 constraint equation to describe null propagation in a 5D space-time manifold. We explain how the 5D null formalism breaks down to four dimensions to recover two single-particle theories. Namely, we obtain Dirac’s relativistic quantum mechanics and a formulation of statistical mechanics. Exploring the non-relativistic limit in five and four dimensions, we identify a new spin-electric interaction with possible applications to magnetic resonance spectroscopy (within quantum mechanics) and superconductivity (within statistical mechanics). 1 Introduction The Dirac equation [1, 2] established itself as a fundamental tool in four dimensional (4D) physics. With increasing popularity of 5D physics, many authors generalized it from four to five dimensions [3–12]. A different approach was that of Barut [13] who recognized that the Dirac matrices αj (j, k, ... =1, 2, 3) and β close under commutation to provide a representation of so(1,4), thus establishing an intrinsic 5D symmetry of the Dirac equation. Later, Bracken and Cohen [14] introduced an algebraic formalism, for the Dirac equation, based on so(1,4). In this paper, we present a curved geometry for 5D space-times compatible to the Dirac equation, where the electromagnetic field enters according to the minimal coupling recipe. Furthermore, we reconsider the non-relativistic limit of the Dirac equation using 5D-based approximations. -

Linear Extenders and the Axiom of Choice
LINEAR EXTENDERS AND THE AXIOM OF CHOICE MARIANNE MORILLON Abstract. In set theory without the axiom of Choice ZF, we prove that for every commu- tative field K, the following statement DK: “On every non null K-vector space, there exists a non null linear form” implies the existence of a “K-linear extender” on every vector subspace of a K-vector space. This solves a question raised in [9]. In the second part of the paper, we generalize our results in the case of spherically complete ultrametric valued fields, and show that Ingleton’s statement is equivalent to the existence of “isometric linear extenders”. 1. Introduction We work in ZF, set theory without the Axiom of Choice (AC). Given a commutative field K and two K-vector spaces E, F , we denote by LK(E, F ) (or L(E, F )) the set of K-linear mappings T : E → F . Thus, L(E, F ) is a vector subspace of the product vector space F E. A linear form on the K-vector space E is a K-linear mapping f : E → K; we denote by E∗ the algebraic dual of E, i.e. the vector space L(E, K). Given two K-vector spaces E1 and t ∗ ∗ E2, and a linear mapping T : E1 → E2, we denote by T : E2 → E1 the mapping associating ∗ t to every g ∈ E2 the linear mapping g ◦ T : E1 → K: the mapping T is K-linear and is called the transposed mapping of T . Given a vector subspace F of the K-vector space E, a linear extender for F in E is a linear mapping T : F ∗ → E∗ associating to each linear form f ∈ F ∗ a linear form f˜ : E → K extending f.