DOCSLIB.ORG

Induced Drag and High-Speed Aerodynamics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Induced Drag and High-Speed Aerodynamics Induced Drag and High-Speed Aerodynamics Robert Stengel, Aircraft Flight Dynamics, MAE 331, 2018 • Drag-due-to-lift and effects of wing planform • Effect of angle of attack on lift and drag coefficients • Mach number (i.e., air compressibility) effects on aerodynamics • Newtonian approximation for lift and drag Reading: Flight Dynamics Aerodynamic Coefficients, 85-96 Airplane Stability and Control Chapter 1 Copyright 2018 by Robert Stengel. All rights reserved. For educational use only. http://www.princeton.edu/~stengel/MAE331.html http://www.princeton.edu/~stengel/FlightDynamics.html 1 Induced Drag 2 1 Aerodynamic Drag 1 1 Drag = C ρV 2S ≈ C + εC 2 ρV 2S D 2 ( D0 L ) 2 2 1 ≈ ⎡C + ε C + C α ⎤ ρV 2S ⎣⎢ D0 ( Lo Lα ) ⎦⎥ 2 3 2 Induced Drag of a Wing, εCL § Lift produces downwash (angle proportional to lift) § Downwash rotates local velocity vector clockwise in figure § Lift is perpendicular to velocity vector § Axial component of rotated lift induces drag § But what is the proportionality factor, ε? 4 2 Induced Angle of Attack C C sin , where Di = L α i α i = CL πeAR, Induced angle of attack C = C sin C πeAR C 2 πeAR Di L ( L ) ! L 5 Three Expressions for Induced Drag of a Wing C 2 C 2 1+δ C L L ( ) C 2 Di = ! ! ε L πeAR π AR e = Oswald efficiency factor = 1 for elliptical distribution δ = departure from ideal elliptical lift distribution 1 (1+δ ) ε = = πeAR π AR 6 3 Spanwise Lift Distribution of Elliptical and Trapezoidal Wings Straight Wings (@ 1/4 chord), McCormick Spitfire TR = taper ratio, λ P-51D Mustang For some taper ratio between 0.35 and 1, trapezoidal lift distribution is nearly elliptical 7 Induced Drag Factor, δ 2 CL (1+ δ ) C = Di π AR • Graph for δ (McCormick, p. 172) Lower AR 8 4 Oswald Efficiency Factor, e C 2 C = L Di πeAR Empirical approximations for e Pamadi AR λ κ = cosΛLE R = 0.0004κ 3 − 0.008κ 2 + 0.05κ + 0.86 1.1C e ≈ Lα RCL + (1− R)π AR Raymer α e ≈ 1.78(1− 0.045AR0.68 ) − 0.64 [Straight wing] 0.68 0.15 e ≈ 4.61(1− 0.045AR )(cosΛLE ) − 3.1 [Swept wing] 9 Maximum Lift-to-Drag Ratio Maximize L/D by proper choice of CL L C C ∂(L / D) = L = L = 0 D C C C 2 C D Do + ε L ∂ L C + εC 2 − C 2εC C − εC 2 ∂(L / D) ( Do L ) L ( L ) ( Do L ) = 0 = 2 = 2 2 2 ∂CL C + εC C + εC ( Do L ) ( Do L ) C 1 Do (L / D) = (CL ) = max (L/D)max 2 εC ε Do 10 5 Lift and Drag Coefficients Over Large Angles of Attack (0< α < 90) All coefficients converge to Newtonian-like values at very high angle of attack Low-AR wing has less drag than high-AR wing at given α 11 Lift vs. Drag for Large Variation in Angle of Attack (0< α < 90) Subsonic Lift-Drag Polar Low-AR wing has less drag than high-AR wing, but less lift as well High-AR wing has the best overall subsonic L/D 12 6 Lift-to-Drag Ratio vs. Angle of Attack • Performance metric for aircraft • High-AR wing: Best overall subsonic L/D • Low-AR wing: Best L/D at high angle of attack L C q S C = L = L D CDq S CD 13 € Newtonian Flow and Aerodynamic Forces 14 7 Newtonian Flow • No circulation • Cookie-cutter flow • Equal pressure across bottom of a flat plate • Flow brought to a halt at the surface 15 Newtonian Flow Normal Force ⎛ Mass flow rate⎞ Normal Force = ⎝⎜ Unit area ⎠⎟ × (Change in velocity) Projected Area × ( ) × (Angle between plate and velocity) N = (ρV )(V − 0)(Ssinα )(sinα ) = ρV 2 Ssin2 α ( )( ) 2 2 ⎛ 1 2 ⎞ CN = 2sin α = 2sin α ρV S ( )⎝⎜ 2 ⎠⎟ α = Incident flow angle ⎛ 1 2 ⎞ ≡ C ρV S 16 N ⎝⎜ 2 ⎠⎟ 8 Newtonian Forces on a Flat Plate Normal Force Coefficient 2 CN = 2sin α Lift and Drag Lift = N cosα 2 CL = (2sin α )cosα Drag = N sinα C = 2sin3 α D 17 Aerodynamic Force Estimation for a Hypersonic Aircraft Integrate differential normal force over the aircraft surface, accounting for varying surface incidence (i.e., angle) to the flow ! f $ ! X $ # x & # B & f fB = ∫ # y &dx dydz = # YB & Surface# & # & f Z "# z %& " B % 18 9 Application of Newtonian Flow Space Shuttle in • But where does the airflow go? Supersonic Flow • Hypersonic flow (M ~> 5) – Shock wave close to surface (thin shock layer), merging with the boundary layer – Flow is ~ parallel to the surface High-Angle-of- – Separated upper surface flow Attack Research Vehicle (F-18) • All Mach numbers at high angle of attack – Separated flow on upper (leeward) surfaces Flat Plate, Re = 50,000 19 Historical Factoid Conversions from Propellers to Jets Douglas XB-43 Douglas XB-42 Mixmaster Northrop XB-49 Northrop YB-35 Convair B-36 Convair YB-60 20 10 Historical Factoid Jets at an Awkward Age • Performance of first jet aircraft outstripped stability and control North American B-45 technology – Lacked satisfactory actuators, sensors, and control electronics Lockheed P-80 – Transistor: 1947, integrated circuit: 1958 • Dramatic dynamic variations over larger flight envelope – Control mechanisms designed to Douglas F3D lighten pilot loads were subject to instability • Reluctance of designers to embrace change, fearing decreased reliability, increased cost, and higher weight 21 Convair XP-81 Mach Number Effects True Airspeed Mach Number = Speed of Sound Supersonic Bullet, Ernst Mach 1888 Schlieren 1838-1916 photograph 22 11 Drag Due to Pressure Differential S 0.029 S C = C base ≈ base M < 1 Hoerner Dbase pressurebase S ( ) [ ] Swet S C friction Blunt base Sbase pressure drag 2 ⎛ Sbase ⎞ < 2 ⎜ ⎟ (M > 2, γ = specific heat ratio) γ M ⎝ S ⎠ C Dincompressible CD ≈ (M <1) “The Sonic Barrier” wave 1− M 2 Prandtl C Dcompressible factor ≈ (M >1) M 2 −1 CD ≈ M ≈ 2 (M >1) M 2 −1 23 Shock Waves in Supersonic Flow Air Compressibility Effect • Drag rises due to pressure increase across a shock wave • Subsonic flow – Local airspeed less than sonic (i.e., speed of sound) everywhere • Transonic flow – Airspeed less than sonic at some points, greater than sonic elsewhere • Supersonic flow • Critical Mach number – Local airspeed greater than – Mach number at which local sonic virtually everywhere flow first becomes sonic – Onset of drag-divergence – Mcrit ~ 0.7 to 0.85 24 12 Effect of Chord Thickness on Wing Lockheed P-38 Pressure Drag Lockheed F-104 • Thinner chord sections lead to higher Mcrit, or drag-divergence Mach number 25 Air Compressibility Effect on Wing Drag Sonic Booms http://www.youtube.com/watch?v=gWGLAAYdbbc Transonic Supersonic Subsonic Incompressible 26 13 Pressure Drag on Wing Depends on Sweep Angle M crit M = unswept critswept cos Λ Talay, NASA SP-367 27 Historical Factoid From Straight to Swept Wings • Straight-wing models were redesigned with swept wings to reduce compressibility effects on drag and increase speed • Dramatic change in stability, control, and flying qualities North American FJ-1 and Republic F-84B Thunderbird and Grumman F9F-2 Panther and FJ-4 Fury F-84F Thunderstreak F9F-6 Cougar 28 14 Airbus A320 Supercritical Wing NASA Supercritical Wing F-8 • Richard Whitcombs supercritical airfoil – Wing upper surface flattened to increase Mcrit – Wing thickness can be restored • Important for structural efficiency, fuel storage, etc. (–) (+) Pressure Distribution on Supercritical Airfoil ~ Section Lift 29 Subsonic Air Compressibility and Sweep Effects on 3-D Wing Lift Slope • Subsonic 3-D wing, with sweep effect π AR CL = α + 2 . $ AR ' -1+ 1+& ) 1− M 2 cosΛ 0 - &2cosΛ ) ( 1 4 )0 ,- % 1 4 ( /0 sweep angle of quarter chord Λ1 4 = 30 € 15 Subsonic Air Compressibility Effects on 3-D Wing Lift Slope Subsonic 3-D wing, sweep = 0 plot(pi A / (1+sqrt(1 + ((A / 2)^2) (1 - M^2))), A=1 to 20, M = 0 to 0.9) 31 Subsonic Air Compressibility Effects on 3-D Wing Lift Slope Subsonic 3-D wing, sweep = 60 plot(pi A / (1+sqrt(1 + (A ^2) (1 – 0.5 M^2))), A=1 to 20, M = 0 to 0.9) 32 16 Lift-Drag Polar for a Typical Bizjet • L/D = slope of line drawn from origin – Single maximum for a given polar – Two solutions for lower L/D (high and low airspeed) – Available L/D decreases with Mach number • Intercept for L/Dmax depends only on ε and zero-lift drag Note different scales for lift and drag 33 Wing Lift Slope at M = 1 Approximation for all wing planforms π AR # AR& C = = 2π % ( Lα 2 $ 4 ' 34 17 Supersonic Effects on Arbitrary Wing and Wing-Body Lift Slope • Impinging shock waves • Discrete areas with differing M and local pressure coefficients, cp • Areas change with α • No simple equations for lift slope m = tanγ tan µ Schlicting & Truckenbrodt, 1979 , sweep angles of shock and leading edge, from x axis 35 γ µ = Supersonic Compressibility Effects on Triangular Wing Lift Slope Supersonic delta (triangular) wing Supersonic leading edge Subsonic leading edge 4 2π 2 cot Λ C = CL = Lα α M 2 − 1 (π + λ) where λ = m(0.38 + 2.26m − 0.86m2 ) m = cot ΛLE cotσ sweep angle of leading edge, from y axis Λ LE = 36 18 Historical Factoid Fighter Jets of the 1950s: “Century Series” • Emphasis on supersonic speed McDonnell F-101 North American F-100 Convair F-102 Republic F-105 Lockheed F-104 37 Transonic Drag Rise and the Area Rule • Richard Whitcomb (NASA Langley) and Wallace Hayes (Princeton) • YF-102A (left) could not break speed of sound in level flight; F-102A (right) could 38 19 Transonic Drag Rise and the Area Rule Cross-sectional area of total configuration should gradually increase and decrease to minimize transonic drag Talay, NASA SP-367 Sears-Haack Body Area Rule http://en.wikipedia.org/wiki/Sears-Haack_body https://en.wikipedia.org/wiki/Area_rule 39 Secondary Wing Structures • Vortex generators, fences, vortilons, notched or dog-toothed wing leading edges – Boundary layer control – Maintain attached flow with increasing α – Avoid tip stall McDonnell-Douglas F-4 LTV F-8 Sukhoi Su-22 40 20 Leading-Edge Extensions • Strakes or leading edge extensions – Maintain lift at high α – Reduce c.p.
Load more

Recommended publications
  • Glossary Physics (I-Introduction)
    1 Glossary Physics (I-introduction) - Efficiency: The percent of the work put into a machine that is converted into useful work output; = work done / energy used [-]. = eta In machines: The work output of any machine cannot exceed the work input (<=100%); in an ideal machine, where no energy is transformed into heat: work(input) = work(output), =100%. Energy: The property of a system that enables it to do work. Conservation o. E.: Energy cannot be created or destroyed; it may be transformed from one form into another, but the total amount of energy never changes. Equilibrium: The state of an object when not acted upon by a net force or net torque; an object in equilibrium may be at rest or moving at uniform velocity - not accelerating. Mechanical E.: The state of an object or system of objects for which any impressed forces cancels to zero and no acceleration occurs. Dynamic E.: Object is moving without experiencing acceleration. Static E.: Object is at rest.F Force: The influence that can cause an object to be accelerated or retarded; is always in the direction of the net force, hence a vector quantity; the four elementary forces are: Electromagnetic F.: Is an attraction or repulsion G, gravit. const.6.672E-11[Nm2/kg2] between electric charges: d, distance [m] 2 2 2 2 F = 1/(40) (q1q2/d ) [(CC/m )(Nm /C )] = [N] m,M, mass [kg] Gravitational F.: Is a mutual attraction between all masses: q, charge [As] [C] 2 2 2 2 F = GmM/d [Nm /kg kg 1/m ] = [N] 0, dielectric constant Strong F.: (nuclear force) Acts within the nuclei of atoms: 8.854E-12 [C2/Nm2] [F/m] 2 2 2 2 2 F = 1/(40) (e /d ) [(CC/m )(Nm /C )] = [N] , 3.14 [-] Weak F.: Manifests itself in special reactions among elementary e, 1.60210 E-19 [As] [C] particles, such as the reaction that occur in radioactive decay.
    [Show full text]
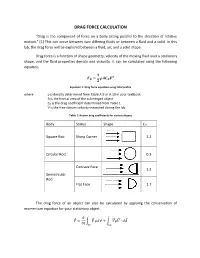
  • Drag Force Calculation
    DRAG FORCE CALCULATION “Drag is the component of force on a body acting parallel to the direction of relative motion.” [1] This can occur between two differing fluids or between a fluid and a solid. In this lab, the drag force will be explored between a fluid, air, and a solid shape. Drag force is a function of shape geometry, velocity of the moving fluid over a stationary shape, and the fluid properties density and viscosity. It can be calculated using the following equation, ퟏ 푭 = 흆푨푪 푽ퟐ 푫 ퟐ 푫 Equation 1: Drag force equation using total profile where ρ is density determined from Table A.9 or A.10 in your textbook A is the frontal area of the submerged object CD is the drag coefficient determined from Table 1 V is the free-stream velocity measured during the lab Table 1: Known drag coefficients for various shapes Body Status Shape CD Square Rod Sharp Corner 2.2 Circular Rod 0.3 Concave Face 1.2 Semicircular Rod Flat Face 1.7 The drag force of an object can also be calculated by applying the conservation of momentum equation for your stationary object. 휕 퐹⃗ = ∫ 푉⃗⃗ 휌푑∀ + ∫ 푉⃗⃗휌푉⃗⃗ ∙ 푑퐴⃗ 휕푡 퐶푉 퐶푆 Assuming steady flow, the equation reduces to 퐹⃗ = ∫ 푉⃗⃗휌푉⃗⃗ ∙ 푑퐴⃗ 퐶푆 The following frontal view of the duct is shown below. Integrating the velocity profile after the shape will allow calculation of drag force per unit span. Figure 1: Velocity profile after an inserted shape. Combining the previous equation with Figure 1, the following equation is obtained: 푊 퐷푓 = ∫ 휌푈푖(푈∞ − 푈푖)퐿푑푦 0 Simplifying the equation, you get: 20 퐷푓 = 휌퐿 ∑ 푈푖(푈∞ − 푈푖)훥푦 푖=1 Equation 2: Drag force equation using wake profile The pressure measurements can be converted into velocity using the Bernoulli’s equation as follows: 2Δ푃푖 푈푖 = √ 휌퐴푖푟 Be sure to remember that the manometers used are in W.C.
    [Show full text]
  • Notes on Earth Atmospheric Entry for Mars Sample Return Missions
    NASA/TP–2006-213486 Notes on Earth Atmospheric Entry for Mars Sample Return Missions Thomas Rivell Ames Research Center, Moffett Field, California September 2006 The NASA STI Program Office . in Profile Since its founding, NASA has been dedicated to the • CONFERENCE PUBLICATION. Collected advancement of aeronautics and space science. The papers from scientific and technical confer- NASA Scientific and Technical Information (STI) ences, symposia, seminars, or other meetings Program Office plays a key part in helping NASA sponsored or cosponsored by NASA. maintain this important role. • SPECIAL PUBLICATION. Scientific, technical, The NASA STI Program Office is operated by or historical information from NASA programs, Langley Research Center, the Lead Center for projects, and missions, often concerned with NASA’s scientific and technical information. The subjects having substantial public interest. NASA STI Program Office provides access to the NASA STI Database, the largest collection of • TECHNICAL TRANSLATION. English- aeronautical and space science STI in the world. language translations of foreign scientific and The Program Office is also NASA’s institutional technical material pertinent to NASA’s mission. mechanism for disseminating the results of its research and development activities. These results Specialized services that complement the STI are published by NASA in the NASA STI Report Program Office’s diverse offerings include creating Series, which includes the following report types: custom thesauri, building customized databases, organizing and publishing research results . even • TECHNICAL PUBLICATION. Reports of providing videos. completed research or a major significant phase of research that present the results of NASA For more information about the NASA STI programs and include extensive data or theoreti- Program Office, see the following: cal analysis.
    [Show full text]
  • Enhancing General Aviation Aircraft Safety with Supplemental Angle of Attack Systems
    University of North Dakota UND Scholarly Commons Theses and Dissertations Theses, Dissertations, and Senior Projects January 2015 Enhancing General Aviation Aircraft aS fety With Supplemental Angle Of Attack Systems David E. Kugler Follow this and additional works at: https://commons.und.edu/theses Recommended Citation Kugler, David E., "Enhancing General Aviation Aircraft aS fety With Supplemental Angle Of Attack Systems" (2015). Theses and Dissertations. 1793. https://commons.und.edu/theses/1793 This Dissertation is brought to you for free and open access by the Theses, Dissertations, and Senior Projects at UND Scholarly Commons. It has been accepted for inclusion in Theses and Dissertations by an authorized administrator of UND Scholarly Commons. For more information, please contact [email protected]. ENHANCING GENERAL AVIATION AIRCRAFT SAFETY WITH SUPPLEMENTAL ANGLE OF ATTACK SYSTEMS by David E. Kugler Bachelor of Science, United States Air Force Academy, 1983 Master of Arts, University of North Dakota, 1991 Master of Science, University of North Dakota, 2011 A Dissertation Submitted to the Graduate Faculty of the University of North Dakota in partial fulfillment of the requirements for the degree of Doctor of Philosophy Grand Forks, North Dakota May 2015 Copyright 2015 David E. Kugler ii PERMISSION Title Enhancing General Aviation Aircraft Safety With Supplemental Angle of Attack Systems Department Aviation Degree Doctor of Philosophy In presenting this dissertation in partial fulfillment of the requirements for a graduate degree from the University of North Dakota, I agree that the library of this University shall make it freely available for inspection. I further agree that permission for extensive copying for scholarly purposes may be granted by the professor who supervised my dissertation work or, in his absence, by the Chairperson of the department or the dean of the School of Graduate Studies.
    [Show full text]
  • Sailing for Performance
    SD2706 Sailing for Performance Objective: Learn to calculate the performance of sailing boats Today: Sailplan aerodynamics Recap User input: Rig dimensions ‣ P,E,J,I,LPG,BAD Hull offset file Lines Processing Program, LPP: ‣ Example.bri LPP_for_VPP.m rigdata Hydrostatic calculations Loading condition ‣ GZdata,V,LOA,BMAX,KG,LCB, hulldata ‣ WK,LCG LCF,AWP,BWL,TC,CM,D,CP,LW, T,LCBfpp,LCFfpp Keel geometry ‣ TK,C Solve equilibrium State variables: Environmental variables: solve_Netwon.m iterative ‣ VS,HEEL ‣ TWS,TWA ‣ 2-dim Netwon-Raphson iterative method Hydrodynamics Aerodynamics calc_hydro.m calc_aero.m VS,HEEL dF,dM Canoe body viscous drag Lift ‣ RFC ‣ CL Residuals Viscous drag Residuary drag calc_residuals_Newton.m ‣ RR + dRRH ‣ CD ‣ dF = FAX + FHX (FORCE) Keel fin drag ‣ dM = MH + MR (MOMENT) Induced drag ‣ RF ‣ CDi Centre of effort Centre of effort ‣ CEH ‣ CEA FH,CEH FA,CEA The rig As we see it Sail plan ≈ Mainsail + Jib (or genoa) + Spinnaker The sail plan is defined by: IMSYC-66 P Mainsail hoist [m] P E Boom leech length [m] BAD Boom above deck [m] I I Height of fore triangle [m] J Base of fore triangle [m] LPG Perpendicular of jib [m] CEA CEA Centre of effort [m] R Reef factor [-] J E LPG BAD D Sailplan modelling What is the purpose of the sails on our yacht? To maximize boat speed on a given course in a given wind strength ‣ Max driving force, within our available righting moment Since: We seek: Fx (Thrust vs Resistance) ‣ Driving force, FAx Fy (Side forces, Sails vs. Keel) ‣ Heeling force, FAy (Mx (Heeling-righting moment)) ‣ Heeling arm, CAE Aerodynamics of sails A sail is: ‣ a foil with very small thickness and large camber, ‣ with flexible geometry, ‣ usually operating together with another sail ‣ and operating at a large variety of angles of attack ‣ Environment L D V Each vertical section is a differently cambered thin foil Aerodynamics of sails TWIST due to e.g.
    [Show full text]
  • Critical Mach Number, Transonic Area Rule
    Critical Mach number - Compressibility Effects on Lift The design parameter that influences compressibility effects on lift is the Critical Mach number (Mcr). This is the free stream Mach number when sonic conditions (M = 1) is reached at some point on the airfoil surface The figure illustrates the same airfoil, at the same angle of attack at different free stream Mach numbers leading to the definition of the critical Mach number The critical Mach number can be obtained through the curve for the minimum pressure coefficient as a function of Mach number. It can be determined through the intersection of the two equations The lift coefficient correction for compressibility is The figure above illustrates that If you plan to fly at high free stream Mach number, you airfoil should be thin to (a) increase your critical Mach number as this will keep your drag rise small This will also result in lower minimum pressure: Therefore your lift coefficient will decrease Note that the minimum pressure coefficient on thick airfoil is high; this means that the velocity is also correspondingly high. Therefore the critical Mach number is reached for lower value of the free stream Mach number. Swept wing A B-52 Stratofortress showing wing with a large sweepback angle. A swept wing is a wing planform favored for high subsonic jet speeds first investigated in Germany from 1935 onwards until the end of the Second World War. Since the introduction of the MiG-15 and North American F-86 which demonstrated a decisive superiority over the slower first generation of straight-wing jet fighters during the Korean War, swept wings have become almost universal on all but the slowest jets (such as the A- 10).
    [Show full text]
  • Conceptual Design Study of a Hydrogen Powered Ultra Large Cargo Aircraft
    Conceptual Design Study of a Hydrogen Powered Ultra Large Cargo Aircraft R.A.J. Jansen University of Technology Technology of University Delft Delft Conceptual Design Study of a Hydrogen Powered Ultra Large Cargo Aircraft Towards a competitive and sustainable alternative of maritime transport by R.A.J. Jansen to obtain the degree of Master of Science at the Delft University of Technology, to be defended publicly on Tuesday January 10, 2017 at 9:00 AM. Student number: 4036093 Thesis registration: 109#17#MT#FPP Project duration: January 11, 2016 – January 10, 2017 Thesis committee: Dr. ir. G. La Rocca, TU Delft, supervisor Dr. A. Gangoli Rao, TU Delft Dr. ir. H. G. Visser, TU Delft An electronic version of this thesis is available at http://repository.tudelft.nl/. Acknowledgements This report presents the research performed to complete the master track Flight Performance and Propulsion at the Technical University of Delft. I am really grateful to the people who supported me both during the master thesis as well as during the rest of my student life. First of all, I would like to thank my supervisor, Gianfranco La Rocca. He supported and motivated me during the entire graduation project and provided valuable feedback during all the status meeting we had. I would also like to thank the exam committee, Arvind Gangoli Rao and Dries Visser, for their flexibility and time to assess my work. Moreover, I would like to thank Ali Elham for his advice throughout the project as well as during the green light meeting. Next to these people, I owe also thanks to the fellow students in room 2.44 for both their advice, as well as the enjoyable chats during the lunch and coffee breaks.
    [Show full text]
  • Feeling Supersonic
    FlightGlobal.com May 2021 How Max cuts hurt Boeing backlog Making throwaway Feeling aircraft aff ordable p32 Hydrogen switch for Fresson’s Islander p34 supersonic Will Overture be in tune with demand? p52 9 770015 371327 £4.99 Big worries Warning sign We assess A380 Why NOTAM outlook as last burden can delivery looms baffl e pilots 05 p14 p22 Comment Prospects receding Future dreaming Once thought of as the future of air travel, the A380 is already heading into retirement, but aviation is keenly focused on the next big thing Airbus t has been a rapid rise and fall for on who you ask. As we report else- Hydrogen is not without its the Airbus A380, which not so where in this issue, there are those issues, of course, but nonethe- long ago was being hailed as the banking on supersonic speeds be- less it appears more feasible as a future of long-haul air travel. ing the answer. power source for large transport IThe superjumbo would be, The likes of Aerion and Boom Su- aircraft than batteries do at pres- forecasts said, the perfect tool for personic view the ability to shave ent, even allowing for improving airlines operating into mega-hubs significant time from journeys as a energy densities. such as Dubai that were beginning unique selling point. However, there are others who to spring up. While projects are likely to be see hydrogen through a differ- But the planners at Airbus failed technologically feasible, to be able ent filter. They argue that so- to take into consideration the to sell these new aircraft in signif- called sub-regional aircraft – the efficiency gains available from icant volumes their manufacturers Britten-Norman Islander, among a new generation of widebody will have to ensure that supersonic others – can be given fresh impetus twinjets that allowed operators to flight is not merely the domain of if a fuel source can be found that is open up previously uneconomical the ultra-rich.
    [Show full text]
  • Brazilian 14-Xs Hypersonic Unpowered Scramjet Aerospace Vehicle
    ISSN 2176-5480 22nd International Congress of Mechanical Engineering (COBEM 2013) November 3-7, 2013, Ribeirão Preto, SP, Brazil Copyright © 2013 by ABCM BRAZILIAN 14-X S HYPERSONIC UNPOWERED SCRAMJET AEROSPACE VEHICLE STRUCTURAL ANALYSIS AT MACH NUMBER 7 Álvaro Francisco Santos Pivetta Universidade do Vale do Paraíba/UNIVAP, Campus Urbanova Av. Shishima Hifumi, no 2911 Urbanova CEP. 12244-000 São José dos Campos, SP - Brasil [email protected] David Romanelli Pinto ETEP Faculdades, Av. Barão do Rio Branco, no 882 Jardim Esplanada CEP. 12.242-800 São José dos Campos, SP, Brasil [email protected] Giannino Ponchio Camillo Instituto de Estudos Avançados/IEAv - Trevo Coronel Aviador José Alberto Albano do Amarante, nº1 Putim CEP. 12.228-001 São José dos Campos, SP - Brasil. [email protected] Felipe Jean da Costa Instituto Tecnológico de Aeronáutica/ITA - Praça Marechal Eduardo Gomes, nº 50 Vila das Acácias CEP. 12.228-900 São José dos Campos, SP - Brasil [email protected] Paulo Gilberto de Paula Toro Instituto de Estudos Avançados/IEAv - Trevo Coronel Aviador José Alberto Albano do Amarante, nº1 Putim CEP. 12.228-001 São José dos Campos, SP - Brasil. [email protected] Abstract. The Brazilian VHA 14-X S is a technological demonstrator of a hypersonic airbreathing propulsion system based on supersonic combustion (scramjet) to fly at Earth’s atmosphere at 30km altitude at Mach number 7, designed at the Prof. Henry T. Nagamatsu Laboratory of Aerothermodynamics and Hypersonics, at the Institute for Advanced Studies. Basically, scramjet is a fully integrated airbreathing aeronautical engine that uses the oblique/conical shock waves generated during the hypersonic flight, to promote compression and deceleration of freestream atmospheric air at the inlet of the scramjet.
    [Show full text]
  • Effects of Gurney Flap on Supercritical and Natural Laminar Flow Transonic Aerofoil Performance
    Effects of Gurney Flap on Supercritical and Natural Laminar Flow Transonic Aerofoil Performance Ho Chun Raybin Yu March 2015 MPhil Thesis Department of Mechanical Engineering The University of Sheffield Project Supervisor: Prof N. Qin Thesis submitted to the University of Sheffield in partial fulfilment of the requirements for the degree of Master of Philosophy Abstract The aerodynamic effect of a novel combination of a Gurney flap and shockbump on RAE2822 supercritical aerofoil and RAE5243 Natural Laminar Flow (NLF) aerofoil is investigated by solving the two-dimensional steady Reynolds-averaged Navier-Stokes (RANS) equation. The shockbump geometry is predetermined and pre-optimised on a specific designed condition. This study investigated Gurney flap height range from 0.1% to 0.7% aerofoil chord length. The drag benefits of camber modification against a retrofit Gurney flap was also investigated. The results indicate that a Gurney flap has the ability to move shock downstream on both types of aerofoil. A significant lift-to-drag improvement is shown on the RAE2822, however, no improvement is illustrated on the RAE5243 NLF. The results suggest that a Gurney flap may lead to drag reduction in high lift regions, thus, increasing the lift-to-drag ratio before stall. Page 2 Dedication I dedicate this thesis to my beloved grandmother Sandy Yip who passed away during the course of my research, thank you so much for the support, I love you grandma. This difficult journey would not have completed without the deep understanding, support, motivation, encouragement and unconditional love from my beloved parents Maggie and James and my brother Billy.
    [Show full text]
  • Airframe Integration
    Aerodynamic Design of the Hybrid Wing Body Propulsion- Airframe Integration May-Fun Liou1, Hyoungjin Kim2, ByungJoon Lee3, and Meng-Sing Liou4 NASA Glenn Research Center, Cleveland, Ohio, 44135 Abstract A hybrid wingbody (HWB) concept is being considered by NASA as a potential subsonic transport aircraft that meets aerodynamic, fuel, emission, and noise goals in the time frame of the 2030s. While the concept promises advantages over conventional wing-and-tube aircraft, it poses unknowns and risks, thus requiring in-depth and broad assessments. Specifically, the configuration entails a tight integration of the airframe and propulsion geometries; the aerodynamic impact has to be carefully evaluated. With the propulsion nacelle installed on the (upper) body, the lift and drag are affected by the mutual interference effects between the airframe and nacelle. The static margin for longitudinal stability is also adversely changed. We develop a design approach in which the integrated geometry of airframe (HWB) and propulsion is accounted for simultaneously in a simple algebraic manner, via parameterization of the planform and airfoils at control sections of the wingbody. In this paper, we present the design of a 300-passenger transport that employs distributed electric fans for propulsion. The trim for stability is achieved through the use of the wingtip twist angle. The geometric shape variables are determined through the adjoint optimization method by minimizing the drag while subject to lift, pitch moment, and geometry constraints. The design results clearly show the influence on the aerodynamic characteristics of the installed nacelle and trimming for stability. A drag minimization with the trim constraint yields a reduction of 10 counts in the drag coefficient.
    [Show full text]
  • SBM20-322 2015 June 23 Temporary
    MOONEY INTERNATIONAL CORPORATION SERVICE BULLETIN 165 Al Mooney Road North Kerrville, Texas 78028 SERVICE BULLETIN M20-322 Date: June 23, 2015 THIS BULLETIN IS FAA APPROVED FOR ENGINEERING DESIGN SUBJECT: Temporary Replacement of Icing System Stall Strip MODELS/ SN Mooney Aircraft with Known Icing System Installed AFFECTED: TIME OF AS SOON AS PRACTICABLE COMPLIANCE: INTRODUCTION: For instances involving missing icing system stall strips, airplanes are grounded. To remedy this situation, a temporary non-icing system stall strip can be installed in place of the icing stall strip to allow the aircraft to operate as a “Not Certified for Flight in Known Icing Conditions” aircraft until the icing strip can be installed. This Service Bulletin is to provide instructions for installing the temporary stall strip. The attached compliance card needs to be filled out and returned to Mooney International Corporation upon completion of this Service Bulletin M20-322. WARNING: Flight into known icing conditions and the use of the aircraft’s icing system is prohibited until the permanent icing system stall strip can be installed. This Service Bulletin only allows for a temporary non-icing stall strip to be installed for temporary flight until the permanent icing stall strip can be obtained. INSTRUCTIONS: Read entire procedures before beginning work. INSTALLING TEMPORARY STALL STRIP: 1.1. Disable and secure circuit breaker to prevent accidental operation of icing system. 1.2. Remove all old sealant and thoroughly clean the porous surface of the wing where the temporary stall strip is to be installed. Acceptable cleaning solvents are listed below. NOTE: The primary factor affecting the adhesion of the stall strip is absolute cleanliness of the porous panel.
    [Show full text]