DOCSLIB.ORG

A Mollifier Approach to Regularize a Cauchy Problem for The

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Mollifier Approach to Regularize a Cauchy Problem for The A mollifier approach to regularize a Cauchy problem for the inhomogeneous Helmholtz equation Pierre MARECHAL´ ,∗ Walter Cedric SIMO TAO LEE,† Faouzi TRIKI‡ May 7, 2021 Abstract The Cauchy problem for the inhomogeneous Helmholtz equation with non-uniform refraction index is considered. The ill-posedness of this problem is tackled by means of the variational form of mollification. This approach is proved to be consistent, and the proposed numerical simulations are quite promising. 1 Introduction Let V be a C3;1 bounded domain of R3 with boundary @V . For x0 @V , we denote by ν(x0) the unit normal vector to @V pointing outward V . Let Γ be a nonempty2 open subset of @V . We consider the Cauchy problem for the inhomogeneous Helmholtz equation ∆u(x) + k2η(x)u(x) = S(x); x V; (1) 0 0 0 2 @νu(x ) = f(x ); x Γ; (2) 2 u(x0) = g(x0); x0 Γ: (3) 2 1 arXiv:2105.02665v1 [math.AP] 6 May 2021 Here, u = u(x) is the unknown amplitude of the incident field, η L (Ω) is the refraction index, k is a positive wave number, S L2(Ω) is the source function,2 and f L2(Γ) and 2 2 ∗Institut de Math´ematiques universit´e Paul Sabatier, 31062 Toulouse, France. Email: [email protected] †Institut de Math´ematiques universit´e Paul Sabatier, 31062 Toulouse, France. Email: wsimo- [email protected] ‡Laboratoire Jean Kuntzmann, UMR CNRS 5224, Universit´eGrenoble-Alpes, 700 Avenue Centrale, 38401 Saint-Martin-d'H`eres,France. Email: [email protected]. This work is supported in part by the grant ANR-17-CE40-0029 of the French National Research Agency ANR (project MultiOnde). 1 g L2(Γ) are empirically known boundary conditions. 2 The Helmholtz equation arises in a large range of applications related to the propagation of acoustic and electromagnetic waves in the time-harmonic regime. In this paper, we con- sider the inverse problem of reconstructing an acoustic or electromagnetic field from partial data given on an open part of the boundary of a given domain. This problem called the Cauchy problem for the Helmholtz equation is known to be ill-posed if Γ does not occupy the whole boundary @V [13,9, 18,1]. In [17], the above system was considered in the particular case where the refraction index is constant. However, in practice, the emitted wave travels through an environment in which the refraction index fails to be constant, and we need to investigate the corresponding problem. We are facing a linear inverse problem. Our aim is to derive a stable approximation method for this problem, which yields stable and amenable computational scheme. Our main focus will be on mollification, in the variational sense of the term, which turns out to be both flexible and numerically efficient. Mollifiers were introduced in partial differential equations by K.O. Friedrichs [27, 11]. The term mollification has been used in the field of inverse problems since the eighties. In the original works on the subject, mollifiers were used to smooth the data prior to inversion. In his book, D.A. Murio [23] provides an overview of this approach and its application to some classical inverse problems. Let us also mention the paper by D.N. Hao [14], which provides a wide framework for the mollification approach in this initial meaning. In [21], A.K. Louis and P. Maass proposed another approach, based on inner product duality. This approach has been subsequently referred to as the method of approximate inverses [24]. The approximate inverses are particularly well adapted to problems in which the adjoint equation has explicit solutions. A third approach, based on a variational formulation, also appeared in the same period of time. In [20], A. Lannes et al. gave such a formulation while studying the problems of Fourier extrapolation and deconvolution. This variational formulation was not studied further until the papers by N. Alibaud et al. [2] and by X. Bonnefond and P. Mar´echal [7], where convergence properties of the variational formulation was considered. A definite advantage of the variational approach to mollification lies in the fact that it offers a quite flexible framework, just like the Tikhonov regularization, while being more respectful of the initial model equation than the latter. The paper is organized as follows. In Section2, we introduce the linear operator associated to the Cauchy problem for the inhomogeneous Helmholtz equation. We propose a regularized variational formulation of the ill-posed problem based on mollification. Under an additional smoothness assumption on the targeted solution we show in Theorem7 that the unique min- imizer converges strongly to the minimum-norm least square solution. Section3 is devoted to numerical experiments. We consider two numerical examples in order to illustrate the efficiency of our regularization approach. 2 2 Functional setting and regularization We shall work in a functional space which enables us to interpret the ideal (exact) data as the image of u by a bounded linear operator. We observe that: (I) the Laplacian ∆ is a bounded operator from H2(V ) to L2(V ), so that, since η L1(Ω), 2 2 2 2 the operator T1u = (∆ + k η)u is also bounded from H (V ) to L (V )[12]; 1 3 1=2 (II) u (H (V )) , so that u @νu H (Γ) is a continuous linear operator, which r 2 7! 2 2 2 implies in turn that the operator T2u = @νujΓ is compact from H (V ) to L (Γ); 2 3=2 (III) the trace operator u uj@V maps H (V ) to H (Γ) continuously, so that the operator 7! 2 2 T3u = ujΓ is compact from H (V ) to L (Γ). Therefore, a natural choice for our workspace is H2(V ). We can then write our system in the form T u = v; (4) in which T : H2(V ) L2(V ) L2(Γ) L2(Γ) −! × × 2 u ∆u + k ηu; @νu; u 7−! and v = (S; f; g) G := L2(V ) L2(Γ) L2(Γ): 2 × × We first show that T is injective. Proposition 1. The linear bounded map T defined by (4) is injective. Proof. For a proof of this classical result, we refer to the Fritz John's book [19]. More recent proofs based on Carleman estimates can be found in [18,9,1, 26]. The principal idea is to show that a part of Γ is non-characteristic with respect to the Helmholtz operator, which in turns leads to the existence of a small neighborhood of that part of the boundary in V where 1 the solution is identically zero. Since η L (Ω), the Helmholtz operator T1 possesses the unique continuation property in V , and2 hence the solution is identically zero in the whole domain V which completes the proof. We are now going to set up our approach to the regularization of the problem. We consider the mollifier 1 x 3 'α(x) = ' ; α (0; 1]; x R ; α3 α 2 2 in which ' is an integrable function such that 3 (1) supp ' Br := x R x r for some positive r, ⊂ f 2 j k k ≤ g (2) R '(x) dx = 1. 3 Desirable additional properties of ' are, as usual, nonnegativity, isotropy, smoothness, radial decrease. 2 3 We denote by Cα the convolution operator by 'α: for every u L (R ), Cαu := 'α u. Our 2 ∗ regularization principle will control smoothness by means of Cα, and α will play the role of the regularization parameter. One difficulty lies in the fact that convolving u by 'α entails extrapolating u from V to the larger set V + αBr. Zero padding is obviously forbidden here since we wish to preserve H2 regularity. It is then necessary to introduce an extension operator that preserves the properties of the solution on V . 2+s R3 2+s R3 For s [0; 1), we denote by H0 ( ) the set of functions in H ( ) having a compact 2 2+s 2+s R3 support. Our objective is to derive an extension operator E : H (V ) H0 ( ) that in 2+s ! addition of satisfying Eu V = u for all u H (V ), is bounded and invertible. Note that there are many extensionj operators satisfying2 these properties. We next provide a complete characterization of a useful extension operator suited for C3;1 smooth bounded domains. For other extension operators on Sobolev spaces under weaker regularity assumptions on the domain V; see, for example, [10, 22,8, 25]. For " (0; 1) small enough define the tubular domains 2 ± 0 0 0 + V := x tν(x ):(x ; t) @V (0;") ; and V" := V @V V : (5) " f ± 2 × g [ [ " − We first notice that V" V V" for all " (0; 1). Due to the regularity of @V , the function defined by ⊂ ⊂ 2 φ(x0; t) = x0 tν(x0); (6) − is a C2;1-diffeomorphism from @V (0;") onto V − for " small enough. × " 2 2 Let u be fixed in H (V ). The first step is to construct an extension u" of u to H (V"=2). For α; β R, set 2 u~(x0 + tν(x0)) = αu(x0 tν(x0)) + βu(x0 2tν(x0)); for (x0; t) @V (0; "=2): (7) − − 2 × 2 2 + Since ν is a C vector field,u ~ lies in H (V" ), and verifies 0 0 0 0 0 u~(x ) = (α + β)u(x ); and @νu~(x ) = ( α 2β)@νu(x ); x @V: (8) − − 2 Let u" be defined by + u~(x); x V"=2; u"(x) = 2 (9) u(x); x V: 2 2 2 + By construction, we have u" H (V ) H (V ).
Load more

Recommended publications
  • Geometric Integration Theory Contents
    Steven G. Krantz Harold R. Parks Geometric Integration Theory Contents Preface v 1 Basics 1 1.1 Smooth Functions . 1 1.2Measures.............................. 6 1.2.1 Lebesgue Measure . 11 1.3Integration............................. 14 1.3.1 Measurable Functions . 14 1.3.2 The Integral . 17 1.3.3 Lebesgue Spaces . 23 1.3.4 Product Measures and the Fubini–Tonelli Theorem . 25 1.4 The Exterior Algebra . 27 1.5 The Hausdorff Distance and Steiner Symmetrization . 30 1.6 Borel and Suslin Sets . 41 2 Carath´eodory’s Construction and Lower-Dimensional Mea- sures 53 2.1 The Basic Definition . 53 2.1.1 Hausdorff Measure and Spherical Measure . 55 2.1.2 A Measure Based on Parallelepipeds . 57 2.1.3 Projections and Convexity . 57 2.1.4 Other Geometric Measures . 59 2.1.5 Summary . 61 2.2 The Densities of a Measure . 64 2.3 A One-Dimensional Example . 66 2.4 Carath´eodory’s Construction and Mappings . 67 2.5 The Concept of Hausdorff Dimension . 70 2.6 Some Cantor Set Examples . 73 i ii CONTENTS 2.6.1 Basic Examples . 73 2.6.2 Some Generalized Cantor Sets . 76 2.6.3 Cantor Sets in Higher Dimensions . 78 3 Invariant Measures and the Construction of Haar Measure 81 3.1 The Fundamental Theorem . 82 3.2 Haar Measure for the Orthogonal Group and the Grassmanian 90 3.2.1 Remarks on the Manifold Structure of G(N,M).... 94 4 Covering Theorems and the Differentiation of Integrals 97 4.1 Wiener’s Covering Lemma and its Variants .
    [Show full text]
  • On the Use of Discrete Fourier Transform for Solving Biperiodic Boundary Value Problem of Biharmonic Equation in the Unit Rectangle
    On the Use of Discrete Fourier Transform for Solving Biperiodic Boundary Value Problem of Biharmonic Equation in the Unit Rectangle Agah D. Garnadi 31 December 2017 Department of Mathematics, Faculty of Mathematics and Natural Sciences, Bogor Agricultural University Jl. Meranti, Kampus IPB Darmaga, Bogor, 16680 Indonesia Abstract This note is addressed to solving biperiodic boundary value prob- lem of biharmonic equation in the unit rectangle. First, we describe the necessary tools, which is discrete Fourier transform for one di- mensional periodic sequence, and then extended the results to 2- dimensional biperiodic sequence. Next, we use the discrete Fourier transform 2-dimensional biperiodic sequence to solve discretization of the biperiodic boundary value problem of Biharmonic Equation. MSC: 15A09; 35K35; 41A15; 41A29; 94A12. Key words: Biharmonic equation, biperiodic boundary value problem, discrete Fourier transform, Partial differential equations, Interpola- tion. 1 Introduction This note is an extension of a work by Henrici [2] on fast solver for Poisson equation to biperiodic boundary value problem of biharmonic equation. This 1 note is organized as follows, in the first part we address the tools needed to solve the problem, i.e. introducing discrete Fourier transform (DFT) follows Henrici's work [2]. The second part, we apply the tools already described in the first part to solve discretization of biperiodic boundary value problem of biharmonic equation in the unit rectangle. The need to solve discretization of biharmonic equation is motivated by its occurence in some applications such as elasticity and fluid flows [1, 4], and recently in image inpainting [3]. Note that the work of Henrici [2] on fast solver for biperiodic Poisson equation can be seen as solving harmonic inpainting.
    [Show full text]
  • Introduction to Sobolev Spaces
    Introduction to Sobolev Spaces Lecture Notes MM692 2018-2 Joa Weber UNICAMP December 23, 2018 Contents 1 Introduction1 1.1 Notation and conventions......................2 2 Lp-spaces5 2.1 Borel and Lebesgue measure space on Rn .............5 2.2 Definition...............................8 2.3 Basic properties............................ 11 3 Convolution 13 3.1 Convolution of functions....................... 13 3.2 Convolution of equivalence classes................. 15 3.3 Local Mollification.......................... 16 3.3.1 Locally integrable functions................. 16 3.3.2 Continuous functions..................... 17 3.4 Applications.............................. 18 4 Sobolev spaces 19 4.1 Weak derivatives of locally integrable functions.......... 19 1 4.1.1 The mother of all Sobolev spaces Lloc ........... 19 4.1.2 Examples........................... 20 4.1.3 ACL characterization.................... 21 4.1.4 Weak and partial derivatives................ 22 4.1.5 Approximation characterization............... 23 4.1.6 Bounded weakly differentiable means Lipschitz...... 24 4.1.7 Leibniz or product rule................... 24 4.1.8 Chain rule and change of coordinates............ 25 4.1.9 Equivalence classes of locally integrable functions..... 27 4.2 Definition and basic properties................... 27 4.2.1 The Sobolev spaces W k;p .................. 27 4.2.2 Difference quotient characterization of W 1;p ........ 29 k;p 4.2.3 The compact support Sobolev spaces W0 ........ 30 k;p 4.2.4 The local Sobolev spaces Wloc ............... 30 4.2.5 How the spaces relate.................... 31 4.2.6 Basic properties { products and coordinate change.... 31 i ii CONTENTS 5 Approximation and extension 33 5.1 Approximation............................ 33 5.1.1 Local approximation { any domain............. 33 5.1.2 Global approximation on bounded domains.......
    [Show full text]
  • Proving the Regularity of the Reduced Boundary of Perimeter Minimizing Sets with the De Giorgi Lemma
    PROVING THE REGULARITY OF THE REDUCED BOUNDARY OF PERIMETER MINIMIZING SETS WITH THE DE GIORGI LEMMA Presented by Antonio Farah In partial fulfillment of the requirements for graduation with the Dean's Scholars Honors Degree in Mathematics Honors, Department of Mathematics Dr. Stefania Patrizi, Supervising Professor Dr. David Rusin, Honors Advisor, Department of Mathematics THE UNIVERSITY OF TEXAS AT AUSTIN May 2020 Acknowledgements I deeply appreciate the continued guidance and support of Dr. Stefania Patrizi, who supervised the research and preparation of this Honors Thesis. Dr. Patrizi kindly dedicated numerous sessions to this project, motivating and expanding my learning. I also greatly appreciate the support of Dr. Irene Gamba and of Dr. Francesco Maggi on the project, who generously helped with their reading and support. Further, I am grateful to Dr. David Rusin, who also provided valuable help on this project in his role of Honors Advisor in the Department of Mathematics. Moreover, I would like to express my gratitude to the Department of Mathematics' Faculty and Administration, to the College of Natural Sciences' Administration, and to the Dean's Scholars Honors Program of The University of Texas at Austin for my educational experience. 1 Abstract The Plateau problem consists of finding the set that minimizes its perimeter among all sets of a certain volume. Such set is known as a minimal set, or perimeter minimizing set. The problem was considered intractable until the 1960's, when the development of geometric measure theory by researchers such as Fleming, Federer, and De Giorgi provided the necessary tools to find minimal sets.
    [Show full text]
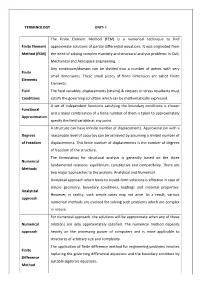
  • TERMINOLOGY UNIT- I Finite Element Method (FEM)
    TERMINOLOGY UNIT- I The Finite Element Method (FEM) is a numerical technique to find Finite Element approximate solutions of partial differential equations. It was originated from Method (FEM) the need of solving complex elasticity and structural analysis problems in Civil, Mechanical and Aerospace engineering. Any continuum/domain can be divided into a number of pieces with very Finite small dimensions. These small pieces of finite dimension are called Finite Elements Elements. Field The field variables, displacements (strains) & stresses or stress resultants must Conditions satisfy the governing condition which can be mathematically expressed. A set of independent functions satisfying the boundary conditions is chosen Functional and a linear combination of a finite number of them is taken to approximately Approximation specify the field variable at any point. A structure can have infinite number of displacements. Approximation with a Degrees reasonable level of accuracy can be achieved by assuming a limited number of of Freedom displacements. This finite number of displacements is the number of degrees of freedom of the structure. The formulation for structural analysis is generally based on the three Numerical fundamental relations: equilibrium, constitutive and compatibility. There are Methods two major approaches to the analysis: Analytical and Numerical. Analytical approach which leads to closed-form solutions is effective in case of simple geometry, boundary conditions, loadings and material properties. Analytical However, in reality, such simple cases may not arise. As a result, various approach numerical methods are evolved for solving such problems which are complex in nature. For numerical approach, the solutions will be approximate when any of these Numerical relations are only approximately satisfied.
    [Show full text]
  • Classics in Mathematics Richard Courant· Fritz John Introduction To
    Classics in Mathematics Richard Courant· Fritz John Introduction to Calculus and Analysis Volume I Springer-V erlag Berlin Heidelberg GmbH Richard Courant • Fritz John Introd uction to Calculus and Analysis Volume I Reprint of the 1989 Edition Springer Originally published in 1965 by Interscience Publishers, a division of John Wiley and Sons, Inc. Reprinted in 1989 by Springer-Verlag New York, Inc. Mathematics Subject Classification (1991): 26-XX, 26-01 Cataloging in Publication Data applied for Die Deutsche Bibliothek - CIP-Einheitsaufnahme Courant, Richard: Introduction to calcu1us and analysis / Richard Courant; Fritz John.- Reprint of the 1989 ed.- Berlin; Heidelberg; New York; Barcelona; Hong Kong; London; Milan; Paris; Singapore; Tokyo: Springer (Classics in mathematics) VoL 1 (1999) ISBN 978-3-540-65058-4 ISBN 978-3-642-58604-0 (eBook) DOI 10.1007/978-3-642-58604-0 Photograph of Richard Courant from: C. Reid, Courant in Gottingen and New York. The Story of an Improbable Mathematician, Springer New York, 1976 Photograph of Fritz John by kind permission of The Courant Institute of Mathematical Sciences, New York ISSN 1431-0821 This work is subject to copyright. All rights are reserved. whether the whole or part of the material is concemed. specifically the rights of trans1ation. reprinting. reuse of illustrations. recitation. broadcasting. reproduction on microfilm or in any other way. and storage in data banks. Duplication of this publication or parts thereof is permitted onlyunder the provisions of the German Copyright Law of September 9.1965. in its current version. and permission for use must always be obtained from Springer-Verlag. Violations are Iiable for prosecution under the German Copyright Law.
    [Show full text]
  • Lecture 7: the Complex Fourier Transform and the Discrete Fourier Transform (DFT)
    Lecture 7: The Complex Fourier Transform and the Discrete Fourier Transform (DFT) c Christopher S. Bretherton Winter 2014 7.1 Fourier analysis and filtering Many data analysis problems involve characterizing data sampled on a regular grid of points, e. g. a time series sampled at some rate, a 2D image made of regularly spaced pixels, or a 3D velocity field from a numerical simulation of fluid turbulence on a regular grid. Often, such problems involve characterizing, detecting, separating or ma- nipulating variability on different scales, e. g. finding a weak systematic signal amidst noise in a time series, edge sharpening in an image, or quantifying the energy of motion across the different sizes of turbulent eddies. Fourier analysis using the Discrete Fourier Transform (DFT) is a fun- damental tool for such problems. It transforms the gridded data into a linear combination of oscillations of different wavelengths. This partitions it into scales which can be separately analyzed and manipulated. The computational utility of Fourier methods rests on the Fast Fourier Transform (FFT) algorithm, developed in the 1960s by Cooley and Tukey, which allows efficient calculation of discrete Fourier coefficients of a periodic function sampled on a regular grid of 2p points (or 2p3q5r with slightly reduced efficiency). 7.2 Example of the FFT Using Matlab, take the FFT of the HW1 wave height time series (length 24 × 60=25325) and plot the result (Fig. 1): load hw1 dat; zhat = fft(z); plot(abs(zhat),’x’) A few elements (the second and last, and to a lesser extent the third and the second from last) have magnitudes that stand above the noise.
    [Show full text]
  • Discretization of Integro-Differential Equations
    Discretization of Integro-Differential Equations Modeling Dynamic Fractional Order Viscoelasticity K. Adolfsson1, M. Enelund1,S.Larsson2,andM.Racheva3 1 Dept. of Appl. Mech., Chalmers Univ. of Technology, SE–412 96 G¨oteborg, Sweden 2 Dept. of Mathematics, Chalmers Univ. of Technology, SE–412 96 G¨oteborg, Sweden 3 Dept. of Mathematics, Technical University of Gabrovo, 5300 Gabrovo, Bulgaria Abstract. We study a dynamic model for viscoelastic materials based on a constitutive equation of fractional order. This results in an integro- differential equation with a weakly singular convolution kernel. We dis- cretize in the spatial variable by a standard Galerkin finite element method. We prove stability and regularity estimates which show how the convolution term introduces dissipation into the equation of motion. These are then used to prove a priori error estimates. A numerical ex- periment is included. 1 Introduction Fractional order operators (integrals and derivatives) have proved to be very suit- able for modeling memory effects of various materials and systems of technical interest. In particular, they are very useful when modeling viscoelastic materials, see, e.g., [3]. Numerical methods for quasistatic viscoelasticity problems have been studied, e.g., in [2] and [8]. The drawback of the fractional order viscoelastic models is that the whole strain history must be saved and included in each time step. The most commonly used algorithms for this integration are based on the Lubich convolution quadrature [5] for fractional order operators. In [1, 2], we develop an efficient numerical algorithm based on sparse numerical quadrature earlier studied in [6]. While our earlier work focused on discretization in time for the quasistatic case, we now study space discretization for the fully dynamic equations of mo- tion, which take the form of an integro-differential equation with a weakly singu- lar convolution kernel.
    [Show full text]
  • L P and Sobolev Spaces
    NOTES ON Lp AND SOBOLEV SPACES STEVE SHKOLLER 1. Lp spaces 1.1. Definitions and basic properties. Definition 1.1. Let 0 < p < 1 and let (X; M; µ) denote a measure space. If f : X ! R is a measurable function, then we define 1 Z p p kfkLp(X) := jfj dx and kfkL1(X) := ess supx2X jf(x)j : X Note that kfkLp(X) may take the value 1. Definition 1.2. The space Lp(X) is the set p L (X) = ff : X ! R j kfkLp(X) < 1g : The space Lp(X) satisfies the following vector space properties: (1) For each α 2 R, if f 2 Lp(X) then αf 2 Lp(X); (2) If f; g 2 Lp(X), then jf + gjp ≤ 2p−1(jfjp + jgjp) ; so that f + g 2 Lp(X). (3) The triangle inequality is valid if p ≥ 1. The most interesting cases are p = 1; 2; 1, while all of the Lp arise often in nonlinear estimates. Definition 1.3. The space lp, called \little Lp", will be useful when we introduce Sobolev spaces on the torus and the Fourier series. For 1 ≤ p < 1, we set ( 1 ) p 1 X p l = fxngn=1 j jxnj < 1 : n=1 1.2. Basic inequalities. Lemma 1.4. For λ 2 (0; 1), xλ ≤ (1 − λ) + λx. Proof. Set f(x) = (1 − λ) + λx − xλ; hence, f 0(x) = λ − λxλ−1 = 0 if and only if λ(1 − xλ−1) = 0 so that x = 1 is the critical point of f. In particular, the minimum occurs at x = 1 with value f(1) = 0 ≤ (1 − λ) + λx − xλ : Lemma 1.5.
    [Show full text]
  • Fritz John, 1910–1994 an Elegant Construction of the Fundamental Solution for Par- Fritz John Died in New Rochelle, NY, on February 10, 1994
    people.qxp 3/16/99 5:26 PM Page 255 Mathematics People Mathematics of the AMS and the Society for Industrial and Moser Receives Wolf Prize Applied Mathematics (1968), the Craig Watson Medal of Jürgen Moser of the Eidgenössische Technische Hochschule the U.S. National Academy of Sciences (1969), the John von in Zürich will receive the 1994–1995 Wolf Prize in Mathe- Neumann Lectureship of SIAM (1984), the L. E. J. Brouwer matics. The noted German mathematician will be honored Medal (1984), an Honorary Professorship at the Instituto with the $100,000 award by the Israel-based Wolf Foun- de Matematica Pura e Applicada (1989), and an honorary dation for his “fundamental work on stability in Hamil- doctorate from the University of Bochum (1990). Moser is tonian mechanics and his profound and influential con- a member of the U.S. National Academy of Sciences. tributions to nonlinear differential equations.” The 1994–1995 Wolf Prizes will be presented in March —from Wolf Foundation News Release by the president of Israel, Ezer Weizman, at the Knesset (Parliament) building in Jerusalem. A total of $600,000 will be awarded for outstanding achievements in the fields Aisenstadt Prizes Announced of agriculture, chemistry, physics, medicine, the arts, and mathematics. The Wolf Foundation was established by the The Centre de Recherches Mathématiques in Montreal has late Ricardo Wolf, an inventor, diplomat, and philanthropist. announced that the third and fourth André Aisenstadt Among Moser’s most important achievements is his Mathematics Prizes have been awarded to Nigel D. Hig- role in the development of KAM (Kolmogorov-Arnold- son of Pennsylvania State University and Michael J.
    [Show full text]
  • There Is Only One Fourier Transform Jens V
    Preprints (www.preprints.org) | NOT PEER-REVIEWED | Posted: 25 December 2017 doi:10.20944/preprints201712.0173.v1 There is only one Fourier Transform Jens V. Fischer * Microwaves and Radar Institute, German Aerospace Center (DLR), Germany Abstract Four Fourier transforms are usually defined, the Integral Fourier transform, the Discrete-Time Fourier transform (DTFT), the Discrete Fourier transform (DFT) and the Integral Fourier transform for periodic functions. However, starting from their definitions, we show that all four Fourier transforms can be reduced to actually only one Fourier transform, the Fourier transform in the distributional sense. Keywords Integral Fourier Transform, Discrete-Time Fourier Transform (DTFT), Discrete Fourier Transform (DFT), Integral Fourier Transform for periodic functions, Fourier series, Poisson Summation Formula, periodization trick, interpolation trick Introduction Two Important Operations The fact that “there is only one Fourier transform” actually There are two operations which are being strongly related to needs no proof. It is commonly known and often discussed in four different variants of the Fourier transform, i.e., the literature, for example in [1-2]. discretization and periodization. For any real-valued T > 0 and δ(t) being the Dirac impulse, let However frequently asked questions are: (1) What is the difference between calculating the Fourier series and the (1) Fourier transform of a continuous function? (2) What is the difference between Discrete-Time Fourier Transform (DTFT) be the function that results from a discretization of f(t) and let and Discrete Fourier Transform (DFT)? (3) When do we need which Fourier transform? and many others. The default answer (2) today to all these questions is to invite the reader to have a look at the so-called Fourier-Poisson cube, e.g.
    [Show full text]
  • Optimal Filter and Mollifier for Piecewise Smooth Spectral Data
    MATHEMATICS OF COMPUTATION Volume 75, Number 254, Pages 767–790 S 0025-5718(06)01822-9 Article electronically published on January 23, 2006 OPTIMAL FILTER AND MOLLIFIER FOR PIECEWISE SMOOTH SPECTRAL DATA JARED TANNER This paper is dedicated to Eitan Tadmor for his direction Abstract. We discuss the reconstruction of piecewise smooth data from its (pseudo-) spectral information. Spectral projections enjoy superior resolution provided the function is globally smooth, while the presence of jump disconti- nuities is responsible for spurious O(1) Gibbs’ oscillations in the neighborhood of edges and an overall deterioration of the convergence rate to the unaccept- able first order. Classical filters and mollifiers are constructed to have compact support in the Fourier (frequency) and physical (time) spaces respectively, and are dilated by the projection order or the width of the smooth region to main- tain this compact support in the appropriate region. Here we construct a noncompactly supported filter and mollifier with optimal joint time-frequency localization for a given number of vanishing moments, resulting in a new fun- damental dilation relationship that adaptively links the time and frequency domains. Not giving preference to either space allows for a more balanced error decomposition, which when minimized yields an optimal filter and mol- lifier that retain the robustness of classical filters, yet obtain true exponential accuracy. 1. Introduction The Fourier projection of a 2π periodic function π ˆ ikx ˆ 1 −ikx (1.1) SN f(x):= fke , fk := f(x)e dx, 2π − |k|≤N π enjoys the well-known spectral convergence rate, that is, the convergence rate is as rapid as the global smoothness of f(·) permits.
    [Show full text]