Overview of Japan Standard Time Generation
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

English Edition of Mayors for Peace News Flash
April 2021 / No.136 Check our website and follow us on SNS: Mayors for Peace Member Cities Website http://www.mayorsforpeace.org/english/index.html 8,024 cities Facebook in 165 countries and regions https://www.facebook.com/mayorsforpeace Twitter (as of April 1, 2021) https://twitter.com/Mayors4Peace Help us achieve 10,000 member cities! “Like” and share our Facebook and Twitter posts to help spread awareness of our mission. Table of Contents ➢ 10th General Conference is rescheduled for August 2022 ➢ Invitation for the Children’s Art Competition “Peaceful Towns” 2021 ➢ Request for Payment of the 2021 Mayors for Peace Membership Fee ➢ Member city activities ➢ Regional chapter activities ➢ Mayors for Peace Member Cities - 8,024 cities in 165 countries/regions ➢ Reports by Executive Advisors ➢ ➢ Call for input: examples of initiatives to foster peace-seeking spirit ➢ Peace news from Hiroshima (provided by the Hiroshima Peace Media Center of the CHUGOKU SHIMBUN) ----------------------------------------------------------------------------------------- 10th General Conference is rescheduled for August 2022 ----------------------------------------------------------------------------------------- Mayors for Peace has been making arrangements to hold its 10th General Conference in Hiroshima this August, after our decision of postponing it from August 2020. However, even today, the world is yet to see clear signs of an end to the COVID-19 pandemic. Amidst such a situation, it would be very difficult to hold such a large-scale conference hosting attendees from all over the world, while preventing the spread of infection at the same time. In addition, some member cities outside of Japan have mentioned to the Secretariat that they are unlikely to be able to travel to Hiroshima to attend the General Conference due to financial constraints their cities are facing―reallocating and securing budget for medical support and economic recovery, while confronting decrease in tax revenues. -

Report of Time and Frequency Activities at NICT
CCTF/12-07 Report of Time and Frequency Activities at NICT National Institute of Information and Communications Technology Koganei, Tokyo, Japan 1. Introduction The National Institute of Information and Communications Technology (NICT), an incorporated administrative agency, was established in 2004 with its large part inherited from the Communications Research Laboratory (CRL). The activity of time and frequency standards is conducted within the Space-Time Standards Laboratory of the Applied Electromagnetic Research Institute, this group itself comprises of four groups as follows. Firstly, the Atomic Frequency Standards Group develops atomic clocks ranging in frequencies from microwave to the optical region. Specifically, Cs fountain primary frequency standards, a single Ca+ ion trap optical clock and a Sr optical lattice clock are originally developed. In addition, research in THz frequency standards has recently begun. The second group is the Japan Standard Time Group, which is responsible for generation of Japan Standard Time, its dissemination, and a frequency calibration service as a national authority. Thirdly, the Space-Time Measurement Group at Koganei develops precise time and frequency transfer techniques using optical fiber and satellite links. Lastly, the Space-Time Measurement Group at Kashima specializes in VLBI research using a 34 m antenna, and has recently begun research into VLBI precision time transfer. Details of these activities are described in the following sections. 2. Primary clocks NICT has been developing Cs atomic fountain frequency standards for contribution to the determination of TAI, and are also used in frequency calibration of Japan standard time and calibration of optical frequency standards. The first fountain (NICT-CsF1) has been in operation since 2006 and accuracy evaluations with CsF1 have been carried out a few times per year. -

Japan Standard Time Service Group
Space-Time Standards Laboratory Japan Standard Time 6HUYLFHGroup National Institute of Information and Communications Technology -DSDQ6WDQGDUG7LPH6HUYLFH*URXSʊ*HQHUDWLRQ&RPSDULVRQDQG 'LVVHPLQDWLRQRI-DSDQ6WDQGDUG7LPHDQG)UHTXHQF\6WDQGDUGV National Institute of Information and Communications Technology 7KH1DWLRQDO,QVWLWXWHRI,QIRUPDWLRQDQG&RPPXQLFDWLRQV7HFKQRORJ\ 1,&7 LVUHVSRQVLEOHIRUWKHLPSRUWDQW WDVNV RI *HQHUDWLRQ &RPSDULVRQ DQG 'LVVHPLQDWLRQ RI -DSDQ 6WDQGDUG 7LPH DQG )UHTXHQF\ 6WDQGDUGV ZKLFKKDYHDGLUHFWLPSDFWRQSHRSOH¶VOLYHV,QWKLVEURFKXUHZHILUVWH[SODLQKRZ,QWHUQDWLRQDO$WRPLF7LPH DQG &RRUGLQDWHG 8QLYHUVDO 7LPH DUH FDOFXODWHG :H WKHQ ORRN DW KRZ WKH VWDQGDUG WLPH DOO RYHU WKH ZRUOG LQFOXGLQJ -DSDQ 6WDQGDUG 7LPH LV JHQHUDWHG EDVHG RQ WKHP )LQDOO\ ZH LQWURGXFH WKUHH PDMRU IXQFWLRQV RI WKH-DSDQ6WDQGDUG7LPH6HUYLFH*URXS*HQHUDWLRQ&RPSDULVRQDQG'LVVHPLQDWLRQRI-DSDQ6WDQGDUG7LPH 6OJWFSTBM 5JNF 65 BU PO +BOVBSZ BOE UIF UXP IBWF TJODF ESJGUFE BQBSU 5"* JT EFDJEFE CZ DBMDVMBUJOH B XFJHIUFEBWFSBHFUJNFPGBUPNJDDMPDLTBSPVOEUIFXPSME PPSEJOBUFE6OJWFSTBM5JNFBOE-FBQ4FDPOE$ڦ "EKVTUNFOU 8IBUJTUIF5JNF 0VSEBJMZMJWFTBSFHPWFSOFECZUIFBQQBSFOUNPUJPOPGUIF4VO 4JODF UIF UJNF TDBMF VTFE JO NFBTVSJOH UJNF JT BUPNJD UJNF UIFSFJTBOFFEGPSBOBUPNJDUJNFUIBUJTDMPTFUP6OJWFSTBM5JNF 65 5IJTBUPNJDUJNFJTDBMMFE$PPSEJOBUFE6OJWFSTBM5JNF 65$ "T UIF BOHVMBS WFMPDJUZ PG UIF &BSUI JT BGGFDUFE CZ OBUVSBM QIFOPNFOBTVDIBTUJEBMGSJDUJPO UIFNBOUMF BOEUIFBUNPT B UJNF EJGGFSFODF CFUXFFO 65 BOE 65$ JT GMVDUVBUFE FGJOJUJPOPGB4FDPOE QIFSF% ڦ 5IFSFGPSF UP LFFQ UIF UJNF EJGGFSFODF CFUXFFO 65$ -

Program (Listed in Japan Standard Time)
Program (Listed in Japan Standard Time) Virtual Meeting (Zoom Video Webinar) from Osaka, Japan NOTE It is listed in Japan standard time. Please note the time difference. DATE Japan (JST), Seoul (KST) November 3rd (Tue) 08:30-18:00 Taiwan (CST=JST-1) November 3rd (Tue) 07:30-17:00 Europe (CET=JST-8h) November 3rd (Mon) 00:30-10:00 London (GMT=JST-9h) November 2nd (Mon) 23:30- November 3rd 09:00 NY (EST=JST-14h) November 2nd (Mon) 18:30- November 3rd 04:00 Denver (MST=JST-16h) November 2nd (Mon) 16:30- November 3rd 02:00 SF (PST=JST-17h) November 2nd (Mon) 15:30- November 3rd 01:00 (Day light saving time will end at 02:00 on November 1 PDT in USA, and 03:00 October 25 CEST) 08:30-08:35 Opening Remark Yoshikazu Inoue (National Hospital Organization Kinki-Chuo Chest Medical Center, Japan) 08:35-09:35 Sponsored Morning Session Sponsored by KONICA MINOLTA JAPAN, INC Dynamic X-ray (DXR) Can Change Imaging Diagnosis Chair : Hiroto Hatabu (Brigham and Women’s Hospital, USA) • Expectation for Chest Dynamic X-ray (DXR) Shoji Kudoh (Japan Anti-Tuberculosis Association, Nippon Medical School, Japan) • Clinical Applications of Chest Dynamic X-ray (DXR) Tomoyuki Hida (Kyushu University, Japan) 09:35-09:38 Break 09:38-10:28 SessionⅠ: Symposium: Interstitial Lung Abnormality (ILA) Chair : Hiroto Hatabu (Brigham and Women’s Hospital, USA), David Lynch (National Jewish Health, USA) 09:38-09:53 Introduction, Background, Definition (From the First Fleischner Webinar) Hiroto Hatabu (Brigham and Women’s Hospital, USA) 09:53-10:03 Radiologic Aspect (What Is ILA -

Information for Participants 49Th Session of the IPCC Kyoto, Japan
Information for participants 49th Session of the IPCC Kyoto, Japan May 8th to 12th, 2019 I. INTRODUCTION The forty-ninth Session of the Intergovernmental Panel on Climate Change (IPCC) will take place at the Kyoto International Conference Center, in the city of Kyoto, Japan from May 8th to 12th, 2019. The registration of participants to this meeting will open on May 7th 2019 from 16:00 – 18:00, May 8th 2019 from 8:00 – 18:00 and 9:00 – 16:00 from May 9th to 12th, 2019. Kyoto city is the former Imperial capital of Japan for more than one thousand years. Throughout the year, Kyoto is full of cultural, artistic, and nature related events. There are many cultural sites that are part of the World Heritage. Please visit https://kyoto.travel/en for more information. NOTE – This guide will provide participants attending the above mentioned IPCC meetings in Kyoto with useful information. Participants are advised to read it carefully and contact the IPCC Secretariat in case of questions. II. VISITORS TO KYOTO 1. International Airports Participants are recommended to arrive at the Kansai International Airport (KIX), where the major airlines operate daily flights as destination. 2. Time Zone Kyoto is in Japan Standard Time (JST). The JST is 9 hours ahead Greenwich Mean Time (GMT+9). There is no daylight-saving time system in Japan. 3. How to request a visa As of November 2018, Japan has taken measures concerning the Visa Exemption Arrangements for ordinary passport holders and for Diplomatic/Official passport holders with 68 countries/regions and 46 countries, respectively. -

Regional High-Level Summit for University Presidents And
E OSAKA SCHOOL OF NATIONAL CENTER FOR JAPAN PATENT OFFICE INTERNATIONAL PUBLIC INDUSTRIAL PROPERTY POLICY, OSAKA INFORMATION AND UNIVERSITY TRAINING, KANSAI OFFICE (INPIT-KANSAI) REGIONAL CONFERENCE WIPO/HL/IP/OSA/19/INF/2 ORIGINAL: ENGLISH DATE: NOVEMBER 15, 2019 Regional High-Level Summit for University Presidents and Senior Policy Makers on Creating an Enabling Innovation Environment (EIE) for Intellectual Property and Technology organized by the World Intellectual Property Organization (WIPO) in cooperation with Osaka School of International Public Policy (OSIPP), Osaka University, Japan; and The National Center for Industrial Property Information and Training, KANSAI office (INPIT-KANSAI) with the assistance of the Japan Patent Office (JPO) Osaka, November 25 to 27, 2019 GENERAL INFORMATION NOTE prepared by the International Bureau of WIPO 1. ORGANIZATION OF THE MEETING AND RELATED ACTIVITIES EVENT The Regional High-Level Summit for University Presidents and Senior Policy Makers on Creating an Enabling Innovation Environment (EIE) for Intellectual Property and Technology will be held on November 25 to 27, 2019, in Osaka, Japan. It is being organized by the World Intellectual Property Organization (WIPO) in cooperation with Osaka School of International Public Policy (OSIPP), Osaka University and the National Center for Industrial Property Information and Training, KANSAI office (INPIT-KANSAI), and with the assistance of the Japan Patent Office (JPO). OBJECTIVES The purpose of the EIE Summit, will be to discuss the value of supporting Intellectual Property (IP)-based technology transfer (TT) at many levels within the IP ecosystem of a country. Those attending the Summit come from the partner countries of the EIE Project for IP and Technology, namely from Malaysia, the Philippines, Sri Lanka, Thailand and Viet Nam. -

The Fukushima Daiichi Accident Technical Volume 4
The Fukushima Daiichi Accident Fukushima The The Fukushima Daiichi Accident Technical Volume 4/5 Technical Volume 4/5 Radiological Consequences Radiological Consequences Radiological PO Box 100, Vienna International Centre 1400 Vienna, Austria Printed in Austria ISBN 978–92–0–107015–9 (set) 1 THE FUKUSHIMA DAIICHI ACCIDENT TECHNICAL VOLUME 4 RADIOLOGICAL CONSEQUENCES The following States are Members of the International Atomic Energy Agency: AFGHANISTAN GERMANY OMAN ALBANIA GHANA PAKISTAN ALGERIA GREECE PALAU ANGOLA GUATEMALA PANAMA ARGENTINA GUYANA PAPUA NEW GUINEA ARMENIA HAITI PARAGUAY AUSTRALIA HOLY SEE PERU AUSTRIA HONDURAS PHILIPPINES AZERBAIJAN HUNGARY POLAND BAHAMAS ICELAND PORTUGAL BAHRAIN INDIA QATAR BANGLADESH INDONESIA REPUBLIC OF MOLDOVA BELARUS IRAN, ISLAMIC REPUBLIC OF ROMANIA BELGIUM IRAQ RUSSIAN FEDERATION BELIZE IRELAND RWANDA BENIN ISRAEL SAN MARINO BOLIVIA, PLURINATIONAL ITALY SAUDI ARABIA STATE OF JAMAICA SENEGAL BOSNIA AND HERZEGOVINA JAPAN SERBIA BOTSWANA JORDAN SEYCHELLES BRAZIL KAZAKHSTAN SIERRA LEONE BRUNEI DARUSSALAM KENYA SINGAPORE BULGARIA KOREA, REPUBLIC OF SLOVAKIA BURKINA FASO KUWAIT SLOVENIA BURUNDI KYRGYZSTAN SOUTH AFRICA CAMBODIA LAO PEOPLE’S DEMOCRATIC SPAIN CAMEROON REPUBLIC SRI LANKA CANADA LATVIA SUDAN CENTRAL AFRICAN LEBANON SWAZILAND REPUBLIC LESOTHO SWEDEN CHAD LIBERIA SWITZERLAND CHILE LIBYA SYRIAN ARAB REPUBLIC CHINA LIECHTENSTEIN TAJIKISTAN COLOMBIA LITHUANIA CONGO LUXEMBOURG THAILAND COSTA RICA MADAGASCAR THE FORMER YUGOSLAV CÔTE D’IVOIRE MALAWI REPUBLIC OF MACEDONIA CROATIA MALAYSIA TOGO -

JST-ERATO YAMAUCHI Materials Space-Tectonics Project ~ Towards Game-Changing Science and Engineering for Future~
Kickoff Conference: JST-ERATO YAMAUCHI Materials Space-Tectonics Project ~ Towards Game-Changing Science and Engineering for Future~ Organized by the JST-ERATO Yamauchi Materials Space-Tectonics Project Co-Organized by Japan Science and Technology Agency (JST), National Institute for Materials Science (NIMS), Waseda University, and The University of Queensland (UQ) Place (Simultaneous Broadcast): Research and Development Building (Building No.121), Waseda University / 1F, AIBN Building, UQ Online participation: ZOOM (You may know the link after your registration). Registration Fee: Free Registration: Please send your information (name, position, affiliation, e-mail address) to the ERATO- Office ([email protected]). Date: 17 April 2021 Time: 13:00 – 17:30 (Japan Standard Time) / 14:00 – 18:30 (Brisbane Time, Australia) Language: English [1] Opening Remarks (20 min) Chair: JST Time: 13:00 – 13:20 (Japan Standard Time) / 14:00 – 14:20 (Brisbane Time, Australia) • JST Representative (To be announced) • Professor Kazuhiro Hono (Vice-President, NIMS) • Professor Alan E Rowan (Director, Australian Institute for Bioengineering and Nanotechnology (AIBN), UQ) • Professor Hironori Kasahara (Senior Executive Vice President, Waseda University) [2] Outline of the JST-EARTO Yamauchi Materials Space-Tectonics (20 min) Chair: JST Time: 13:20 – 13:40 (Japan Standard Time) / 14:20 – 14:40 (Brisbane Time, Australia) • Professor Yusuke Yamauchi (Professor, UQ / Group Leader, NIMS / Visiting Professor, Waseda University) Break (10 min) [3] Plenary Lectures (45 min x 2 = 90 min) Time: 13:50 - 15:20 (Japan Standard Time) / 14:50 – 16:20 (Brisbane Time, Australia) • Professor Takuzo Aida (The University of Tokyo, Japan) Chair: Toru Asahi “Supramolecular Polymerization: Its Significance and Applications” • Professor Thomas E. -
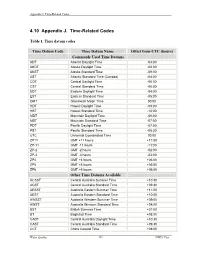
4.10 Appendix J. Time-Related Codes
Appendix J. Time-Related Codes 4.10 Appendix J. Time-Related Codes Table 1. Time datum codes Time Datum Code Time Datum Name Offset from UTC (hours) Commonly Used Time Datums ADT Atlantic Daylight Time -03:00 AKDT Alaska Daylight Time -08:00 AKST Alaska Standard Time -09:00 AST Atlantic Standard Time (Canada) -04:00 CDT Central Daylight Time -05:00 CST Central Standard Time -06:00 EDT Eastern Daylight Time -04:00 EST Eastern Standard Time -05:00 GMT Greenwich Mean Time 00:00 HDT Hawaii Daylight Time -09:00 HST Hawaii Standard Time -10:00 MDT Mountain Daylight Time -06:00 MST Mountain Standard Time -07:00 PDT Pacific Daylight Time -07:00 PST Pacific Standard Time -08:00 UTC Universal Coordinated Time 00:00 ZP11 GMT +11 hours +11:00 ZP-11 GMT -11 hours -11:00 ZP-2 GMT -2 hours -02:00 ZP-3 GMT -3 hours -03:00 ZP4 GMT +4 hours +04:00 ZP5 GMT +5 hours +05:00 ZP6 GMT +6 hours +06:00 Other Time Datums Available ACSST Central Australia Summer Time +10:30 ACST Central Australia Standard Time +09:30 AESST Australia Eastern Summer Time +11:00 AEST Australia Eastern Standard Time +10:00 AWSST Australia Western Summer Time +09:00 AWST Australia Western Standard Time +08:00 BST British Summer Time +01:00 BT Baghdad Time +03:00 CADT Central Australia Daylight Time +10:30 CAST Central Australia Standard Time +09:30 CCT China Coastal Time +08:00 Water Quality 336 NWIS User Appendix J. Time-Related Codes Table 1. -

5-2 Generating and Measurement System for Japan Standard Time
5-2 Generating and Measurement System for Japan Standard Time HANADO Yuko, IMAE Michito, KURIHARA Noriyuki, HOSOKAWA Mizuhiko, AIDA Masanori, IMAMURA Kuniyasu, KOTAKE Noboru, ITO Hiroyuki, SUZUYAMA Tomonari, NAKAGAWA Fumimaru, and SHIMIZU Yoshiyuki This article introduces the current and future systems for the standard time generating and measurement system at the CRL. The features of these current working systems com- pared with the former ones are dual redundancy in the main part. It is effective to improve reliable and rapid reaction to emergency situations. We are going to move the system to a new building next year and renew the current system on this opportunity. The new system will have many improvements such as an introduction of a hydrogen maser or multi-channel DMTD system, which enables it to realize a higher performance. Keywords UTC (Coordinated Universal Time), JST (Japan Standard Time), Measurement system, Hydrogen maser, DMTD (Dual Mixer Time Difference System) 1 Introduction tion, and time, once output, cannot be correct- ed. In other words, an abnormality cannot be Japan Standard Time (JST) is defined as corrected tracing it back to its occurrence. Coordinated Universal Time (UTC) + 9 hours. Therefore, in the construction of the system, The BIPM (Bureau International des Poids et the reliability of the system and the ease of Mesures) determines UTC from an ensemble long-term operation are as important as the of atomic clocks throughout the world, but system's main functions. In fact, the system UTC is not delivered to each country in real may on occasion be constructed to favor relia- time. -

Fukushima Daiichi Accident
The Fukushima Daiichi Accident Daiichi Fukushima The The Fukushima Daiichi Accident Report by the Director General the Director by Report Report by the Director General PO Box 100, Vienna International Centre 1400 Vienna, Austria Printed in Austria GC(59)/14 ISBN 978–92–0–107015–9 (set) 1 THE FUKUSHIMA DAIICHI ACCIDENT REPORT BY THE DIRECTOR GENERAL The following States are Members of the International Atomic Energy Agency: AFGHANISTAN GERMANY OMAN ALBANIA GHANA PAKISTAN ALGERIA GREECE PALAU ANGOLA GUATEMALA PANAMA ARGENTINA GUYANA PAPUA NEW GUINEA ARMENIA HAITI PARAGUAY AUSTRALIA HOLY SEE PERU AUSTRIA HONDURAS PHILIPPINES AZERBAIJAN HUNGARY POLAND BAHAMAS ICELAND PORTUGAL BAHRAIN INDIA QATAR BANGLADESH INDONESIA REPUBLIC OF MOLDOVA BELARUS IRAN, ISLAMIC REPUBLIC OF ROMANIA BELGIUM IRAQ RUSSIAN FEDERATION BELIZE IRELAND RWANDA BENIN ISRAEL SAN MARINO BOLIVIA, PLURINATIONAL ITALY SAUDI ARABIA STATE OF JAMAICA SENEGAL BOSNIA AND HERZEGOVINA JAPAN SERBIA BOTSWANA JORDAN SEYCHELLES BRAZIL KAZAKHSTAN SIERRA LEONE BRUNEI DARUSSALAM KENYA SINGAPORE BULGARIA KOREA, REPUBLIC OF SLOVAKIA BURKINA FASO KUWAIT SLOVENIA BURUNDI KYRGYZSTAN SOUTH AFRICA CAMBODIA LAO PEOPLE’S DEMOCRATIC SPAIN CAMEROON REPUBLIC SRI LANKA CANADA LATVIA SUDAN CENTRAL AFRICAN LEBANON SWAZILAND REPUBLIC LESOTHO SWEDEN CHAD LIBERIA SWITZERLAND CHILE LIBYA SYRIAN ARAB REPUBLIC CHINA LIECHTENSTEIN TAJIKISTAN COLOMBIA LITHUANIA CONGO LUXEMBOURG THAILAND COSTA RICA MADAGASCAR THE FORMER YUGOSLAV CÔTE D’IVOIRE MALAWI REPUBLIC OF MACEDONIA CROATIA MALAYSIA TOGO CUBA MALI TRINIDAD -
Application Guidelines for October 2021 Enrollment
Application Guidelines for October 2021 Enrollment KYOTO UNIVERSITY International Undergraduate Program (Kyoto iUP) Contents 1. Program Overview ...................................................................................................... 1 2. Eligibility Requirements ............................................................................................. 4 3. Admission Process ...................................................................................................... 5 4. Application and Enrollment Schedule ....................................................................... 6 5. Application Fee ............................................................................................................ 7 6. Application Documents ................................................................................................ 8 7. Qualifying Tests .......................................................................................................... 12 8. Scholarships and Support .......................................................................................... 12 9. Other Matters ............................................................................................................. 12 10. Contact Information ................................................................................................... 13 Appendix 1 (List of Acceptable Standardized Tests) ............................................... 14 Appendix 2 (Documents to be Submitted by March 12) ........................................