DOCSLIB.ORG

Extra-Solar Planets

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Extra-Solar Planets Stability Dynamics Habitability of Planets in Binary Systems Facts and Questions: Binary and Multi-Star Systems in the Solar neighbourhood: >60% Do the gravitational perturbations allow planetary formation ? (about 60 binary systems hosting planets) Information about the area of formation Long-term stability is of great interest search for habitable planets Outline Types of planetary motion in binary star systems Stability of planetary motion Examples of planetary motion in tight binaries Habitable planets in binaries? Solar System in a wide binary (Innanen et al. 1997) S-Typ Planetary motion in binaries: Trojans – type motion Near L4 and L5 L4 and L5 (stable for µ < 1:25) are at the third vertex of an equilateral triangle (Sun-Jupiter-Asteroid) Studies by : Harrington (1977) Graziani & Black (1981) and Black (1982) planar case: No serious threat to the long-term stability if the star is at a distance > 5 x planetary distance inclined case: at high iBinary the planetary orbits becomes unstable Kozai mechanism Pendleton & Black (1983) Some General Numerical Studies of planetary motion in binary systems: Dvorak R.(1984 and 1986) Rabl & Dvorak R. (1988) Dvorak R., Froeschle C. & Froeschle Ch. (1989) Holman M. & Wiegert P. (1999) Pilat-Lohinger E. & Dvorak R. (2002) Szenkovits F. & Mako Z. (2008) Stability analysis Initial Conditions: abinary =1 AU ebinary=[0, ….0.9] aplanet=[0.1, …0.9] eplanet=[0,… 0.9] i, Ώ,ω, = 0° M= 0°,90°,180°,270° Numerical Methods: Chaos Indicators: Long-term numerical Fast Lyapunov Indicator integration: (FLI) C. Froeschle, R.Gonczi, E. Lega Stability-Criterion: (1996) No close encounters within the Hill‘ sphere MEGNO RLI (i)Escape time Helicity Angle (ii) Study of the eccentricity: maximum eccentricity Lyapunov Exponent General Studies of S-type motion in binary systems: Dvorak R.(1984 and 1986) Rabl & Dvorak R. (1988) Dvorak R., Froeschle C. & Froeschle Ch. (1989) (200-500 periods) Holman M. & Wiegert P. (1999) (mass-ratios: 0.1-09, eBinary: 0 – 0.9; 10000 periods) Pilat-Lohinger & Dvorak (2002): The Fast Lyapunov Indicator (FLI) (see Froeschle et al., CMDA 1997) distinguish between regular and chaotic motion ; length of the largest tangent vector: FLI(t) = sup_i |v_i(t)| i=1,.....,n (n denotes the dimension of the phase space) chaotic orbits can be found very quickly because of the exponential growth of this vector in the chaotic region; For most chaotic orbits only a few number of primary revolutions is needed to determine the orbital behavior. Stability analysis Initial Conditions: abinary =1 AU ebinary=[0, ….0.9] aplanet=[0.1, …0.9] eplanet=[0,… 0.9] i, Ώ,ω, = 0° M= 0°,90°,180°,270° mass-ratio = 0.5 S-type motion mass-ratio e_binary 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 0.0 0.45 0.38 0.37 0.30 0.26 0.23 0.20 0.16 0.13 0.1 0.37 0.32 0.29 0.27 0.24 0.20 0.18 0.15 0.11 0.2 0.32 0.27 0.25 0.22 0.19 0.18 0.16 0.13 0.10 0.3 0.28 0.24 0.21 0.18 0.16 0.15 0.13 0.11 0.09 0.4 0.21 0.20 0.18 0.16 0.15 0.12 0.11 0.10 0.07 0.5 0.17 0.16 0.13 0.12 0.12 0.09 0.09 0.07 0.06 0.6 0.13 0.12 0.11 0.10 0.08 0.08 0.07 0.06 0.045 0.7 0.09 0.08 0.07 0.07 0.05 0.05 0.05 0.045 0.035 0.8 0.05 0.05 0.04 0.04 0.03 0.035 0.03 0.025 0.02 Stable zone (in units of length) of S-type motion for all computed mass-ratios and eccentricities of the binary. The given size for each (mu,e_binary) pair is the lower value of the studies by Holman &Wiegert (AJ,1999) and Pilat-Lohinger &Dvorak (CMDA, 2002) planets in binaries tight binary systems binary abinary [AU] ebinary M1/M2 Gliese86 22 ? 0.7/0.5 γ Cephei 20 0.44 1.6/0.4 HD41004 23 ? 0.7/0.4 HD188753 12.3 0.5 1.06/1.63 HD196885 25 ? 1.3/0.6 Examples of Planets in Tight Binary Systems: binary abinary [AU] ebinary m1 m2 [mSun] Gliese86 ~22 ? 0.7 0.5 γ Cephei ~20 0.4 1.6 0.4 HD41004 ~23 ? 0.7 0.4 Gliese86 γ Cephei HD 41004 m sin i = 2.3 MJ m sin i = 1.6 MJ m sin i = 4 MJ a = 1.3 AU ( 1.6 or 1.7) a = 2.15 AU a = 0.11AU e = 0.39 +/- 0.17 ? e = 0.045 e = 0.11 – 0.2 Influence of the eccentricity of the planet? Influence of the eccentricity mass-ratio = 0.2 γ Cephei : a_binary= 20 AU e_binary= 0.44 e_planet= 0.2 acrit = 0.18 SZ= 3.6 AU a_planet=2.15 AU Pilat-Lohinger & Dvorak, (CeMDA 2002) The mass of the planet ? Is the elliptic restricted three body problem a good model ? Circular Planetary Motion: -- Size of Stable Region RTP 1Jup 3Jup 5Jup e_bin 0 0.38 0.38 0.35 0.35 0.1 0.34 0.31 0.31 0.31 0.2 0. 30 0.24 0.24 0.24 0.3 0.24 0.21 0.21 0.21 0.4 0. 20 0.20 0.20 0.20 0.5 0.16 0.14 0.14 0.14 Elliptic Planetary Motion: e_bin 0.1 0.2 0.3 0.4 0.5 e_plan 0.0 0.31 0.24 0.22 0.21 0.14 0.1 0.31 0.24 0.22 0.19 0.14 0.2 0.28 0.24 0.18 0.16 0.14 0.3 0.26 0.24 0.19 0.15 0.13 0.4 0.25 0.21 0.16 0.13 0.11 0.5 0.19 0.16 0.14 0.12 0.09 Stable Region for a 5Jupiter-mass Planet e_bin=0.4 RTBP 1Mj 3Mj 5Mj 8Mj e_plan 0.0 0.2 0 0.20 0.20 0.20 0.20 0.1 0.2 0 0.20 0.20 0.19 0.19 0.2 0.18 0.18 0.17 0.16 016 0.3 0.17 0.16 0.16 0.15 0.15 0.4 0.17 0.15 0.14 0.13 0.13 0.5 0.15 0.12 0.11 0.09 0.09 gamma Cephei a_bin ~ 20 AU, e_bin ~ 0.4 RTBP 1Mj 3Mj 5Mj 8Mj e_plan 0.0 4.0 4.0 4.0 4.0 4.0 0.1 4.0 4.0 4.0 3.8 3.8 0.2 3.8 3.6 3.4 3.2 3.2 0.3 3.4 3.6 3.2 3.0 3.0 0.4 3.4 3.0 2.8 2.6 2.6 0.5 3.0 2.4 2.2 1.8 1.8 mass-ratio = 0.2 γ Cephei a_bin = 22 AU e_bin = 0.44 3.6AU a_p = 2 AU e_p=0.21 a_bin=18.5AU e_bin=0.36 3.2 AU a_p=2.13AU e_p=0.12 Stability limits mass-ratio border of stable motion Gamma Cephei: 0.2 3.2 – 3.8 AU HD41004 AB: 0.36 (e=0.39) 4.6 – 2.8 AU (e=0.5) 4.6 – 2.53AU Gliese 86: 0.42 close-in planet γ Cephei mass-ratio = 0.2 aBinary = 20 AU eBinary ~ 0.4 increase e γ Cep b : 0.11 0.5. Planet’s eccentricity border of stable region [AU] 0.0 4.0 0.1 3.8 0.2 3.6 0.3 3.4 04 3.2 0.5 3.0 gamma Cephei eBinary not known ! binary abinary [AU] ebinary m1 m2 Gliese86 ~22 ? 0.7 0.5 γ Cephei ~20 0.4 1.6 0.4 HD41004 ~23 ? 0.7 0.4 HD 41004A: m sin i = 2.3 MJ a = 1.3 AU ( 1.6 or 1.7) e = 0.39 +/- 0.17 ? HD41004 AB Influence of the secondary on the planetary motion ? with without secondary secondary gammaCep e_b=0.44 e_pl=0.209 HD41004 e_b=0.2 e_pl=0.22 Differences of the two planetary systems: semi-major axis of the planet eccentricity of the binary mass-ratio of the binary mass of the giant planet different e_binary different mass-ratio Gamma Cephei Planet is close to the host-star: The region is mainly influenced by the mean motion resonances If the planet is closer to the secondary -> an arc-like structure of chaos appears which depends on: a_planet, e_binary, masses, Habitable Zone Zone around a star where liquid water can exist on the surface of a terrestial-like planet This zone depends on: the spectraltype , the mass , the age, …. of the star the orbit of the planet the mass, the composition, the atmosphere , ……of the planet the parameters of other planets in this system (mass, orbit, …) The Habitable Zone based on the definition given by Kasting et al. (1993). Different HZs Binary Star Configurations: Different Binary Configurations Insolation Next Studies: Inclined planetary systems Results for HD41004A stable motion in the HZ only for a < 0.7 AU the eccentricity of the binary ebin < 0.7 we have found two zones for habitable planets: for nearly circular planetary motion around 0.5 AU the eccentricity of the detected planet has to be < 0.36 for higher eccentric efpl < 0.06 e < 0.23 planetary motion around fpl 0.6 AU the eccentricity of the maximum eccentricity detected planet has to be < 0.3 gamma Cephei Primary and Secondary: m1 = 1.6 MS m2 = 0.4 MS a = 20AU e = 0.44 Planet: mP = 1.7 Mjup a = 2.15 AU e = 0.2 Gliese 86 aBinary=22 AU eBinary=0.7 HZ of HD41004 A red: low ecc.
Load more

Recommended publications
  • Where Are the Distant Worlds? Star Maps
    W here Are the Distant Worlds? Star Maps Abo ut the Activity Whe re are the distant worlds in the night sky? Use a star map to find constellations and to identify stars with extrasolar planets. (Northern Hemisphere only, naked eye) Topics Covered • How to find Constellations • Where we have found planets around other stars Participants Adults, teens, families with children 8 years and up If a school/youth group, 10 years and older 1 to 4 participants per map Materials Needed Location and Timing • Current month's Star Map for the Use this activity at a star party on a public (included) dark, clear night. Timing depends only • At least one set Planetary on how long you want to observe. Postcards with Key (included) • A small (red) flashlight • (Optional) Print list of Visible Stars with Planets (included) Included in This Packet Page Detailed Activity Description 2 Helpful Hints 4 Background Information 5 Planetary Postcards 7 Key Planetary Postcards 9 Star Maps 20 Visible Stars With Planets 33 © 2008 Astronomical Society of the Pacific www.astrosociety.org Copies for educational purposes are permitted. Additional astronomy activities can be found here: http://nightsky.jpl.nasa.gov Detailed Activity Description Leader’s Role Participants’ Roles (Anticipated) Introduction: To Ask: Who has heard that scientists have found planets around stars other than our own Sun? How many of these stars might you think have been found? Anyone ever see a star that has planets around it? (our own Sun, some may know of other stars) We can’t see the planets around other stars, but we can see the star.
    [Show full text]
  • Stability of Planets in Binary Star Systems
    StabilityStability ofof PlanetsPlanets inin BinaryBinary StarStar SystemsSystems Ákos Bazsó in collaboration with: E. Pilat-Lohinger, D. Bancelin, B. Funk ADG Group Outline Exoplanets in multiple star systems Secular perturbation theory Application: tight binary systems Summary + Outlook About NFN sub-project SP8 “Binary Star Systems and Habitability” Stand-alone project “Exoplanets: Architecture, Evolution and Habitability” Basic dynamical types S-type motion (“satellite”) around one star P-type motion (“planetary”) around both stars Image: R. Schwarz Exoplanets in multiple star systems Observations: (Schwarz 2014, Binary Catalogue) ● 55 binary star systems with 81 planets ● 43 S-type + 12 P-type systems ● 10 multiple star systems with 10 planets Example: γ Cep (Hatzes et al. 2003) ● RV measurements since 1981 ● Indication for a “planet” (Campbell et al. 1988) ● Binary period ~57 yrs, planet period ~2.5 yrs Multiplicity of stars ~45% of solar like stars (F6 – K3) with d < 25 pc in multiple star systems (Raghavan et al. 2010) Known exoplanet host stars: single double triple+ source 77% 20% 3% Raghavan et al. (2006) 83% 15% 2% Mugrauer & Neuhäuser (2009) 88% 10% 2% Roell et al. (2012) Exoplanet catalogues The Extrasolar Planets Encyclopaedia http://exoplanet.eu Exoplanet Orbit Database http://exoplanets.org Open Exoplanet Catalogue http://www.openexoplanetcatalogue.com The Planetary Habitability Laboratory http://phl.upr.edu/home NASA Exoplanet Archive http://exoplanetarchive.ipac.caltech.edu Binary Catalogue of Exoplanets http://www.univie.ac.at/adg/schwarz/multiple.html Habitable Zone Gallery http://www.hzgallery.org Binary Catalogue Binary Catalogue of Exoplanets http://www.univie.ac.at/adg/schwarz/multiple.html Dynamical stability Stability limit for S-type planets Rabl & Dvorak (1988), Holman & Wiegert (1999), Pilat-Lohinger & Dvorak (2002) Parameters (a , e , μ) bin bin Outer limit at roughly max.
    [Show full text]
  • Can There Be Additional Rocky Planets in the Habitable Zone of Tight Binary
    Mon. Not. R. Astron. Soc. 000, 1–10 () Printed 24 September 2018 (MN LATEX style file v2.2) Can there be additional rocky planets in the Habitable Zone of tight binary stars with a known gas giant? B. Funk1⋆, E. Pilat-Lohinger1 and S. Eggl2 1Institute for Astronomy, University of Vienna, Vienna, Austria 2IMCCE, Observatoire de Paris, Paris, France ABSTRACT Locating planets in Habitable Zones (HZs) around other stars is a growing field in contem- porary astronomy. Since a large percentage of all G-M stars in the solar neighborhood are expected to be part of binary or multiple stellar systems, investigations of whether habitable planets are likely to be discovered in such environments are of prime interest to the scientific community. As current exoplanet statistics predicts that the chances are higher to find new worlds in systems that are already known to have planets, we examine four known extrasolar planetary systems in tight binaries in order to determine their capacity to host additional hab- itable terrestrial planets. Those systems are Gliese 86, γ Cephei, HD 41004 and HD 196885. In the case of γ Cephei, our results suggest that only the M dwarf companion could host ad- ditional potentially habitable worlds. Neither could we identify stable, potentially habitable regions around HD 196885A. HD 196885 B can be considered a slightly more promising tar- get in the search forEarth-twins.Gliese 86 A turned out to be a very good candidate, assuming that the system’s history has not been excessively violent. For HD 41004 we have identified admissible stable orbits for habitable planets, but those strongly depend on the parameters of the system.
    [Show full text]
  • On the Detection of Exoplanets Via Radial Velocity Doppler Spectroscopy
    The Downtown Review Volume 1 Issue 1 Article 6 January 2015 On the Detection of Exoplanets via Radial Velocity Doppler Spectroscopy Joseph P. Glaser Cleveland State University Follow this and additional works at: https://engagedscholarship.csuohio.edu/tdr Part of the Astrophysics and Astronomy Commons How does access to this work benefit ou?y Let us know! Recommended Citation Glaser, Joseph P.. "On the Detection of Exoplanets via Radial Velocity Doppler Spectroscopy." The Downtown Review. Vol. 1. Iss. 1 (2015) . Available at: https://engagedscholarship.csuohio.edu/tdr/vol1/iss1/6 This Article is brought to you for free and open access by the Student Scholarship at EngagedScholarship@CSU. It has been accepted for inclusion in The Downtown Review by an authorized editor of EngagedScholarship@CSU. For more information, please contact [email protected]. Glaser: Detection of Exoplanets 1 Introduction to Exoplanets For centuries, some of humanity’s greatest minds have pondered over the possibility of other worlds orbiting the uncountable number of stars that exist in the visible universe. The seeds for eventual scientific speculation on the possibility of these "exoplanets" began with the works of a 16th century philosopher, Giordano Bruno. In his modernly celebrated work, On the Infinite Universe & Worlds, Bruno states: "This space we declare to be infinite (...) In it are an infinity of worlds of the same kind as our own." By the time of the European Scientific Revolution, Isaac Newton grew fond of the idea and wrote in his Principia: "If the fixed stars are the centers of similar systems [when compared to the solar system], they will all be constructed according to a similar design and subject to the dominion of One." Due to limitations on observational equipment, the field of exoplanetary systems existed primarily in theory until the late 1980s.
    [Show full text]
  • Sulfur Hazes in Giant Exoplanet Atmospheres: Impacts on Reflected
    Draft version February 28, 2017 Preprint typeset using LATEX style AASTeX6 v. 1.0 SULFUR HAZES IN GIANT EXOPLANET ATMOSPHERES: IMPACTS ON REFLECTED LIGHT SPECTRA Peter Gao1,2,3, Mark S. Marley, and Kevin Zahnle NASA Ames Research Center Moffett Field, CA 94035, USA Tyler D. Robinson4,5 Department of Astronomy and Astrophysics University of California Santa Cruz Santa Cruz, CA 95064, USA Nikole K. Lewis Space Telescope Science Institute Baltimore, MD 21218, USA 1Division of Geological and Planetary Sciences, California Institute of Technology, Pasadena, CA 91125, USA 2NASA Postdoctoral Program Fellow [email protected] 4Sagan Fellow 5NASA Astrobiology Institute’s Virtual Planetary Laboratory ABSTRACT Recent work has shown that sulfur hazes may arise in the atmospheres of some giant exoplanets due to the photolysis of H2S. We investigate the impact such a haze would have on an exoplanet’s geometric albedo spectrum and how it may affect the direct imaging results of WFIRST, a planned NASA space telescope. For temperate (250 K < Teq < 700 K) Jupiter–mass planets, photochemical destruction of H2S results in the production of 1 ppmv of S8 between 100 and 0.1 mbar, which, if cool enough, ∼ will condense to form a haze. Nominal haze masses are found to drastically alter a planet’s geometric albedo spectrum: whereas a clear atmosphere is dark at wavelengths between 0.5 and 1 µm due to molecular absorption, the addition of a sulfur haze boosts the albedo there to 0.7 due to scattering. ∼ Strong absorption by the haze shortward of 0.4 µm results in albedos <0.1, in contrast to the high albedos produced by Rayleigh scattering in a clear atmosphere.
    [Show full text]
  • Star Festival 2016 Parade & Exhibition
    Jump!Star Festival 2016 Parade & Exhibition Images from George Ferrandi’s Wherever There is Water light parade for Fleisher Art Memorial 202.234.7103 Capitol Skyline Hotel [email protected] 10 I (Eye) Street SW www.wpadc.org Washington, DC 20024 TABLE OF CONTENTS INTRODUCTION Jump!Star Festival Concept History of the Project Festival Narrative Artist’s Biography COMPONENTS Community Engagement Workshops Light Exhibition Parade/Festival Images from George Ferrandi’s Wherever There is Water light parade for Fleisher Art Memorial INTRODUCTION Images from George Ferrandi’s Wherever There is Water light parade for Fleisher Art Memorial The Jump!Star Festival is a participatory public art project created by artist George Ferrandi that will celebrate the temporal nature of our pole star, the “North Star,” by bringing the local community together with a light parade, music, food, and a culminating exhibition of light sculptures created by local artists. Key Dates Parade/Festival: September 24, 2016 Workshops: May/June/July/August 2016 Exhibition: September 20-25, 2016 History of the Project For the Northern Hemisphere, Polaris, or the “North Star” is the guiding light for 90% of the world’s population, yet this Pole Star, the anchor of our heavens, is not permanent. Because the earth rotates at a slight angle on its axis, there is a slight shift in its rotation so that what we consider our “North Star” changes every few thousand years. When the pyramids were built, for example, there was a different “North Star” reigning over the heavens. Very few realize that our quintessential point of reference and ever reliable, literal “Guiding Light” is a temporary gig.
    [Show full text]
  • Analog SFF, April 2010 by Dell Magazine Authors
    Analog SFF, April 2010 by Dell Magazine Authors Dell Magazines www.analogsf.com Copyright ©2010 by Dell Magazines NOTICE: This eBook is licensed to the original purchaser only. Duplication or distribution to any person via email, floppy disk, network, print out, or any other means is a violation of International copyright law and subjects the violator to severe fines and/or imprisonment. This notice overrides the Adobe Reader permissions which are erroneous. This eBook cannot be legally lent or given to others. This eBook is displayed using 100% recycled electrons. 2 Analog SFF, April 2010 by Dell Magazine Authors Cover art by David A. Hardy Cover design by Victoria Green 3 Analog SFF, April 2010 by Dell Magazine Authors CONTENTS Reader's Department: EDITORIAL: THE REST OF THE DATA by Stanley Schmidt Department: BIOLOG: BRENDA COOPER by Richard A. Lovett Novelette: SWORDS AND SADDLES by John G. Hemry Science Fact: WHAT'S IN A KISS?: THE WILD, WONDERFUL WORLD OF PHILEMATOLOG by Richard A. Lovett Reader's Department: IN TIMES TO COME Novelette: SNOWFLAKE KISSES by Holly Hight & Richard A. Lovett Novelette: A SOUND BASIS FOR MISUNDERSTANDING by Carl Frederick Reader's Department: THE ALTERNATE VIEW: TAKEN ON FAITH by Jeffery D. Kooistra Novelette: NOTHIN' BUT BLUE SKIES by Stephen L. Burns Novelette: WHEN WE WERE FAB by Jerry Oltion Novelette: THE PLANET HUNTERS by S.L. Nickerson Novelette: THE ROBOTS' GIRL by Brenda Cooper Reader's Department: THE REFERENCE LIBRARY by Don Sakers Reader's Department: BRASS TACKS Reader's Department: UPCOMING EVENTS by Anthony Lewis * * * * 4 Analog SFF, April 2010 by Dell Magazine Authors Vol.
    [Show full text]
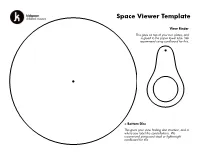
  • Space Viewer Template
    Space Viewer Template View Finder This goes on top of your two plates, and is glued to the paper towel tube. We recommend using cardboard for this. < Bottom Disc This gives your view finding disc structure, and is where you label the constellations. We recommend using card stock or lightweight cardboard for this. Constellation Plate > This disc is home to your constellations, and gets glued to the larger disc. We recommend using paper for this, so the holes are easier to punch. Use the punch guides on the next page to punch holes and add labels to your viewer. Orion Cancer Look for the middle star of Orions When you look at this constellation, look sword, that is an area of brighter nearby for 55 Cancri a star that has light, it’s actually a nebula! The five exoplanets orbiting it. One of those Orion Nebula is a gigantic cloud of plants (55 Cancri e) is a super hot dust and gas, where new stars are planet entirely covered in an ocean of being created. lava! Cygnus Andromeda This constellation is home to the This constellation is very close to the Kepler-186 system, including the Andromeda Galaxy (an enormous planet Kepler-186f. Seen by collection of gas, dust, and billions of NASA's Kepler Space Telescope, stars and solar systems). This spiral this is the first Earth-sized planet galaxy is so bright, you can spot it with discovered that is in"habitable the naked eye! zone" of its star. Ursa Minor Cassiopeia Ursa Minor has two stars known While gazing at Cassiopeia look for with exoplanets orbiting them - the“Pacman Nebula” (It’s official name both are gas giants, that are much is NGC 281).
    [Show full text]
  • Thursday, December 22Nd Swap Meet & Potluck Get-Together Next First
    Io – December 2011 p.1 IO - December 2011 Issue 2011-12 PO Box 7264 Eugene Astronomical Society Annual Club Dues $25 Springfield, OR 97475 President: Sam Pitts - 688-7330 www.eugeneastro.org Secretary: Jerry Oltion - 343-4758 Additional Board members: EAS is a proud member of: Jacob Strandlien, Tony Dandurand, John Loper. Next Meeting: Thursday, December 22nd Swap Meet & Potluck Get-Together Our December meeting will be a chance to visit and share a potluck dinner with fellow amateur astronomers, plus swap extra gear for new and exciting equipment from somebody else’s stash. Bring some food to share and any astronomy gear you’d like to sell, trade, or give away. We will have on hand some of the gear that was donated to the club this summer, including mirrors, lenses, blanks, telescope parts, and even entire telescopes. Come check out the bargains and visit with your fellow amateur astronomers in a relaxed evening before Christmas. We also encourage people to bring any new gear or projects they would like to show the rest of the club. The meeting is at 7:00 on December 22nd at EWEB’s Community Room, 500 E. 4th in Eugene. Next First Quarter Fridays: December 2nd and 30th Our November star party was clouded out, along with a good deal of the month afterward. If that sounds familiar, that’s because it is: I changed the date in the previous sentence from October to November and left the rest of the sentence intact. Yes, our autumn weather is predictable. Here’s hoping for a lucky break in the weather for our two December star parties.
    [Show full text]
  • Who Really Discovered the First Exoplanet?
    Who Really Discovered the First Exoplanet? Two Swiss astronomers got a well-deserved Nobel for finding an exoplanet, but there’s an intriguing backstory By Josh Winn The year 1995, like 1492, was the dawn of an age of discovery. The new explorers, instead of using seagoing vessels to discover continents, use telescopes to discover planets revolving around distant stars. Thousands of these extrasolar planets, a term usually shortened to “exoplanets,” have been found, including a few potentially Earth- like worlds, along with bizarre objects that bear no resemblance to any of the planets in our solar system. Two of these exoplanet explorers, Michel Mayor and Didier Queloz, were recently awarded half of the Nobel Prize in Physics for the discovery they made in 1995. My colleagues and I are united in our admiration for their pioneering work, and in our pride to be continuing what they began. But there is something peculiar about the Nobel Prize citation. It says: “for the discovery of an exoplanet orbiting a solar-type star.” Shouldn’t it say the first exoplanet? After all, hundreds of astronomers have discovered an exoplanet. I’ve helped find a few. Even high school students and amateur astronomers have discovered them. Did the Nobel Committee make a typographical error? No, they did not, and thereby hangs a tale. Just as it is problematic to decide who discovered America (Christopher Columbus? John Cabot? Leif Erikson? Amerigo Vespucci, whose name is the one that stuck? Those who came on foot from Siberia tens of thousands of years ago?) it is difficult to say who discovered the first exoplanet.
    [Show full text]
  • Arxiv:2010.00015V3 [Hep-Ph] 26 Apr 2021 Galactic Halo Can Scatter with Exoplanets, Lose Energy, and Gles Are the Same Set of Planets, Without DM Heating
    MIT-CTP/5230 SLAC-PUB-17556 Exoplanets as Sub-GeV Dark Matter Detectors Rebecca K. Leane1, 2, ∗ and Juri Smirnov3, 4, y 1Center for Theoretical Physics, Massachusetts Institute of Technology, Cambridge, MA 02139, USA 2SLAC National Accelerator Laboratory, Stanford University, Stanford, CA 94039, USA 3Center for Cosmology and AstroParticle Physics (CCAPP), The Ohio State University, Columbus, OH 43210, USA 4Department of Physics, The Ohio State University, Columbus, OH 43210, USA (Dated: April 27, 2021) We present exoplanets as new targets to discover Dark Matter (DM). Throughout the Milky Way, DM can scatter, become captured, deposit annihilation energy, and increase the heat flow within exoplanets. We estimate upcoming infrared telescope sensitivity to this scenario, finding actionable discovery or exclusion searches. We find that DM with masses above about an MeV can be probed with exoplanets, with DM-proton and DM-electron scattering cross sections down to about 10−37cm2, stronger than existing limits by up to six orders of magnitude. Supporting evidence of a DM origin can be identified through DM-induced exoplanet heating correlated with Galactic position, and hence DM density. This provides new motivation to measure the temperature of the billions of brown dwarfs, rogue planets, and gas giants peppered throughout our Galaxy. Introduction{Are we alone in the Universe? This ques- Exoplanet Temperatures tion has driven wide-reaching interest in discovering a 104 planet like our own. Regardless of whether or not we ever find alien life, the scientific advances from finding DM Heating and understanding other planets will be enormous. From a particle physics perspective, new celestial bodies pro- vide a vast playground to discover new physics.
    [Show full text]
  • Extra-Solar Planets 2
    REVIEW ARTICLE Extra-solar planets M A C Perryman Astrophysics Division, European Space Agency, ESTEC, Noordwijk 2200AG, The Netherlands; and Leiden Observatory, University of Leiden, The Netherlands Abstract. The discovery of the first extra-solar planet surrounding a main-sequence star was announced in 1995, based on very precise radial velocity (Doppler) measurements. A total of 34 such planets were known by the end of March 2000, and their numbers are growing steadily. The newly-discovered systems confirm some of the features predicted by standard theories of star and planet formation, but systems with massive planets having very small orbital radii and large eccentricities are common and were generally unexpected. Other techniques being used to search for planetary signatures include accurate measurement of positional (astrometric) displacements, gravitational microlensing, and pulsar timing, the latter resulting in the detection of the first planetary mass bodies beyond our Solar System in 1992. The transit of a planet across the face of the host star provides significant physical diagnostics, and the first such detection was announced in 1999. Protoplanetary disks, which represent an important evolutionary stage for understanding planet formation, are being imaged from space. In contrast, direct imaging of extra-solar planets represents an enormous challenge. Long-term efforts are directed towards infrared space interferometry, the detection of Earth-mass planets, and measurement of their spectral characteristics. Theoretical atmospheric models provide predictions of planetary temperatures, radii, albedos, chemical condensates, and spectral features as a function of mass, composition and distance from the host star. Efforts to characterise planets occupying the ‘habitable zone’, in which liquid water may be present, and indicators of the arXiv:astro-ph/0005602v1 31 May 2000 presence of life, are advancing quantitatively.
    [Show full text]