Optimal Pacing for Running 400- and 800-M Track Races James Reardon
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Athletics Records
Best Personal Counseling & Guidance about SSB Contact - R S Rathore @ 9001262627 visit us - www.targetssbinterview.com Athletics Records - 1. 100 Meters Usain Bolt, Jamaica, 9.58. Bolt, who was once a 200-meter specialist, broke the 100-meter world mark for the third time during a thrilling showdown with Tyson Gay at the World Outdoor Championships in Berlin on Aug. 16, 2009. The Jamaican pulled ahead of Gay early in the race and never let up, finishing in 9.58 seconds. The victory came exactly one year after Bolt broke the record for the second time, winning the 2008 Olympic gold medal in 9.69. 2. 200 Meters Usain Bolt, Jamaica, 19.19. Bolt broke his own world mark at the 2009 World Outdoor Track & Field Championships, where he finished in 19.19 seconds on Aug. 20. He first broke Michael Johnson's 12-year-old mark during the Olympic final exactly one year earlier, finishing in 19.30 seconds while running into a slight headwind (0.9 kilometers per hour). 3. 400 Meters Michael Johnson, USA, 43.18. Many expected Johnson to eventually break Butch Reynolds' mark of 43.29 seconds, set in 1988, but 1999 seemed an unlikely year for the record to fall. Johnson suffered from leg injuries that season, missed the U.S. Championships and ran only four 400-meter races before the World Championships (where he gained an automatic entry as the defending champ). By the day of the World final, however, it was apparent that Johnson was in top form and that Reynolds' record was in jeopardy. -

Braves Middle Distance and Long Sprint Philosophy
Distance Training for Track By Rob Marriott Personal Introduction • 1987 Osawatomie HS grad with PRs of 4:35, 2:02(relay split), :52.8(relay split) and 10:29(CC). • 1992 Ottawa University grad with PRs of 4:01 (1500), 1:56, 9:48(Indoor 2 mile), 15:48(Road), 26:50 (8K). • Avid road racer from 1993-2009. Still somewhat active. Boston Marathon qualifier 2008, 2009 and 2010. Coaching Experience • Paola Panthers 1992-2007 • Bonner Springs Braves 2007-2015 • Leavenworth Pioneers 2015-2016 • 24 years of both CC and Track Coaching Guidelines 1. Give back. 2. Commit to improving every year. 3. Leave your mind open to new things. 4. Make kids a priority. 5. Become a student of the sport. 6. Get parents involved. 7. Coach with integrity. Be a positive example. Advice for New Coaches • Find a mentor. Not just someone else on your coaching staff but someone from another school. Veteran HS Track and CC coaches are more than happy to share what they do. • Steal other coaches methods. Everything I do has been stolen from someone else. I truly have nothing original to offer. • Always continue to listen to other coaches ideas. Keep the ones you like and add them to your own bag of tricks. • Go to clinics as often as possible. I go to two or three per year. In 24 years, I’ve never gone to a clinic and not added something to my repertoire. • Get Jack Daniels and Joe Vigil’s books. Types of Distance Runners • 200M-800M type: These will spend 1-2 days each week with the sprint crew but most days with me. -
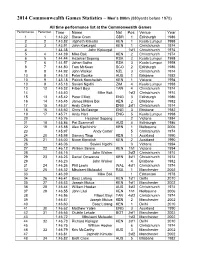
2014 Commonwealth Games Statistics – Men's 800M
2014 Commonwealth Games Statistics – Men’s 800m (880yards before 1970) All time performance list at the Commonwealth Games Performance Performer Time Name Nat Pos Venue Year 1 1 1:43.22 Steve Cram GBR 1 Edinburgh 1986 2 2 1:43.82 Japheth Kimutai KEN 1 Kuala Lumpur 1998 3 3 1:43.91 John Kipkurgat KEN 1 Christchurch 1974 4 1:44.38 John Kipkurgat 1sf1 Christchurch 1974 5 4 1:44.39 Mike Boit KEN 2 Christchurch 1974 6 5 1:44.44 Hezekiel Sepeng RSA 2 Kuala Lumpur 1998 7 6 1:44.57 Johan Botha RSA 3 Kuala Lumpur 1998 8 7 1:44.80 Tom McKean SCO 2 Edinburgh 1986 9 8 1:44.92 John Walker NZL 3 Christchurch 1974 10 9 1:45.18 Peter Bourke AUS 1 Brisbane 1982 10 9 1:45.18 Patrick Konchellah KEN 1 Victoria 1994 10 9 1:45.18 Savieri Ngidhi ZIM 4 Kuala Lumpur 1998 13 12 1:45.32 Filbert Bayi TAN 4 Christchurch 1974 14 1:45.40 Mike Boit 1sf2 Christchurch 1974 15 13 1:45.42 Peter Elliott ENG 3 Edinburgh 1986 16 14 1:45.45 James Maina Boi KEN 2 Brisbane 1982 17 15 1:45.57 Andy Carter ENG 2sf1 Christchurch 1974 18 16 1:45.60 Chris McGeorge ENG 3 Brisbane 1982 19 17 1:45.71 Andy Hart ENG 5 Kuala Lumpur 1998 20 1:45.76 Hezekiel Sepeng 2 Victoria 1994 21 18 1:45.86 Pat Scammell AUS 4 Edinburgh 1986 22 19 1:45.88 Alex Kipchirchir KEN 1 Melbourne 2006 23 1:45.97 Andy Carter 5 Christchurch 1974 24 20 1:45.98 Sammy Tirop KEN 1 Auckland 1990 25 21 1:46.00 Nixon Kiprotich KEN 2 Auckland 1990 26 1:46.06 Savieri Ngidhi 3 Victoria 1994 27 22 1:46.12 William Serem KEN 1h1 Victoria 1994 28 1:46.15 John Walker 2sf2 Christchurch 1974 29 23 1:46.23 Daniel Omwanza KEN 3sf1 Christchurch -

Success on the World Stage Athletics Australia Annual Report 2010–2011 Contents
Success on the World Stage Athletics Australia Annual Report Success on the World Stage Athletics Australia 2010–2011 2010–2011 Annual Report Contents From the President 4 From the Chief Executive Officers 6 From The Australian Sports Commission 8 High Performance 10 High Performance Pathways Program 14 Competitions 16 Marketing and Communications 18 Coach Development 22 Running Australia 26 Life Governors/Members and Merit Award Holders 27 Australian Honours List 35 Vale 36 Registration & Participation 38 Australian Records 40 Australian Medalists 41 Athletics ACT 44 Athletics New South Wales 46 Athletics Northern Territory 48 Queensland Athletics 50 Athletics South Australia 52 Athletics Tasmania 54 Athletics Victoria 56 Athletics Western Australia 58 Australian Olympic Committee 60 Australian Paralympic Committee 62 Financial Report 64 Chief Financial Officer’s Report 66 Directors’ Report 72 Auditors Independence Declaration 76 Income Statement 77 Statement of Comprehensive Income 78 Statement of Financial Position 79 Statement of Changes in Equity 80 Cash Flow Statement 81 Notes to the Financial Statements 82 Directors’ Declaration 103 Independent Audit Report 104 Trust Funds 107 Staff 108 Commissions and Committees 109 2 ATHLETICS AuSTRALIA ANNuAL Report 2010 –2011 | SuCCESS ON THE WORLD STAGE 3 From the President Chief Executive Dallas O’Brien now has his field in our region. The leadership and skillful feet well and truly beneath the desk and I management provided by Geoff and Yvonne congratulate him on his continued effort to along with the Oceania Council ensures a vast learn the many and numerous functions of his array of Athletics programs can be enjoyed by position with skill, patience and competence. -

Optimal Pacing for Running 400 M and 800 M Track Races
Optimal Pacing for Running 400 m and 800 m Track Races James Reardon University of Wisconsin–Madison, Department of Physics, Madison, WI 53706∗ (Dated: April 3, 2012) Physicists seeking to understand complex biological systems often find it rewarding to create simple “toy models” that reproduce system behavior. Here a toy model is used to understand a puzzling phenomenon from the sport of track and field. Races are almost always won, and records set, in 400 m and 800 m running events by people who run the first half of the race faster than the second half, which is not true of shorter races, nor of longer. There is general agreement that performance in the 400 m and 800 m is limited somehow by the amount of anaerobic metabolism that can be tolerated in the working muscles in the legs. A toy model of anaerobic metabolism is presented, from which an optimal pacing strategy is analytically calculated via the Euler-Lagrange equation. This optimal strategy is then modified to account for the fact that the runner starts the race from rest; this modification is shown to result in the best possible outcome by use of an elementary variational technique that supplements what is found in undergraduate textbooks. The toy model reproduces the pacing strategies of elite 400 m and 800 m runners better than existing models do. The toy model also gives some insight into training strategies that improve performance. arXiv:1204.0313v1 [physics.pop-ph] 2 Apr 2012 2 I. INTRODUCTION The sport of athletics, called “track and field” in the USA, includes running competitions at distances ranging from 60 m to 10000 m. -

Flash Results, Inc. - Contractor License 4/18/2013 - 4:13 PM 55Th ANNUAL MT
Flash Results, Inc. - Contractor License 4/18/2013 - 4:13 PM 55th ANNUAL MT. SAC RELAYS "Where the world's best athletes compete" Hilmer Lodge Stadium, Walnut, California - 4/18/2013 to 4/20/2 Event 243 Women 4x100 Meter Shuttle Hurdle Open U/O =============================================================== American Rec: @ 52.38 2012 , Star Athletics Team Finals =============================================================== Finals 1 Academy of Art 'A' 54.04 1) Vashti Thomas 2) Briana Stewart 3) Julian Purvis 4) Dinesha Bean 2 Kansas State 'A' 56.89 1) Richelle Farley 2) Erica Twiss 3) Jordan Matthews 4) Sarah Kolmer 3 Wichita State 'A' 57.31 1) Natalie Morerod 2) Shanice Andrews 3) Taylor Thomas 4) Nikki Larch-Miller Event 143 Men 4x110 Meter Shuttle Hurdle Open U/O =============================================================== Team Finals =============================================================== Finals 1 Sacramento St. 'A' 59.38 1) Casey Wheeler 2) Anthony Williams 3) Tyler Creswell 4) Paul Lyons Event 236 Women 4x100 Meter Relay Open U/O ================================================================ Team Finals ================================================================ Section 1 1 Nevada 'A' 45.10 1) Samantha Calhoun 2) Angelica Earls 3) Tanisha Hawkins 4) Kashae Knox 2 Cal State Northridge 'A' 45.22 1) Leshel Vines 2) Hafsatu Kamara 3) Lexis Lambert 4) Marie Veale 3 Washington St. 'A' 45.37 1) Cindy Robinson 2) Dominique Keel 3) Christiana Ekelem 4) Shawna Fermin 4 Boise State 'A' 45.67 1) Heather Pilcher 2) Taryn Campos 3) Mackenzie Flannigan 4) Destiny Gammage 5 Cal St. Fullerton 'A' 46.42 1) Ashley Sims 2) Katie Wilson 3) Morgan Thompson 4) Alexandria Stewart 6 West Texas A&M 'A' 46.53 1) Carnisha Simpson 2) Bri Leeper 3) Sarah Snider 4) Paula Bowens 7 Sacramento St. -

All Time Men's World Ranking Leader
All Time Men’s World Ranking Leader EVER WONDER WHO the overall best performers have been in our authoritative World Rankings for men, which began with the 1947 season? Stats Editor Jim Rorick has pulled together all kinds of numbers for you, scoring the annual Top 10s on a 10-9-8-7-6-5-4-3-2-1 basis. First, in a by-event compilation, you’ll find the leaders in the categories of Most Points, Most Rankings, Most No. 1s and The Top U.S. Scorers (in the World Rankings, not the U.S. Rankings). Following that are the stats on an all-events basis. All the data is as of the end of the 2019 season, including a significant number of recastings based on the many retests that were carried out on old samples and resulted in doping positives. (as of April 13, 2020) Event-By-Event Tabulations 100 METERS Most Points 1. Carl Lewis 123; 2. Asafa Powell 98; 3. Linford Christie 93; 4. Justin Gatlin 90; 5. Usain Bolt 85; 6. Maurice Greene 69; 7. Dennis Mitchell 65; 8. Frank Fredericks 61; 9. Calvin Smith 58; 10. Valeriy Borzov 57. Most Rankings 1. Lewis 16; 2. Powell 13; 3. Christie 12; 4. tie, Fredericks, Gatlin, Mitchell & Smith 10. Consecutive—Lewis 15. Most No. 1s 1. Lewis 6; 2. tie, Bolt & Greene 5; 4. Gatlin 4; 5. tie, Bob Hayes & Bobby Morrow 3. Consecutive—Greene & Lewis 5. 200 METERS Most Points 1. Frank Fredericks 105; 2. Usain Bolt 103; 3. Pietro Mennea 87; 4. Michael Johnson 81; 5. -

September/October 2010 Bronx N
SEPTEMBER/OCTOBER 2010 BRONX N. Y. VOLUME 43 ISSUE #5 Van Cortlandt Track Club newsletter My Kenyan Adventure by Kyle Ha! This summer presented me with one of those unique moments in life when I knew I had to strike while the iron was hot. Everything came together running-wise, financially, & in terms of my summer break from teaching. I was then off to Africa. My flights all went well. Emirates is an incredible airline and I ate very well onboard (i.e. grilled tofu with vegetables, fruit salads, Indian rice with beans, etc.) There were literally hundreds of movies and tv shows to watch and everyone had his/her own individual tv screen and advanced remote. 'Stars' lit up the cabin ceiling at night. The flight was 11 hours 41 minutes from JFK to Dubai, United Arab Emirates. I landed in the Middle East for the first time ever and was immediately struck by the opulence of Dubai. Giant sparkling columns lined the high ceilinged airport. Triple story cascading Kyle with Daniel Rono by the pool at th" waterfalls fell near giant elevators. All local Muslim women I saw High Altitude Training Centr" had their heads covered and men wore flowing white robes with long white head scarves (sorry, I don't know the proper terms for those). The world's only 7 star hotel, Al Burj Dubai, sat nearby--on its own private island. The airport's Burger King carried the 'Bean Patty--Veg' sandwich. Of course, I left the airport and explored a bit outside but then had to report back to Emirates fairly quickly for my connecting flight. -

Men's 200M Final 23.08.2020
Men's 200m Final 23.08.2020 Start list 200m Time: 17:10 Records Lane Athlete Nat NR PB SB 1 Richard KILTY GBR 19.94 20.34 WR 19.19 Usain BOLT JAM Olympiastadion, Berlin 20.08.09 2 Mario BURKE BAR 19.97 20.08 20.78 AR 19.72 Pietro MENNEA ITA Ciudad de México 12.09.79 3 Felix SVENSSON SWE 20.30 20.73 20.80 NR 20.30 Johan WISSMAN SWE Stuttgart 23.09.07 WJR 19.93 Usain BOLT JAM Hamilton 11.04.04 4 Jan VELEBA CZE 20.46 20.64 20.64 MR 19.77 Michael JOHNSON USA 08.07.96 5 Silvan WICKI SUI 19.98 20.45 20.45 DLR 19.26 Yohan BLAKE JAM Boudewijnstadion, Bruxelles 16.09.11 6 Adam GEMILI GBR 19.94 19.97 20.56 SB 19.76 Noah LYLES USA Stade Louis II, Monaco 14.08.20 7 Bruno HORTELANO-ROIG ESP 20.04 20.04 8 Elijah HALL USA 19.32 20.11 20.69 2020 World Outdoor list 19.76 +0.7 Noah LYLES USA Stade Louis II, Monaco (MON) 14.08.20 19.80 +1.0 Kenneth BEDNAREK USA Montverde, FL (USA) 10.08.20 Medal Winners Stockholm previous 19.96 +1.0 Steven GARDINER BAH Clermont, FL (USA) 25.07.20 20.22 +0.8 Divine ODUDURU NGR Clermont, FL (USA) 25.07.20 2019 - IAAF World Ch. in Athletics Winners 20.23 +0.1 Clarence MUNYAI RSA Pretoria (RSA) 13.03.20 1. Noah LYLES (USA) 19.83 19 Aaron BROWN (CAN) 20.06 20.24 +0.8 André DE GRASSE CAN Clermont, FL (USA) 25.07.20 2. -

Men's 200M Diamond Discipline 03.05.2019
Men's 200m Diamond Discipline 03.05.2019 Start list 200m Time: 19:56 Records Lane Athlete Nat NR PB SB 1 Owaab BARROW QAT 19.97 21.87 WR 19.19 Usain BOLT JAM Berlin 20.08.09 2 Leon REID IRL 20.27 21.04 AR 19.97 Femi OGUNODE QAT Bruxelles 11.09.15 3 Jaber Hilal AL MAMARI QAT 19.97 21.74 21.90 NR 19.97 Femi OGUNODE QAT Bruxelles 11.09.15 WJR 19.93 Usain BOLT JAM Hamilton 11.04.04 4 Alex QUIÑÓNEZ ECU 19.93 19.93 20.28 MR 19.83 Noah LYLES USA 04.05.18 5 Aaron BROWN CAN 19.80 19.98 DLR 19.26 Yohan BLAKE JAM Bruxelles 16.09.11 6 Ramil GULIYEV TUR 19.76 19.76 SB 19.76 Divine ODUDURU NGR Waco, TX 20.04.19 7 Alonso EDWARD PAN 19.81 19.81 8 Nethaneel MITCHELL-BLAKE GBR 19.94 19.95 9 Jereem RICHARDS TTO 19.77 19.97 20.45 2019 World Outdoor list 19.76 +0.8 Divine ODUDURU NGR Waco, TX 20.04.19 20.04 +1.4 Steven GARDINER BAH Coral Gables, FL 13.04.19 20.08 +0.9 Bernardo BALOYES COL Bragança Paulista 28.04.19 Medal Winners Doha previous Winners 20.16 +1.0 Miguel FRANCIS GBR St. George's 13.04.19 20.20 +1.0 Andre DE GRASSE CAN St. George's 13.04.19 2019 - Doha Asian Ch. 18 Noah LYLES (USA) 19.83 20.20 +2.0 Nick GRAY USA Columbia, SC 13.04.19 16 Ameer WEBB (USA) 19.85 20.21 +0.9 Gabriel CONSTANTINO BRA Bragança Paulista 28.04.19 1. -

Doha 2018: Compact Athletes' Bios (PDF)
Men's 200m Diamond Discipline 04.05.2018 Start list 200m Time: 20:36 Records Lane Athlete Nat NR PB SB 1 Rasheed DWYER JAM 19.19 19.80 20.34 WR 19.19 Usain BOLT JAM Berlin 20.08.09 2 Omar MCLEOD JAM 19.19 20.49 20.49 AR 19.97 Femi OGUNODE QAT Bruxelles 11.09.15 NR 19.97 Femi OGUNODE QAT Bruxelles 11.09.15 3 Nethaneel MITCHELL-BLAKE GBR 19.94 19.95 WJR 19.93 Usain BOLT JAM Hamilton 11.04.04 4 Andre DE GRASSE CAN 19.80 19.80 MR 19.85 Ameer WEBB USA 06.05.16 5 Ramil GULIYEV TUR 19.88 19.88 DLR 19.26 Yohan BLAKE JAM Bruxelles 16.09.11 6 Jereem RICHARDS TTO 19.77 19.97 20.12 SB 19.69 Clarence MUNYAI RSA Pretoria 16.03.18 7 Noah LYLES USA 19.32 19.90 8 Aaron BROWN CAN 19.80 20.00 20.18 2018 World Outdoor list 19.69 -0.5 Clarence MUNYAI RSA Pretoria 16.03.18 19.75 +0.3 Steven GARDINER BAH Coral Gables, FL 07.04.18 Medal Winners Doha previous Winners 20.00 +1.9 Ncincihli TITI RSA Columbia 21.04.18 20.01 +1.9 Luxolo ADAMS RSA Paarl 22.03.18 16 Ameer WEBB (USA) 19.85 2017 - London IAAF World Ch. in 20.06 -1.4 Michael NORMAN USA Tempe, AZ 07.04.18 14 Nickel ASHMEADE (JAM) 20.13 Athletics 20.07 +1.9 Anaso JOBODWANA RSA Paarl 22.03.18 12 Walter DIX (USA) 20.02 20.10 +1.0 Isaac MAKWALA BOT Gaborone 29.04.18 1. -

Men's 200M Diamond Discipline 26.08.2021
Men's 200m Diamond Discipline 26.08.2021 Start list 200m Time: 21:35 Records Lane Athlete Nat NR PB SB 1 Eseosa Fostine DESALU ITA 19.72 20.13 20.29 WR 19.19 Usain BOLT JAM Olympiastadion, Berlin 20.08.09 2 Isiah YOUNG USA 19.32 19.86 19.99 AR 19.72 Pietro MENNEA ITA Ciudad de México 12.09.79 3 Yancarlos MARTÍNEZ DOM 20.17 20.17 20.17 NR 19.98 Alex WILSON SUI La Chaux-de-Fonds 30.06.19 WJR* 19.84 Erriyon KNIGHTON USA Hayward Field, Eugene, OR 27.06.21 4Aaron BROWN CAN19.6219.9519.99WJR 19.88 Erriyon KNIGHTON USA Hayward Field, Eugene, OR 26.06.21 5Fred KERLEY USA19.3219.9019.90MR 19.50 Noah LYLES USA 05.07.19 6Kenneth BEDNAREKUSA19.3219.6819.68DLR 19.26 Yohan BLAKE JAM Boudewijnstadion, Bruxelles 16.09.11 7 Steven GARDINER BAH 19.75 19.75 20.24 SB 19.52 Noah LYLES USA Hayward Field, Eugene, OR 21.08.21 8William REAIS SUI19.9820.2420.26 2021 World Outdoor list 19.52 +1.5 Noah LYLES USA Eugene, OR (USA) 21.08.21 Medal Winners Road To The Final 19.62 -0.5 André DE GRASSE CAN Olympic Stadium, Tokyo (JPN) 04.08.21 1Aaron BROWN (CAN) 25 19.68 -0.5 Kenneth BEDNAREK USA Olympic Stadium, Tokyo (JPN) 04.08.21 2021 - The XXXII Olympic Games 2Kenneth BEDNAREK (USA) 23 19.81 +0.8 Terrance LAIRD USA Austin, TX (USA) 27.03.21 1. André DE GRASSE (CAN) 19.62 3André DE GRASSE (CAN) 21 19.84 +0.3 Erriyon KNIGHTON USA Eugene, OR (USA) 27.06.21 2.