Optimal Pacing for Running 400 M and 800 M Track Races
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

© 21St Century Math Projects
© 21st Century Math Projects Project Title: Mile Run Standard Focus: Data Analysis, Patterns, Algebra & Time Range: 3-4 Days Functions Supplies: TI Graphing Technology Topics of Focus: - Scatterplots - Creating and Applying Regression Functions - Interpolation & Extrapolation of Data Benchmarks: 4. For a function that models a relationship between two quantities, interpret key Interpreting F-IF features of graphs and tables in terms of the quantities, and sketch graphs showing key Functions features given a verbal description of the relationship. 6. Calculate and interpret the average rate of change of a function (presented Interpreting F-IF symbolically or as a table) over a specified interval. Estimate the rate of change from a Functions graph.★ Building Functions F-BF 1. Write a function that describes a relationship between two quantities.★ Interpreting 6a. Fit a function to the data; use functions fitted to data to solve problems in the Categorical and S-ID context of the data. Use given functions or choose a function suggested by the context. Quantitative Data Emphasize linear and exponential models. Interpreting Categorical and S-ID 6c. Fit a linear function for a scatter plot that suggests a linear association. Quantitative Data Procedures: A.) Students will use Graphing Calculator Technology to make scatterplots using data from the “Mile Run Chart”. (Graphing Calculator Instructions insert included) B.) Students will complete the three parts of the Mile Run Project. © 21st Century Math Projects The Mile Run In 1593, the English Parliament declared that 5,280 feet would equal 1 mile. Ever since, a mile run has become a staple fitness test everywhere -- from militaries to the high school gyms. -

Athletics Records
Best Personal Counseling & Guidance about SSB Contact - R S Rathore @ 9001262627 visit us - www.targetssbinterview.com Athletics Records - 1. 100 Meters Usain Bolt, Jamaica, 9.58. Bolt, who was once a 200-meter specialist, broke the 100-meter world mark for the third time during a thrilling showdown with Tyson Gay at the World Outdoor Championships in Berlin on Aug. 16, 2009. The Jamaican pulled ahead of Gay early in the race and never let up, finishing in 9.58 seconds. The victory came exactly one year after Bolt broke the record for the second time, winning the 2008 Olympic gold medal in 9.69. 2. 200 Meters Usain Bolt, Jamaica, 19.19. Bolt broke his own world mark at the 2009 World Outdoor Track & Field Championships, where he finished in 19.19 seconds on Aug. 20. He first broke Michael Johnson's 12-year-old mark during the Olympic final exactly one year earlier, finishing in 19.30 seconds while running into a slight headwind (0.9 kilometers per hour). 3. 400 Meters Michael Johnson, USA, 43.18. Many expected Johnson to eventually break Butch Reynolds' mark of 43.29 seconds, set in 1988, but 1999 seemed an unlikely year for the record to fall. Johnson suffered from leg injuries that season, missed the U.S. Championships and ran only four 400-meter races before the World Championships (where he gained an automatic entry as the defending champ). By the day of the World final, however, it was apparent that Johnson was in top form and that Reynolds' record was in jeopardy. -

Cor-07-00858
A Reporter’s Guide to Sports and Olympics Reporting Contents Preface 3 Reporting the Olympics 26 Introduction 5 Your role 26 Writing about sport 6 Preparations 26 Accuracy 8 The Games 29 The intro 8 Surviving the mixed zone 30 The match/race report 9 Olympic News Service 30 Quotes and interviews 11 Stars, personalities 32 Some tips on interviewing 15 Reporting the highlights 35 Adding human interest 16 Drugs at the Olympics 35 Features 16 Breaking news stories 36 There are many ways of leading a feature 18 Feature, off-beat, human interest, humorous stories 38 Sponsorship 23 Unusual sports and events 40 Drugs 23 Winter Olympics 40 Some useful websites 24 Tips for the Olympics reporter 42 General sites 24 Photo credits 43 © Reuters 2008. All rights reserved. Reuters and the sphere logo are the trademarks or registered trademarks of the Reuters group of companies around the world. COR-07-00964 Preface During the ancient Olympics, there was a moratorium on wars to allow people across the region to attend the Games. While it is probably too much to expect this to happen today, the ability of sport in general and the Olympic Games in particular to bring countries peacefully together is beyond question. After Cold War boycotts led by Soviet and U.S. teams during the 1980s, the Games have been largely free of political protests since 1988. And in Beijing in 2008, North and South Korea are due to field a joint team for the first time since the peninsula was divided 60 years ago. For journalists covering the Olympics, the task of following their home athletes through 302 different events in 28 sports is challenging enough. -

Braves Middle Distance and Long Sprint Philosophy
Distance Training for Track By Rob Marriott Personal Introduction • 1987 Osawatomie HS grad with PRs of 4:35, 2:02(relay split), :52.8(relay split) and 10:29(CC). • 1992 Ottawa University grad with PRs of 4:01 (1500), 1:56, 9:48(Indoor 2 mile), 15:48(Road), 26:50 (8K). • Avid road racer from 1993-2009. Still somewhat active. Boston Marathon qualifier 2008, 2009 and 2010. Coaching Experience • Paola Panthers 1992-2007 • Bonner Springs Braves 2007-2015 • Leavenworth Pioneers 2015-2016 • 24 years of both CC and Track Coaching Guidelines 1. Give back. 2. Commit to improving every year. 3. Leave your mind open to new things. 4. Make kids a priority. 5. Become a student of the sport. 6. Get parents involved. 7. Coach with integrity. Be a positive example. Advice for New Coaches • Find a mentor. Not just someone else on your coaching staff but someone from another school. Veteran HS Track and CC coaches are more than happy to share what they do. • Steal other coaches methods. Everything I do has been stolen from someone else. I truly have nothing original to offer. • Always continue to listen to other coaches ideas. Keep the ones you like and add them to your own bag of tricks. • Go to clinics as often as possible. I go to two or three per year. In 24 years, I’ve never gone to a clinic and not added something to my repertoire. • Get Jack Daniels and Joe Vigil’s books. Types of Distance Runners • 200M-800M type: These will spend 1-2 days each week with the sprint crew but most days with me. -
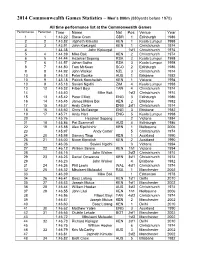
2014 Commonwealth Games Statistics – Men's 800M
2014 Commonwealth Games Statistics – Men’s 800m (880yards before 1970) All time performance list at the Commonwealth Games Performance Performer Time Name Nat Pos Venue Year 1 1 1:43.22 Steve Cram GBR 1 Edinburgh 1986 2 2 1:43.82 Japheth Kimutai KEN 1 Kuala Lumpur 1998 3 3 1:43.91 John Kipkurgat KEN 1 Christchurch 1974 4 1:44.38 John Kipkurgat 1sf1 Christchurch 1974 5 4 1:44.39 Mike Boit KEN 2 Christchurch 1974 6 5 1:44.44 Hezekiel Sepeng RSA 2 Kuala Lumpur 1998 7 6 1:44.57 Johan Botha RSA 3 Kuala Lumpur 1998 8 7 1:44.80 Tom McKean SCO 2 Edinburgh 1986 9 8 1:44.92 John Walker NZL 3 Christchurch 1974 10 9 1:45.18 Peter Bourke AUS 1 Brisbane 1982 10 9 1:45.18 Patrick Konchellah KEN 1 Victoria 1994 10 9 1:45.18 Savieri Ngidhi ZIM 4 Kuala Lumpur 1998 13 12 1:45.32 Filbert Bayi TAN 4 Christchurch 1974 14 1:45.40 Mike Boit 1sf2 Christchurch 1974 15 13 1:45.42 Peter Elliott ENG 3 Edinburgh 1986 16 14 1:45.45 James Maina Boi KEN 2 Brisbane 1982 17 15 1:45.57 Andy Carter ENG 2sf1 Christchurch 1974 18 16 1:45.60 Chris McGeorge ENG 3 Brisbane 1982 19 17 1:45.71 Andy Hart ENG 5 Kuala Lumpur 1998 20 1:45.76 Hezekiel Sepeng 2 Victoria 1994 21 18 1:45.86 Pat Scammell AUS 4 Edinburgh 1986 22 19 1:45.88 Alex Kipchirchir KEN 1 Melbourne 2006 23 1:45.97 Andy Carter 5 Christchurch 1974 24 20 1:45.98 Sammy Tirop KEN 1 Auckland 1990 25 21 1:46.00 Nixon Kiprotich KEN 2 Auckland 1990 26 1:46.06 Savieri Ngidhi 3 Victoria 1994 27 22 1:46.12 William Serem KEN 1h1 Victoria 1994 28 1:46.15 John Walker 2sf2 Christchurch 1974 29 23 1:46.23 Daniel Omwanza KEN 3sf1 Christchurch -

Success on the World Stage Athletics Australia Annual Report 2010–2011 Contents
Success on the World Stage Athletics Australia Annual Report Success on the World Stage Athletics Australia 2010–2011 2010–2011 Annual Report Contents From the President 4 From the Chief Executive Officers 6 From The Australian Sports Commission 8 High Performance 10 High Performance Pathways Program 14 Competitions 16 Marketing and Communications 18 Coach Development 22 Running Australia 26 Life Governors/Members and Merit Award Holders 27 Australian Honours List 35 Vale 36 Registration & Participation 38 Australian Records 40 Australian Medalists 41 Athletics ACT 44 Athletics New South Wales 46 Athletics Northern Territory 48 Queensland Athletics 50 Athletics South Australia 52 Athletics Tasmania 54 Athletics Victoria 56 Athletics Western Australia 58 Australian Olympic Committee 60 Australian Paralympic Committee 62 Financial Report 64 Chief Financial Officer’s Report 66 Directors’ Report 72 Auditors Independence Declaration 76 Income Statement 77 Statement of Comprehensive Income 78 Statement of Financial Position 79 Statement of Changes in Equity 80 Cash Flow Statement 81 Notes to the Financial Statements 82 Directors’ Declaration 103 Independent Audit Report 104 Trust Funds 107 Staff 108 Commissions and Committees 109 2 ATHLETICS AuSTRALIA ANNuAL Report 2010 –2011 | SuCCESS ON THE WORLD STAGE 3 From the President Chief Executive Dallas O’Brien now has his field in our region. The leadership and skillful feet well and truly beneath the desk and I management provided by Geoff and Yvonne congratulate him on his continued effort to along with the Oceania Council ensures a vast learn the many and numerous functions of his array of Athletics programs can be enjoyed by position with skill, patience and competence. -

RESULTS 1500 Metres Men - Final
Doha (QAT) 27 September - 6 October 2019 RESULTS 1500 Metres Men - Final RECORDS RESULT NAME COUNTRY AGE VENUE DATE World Record WR 3:26.00 Hicham EL GUERROUJ MAR 24 Roma (Stadio Olimpico) 14 Jul 1998 Championships Record CR 3:27.65 Hicham EL GUERROUJ MAR 25 Sevilla (La Cartuja) 24 Aug 1999 World Leading WL 3:28.77 Timothy CHERUIYOT KEN 24 Lausanne (Pontaise) 5 Jul 2019 Area Record AR National Record NR Personal Best PB Season Best SB 6 October 2019 19:41 START TIME 24° C 64 % TEMPERATURE HUMIDITY PLACE NAME COUNTRY DATE of BIRTH ORDER RESULT 1 Timothy CHERUIYOT KEN 20 Nov 95 2 3:29.26 2 Taoufik MAKHLOUFI ALG 29 Apr 88 4 3:31.38 SB 3 Marcin LEWANDOWSKI POL 13 Jun 87 9 3:31.46 NR 4 Jakob INGEBRIGTSEN NOR 19 Sep 00 6 3:31.70 5 Jake WIGHTMAN GBR 11 Jul 94 12 3:31.87 PB 6 Josh KERR GBR 8 Oct 97 1 3:32.52 PB 7 Ronald KWEMOI KEN 19 Sep 95 7 3:32.72 SB 8 Matthew CENTROWITZ USA 18 Oct 89 3 3:32.81 SB 9 Kalle BERGLUND SWE 11 Mar 96 11 3:33.70 NR 10 Craig ENGELS USA 1 May 94 10 3:34.24 11 Neil GOURLEY GBR 7 Feb 95 5 3:37.30 12 Youssouf HISS BACHIR DJI 1 Jan 87 8 3:37.96 INTERMEDIATE TIMES 100 m13.46 Timothy CHERUIYOT 200 m27.09 Timothy CHERUIYOT 300 m41.06 Timothy CHERUIYOT 400 m55.01 Timothy CHERUIYOT 500 m1:08.91 Timothy CHERUIYOT 600 m1:22.88 Timothy CHERUIYOT 700 m1:40.44 Kalle BERGLUND 800 m1:51.74 Timothy CHERUIYOT 900 m2:06.19 Timothy CHERUIYOT 1000 m2:20.49 Timothy CHERUIYOT 1100 m2:34.54 Timothy CHERUIYOT 1200 m2:48.22 Timothy CHERUIYOT 1300 m3:01.73 Timothy CHERUIYOT 1400 m3:15.37 Timothy CHERUIYOT ALL-TIME TOP LIST SEASON TOP LIST RESULT -

Flash Results, Inc. - Contractor License 4/18/2013 - 4:13 PM 55Th ANNUAL MT
Flash Results, Inc. - Contractor License 4/18/2013 - 4:13 PM 55th ANNUAL MT. SAC RELAYS "Where the world's best athletes compete" Hilmer Lodge Stadium, Walnut, California - 4/18/2013 to 4/20/2 Event 243 Women 4x100 Meter Shuttle Hurdle Open U/O =============================================================== American Rec: @ 52.38 2012 , Star Athletics Team Finals =============================================================== Finals 1 Academy of Art 'A' 54.04 1) Vashti Thomas 2) Briana Stewart 3) Julian Purvis 4) Dinesha Bean 2 Kansas State 'A' 56.89 1) Richelle Farley 2) Erica Twiss 3) Jordan Matthews 4) Sarah Kolmer 3 Wichita State 'A' 57.31 1) Natalie Morerod 2) Shanice Andrews 3) Taylor Thomas 4) Nikki Larch-Miller Event 143 Men 4x110 Meter Shuttle Hurdle Open U/O =============================================================== Team Finals =============================================================== Finals 1 Sacramento St. 'A' 59.38 1) Casey Wheeler 2) Anthony Williams 3) Tyler Creswell 4) Paul Lyons Event 236 Women 4x100 Meter Relay Open U/O ================================================================ Team Finals ================================================================ Section 1 1 Nevada 'A' 45.10 1) Samantha Calhoun 2) Angelica Earls 3) Tanisha Hawkins 4) Kashae Knox 2 Cal State Northridge 'A' 45.22 1) Leshel Vines 2) Hafsatu Kamara 3) Lexis Lambert 4) Marie Veale 3 Washington St. 'A' 45.37 1) Cindy Robinson 2) Dominique Keel 3) Christiana Ekelem 4) Shawna Fermin 4 Boise State 'A' 45.67 1) Heather Pilcher 2) Taryn Campos 3) Mackenzie Flannigan 4) Destiny Gammage 5 Cal St. Fullerton 'A' 46.42 1) Ashley Sims 2) Katie Wilson 3) Morgan Thompson 4) Alexandria Stewart 6 West Texas A&M 'A' 46.53 1) Carnisha Simpson 2) Bri Leeper 3) Sarah Snider 4) Paula Bowens 7 Sacramento St. -

Our Part in Four-Minute Mile History
Our part in four-minute mile history Bruce McAvaney addressed a dinner in Melbourne recently, to commemorate Australian John Landy's first sub-four-minute mile and world record, run 50 years ago, six weeks after Roger Bannister first went under four. This is the transcript of his speech. "Here is the result of event No.9, the one mile: No. 41, R G Bannister, of the Amateur Athletic Association and formerly of Exeter and Merton Colleges, with a time that is a new meeting and track record, and which, subject to ratification, with be a new English native, British National, British all-comers, European, British Empire and World Record. The time is 3…." That's arguably the most famous cue, let alone understated announcement in athletics history…3 Minutes, 59.4 seconds! He was a formidable character, the announcer. Norris McWhirter died earlier this year, unfortunately just before the 50th anniversary of the first sub-four minute mile. McWhirter apparently had rehearsed assiduously the night before, in his bath, and it was through him that the BBC, the newsreel camera and most of the print media were present that day. McWhirter, and his twin Ross, who was gunned down in 1975 by the IRA, were joint founders and editors of the Guinness Book of Records. McWhirter had a sense of humour. Here in Melbourne at the 1956 Olympics, he told the story of a middle-aged Australian woman who, observing distressing scenes at the finish of the marathon exclaimed, "Cripes, how many qualify for the final?"… Back to Bannister, and the race: is it the sport's finest achievement? How does the 3.59.4 stack up with other athletic landmarks? Classics such as our own Ron Clarke's 27:39.4 in Oslo in 1965, a 35 second improvement on the previous mark. -

2011 Ucla Men's Track & Field
2011 MEN’S TRACK & FIELD SCHEDULE IINDOORNDOOR SSEASONEASON Date Meet Location January 28-29 at UW Invitational Seattle, WA February 4-5 at New Balance Collegiate Invitational New York, NY at New Mexico Classic Albuquerque, NM February 11-12 at Husky Classic Seattle, WA February 25-26 at MPSF Indoor Championships Seattle, WA March 5 at UW Final Qualifi er Seattle, WA March 11-12 at NCAA Indoor Championships College Station, TX OOUTDOORUTDOOR SSEASONEASON Date Meet Location March 11-12 at Northridge Invitational Northridge, CA March 18-19 at Aztec Invitational San Diego, CA March 25 vs. Texas & Arkansas Austin, TX April 2 vs. Tennessee ** Drake Stadium April 7-9 Rafer Johnson/Jackie Joyner Kersee Invitational ** Drake Stadium April 14 at Mt. SAC Relays Walnut, CA April 17 vs. Oregon ** Drake Stadium April 22-23 at Triton Invitational La Jolla, CA May 1 at USC Los Angeles, CA May 6-7 at Pac-10 Multi-Event Championships Tucson, AZ May 7 at Oxy Invitational Eagle Rock, CA May 13-14 at Pac-10 Championships Tucson, AZ May 26-27 at NCAA Preliminary Round Eugene, OR June 8-11 at NCAA Outdoor Championships Des Moines, IA ** denotes UCLA home meet TABLE OF CONTENTS/QUICK FACTS QUICK FACTS TABLE OF CONTENTS Location .............................................................................J.D. Morgan Center, GENERAL INFORMATION ..........................................325 Westwood Plaza, Los Angeles, CA, 90095 2011 Schedule .........................Inside Front Cover Athletics Phone ......................................................................(310) -

Teen Sensation Athing Mu
• ALL THE BEST IN RUNNING, JUMPING & THROWING • www.trackandfieldnews.com MAY 2021 The U.S. Outdoor Season Explodes Athing Mu Sets Collegiate 800 Record American Records For DeAnna Price & Keturah Orji T&FN Interview: Shalane Flanagan Special Focus: U.S. Women’s 5000 Scene Hayward Field Finally Makes Its Debut NCAA Formchart Faves: Teen LSU Men, USC Women Sensation Athing Mu Track & Field News The Bible Of The Sport Since 1948 AA WorldWorld Founded by Bert & Cordner Nelson E. GARRY HILL — Editor JANET VITU — Publisher EDITORIAL STAFF Sieg Lindstrom ................. Managing Editor Jeff Hollobaugh ................. Associate Editor BUSINESS STAFF Ed Fox ............................ Publisher Emeritus Wallace Dere ........................Office Manager Teresa Tam ..................................Art Director WORLD RANKINGS COMPILERS Jonathan Berenbom, Richard Hymans, Dave Johnson, Nejat Kök SENIOR EDITORS Bob Bowman (Walking), Roy Conrad (Special AwaitsAwaits You.You. Projects), Bob Hersh (Eastern), Mike Kennedy (HS Girls), Glen McMicken (Lists), Walt Murphy T&FN has operated popular sports tours since 1952 and has (Relays), Jim Rorick (Stats), Jack Shepard (HS Boys) taken more than 22,000 fans to 60 countries on five continents. U.S. CORRESPONDENTS Join us for one (or more) of these great upcoming trips. John Auka, Bob Bettwy, Bret Bloomquist, Tom Casacky, Gene Cherry, Keith Conning, Cheryl Davis, Elliott Denman, Peter Diamond, Charles Fleishman, John Gillespie, Rich Gonzalez, Ed Gordon, Ben Hall, Sean Hartnett, Mike Hubbard, ■ 2022 The U.S. Nationals/World Champion- ■ World Track2023 & Field Championships, Dave Hunter, Tom Jennings, Roger Jennings, Tom ship Trials. Dates and site to be determined, Budapest, Hungary. The 19th edition of the Jordan, Kim Koffman, Don Kopriva, Dan Lilot, but probably Eugene in late June. -

All Time Men's World Ranking Leader
All Time Men’s World Ranking Leader EVER WONDER WHO the overall best performers have been in our authoritative World Rankings for men, which began with the 1947 season? Stats Editor Jim Rorick has pulled together all kinds of numbers for you, scoring the annual Top 10s on a 10-9-8-7-6-5-4-3-2-1 basis. First, in a by-event compilation, you’ll find the leaders in the categories of Most Points, Most Rankings, Most No. 1s and The Top U.S. Scorers (in the World Rankings, not the U.S. Rankings). Following that are the stats on an all-events basis. All the data is as of the end of the 2019 season, including a significant number of recastings based on the many retests that were carried out on old samples and resulted in doping positives. (as of April 13, 2020) Event-By-Event Tabulations 100 METERS Most Points 1. Carl Lewis 123; 2. Asafa Powell 98; 3. Linford Christie 93; 4. Justin Gatlin 90; 5. Usain Bolt 85; 6. Maurice Greene 69; 7. Dennis Mitchell 65; 8. Frank Fredericks 61; 9. Calvin Smith 58; 10. Valeriy Borzov 57. Most Rankings 1. Lewis 16; 2. Powell 13; 3. Christie 12; 4. tie, Fredericks, Gatlin, Mitchell & Smith 10. Consecutive—Lewis 15. Most No. 1s 1. Lewis 6; 2. tie, Bolt & Greene 5; 4. Gatlin 4; 5. tie, Bob Hayes & Bobby Morrow 3. Consecutive—Greene & Lewis 5. 200 METERS Most Points 1. Frank Fredericks 105; 2. Usain Bolt 103; 3. Pietro Mennea 87; 4. Michael Johnson 81; 5.