Applied Statistics in Ecology: Common Pitfalls and Simple Solutions 1, 2 3 4 E
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Statistical Fallacy: a Menace to the Field of Science
International Journal of Scientific and Research Publications, Volume 9, Issue 6, June 2019 297 ISSN 2250-3153 Statistical Fallacy: A Menace to the Field of Science Kalu Emmanuel Ogbonnaya*, Benard Chibuike Okechi**, Benedict Chimezie Nwankwo*** * Department of Ind. Maths and Applied Statistics, Ebonyi State University, Abakaliki ** Department of Psychology, University of Nigeria, Nsukka. *** Department of Psychology and Sociological Studies, Ebonyi State University, Abakaliki DOI: 10.29322/IJSRP.9.06.2019.p9048 http://dx.doi.org/10.29322/IJSRP.9.06.2019.p9048 Abstract- Statistical fallacy has been a menace in the field of easier to understand but when used in a fallacious approach can sciences. This is mostly contributed by the misconception of trick the casual observer into believing something other than analysts and thereby led to the distrust in statistics. This research what the data shows. In some cases, statistical fallacy may be investigated the conception of students from selected accidental or unintentional. In others, it is purposeful and for the departments on statistical concepts as it relates statistical fallacy. benefits of the analyst. Students in Statistics, Economics, Psychology, and The fallacies committed intentionally refer to abuse of Banking/Finance department were randomly sampled with a statistics and the fallacy committed unintentionally refers to sample size of 36, 43, 41 and 38 respectively. A Statistical test misuse of statistics. A misuse occurs when the data or the results was conducted to obtain their conception score about statistical of analysis are unintentionally misinterpreted due to lack of concepts. A null hypothesis which states that there will be no comprehension. The fault cannot be ascribed to statistics; it lies significant difference between the students’ conception of with the user (Indrayan, 2007). -

Misuse of Statistics in Surgical Literature
Statistics Corner Misuse of statistics in surgical literature Matthew S. Thiese1, Brenden Ronna1, Riann B. Robbins2 1Rocky Mountain Center for Occupational & Environment Health, Department of Family and Preventive Medicine, 2Department of Surgery, School of Medicine, University of Utah, Salt Lake City, Utah, USA Correspondence to: Matthew S. Thiese, PhD, MSPH. Rocky Mountain Center for Occupational & Environment Health, Department of Family and Preventive Medicine, School of Medicine, University of Utah, 391 Chipeta Way, Suite C, Salt Lake City, UT 84108, USA. Email: [email protected]. Abstract: Statistical analyses are a key part of biomedical research. Traditionally surgical research has relied upon a few statistical methods for evaluation and interpretation of data to improve clinical practice. As research methods have increased in both rigor and complexity, statistical analyses and interpretation have fallen behind. Some evidence suggests that surgical research studies are being designed and analyzed improperly given the specific study question. The goal of this article is to discuss the complexities of surgical research analyses and interpretation, and provide some resources to aid in these processes. Keywords: Statistical analysis; bias; error; study design Submitted May 03, 2016. Accepted for publication May 19, 2016. doi: 10.21037/jtd.2016.06.46 View this article at: http://dx.doi.org/10.21037/jtd.2016.06.46 Introduction the most commonly used statistical tests of the time (6,7). Statistical methods have since become more complex Research in surgical literature is essential for furthering with a variety of tests and sub-analyses that can be used to knowledge, understanding new clinical questions, as well as interpret, understand and analyze data. -

United Nations Fundamental Principles of Official Statistics
UNITED NATIONS United Nations Fundamental Principles of Official Statistics Implementation Guidelines United Nations Fundamental Principles of Official Statistics Implementation guidelines (Final draft, subject to editing) (January 2015) Table of contents Foreword 3 Introduction 4 PART I: Implementation guidelines for the Fundamental Principles 8 RELEVANCE, IMPARTIALITY AND EQUAL ACCESS 9 PROFESSIONAL STANDARDS, SCIENTIFIC PRINCIPLES, AND PROFESSIONAL ETHICS 22 ACCOUNTABILITY AND TRANSPARENCY 31 PREVENTION OF MISUSE 38 SOURCES OF OFFICIAL STATISTICS 43 CONFIDENTIALITY 51 LEGISLATION 62 NATIONAL COORDINATION 68 USE OF INTERNATIONAL STANDARDS 80 INTERNATIONAL COOPERATION 91 ANNEX 98 Part II: Implementation guidelines on how to ensure independence 99 HOW TO ENSURE INDEPENDENCE 100 UN Fundamental Principles of Official Statistics – Implementation guidelines, 2015 2 Foreword The Fundamental Principles of Official Statistics (FPOS) are a pillar of the Global Statistical System. By enshrining our profound conviction and commitment that offi- cial statistics have to adhere to well-defined professional and scientific standards, they define us as a professional community, reaching across political, economic and cultural borders. They have stood the test of time and remain as relevant today as they were when they were first adopted over twenty years ago. In an appropriate recognition of their significance for all societies, who aspire to shape their own fates in an informed manner, the Fundamental Principles of Official Statistics were adopted on 29 January 2014 at the highest political level as a General Assembly resolution (A/RES/68/261). This is, for us, a moment of great pride, but also of great responsibility and opportunity. In order for the Principles to be more than just a statement of noble intentions, we need to renew our efforts, individually and collectively, to make them the basis of our day-to-day statistical work. -

The Numbers Game - the Use and Misuse of Statistics in Civil Rights Litigation
Volume 23 Issue 1 Article 2 1977 The Numbers Game - The Use and Misuse of Statistics in Civil Rights Litigation Marcy M. Hallock Follow this and additional works at: https://digitalcommons.law.villanova.edu/vlr Part of the Civil Procedure Commons, Civil Rights and Discrimination Commons, Evidence Commons, and the Labor and Employment Law Commons Recommended Citation Marcy M. Hallock, The Numbers Game - The Use and Misuse of Statistics in Civil Rights Litigation, 23 Vill. L. Rev. 5 (1977). Available at: https://digitalcommons.law.villanova.edu/vlr/vol23/iss1/2 This Article is brought to you for free and open access by Villanova University Charles Widger School of Law Digital Repository. It has been accepted for inclusion in Villanova Law Review by an authorized editor of Villanova University Charles Widger School of Law Digital Repository. Hallock: The Numbers Game - The Use and Misuse of Statistics in Civil Righ 1977-19781 THE NUMBERS GAME - THE USE AND MISUSE OF STATISTICS IN CIVIL RIGHTS LITIGATION MARCY M. HALLOCKt I. INTRODUCTION "In the problem of racial discrimination, statistics often tell much, and Courts listen."' "We believe it evident that if the statistics in the instant matter represent less than a shout, they certainly constitute '2 far more than a mere whisper." T HE PARTIES TO ACTIONS BROUGHT UNDER THE CIVIL RIGHTS LAWS3 have relied increasingly upon statistical 4 analyses to establish or rebut cases of unlawful discrimination. Although statistical evidence has been considered significant in actions brought to redress racial discrimination in jury selection,5 it has been used most frequently in cases of allegedly discriminatory t B.A., University of Pennsylvania, 1972; J.D., Georgetown University Law Center, 1975. -
Misuse of Statistics
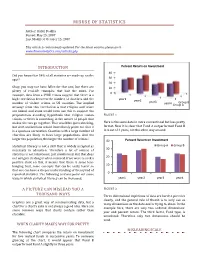
MISUSE OF STATISTICS Author: Rahul Dodhia Posted: May 25, 2007 Last Modified: October 15, 2007 This article is continuously updated. For the latest version, please go to www.RavenAnalytics.com/articles.php INTRODUCTION Percent Return on Investment 40 Did you know that 54% of all statistics are made up on the 30 spot? 20 Okay, you may not have fallen for that one, but there are 10 plenty of real-life examples that bait the mind. For 0 example, data from a 1988 census suggest that there is a high correlation between the number of churches and the year1 year2 number of violent crimes in US counties. The implied year3 Group B year4 Group A message from this correlation is that religion and crime are linked, and some would even use this to support the preposterous sounding hypothesis that religion causes FIGURE 1 crimes, or there is something in the nature of people that makes the two go together. That would be quite shocking, Here is the same data in more conventional but less pretty but alert statisticians would immediately point out that it format. Now it is clear that Fund A outperformed Fund B is a spurious correlation. Counties with a large number of in 3 out of 4 years, not the other way around. churches are likely to have large populations. And the larger the population, the larger the number of crimes.1 40 Percent Return on Investment Statistical literacy is not a skill that is widely accepted as Group A Group B necessary in education. Therefore a lot of misuse of 30 statistics is not intentional, just uninformed. -

Quantifying Aristotle's Fallacies
mathematics Article Quantifying Aristotle’s Fallacies Evangelos Athanassopoulos 1,* and Michael Gr. Voskoglou 2 1 Independent Researcher, Giannakopoulou 39, 27300 Gastouni, Greece 2 Department of Applied Mathematics, Graduate Technological Educational Institute of Western Greece, 22334 Patras, Greece; [email protected] or [email protected] * Correspondence: [email protected] Received: 20 July 2020; Accepted: 18 August 2020; Published: 21 August 2020 Abstract: Fallacies are logically false statements which are often considered to be true. In the “Sophistical Refutations”, the last of his six works on Logic, Aristotle identified the first thirteen of today’s many known fallacies and divided them into linguistic and non-linguistic ones. A serious problem with fallacies is that, due to their bivalent texture, they can under certain conditions disorient the nonexpert. It is, therefore, very useful to quantify each fallacy by determining the “gravity” of its consequences. This is the target of the present work, where for historical and practical reasons—the fallacies are too many to deal with all of them—our attention is restricted to Aristotle’s fallacies only. However, the tools (Probability, Statistics and Fuzzy Logic) and the methods that we use for quantifying Aristotle’s fallacies could be also used for quantifying any other fallacy, which gives the required generality to our study. Keywords: logical fallacies; Aristotle’s fallacies; probability; statistical literacy; critical thinking; fuzzy logic (FL) 1. Introduction Fallacies are logically false statements that are often considered to be true. The first fallacies appeared in the literature simultaneously with the generation of Aristotle’s bivalent Logic. In the “Sophistical Refutations” (Sophistici Elenchi), the last chapter of the collection of his six works on logic—which was named by his followers, the Peripatetics, as “Organon” (Instrument)—the great ancient Greek philosopher identified thirteen fallacies and divided them in two categories, the linguistic and non-linguistic fallacies [1]. -

UNIT 1 INTRODUCTION to STATISTICS Introduction to Statistics
UNIT 1 INTRODUCTION TO STATISTICS Introduction to Statistics Structure 1.0 Introduction 1.1 Objectives 1.2 Meaning of Statistics 1.2.1 Statistics in Singular Sense 1.2.2 Statistics in Plural Sense 1.2.3 Definition of Statistics 1.3 Types of Statistics 1.3.1 On the Basis of Function 1.3.2 On the Basis of Distribution of Data 1.4 Scope and Use of Statistics 1.5 Limitations of Statistics 1.6 Distrust and Misuse of Statistics 1.7 Let Us Sum Up 1.8 Unit End Questions 1.9 Glossary 1.10 Suggested Readings 1.0 INTRODUCTION The word statistics has different meaning to different persons. Knowledge of statistics is applicable in day to day life in different ways. In daily life it means general calculation of items, in railway statistics means the number of trains operating, number of passenger’s freight etc. and so on. Thus statistics is used by people to take decision about the problems on the basis of different type of quantitative and qualitative information available to them. However, in behavioural sciences, the word ‘statistics’ means something different from the common concern of it. Prime function of statistic is to draw statistical inference about population on the basis of available quantitative information. Overall, statistical methods deal with reduction of data to convenient descriptive terms and drawing some inferences from them. This unit focuses on the above aspects of statistics. 1.1 OBJECTIVES After going through this unit, you will be able to: Define the term statistics; Explain the status of statistics; Describe the nature of statistics; State basic concepts used in statistics; and Analyse the uses and misuses of statistics. -

Prestructuring Multilayer Perceptrons Based on Information-Theoretic
Portland State University PDXScholar Dissertations and Theses Dissertations and Theses 1-1-2011 Prestructuring Multilayer Perceptrons based on Information-Theoretic Modeling of a Partido-Alto- based Grammar for Afro-Brazilian Music: Enhanced Generalization and Principles of Parsimony, including an Investigation of Statistical Paradigms Mehmet Vurkaç Portland State University Follow this and additional works at: https://pdxscholar.library.pdx.edu/open_access_etds Let us know how access to this document benefits ou.y Recommended Citation Vurkaç, Mehmet, "Prestructuring Multilayer Perceptrons based on Information-Theoretic Modeling of a Partido-Alto-based Grammar for Afro-Brazilian Music: Enhanced Generalization and Principles of Parsimony, including an Investigation of Statistical Paradigms" (2011). Dissertations and Theses. Paper 384. https://doi.org/10.15760/etd.384 This Dissertation is brought to you for free and open access. It has been accepted for inclusion in Dissertations and Theses by an authorized administrator of PDXScholar. Please contact us if we can make this document more accessible: [email protected]. Prestructuring Multilayer Perceptrons based on Information-Theoretic Modeling of a Partido-Alto -based Grammar for Afro-Brazilian Music: Enhanced Generalization and Principles of Parsimony, including an Investigation of Statistical Paradigms by Mehmet Vurkaç A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Electrical and Computer Engineering Dissertation Committee: George G. Lendaris, Chair Douglas V. Hall Dan Hammerstrom Marek Perkowski Brad Hansen Portland State University ©2011 ABSTRACT The present study shows that prestructuring based on domain knowledge leads to statistically significant generalization-performance improvement in artificial neural networks (NNs) of the multilayer perceptron (MLP) type, specifically in the case of a noisy real-world problem with numerous interacting variables. -

K C Chakrabarty: Uses and Misuses of Statistics
K C Chakrabarty: Uses and misuses of statistics Address by Dr K C Chakrabarty, Deputy Governor of the Reserve Bank of India, at the DST Centre for Interdisciplinary Mathematical Sciences, Faculty of Science, Banaras Hindu University, as part of the 150th Birth Anniversary Celebrations of Mahanama Pandit Madan Mohan Malviya, Varanasi, 20 March 2012. * * * Assistance provided by Shri Abhiman Das in preparation of this address is gratefully acknowledged. 1. Prof. Umesh Singh, Coordinator, DST Centre for Interdisciplinary Mathematical Sciences, Prof Sengupta, Dean Faculty of Science, Prof Joshi, other distinguished members of faculty of the University, and above all, dear students. I thank you all for inviting me to be in your midst during the 150th birth anniversary celebrations of Mahamana Pandit Madan Mohan Malviya. It is a great honour and privilege for me. Pandit Madan Mohan Malviya 2. You have provided an opportunity to me to pay my tribute to the “Mahamana” by delivering a lecture as part of the celebrations of his 150th birth anniversary. He was one of the greatest personalities that this nation has ever produced. In many senses, he was what most of the top class institutions today vie to produce. He was, at the same time a great patriot, an eminent educationist, a teacher of teachers, a silver-tongued transcendental orator, an ancient as well as a modern leader, a reluctant but an eminent lawyer, a social reformer, a great human being, a torch-bearer of the downtrodden, and above all, a great nation builder. He lived his life for us and for the future generations. -

The Quest for Statistical Significance: Ignorance, Bias and Malpractice of Research Practitioners Joshua Abah
The Quest for Statistical Significance: Ignorance, Bias and Malpractice of Research Practitioners Joshua Abah To cite this version: Joshua Abah. The Quest for Statistical Significance: Ignorance, Bias and Malpractice of Research Practitioners. International Journal of Research & Review (www.ijrrjournal.com), 2018, 5 (3), pp.112- 129. hal-01758493 HAL Id: hal-01758493 https://hal.archives-ouvertes.fr/hal-01758493 Submitted on 4 Apr 2018 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Distributed under a Creative Commons Attribution - NonCommercial - ShareAlike| 4.0 International License International Journal of Research and Review www.gkpublication.in E-ISSN: 2349-9788; P-ISSN: 2454-2237 Review Article The Quest for Statistical Significance: Ignorance, Bias and Malpractice of Research Practitioners Joshua Abah Abah Department of Science Education University of Agriculture, Makurdi, Nigeria ABSTRACT There is a growing body of evidence on the prevalence of ignorance, biases and malpractice among researchers which questions the authenticity, validity and integrity of the knowledge been propagated in professional circles. The push for academic relevance and career advancement have driven some research practitioners into committing gross misconduct in the form of innocent ignorance, sloppiness, malicious intent and outright fraud. -

Responsible Use of Statistical Methods Larry Nelson North Carolina State University at Raleigh
University of Massachusetts Amherst ScholarWorks@UMass Amherst Ethics in Science and Engineering National Science, Technology and Society Initiative Clearinghouse 4-1-2000 Responsible Use of Statistical Methods Larry Nelson North Carolina State University at Raleigh Charles Proctor North Carolina State University at Raleigh Cavell Brownie North Carolina State University at Raleigh Follow this and additional works at: https://scholarworks.umass.edu/esence Part of the Engineering Commons, Life Sciences Commons, Medicine and Health Sciences Commons, Physical Sciences and Mathematics Commons, and the Social and Behavioral Sciences Commons Recommended Citation Nelson, Larry; Proctor, Charles; and Brownie, Cavell, "Responsible Use of Statistical Methods" (2000). Ethics in Science and Engineering National Clearinghouse. 301. Retrieved from https://scholarworks.umass.edu/esence/301 This Teaching Module is brought to you for free and open access by the Science, Technology and Society Initiative at ScholarWorks@UMass Amherst. It has been accepted for inclusion in Ethics in Science and Engineering National Clearinghouse by an authorized administrator of ScholarWorks@UMass Amherst. For more information, please contact [email protected]. Responsible Use of Statistical Methods focuses on good statistical practices. In the Introduction we distinguish between two types of activities; one, those involving the study design and protocol (a priori) and two, those actions taken with the results (post hoc.) We note that right practice is right ethics, the distinction between a mistake and misconduct and emphasize the importance of how the central hypothesis is stated. The Central Essay, I dentification of Outliers in a Set of Precision Agriculture Experimental Data by Larry A. Nelson, Charles H. Proctor and Cavell Brownie, is a good paper to study. -

Avoiding Statistical Mistakes Nora Strasser, (E-Mail: [email protected]), Friends University
Journal of College Teaching & Learning – July 2007 Volume 4, Number 7 Avoiding Statistical Mistakes Nora Strasser, (E-mail: [email protected]), Friends University ABSTRACT Avoiding statistical mistakes is important for educators at all levels. Basic concepts will help you to avoid making mistakes using statistics and to look at data with a critical eye. Statistical data is used at educational institutions for many purposes. It can be used to support budget requests, changes in educational philosophy, changes to programs, and addition of new programs. Therefore, it is important to be sure that decisions based on statistical data are valid. Also, it is important to be certain that the data has been presented in a fair and unbiased way. Otherwise, the changes and decisions may not reflect the best interests of the educational institution or its constituents. Many faculty, staff, and administrators at colleges and universities use statistics to support their findings. Most conclusions are based on the data collected and the analysis. If either the data collected or the analysis is faulty, the conclusions may be invalid. Unfortunately, misuses and abuses are common. This paper attempts to present basic concepts that will help you to avoid making mistakes when using statistics and to look at data with a critical eye. No extensive knowledge of mathematics or statistics is needed to be able to judge the validity of the data. The following questions will be answered: How can administrators avoid making invalid decisions when presented with statistical data? And, how can researchers avoid making mistakes that undermine the validity of their data? First, we will look at sources of bias.