UCGE Reports Augmentation of GPS with a Barometer and a Heading
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Fest Face Forward
2013 FESTIVAL GUIDE may • 17 • 13 PUTHeadline Ros atueYO dolent wis am Uauguer alisiR tat fest face FORwaRD Waa-hoo,By it’s Credit time Tktktkttktkt to get your war paint on for festival season! We’ve got 152 of ’em to colour your summer. Connect to your city at More Fun Inside: Mumford & Sons vs. Fleetwood Mac A Late Bloomer Aces the Art Game + + Tom’s House of Pizza Turns 50 2013 FESTIVAL GUIDE PUT YOUR fest face FORWARD To celebrate the start of festival season, we asked a professional face painter to “illustrate” several events on living canvases—the mugs of Swerve staffers and contributors. And we’ve rounded up 152 festivals to colour your spring, summer and fall. face paintings by photographed by LÉ A SELLEY MARC RIMMER “[Adults also] LET’S FACE IT, after want to feel the age of about six, legal opportunities to make minor, joyful spectacles of ourselves are few and far between. special, get (True, Roughriders fans seem to find a way around the noticed, maybe cultural and emotional barriers that prevent the rest of get some good us from embracing our inner jubilant freaks on a regu- lar basis but, well, we can’t all be from Saskatchewan.) vibes bouncing Wouldn’t it be great, though, if every once in a while off of everyone you could, for instance, get a stranger on the bus to look around them.” up from his iPad and smile? Or occasionally inspire the barista taking your coffee order to look directly into your —Léa Selley eyes with a bit of awe and wonder? While we’re not sug- gesting you leave the house in a watermelon helmet, we do think the coming festival season smooths the way for us to surprise, amuse, connect and otherwise jolt each other out of our routines, which can only make us a lighter, loftier, more harmonious bunch the rest of the year. -

Your Ticket to Fun & Savings!
GATE GATE PARK PRICE DISCOUNT PARK PRICE DISCOUNT Discount Ticket Order Form Dorney Park & A$48.99 $15 off Adult. $6 off Child. Order Schlitterbahn Water A$41.16 Multiple ticket savings & ticket options. To order discount tickets, choose from the parks/movie YOUR TICKET TO Wildwater Kingdom C$29.99 online through TicketsAtWork.com Park C$36.46 Visit: schlitterbahn.com/sunclub, Allentown, PA & create an account using the South Padre Island, TX Enter Promotional Code: 777311777 theaters featured in this brochure and list your selections, Company Code BENEFITMS. quantity of tickets and cost* on this form. Hawiian Falls A$24.99 $7 off Adult. $2 off Child. Visit: FUN & SAVINGS! Hershey Park A$55.20 $18.20 off Adult. $8.20 off Child. Order Waco, TX C$19.99 http://store.hfalls.com/store/affiliate *Cost only applies to movie tickets. Hershey, PA C$37.20 online through TicketsAtWork.com join.aspx?affiliatecode=BMS11 & create an account using the Please call 1-800-861-6536 to check ticket avail- Company Code BENEFITMS. Kings Dominion A$59.99 $19 off Adult. $7 off Child. Order Doswell, VA C$37.99 online through TicketsAtWork.com ability before mailing in your order. Follow the rest Sesame Place A$57.99 $6.99 off Adult & Child. Order online & create an account using the of the instructions on this form as indicated. Don’t wait… Langhorne, PA through TicketsAtWork.com Company Code BENEFITMS. & create an account using the Order your discount tickets Company Code BENEFITMS. Ocean Breeze A$31.99 $6.99 off Adult. -

Festival Guide
MAY • 19 • 17 FESTIVAL GUIDE 2017More than 200 events—big, small, downright obscure—are heading this way to enliven your spring, summer and, shudder, fall. It’s time to get busy. FESTIVAL GUIDE 2017 May A Night at the Banff Mountain Film Festival When: Wednesdays and Sundays until May 31, June 16 to Sept. 15 What: Featuring award-winners and audience favour- ites from the annual festival. Where: Lux Cinema, 229 Bear St., Banff, Alta. 1-800- 413-8368, banffcentre.ca. Ginapalooza When: Ongoing until Thursday, June 1 WRAP What: Gin-focused festival celebrating local gin distill- ers, international gin brands and gin cocktails. Where: Various venues. ginapalooza.com. Fairy Tales Queer Film Festival YOUR HEAD When: Friday, May 19 to Saturday, May 27 What: Nine days of LGBTQA programming guaranteed to provoke, challenge and entertain. Now in its 19th season, Fairy Tales features more than 35 screenings of queer film from around the world as well as perfor- AROUND THIS mances, parties and panels. Where: The Plaza Theatre, 1133 Kensington Rd. N.W. Our annual guide to festival season will put you in fairytalesfilmfest.com. Calaway Park Grand-Opening Weekend the centre of the action. It’ll be like the summer When: Saturday, May 20 to Monday, May 22 What: Western Canada’s largest outdoor family revolves around you. amusement park opens for another season of fun. Where: 245033 Range Rd. 33. calawaypark.com. urs is a circular path. The Earth since its inception 28 years ago. Heritage Park Opening Weekend Oaround the sun. The days of the In the course of the 12 years we When: Saturday, May 20 to Monday, May 22 week, months of the year and the have been producing our annual fes- What: The Historical Village opens for its 53rd summer season, offering horse-drawn wagon seasons. -

Annual Report 2019
Annual Report 2019 www.kidsupfront.com/calgary Meet Our Board Chair I joined the Board of Kids Up Front Calgary 10 years ago. After a decade with the organization, I feel just as strongly about its mission as the day I joined. KUF Calgary provides over 30,000 tickets and experiences annually to deserving children and families in Calgary and Southern Alberta. We do this all with a small-but-mighty staff and volunteer Board that go above and beyond each and every day. 2020 is the 20th anniversary of Kids Up Front, and we're looking forward to the celebrations. Ayaz Gulamhussein, Board Chair A Message From Our Executive Director As a registered charity, we strive to make miracles happen while keeping the cost of performing these miracles very low. With support from our caring community, three people make over 30,000 dreams come true every year! The experiences delivered would not be possible if it weren’t for my brilliant team. Thank you, Carissa and Shanon, for your passion, hard work and dedication. You are the reason we continue to see success and make a difference in the lives of deserving kids. A special thanks to Harlee Code and Landon Wesley for their years of dedication and service to Kids Up Front. You will always be a part of the KUF Krew! Our program is one of a kind; it is not redundant, and it complements the important frontline work of our partner agencies. With our unique system of collaboration with 300 social service and community service programs, our reach is broad, diverse, inclusive, and covers communities across Southern Alberta. -

Your Ticket to Fun & Savings!
GATE PARK PRICE DISCOUNT QTY Discount Ticket Order Form $7 off Adult. Visit: Hawiian Falls A$23.99 To order discount tickets, choose from the parks/movie Mansfield, TX C$16.99 https://tickets.hfalls.com/affiliate. YOUR TICKET TO asp?ID=0F7CCEB2-2914-4095-B847- theaters featured in this brochure and list your selections, CDDCE6444C41, Enter store code: BMS11 quantity of tickets and cost* on this form. Schlitterbahn Water Park A$33.99 $3 off Gate ____ *Cost only applies to movie tickets. FUN & SAVINGS! New Braufels, TX C$31.99 Please call 1-800-861-6536 to check ticket avail- Hawiian Falls - The Colony A$23.99 $7 off Adult. Visit: ability before mailing in your order. Follow the rest Plano, TX C$16.99 https://tickets.hfalls.com/affiliate. asp?ID=0F7CCEB2-2914-4095-B847- of the instructions on this form as indicated. Don’t wait… CDDCE6444C41, Enter store code: BMS11 Order your discount tickets Hawiian Falls A$23.99 $7 off Adult. Visit: NAME: __________________________________________ today to your favorite Ronoake, TX C$16.99 https://tickets.hfalls.com/affiliate. asp?ID=0F7CCEB2-2914-4095-B847- CDDCE6444C41, Enter store code: BMS11 ADDRESS: ______________________________________ Theme Parks & Movie Theaters. Sea World A$59.99 $10.50 off Adult. $9.30 off Child. CITY: ___________________________________________ San Antonio, TX C$49.99 Visit: www.commerce.4adventure. com/eStore/scripts/skins/PAW/ Promotion.aspx STATE: _____________ ZIP: _______________________ Six Flags Fiesta Texas A$54.99 $16 off Adult. $9 off Child. Visit: San Antonio, TX C$39.99 https://shopsixflags.accesso.com/ DAYTIME PHONE #: (_________) ____________________ clients/sixflags/affiliate/index.php? m=16534. -

Water Use and Conservation in the CMR Study
REPORT Calgary Metropolitan Region Board Water Use and Conservation in the Calgary Metropolitan Region Study OCTOBER 2019 CONFIDENTIALITY AND © COPYRIGHT This document is for the sole use of the addressee and Associated Engineering Alberta Ltd. The document contains proprietary and confidential information that shall not be reproduced in any manner or disclosed to or discussed with any other parties without the express written permission of Associated Engineering Alberta Ltd. Information in this document is to be considered the intellectual property of Associated Engineering Alberta Ltd. in accordance with Canadian copyright law. This report was prepared by Associated Engineering Alberta Ltd. for the account of Calgary Metropolitan Region Board. The material in it reflects Associated Engineering Alberta Ltd.’s best judgement, in the light of the information available to it, at the time of preparation. Any use which a third party makes of this report, or any reliance on or decisions to be made based on it, are the responsibility of such third parties. Associated Engineering Alberta Ltd. accepts no responsibility for damages, if any, suffered by any third party as a result of decisions made or actions based on this report. Calgary Metropolitan Region Board TABLE OF CONTENTS SECTION PAGE NO. Table of Contents i 1 Introduction 1-1 1.1 Background 1-1 1.2 Project Objective 1-3 1.3 Project Scope of Work 1-3 2 Methodology 2-1 3 Data Collection and Review 3-1 3.1 Water Sources 3-1 3.2 Water Measurement and Consumption 3-5 3.3 Rate Structure 3-8 -

Partners You Make a Difference
cbe.ab.ca partners you make a difference 2012/2013 The Calgary Board of Education is proud to be associated with numerous organizations that support and enhance student learning. In order to meet student needs, our partnerships are highly dynamic, and evolve over time. Following is a list of many of the organizations that work with Calgary Board of Education schools and students, and who contribute to the strength and viability of public education. If your organization supports student learning at the school level, and would like to be included in the list below please contact [email protected] to add your name. Thank you to all the organizations that support Calgary Board of Education students and staff in providing Calgary with a world-class public education system. collaboration agreements other sponsors, donors and partners Calgary Emergency Medical Services Calgary Emergency Women’s Centre Organizations with collaboration agreements 3M Canada Calgary Fire Department provide programs and/or services with CBE schools AADAC Calgary Flames Hockey Club within the required guidelines and regulations. Alberta - Apprenticeship and Training Calgary Foundation Alberta Adolescent Recovery Centre Calgary Herald AWO TAAN Alberta Alcohol and Drug Abuse Commission Calgary Hitmen Hockey Club Big Brothers Big Sisters Alberta Beverage Container Recycling Corporation Calgary Immigrant Aid Society Boys & Girls Clubs of Calgary Alberta Bottle Depot Association Calgary Immigrant Women’s Association Breakfast Club Alberta Children’s Hospital Calgary -

Copyright City of Calgary
PREFACE The City of Calgary Archives is a section of the City Clerk's Department. The Archives was established in 1981. The descriptive system currently in use was established in 1991. The Archives Society of Alberta has endorsed the use of the Bureau of Canadian Archivists' Rules for Archival Description as the standard of archival description to be used in Alberta's archival repositories. In acting upon the recommendations of the Society, the City of Calgary Archives will endeavour to use RAD whenever possible and to subsequently adopt new rules as they are announced by the Bureau. The focus of the City of Calgary Archives' descriptive system is the series level and, consequently, RAD has been adapted to meet the descriptive needs of that level. RAD will eventually be used to describe archival records at the fonds level. The City of Calgary Archives creates inventories of records of private agencies and individuals as the basic structural finding aid to private records. Private records include a broad range of material such as office records of elected municipal officials, records of boards and commissions funded in part or wholly by the City of Calgary, records of other organizations which function at the municipal level, as well as personal papers of individuals. All of these records are collected because of their close relationship to the records of the civic government, and are subject to formal donor agreements. The search pattern for information in private records is to translate inquiries into terms of type of activity, to link activity with agencies which are classified according to activity, to peruse the appropriate inventories to identify pertinent record series, and then to locate these series, or parts thereof, through the location register. -

2015 Annual Report
2015 to the Community to the ANNUAL REPORT LOUGHEED HOUSE NATIONAL & PROVINCIAL HISTORIC SITE & MUSEUM KIRSTIN EVENDEN EXECUTIVE DIRECTOR EXECUTIVE DIRECTOR’S REMARKS 2015 was a special year at Lougheed House as we celebrated our 10th anniversary of Lougheed House National & Provincial Historic Site and our 20th Anniversary of the Lougheed House Conservation Society. These anniversaries were an opportunity to reflect on all that the Society has accomplished in creating and growing Lougheed House as a dynamic cultural hub in the heart of our city. 2015 also marked the first year of our 2015-17 Programming and Strategic Initiatives Plan as we rolled out new opportunities to for the community to be a part of Lougheed House. We continued to evolve our organization to ensure its ongoing sustainability, in a time of economic uncertainty in Alberta. As a non-profit organization responsible for ensuring Lougheed House continues to thrive in the future, we raised approximately 41% of revenues through fundraising, donations, earned income and grants. We managed our expenses carefully, invested in key priorities, sourced new development revenues, and pursued a new fundraising initiative. This past year we also continued to reach out to the community to seek feedback on what our visitors want to see when they visit and engage with Lougheed House. Lougheed House works closely with a number of partners to maintain and care for the Historic Site and we are grateful to the Government of Alberta, a key stakeholder and supporter in the care and operation of Lougheed House through the Ministry of Culture and Tourism, and the Ministry of Infrastructure. -

Sharing Your Inner Child
BIG BROTHERS BIG SISTERS OF CALGARY AND AREA SHARING YOUR INNER CHILD Annual Report 2011/12 SHARING SWEET MOMENTS AMANDA and KAYLA MATCHED 1 YEAR Little Sister Kayla was both shy and excited about meeting Big Sister Amanda at Thomas B. Riley School in September. Matched through the mPower Youth Mentoring program, the two quickly became friends. Amanda and Kayla enjoy their weekly hour together with an array of activities, from crafts, cooking, and learning to just plain girly stuff. One day, Amanda brought in her curling iron to fancy Kayla’s locks. Right in the middle of styling, they were interrupted by a fire drill. “We had to go outside with half Kayla’s hair curled and half on top of her head. Her friends thought it was pretty cool she was getting her hair done at school.” Having a Big Sister like Amanda really makes Kayla feel special. “I can tell her anything and trust her. She gets me.” Amanda brings a nurturing side and lends an ear whenever it’s needed. “The program enables me to be someone who listens first and gives Kayla a sense that someone is going to be there for her. I’ve seen a lot of growth in Kayla. It’s been really cool to see her develop more confidence and better problem solving skills.” The duo will say farewell for the summer, pocketing their memories until they meet again in the fall. SHARING YOUR LOVE OF LAUGHTER ROBB, CEILIDH and CORY MATCHED 5 YEARS Big Brother Robb and Little Brother Cory met on a bright August day in 2007, both excited to share their laughter and do “things only kids should be doing.” They first tackled the nearest playground, then quenched their thirst with drinks from a nearby convenience store. -
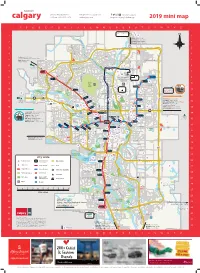
2019 Mini Map
phone: 403-263-8510 [email protected] /tourismcalgary toll free: 1-800-661-1678 visitcalgary.com #capturecalgary | #askmeyyc 2019 mini map A B C D E F G H I J K L M N O P Q R S T U V W X Y Z ? 1 58 10 1 Airdrie 13 km / 8 miles SY MON Drumheller 117 km / 73 miles S VA L Red Deer 128 km / 80 miles 2 L 2 E Y Edmonton 278 km / 173 miles 144 AV NW R S D H A N G W A 3 N #201 W #201 E STONEY TR NE 3 A P P K I E T E R R C N E W S O R 4 T 4 N T O FO Cochrane 17 km / 10 miles ER W E to Yamnuska Wolfdog Sanctuary 31 km / 19 miles EST D 13 NO 5 S 5 Banff (alternate route) E COUNTRY HILLS BV NE C 117 km / 73 miles R TR E E K 6 36 ST NE 6 43 ARLOW 96 B Spring Hill RV Park AV NE 300 NW 300 300 27 km / 17 miles COUNTRY HILLS BV 300 AIRPORT TRAIL (96 AV NE) TUNNEL 7 Tuscany BEDDINGT 62 7 W 44 ST NE N R ON ? 300 W T TR N I NOSE HILL DR P P R 300 80 AV NE Saddletowne T A 8 8 N YYC CALGARY Y A E Crowfoot 14 ST NW 300 G N TR NW INTERNATIONAL A O H T R Martindale S S AIRPORT 60 T CRO S SARCEE NOSE I 9 WCHILD T 9 300 Deerfoot E HILL City M 64 AV NE TR NW McKnight/ PARK 64 AV NE Westwinds t 66 r o JOHN LA 10 rp Dalhousie 10 BO i W R A I o V t BOWNESS URIE BV 300 ER E 29 14 1 PARK McKNIGHT BV 0 2 11 Calaway Park # 50 McKNIGHT BV 11 6 km / 4 miles 33 40 Hangar Flight 300 Museum 36 ST NE Brentwood Chestermere 8 km / 5 miles Calgary West Canada’s CF 34 Whitehorn Calaway RV Park Campground Market N Sports O DEERFOO Strathmore 38 km / 24 miles 12 & Campground Mall 12 Hall of Fame 19 University S 72 32 AV NE Dinosaur Prov. -

DECEMBER 2019 Price : $1.25
DECEMBER 2019 price : $1.25 R E Y COVER Calgary & Southern Alberta Meeting Directory ALCOHOLICS ANONYMOUS CENTRAL SERVICE OFFICE #2, 4015 – 1st Street S.E. (access off 39th Avenue from Macleod Trail S.) Calgary, Alberta T2G 4X7 phone : 403-777-1212 e-mail : [email protected] website: www.calgaryaa.org OFFICE HOURS Monday to Friday : 8:30 a.m. – 5:00 p.m. (Closed for lunch, 1:00 p.m. – 2:00 p.m.) Saturdays : 9:00 a.m. – 1:00 p.m. (Closed Holiday Weekends) Area 78 (Alta./N.W.T.) website : www.area78.org General Service Office (New York) website : www.aa.org INDEX Group Index ................................................................................... 3, 4 Meetings Held Daily (Mon. – Fri.) .................................................. 5, 6 Calgary Weekly Meetings ............................................................. 6–24 Spanish Speaking Meetings ............. 6, 10, 11, 12, 14, 16, 17, 18, 20, 22 Polish Speaking Meeting ................................................................. 13 Punjabi/Hindi speaking meetings ..................................................... 21 Hospital and Treatment Facility Meetings ....................................... 24 Intergroup & General Service Committee Mtgs ............................... 25 Out of Town Meetings ............................................................... 25–35 Central Office Support & Suggested Group Contributions .............. 36 12 Steps & 12 Traditions ............................................................ 37, 38 The 20 Questions (Are