DOCSLIB.ORG

Tropical Geometry, OMT and Neural Network

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Tropical Geometry, OMT and Neural Network Tropical Geometry, OMT and Neural Network Na Lei1 1DUT-RU International School of Information Sciences and Engineering Dalian University of Technology Geometric Analysis Approach to AI CMSA, Harvard 2019-01-22 Na Lei ([email protected]) (DLUT) Tropical Geometry, OMT and NN 01/22/2019 1 / 62 Thanks Thanks for the invitation. Na Lei ([email protected]) (DLUT) Tropical Geometry, OMT and NN 01/22/2019 2 / 62 Collaborators This is a joint work with Professor David Xianfeng Gu, Zhongxuan Luo, Lianbao Jin, Hao wang and so on. Na Lei ([email protected]) (DLUT) Tropical Geometry, OMT and NN 01/22/2019 3 / 62 Outline 1 Introduction to Tropical Geometry 2 Tropical Geometry for Neural Network 3 Optimal Transport Mapping 4 OMT by Neural Network Na Lei ([email protected]) (DLUT) Tropical Geometry, OMT and NN 01/22/2019 4 / 62 Introduction to Tropical Geometry Na Lei ([email protected]) (DLUT) Tropical Geometry, OMT and NN 01/22/2019 5 / 62 Tropical Algebra Tropical geometry is based on tropical semiring. Tropical semiring 1 Tropical Addition: ; ⊕ 2 Tropical Multiplication: ; 3 Tropical semiring: T := (R ¥ ; ; ). [ {− g ⊕ Tropical semiring is also known as the max-plus algebra. Na Lei ([email protected]) (DLUT) Tropical Geometry, OMT and NN 01/22/2019 6 / 62 Tropical Algebra Tropical operators For x;y R, 2 1 their tropical sum is x y := max x;y ; ⊕ f g 2 their tropical product is x y := x + y; 3 the tropical quotient of x over y is x y := x y. − ¥ x = x = 0 x; ¥ x = ¥: − ⊕ − − ¥: the tropical additive identity, 0: the tropical multiplicative identity. − Associativity, Commutativity, Distributivity. Lack of additive inverse. T := (R ¥ ; ; ) is a semiring. [ {− g ⊕ Na Lei ([email protected]) (DLUT) Tropical Geometry, OMT and NN 01/22/2019 7 / 62 Tropical Algebra Tropical operators For x;y R, 2 1 their tropical sum is x y := max x;y ; ⊕ f g 2 their tropical product is x y := x + y; 3 the tropical quotient of x over y is x y := x y. − ¥ x = x = 0 x; ¥ x = ¥: − ⊕ − − ¥: the tropical additive identity, 0: the tropical multiplicative identity. − Associativity, Commutativity, Distributivity. Lack of additive inverse. T := (R ¥ ; ; ) is a semiring. [ {− g ⊕ Na Lei ([email protected]) (DLUT) Tropical Geometry, OMT and NN 01/22/2019 7 / 62 Tropical Algebra Tropical operators For x;y R, 2 1 their tropical sum is x y := max x;y ; ⊕ f g 2 their tropical product is x y := x + y; 3 the tropical quotient of x over y is x y := x y. − ¥ x = x = 0 x; ¥ x = ¥: − ⊕ − − ¥: the tropical additive identity, 0: the tropical multiplicative identity. − Associativity, Commutativity, Distributivity. Lack of additive inverse. T := (R ¥ ; ; ) is a semiring. [ {− g ⊕ Na Lei ([email protected]) (DLUT) Tropical Geometry, OMT and NN 01/22/2019 7 / 62 Tropical Algebra Tropical operators For x;y R, 2 1 their tropical sum is x y := max x;y ; ⊕ f g 2 their tropical product is x y := x + y; 3 the tropical quotient of x over y is x y := x y. − ¥ x = x = 0 x; ¥ x = ¥: − ⊕ − − ¥: the tropical additive identity, 0: the tropical multiplicative identity. − Associativity, Commutativity, Distributivity. Lack of additive inverse. T := (R ¥ ; ; ) is a semiring. [ {− g ⊕ Na Lei ([email protected]) (DLUT) Tropical Geometry, OMT and NN 01/22/2019 7 / 62 Tropical Algebra Tropical power Let N = n Z : n 0 . For any integer a N, raising x R to the a th power: f 2 ≥ g 2 2 − a x := x x = a x ··· · where the last denotes standard product of real numbers. · For any a N, 2 ( a ¥ if a > 0; ¥ := − − 0 if a = 0: Every x R has a tropical multiplicative inverse given by its standard additive2 inverse: 1 x − := x: − Thus T is in fact a semifield. Na Lei ([email protected]) (DLUT) Tropical Geometry, OMT and NN 01/22/2019 8 / 62 Tropical Algebra Tropical power Let N = n Z : n 0 . For any integer a N, raising x R to the a th power: f 2 ≥ g 2 2 − a x := x x = a x ··· · where the last denotes standard product of real numbers. · For any a N, 2 ( a ¥ if a > 0; ¥ := − − 0 if a = 0: Every x R has a tropical multiplicative inverse given by its standard additive2 inverse: 1 x − := x: − Thus T is in fact a semifield. Na Lei ([email protected]) (DLUT) Tropical Geometry, OMT and NN 01/22/2019 8 / 62 Tropical Algebra One may therefore also raise x R to a negative power a Z by raising its tropical multiplicative2 inverse x to the positive power2 a, i.e., x a = ( x) a. − − − − ¥ does not have a tropical multiplicative inverse and ( ¥) a is − − undefined for a < 0. Na Lei ([email protected]) (DLUT) Tropical Geometry, OMT and NN 01/22/2019 9 / 62 Tropical Algebra One may therefore also raise x R to a negative power a Z by raising its tropical multiplicative2 inverse x to the positive power2 a, i.e., x a = ( x) a. − − − − ¥ does not have a tropical multiplicative inverse and ( ¥) a is − − undefined for a < 0. Na Lei ([email protected]) (DLUT) Tropical Geometry, OMT and NN 01/22/2019 9 / 62 Tropical Algebra Tropical monomial A tropical monomial in d variables x1;:::;xd is an expression of the form a a a ad cx = c x 1 x 2 x 1 2 ··· d d where c R ¥ , a1;:::;ad N, a = (a1;:::;ad ) N and 2 [ {− g 2 2 x = (x1;:::;xd ). Note that xa = 0 xa as 0 is the tropical multiplicative identity. A tropical monomial is indeed a linear function, or equivalently, a hyperplane: a x + a x + + a x + c: 1 1 2 2 ··· d d Na Lei ([email protected]) (DLUT) Tropical Geometry, OMT and NN 01/22/2019 10 / 62 Tropical Algebra Tropical monomial A tropical monomial in d variables x1;:::;xd is an expression of the form a a a ad cx = c x 1 x 2 x 1 2 ··· d d where c R ¥ , a1;:::;ad N, a = (a1;:::;ad ) N and 2 [ {− g 2 2 x = (x1;:::;xd ). Note that xa = 0 xa as 0 is the tropical multiplicative identity. A tropical monomial is indeed a linear function, or equivalently, a hyperplane: a x + a x + + a x + c: 1 1 2 2 ··· d d Na Lei ([email protected]) (DLUT) Tropical Geometry, OMT and NN 01/22/2019 10 / 62 Tropical Algebra Tropical polynomial A tropical polynomial f (x) = f (x1;:::;xd ) is a finite tropical sum of tropical monomials a1 ar f (x) = c x cr x ; 1 ⊕ ··· ⊕ d where ci R ¥ and ai = (ai1; ;aid ) N for i = 1; ;r: 2 [ {− g ··· 2 ··· A monomial of a given multiindex appears at most once in the sum, i.e., a = a for any i = j. i 6 j 6 A tropical polynomial is indeed a piecewise linear function, or equivalently, an upper envelope of the r hyperplanes: maxr a x + a x + + a x + c : i=1f i1 1 i2 2 ··· id d i g Na Lei ([email protected]) (DLUT) Tropical Geometry, OMT and NN 01/22/2019 11 / 62 Tropical Algebra Tropical polynomial A tropical polynomial f (x) = f (x1;:::;xd ) is a finite tropical sum of tropical monomials a1 ar f (x) = c x cr x ; 1 ⊕ ··· ⊕ d where ci R ¥ and ai = (ai1; ;aid ) N for i = 1; ;r: 2 [ {− g ··· 2 ··· A monomial of a given multiindex appears at most once in the sum, i.e., a = a for any i = j. i 6 j 6 A tropical polynomial is indeed a piecewise linear function, or equivalently, an upper envelope of the r hyperplanes: maxr a x + a x + + a x + c : i=1f i1 1 i2 2 ··· id d i g Na Lei ([email protected]) (DLUT) Tropical Geometry, OMT and NN 01/22/2019 11 / 62 Tropical Algebra Tropical rational function A tropical rational function is a standard difference, or, equivalently, a tropical quotient of two tropical polynomials f (x) and g(x): f (x) g(x) = f (x) g(x): − The set of tropical polynomials T[x1;:::;xd ] forms a semiring under the standard extension of and to tropical polynomials, and likewise the ⊕ set of tropical rational functions T(x1;:::;xd ) forms a semifield. We regard a tropical polynomial f = f 0 as a special cases of a tropical rational function and thus T[x1;:::;xd ] T(x1;:::;xd ): ⊆ Na Lei ([email protected]) (DLUT) Tropical Geometry, OMT and NN 01/22/2019 12 / 62 Tropical Algebra Tropical rational function A tropical rational function is a standard difference, or, equivalently, a tropical quotient of two tropical polynomials f (x) and g(x): f (x) g(x) = f (x) g(x): − The set of tropical polynomials T[x1;:::;xd ] forms a semiring under the standard extension of and to tropical polynomials, and likewise the ⊕ set of tropical rational functions T(x1;:::;xd ) forms a semifield. We regard a tropical polynomial f = f 0 as a special cases of a tropical rational function and thus T[x1;:::;xd ] T(x1;:::;xd ): ⊆ Na Lei ([email protected]) (DLUT) Tropical Geometry, OMT and NN 01/22/2019 12 / 62 Tropical Algebra Tropical rational function A tropical rational function is a standard difference, or, equivalently, a tropical quotient of two tropical polynomials f (x) and g(x): f (x) g(x) = f (x) g(x): − The set of tropical polynomials T[x1;:::;xd ] forms a semiring under the standard extension of and to tropical polynomials, and likewise the ⊕ set of tropical rational functions T(x1;:::;xd ) forms a semifield.
Load more

Recommended publications
  • Tropical Geometry of Deep Neural Networks
    Tropical Geometry of Deep Neural Networks Liwen Zhang 1 Gregory Naitzat 2 Lek-Heng Lim 2 3 Abstract 2011; Montufar et al., 2014; Eldan & Shamir, 2016; Poole et al., 2016; Telgarsky, 2016; Arora et al., 2018). Recent We establish, for the first time, explicit connec- work (Zhang et al., 2016) showed that several successful tions between feedforward neural networks with neural networks possess a high representation power and ReLU activation and tropical geometry — we can easily shatter random data. However, they also general- show that the family of such neural networks is ize well to data unseen during training stage, suggesting that equivalent to the family of tropical rational maps. such networks may have some implicit regularization. Tra- Among other things, we deduce that feedforward ditional measures of complexity such as VC-dimension and ReLU neural networks with one hidden layer can Rademacher complexity fail to explain this phenomenon. be characterized by zonotopes, which serve as Understanding this implicit regularization that begets the building blocks for deeper networks; we relate generalization power of deep neural networks remains a decision boundaries of such neural networks to challenge. tropical hypersurfaces, a major object of study in tropical geometry; and we prove that linear The goal of our work is to establish connections between regions of such neural networks correspond to neural network and tropical geometry in the hope that they vertices of polytopes associated with tropical ra- will shed light on the workings of deep neural networks. tional functions. An insight from our tropical for- Tropical geometry is a new area in algebraic geometry that mulation is that a deeper network is exponentially has seen an explosive growth in the recent decade but re- more expressive than a shallow network.
    [Show full text]
  • Group Actions and Divisors on Tropical Curves Max B
    Claremont Colleges Scholarship @ Claremont HMC Senior Theses HMC Student Scholarship 2011 Group Actions and Divisors on Tropical Curves Max B. Kutler Harvey Mudd College Recommended Citation Kutler, Max B., "Group Actions and Divisors on Tropical Curves" (2011). HMC Senior Theses. 5. https://scholarship.claremont.edu/hmc_theses/5 This Open Access Senior Thesis is brought to you for free and open access by the HMC Student Scholarship at Scholarship @ Claremont. It has been accepted for inclusion in HMC Senior Theses by an authorized administrator of Scholarship @ Claremont. For more information, please contact [email protected]. Group Actions and Divisors on Tropical Curves Max B. Kutler Dagan Karp, Advisor Eric Katz, Reader May, 2011 Department of Mathematics Copyright c 2011 Max B. Kutler. The author grants Harvey Mudd College and the Claremont Colleges Library the nonexclusive right to make this work available for noncommercial, educational purposes, provided that this copyright statement appears on the reproduced ma- terials and notice is given that the copying is by permission of the author. To dis- seminate otherwise or to republish requires written permission from the author. Abstract Tropical geometry is algebraic geometry over the tropical semiring, or min- plus algebra. In this thesis, I discuss the basic geometry of plane tropical curves. By introducing the notion of abstract tropical curves, I am able to pass to a more abstract metric-topological setting. In this setting, I discuss divisors on tropical curves. I begin a study of G-invariant divisors and divisor classes. Contents Abstract iii Acknowledgments ix 1 Tropical Geometry 1 1.1 The Tropical Semiring .
    [Show full text]
  • Notes by Eric Katz TROPICAL GEOMETRY
    Notes by Eric Katz TROPICAL GEOMETRY GRIGORY MIKHALKIN 1. Introduction 1.1. Two applications. Let us begin with two examples of questions where trop- ical geometry is useful. Example 1.1. Can we represent an untied trefoil knot as a genus 1 curve of degree 5 in RP3? Yes, by means of tropical geometry. It turns out that it can be be represented by a rational degree 5 curve but not by curve of genus greater than 1 since such a curve must sit on a quadric surface in RP3. 3 k 3 Figure 1. Untied trefoil. Example 1.2. Can we enumerate real and complex curves simultaneously by com- binatorics? For example, there is a way to count curves in RP2 or CP2 through 3d − 1+ g points by using bipartite graphs. 1.2. Tropical Geometry. Tropical geometry is algebraic geometry over the tropi- cal semi-field, (T, “+”, “·”). The semi-field’s underlying set is the half-open interval [−∞, ∞). The operations are given for a,b ∈ T by “a + b” = max(a,b) “a · b”= a + b. The semi-field has the properties of a field except that additive inverses do not exist. Moreover, every element is an idempotent, “a + a”= a so there is no way to adjoin inverses. In some sense algebra becomes harder, geometry becomes easier. By the way, tropical geometry is named in honor of a Brazilian computer scien- tist, Imre Simon. Two observations make tropical geometry easy. First, the tropical semiring T naturally has a Euclidean topology like R and C. Second, the geometric structures are piecewise linear structures, and so tropical geometry reduces to a combination 1 2 MIKHALKIN of combinatorics and linear algebra.
    [Show full text]
  • Applications of Tropical Geometry in Deep Neural Networks
    Applications of Tropical Geometry in Deep Neural Networks Thesis by Motasem H. A. Alfarra In Partial Fulfillment of the Requirements For the Degree of Masters of Science in Electrical Engineering King Abdullah University of Science and Technology Thuwal, Kingdom of Saudi Arabia April, 2020 2 EXAMINATION COMMITTEE PAGE The thesis of Motasem H. A. Alfarra is approved by the examination committee Committee Chairperson: Bernard S. Ghanem Committee Members: Bernard S. Ghanem, Wolfgang Heidrich, Xiangliang Zhang 3 ©April, 2020 Motasem H. A. Alfarra All Rights Reserved 4 ABSTRACT Applications of Tropical Geometry in Deep Neural Networks Motasem H. A. Alfarra This thesis tackles the problem of understanding deep neural network with piece- wise linear activation functions. We leverage tropical geometry, a relatively new field in algebraic geometry to characterize the decision boundaries of a single hidden layer neural network. This characterization is leveraged to understand, and reformulate three interesting applications related to deep neural network. First, we give a geo- metrical demonstration of the behaviour of the lottery ticket hypothesis. Moreover, we deploy the geometrical characterization of the decision boundaries to reformulate the network pruning problem. This new formulation aims to prune network pa- rameters that are not contributing to the geometrical representation of the decision boundaries. In addition, we propose a dual view of adversarial attack that tackles both designing perturbations to the input image, and the equivalent perturbation to the decision boundaries. 5 ACKNOWLEDGEMENTS First of all, I would like to express my deepest gratitude to my thesis advisor Prof. Bernard Ghanem who supported me through this journey. Prof.
    [Show full text]
  • Tropical Geometry? Eric Katz Communicated by Cesar E
    THE GRADUATE STUDENT SECTION WHAT IS… Tropical Geometry? Eric Katz Communicated by Cesar E. Silva This note was written to answer the question, What is tropical geometry? That question can be interpreted in two ways: Would you tell me something about this research area? and Why the unusual name ‘tropi- Tropical cal geometry’? To address Figure 1. Tropical curves, such as this tropical line the second question, trop- and two tropical conics, are polyhedral complexes. geometry ical geometry is named in transforms honor of Brazilian com- science. Here, tropical geometry can be considered as alge- puter scientist Imre Simon. braic geometry over the tropical semifield (ℝ∪{∞}, ⊕, ⊗) questions about This naming is compli- with operations given by cated by the fact that he algebraic lived in São Paolo and com- 푎 ⊕ 푏 = min(푎, 푏), 푎 ⊗ 푏 = 푎 + 푏. muted across the Tropic One can then find tropical analogues of classical math- varieties into of Capricorn. Whether his ematics and define tropical polynomials, tropical hyper- work is tropical depends surfaces, and tropical varieties. For example, a degree 2 questions about on whether he preferred to polynomial in variables 푥, 푦 would be of the form do his research at home or polyhedral min(푎 + 2푥, 푎 + 푥 + 푦, 푎 + 2푦, 푎 + 푥, 푎 + 푦, 푎 ) in the office. 20 11 02 10 01 00 complexes. The main goal of for constants 푎푖푗 ∈ ℝ ∪ {∞}. The zero locus of a tropical tropical geometry is trans- polynomial is defined to be the set of points where the forming questions about minimum is achieved by at least two entries.
    [Show full text]
  • The Boardman Vogt Resolution and Tropical Moduli Spaces
    The Boardman Vogt resolution and tropical moduli spaces by Nina Otter Master Thesis submitted to The Department of Mathematics Supervisors: Prof. Dr. John Baez (UCR) Prof. Dr. Giovanni Felder (ETH) Contents Page Acknowledgements 5 Introduction 7 Preliminaries 9 1. Monoidal categories 9 2. Operads 13 3. Trees 17 Operads and homotopy theory 31 4. Monoidal model categories 31 5. A model structure on the category of topological operads 32 6. The W-construction 35 Tropical moduli spaces 41 7. Abstract tropical curves as metric graphs 47 8. Tropical modifications and pointed curves 48 9. Tropical moduli spaces 49 Appendix A. Closed monoidal categories, enrichment and the endomorphism operad 55 Appendix. Bibliography 63 3 Acknowledgements First and foremost I would like to thank Professor John Baez for making this thesis possible, for his enduring patience and support, and for sharing his lucid vision of the big picture, sparing me the agony of mindlessly hacking my way through the rainforest of topological operads and possibly falling victim to the many perils which lurk within. Furthermore I am indebted to Professor Giovanni Felder who kindly assumed the respon- sibility of supervising the thesis on behalf of the ETH, and for several fruitful meetings in which he took time to listen to my progress, sharing his clear insight and giving precious advice. I would also like to thank David Speyer who pointed out the relation between tropical geometry and phylogenetic trees to Professor Baez, and Adrian Clough for all the fruitful discussions on various topics in this thesis and for sharing his ideas on mathematical writing in general.
    [Show full text]
  • Tropical Geometry to Analyse Demand
    TROPICAL GEOMETRY TO ANALYSE DEMAND Elizabeth Baldwin∗ and Paul Klemperery preliminary draft May 2012, slightly revised July 2012 The latest version of this paper and related material will be at http://users.ox.ac.uk/∼wadh1180/ and www.paulklemperer.org ABSTRACT Duality techniques from convex geometry, extended by the recently-developed math- ematics of tropical geometry, provide a powerful lens to study demand. Any consumer's preferences can be represented as a tropical hypersurface in price space. Examining the hypersurface quickly reveals whether preferences represent substitutes, complements, \strong substitutes", etc. We propose a new framework for understanding demand which both incorporates existing definitions, and permits additional distinctions. The theory of tropical intersection multiplicities yields necessary and sufficient conditions for the existence of a competitive equilibrium for indivisible goods{our theorem both en- compasses and extends existing results. Similar analysis underpins Klemperer's (2008) Product-Mix Auction, introduced by the Bank of England in the financial crisis. JEL nos: Keywords: Acknowledgements to be completed later ∗Balliol College, Oxford University, England. [email protected] yNuffield College, Oxford University, England. [email protected] 1 1 Introduction This paper introduces a new way to think about economic agents' individual and aggregate demands for indivisible goods,1 and provides a new set of geometric tools to use for this. Economists mostly think about agents'
    [Show full text]
  • The Enumerative Geometry of Rational and Elliptic Tropical Curves and a Riemann-Roch Theorem in Tropical Geometry
    The enumerative geometry of rational and elliptic tropical curves and a Riemann-Roch theorem in tropical geometry Michael Kerber Am Fachbereich Mathematik der Technischen Universit¨atKaiserslautern zur Verleihung des akademischen Grades Doktor der Naturwissenschaften (Doctor rerum naturalium, Dr. rer. nat.) vorgelegte Dissertation 1. Gutachter: Prof. Dr. Andreas Gathmann 2. Gutachter: Prof. Dr. Ilia Itenberg Abstract: The work is devoted to the study of tropical curves with emphasis on their enumerative geometry. Major results include a conceptual proof of the fact that the number of rational tropical plane curves interpolating an appropriate number of general points is independent of the choice of points, the computation of intersection products of Psi- classes on the moduli space of rational tropical curves, a computation of the number of tropical elliptic plane curves of given genus and fixed tropical j-invariant as well as a tropical analogue of the Riemann-Roch theorem for algebraic curves. Mathematics Subject Classification (MSC 2000): 14N35 Gromov-Witten invariants, quantum cohomology 51M20 Polyhedra and polytopes; regular figures, division of spaces 14N10 Enumerative problems (combinatorial problems) Keywords: Tropical geometry, tropical curves, enumerative geometry, metric graphs. dedicated to my parents — in love and gratitude Contents Preface iii Tropical geometry . iii Complex enumerative geometry and tropical curves . iv Results . v Chapter Synopsis . vi Publication of the results . vii Financial support . vii Acknowledgements . vii 1 Moduli spaces of rational tropical curves and maps 1 1.1 Tropical fans . 2 1.2 The space of rational curves . 9 1.3 Intersection products of tropical Psi-classes . 16 1.4 Moduli spaces of rational tropical maps .
    [Show full text]
  • Product-Mix Auctions and Tropical Geometry
    PRODUCT-MIX AUCTIONS AND TROPICAL GEOMETRY NGOC MAI TRAN AND JOSEPHINE YU Abstract. In a recent and ongoing work, Baldwin and Klemperer explored a con- nection between tropical geometry and economics. They gave a sufficient condition for the existence of competitive equilibrium in product-mix auctions of indivisible goods. This result, which we call the Unimodularity Theorem, can also be traced back to the work of Danilov, Koshevoy, and Murota in discrete convex analysis. We give a new proof of the Unimodularity Theorem via the classical unimodularity theorem in integer programming. We give a unified treatment of these results via tropical geometry and formulate a new sufficient condition for competitive equilib- rium when there are only two types of product. Generalizations of our theorem in higher dimensions are equivalent to various forms of the Oda conjecture in algebraic geometry. 1. Introduction. An auction is a mechanism to sell goods. It is a process that takes in a collection of bids and produces a set of winners, the amount of goods each winner gets, and the prices the winners have to pay. A product-mix auction is a sealed bid, static auction for differentiated goods. That is, no one knows others' bids, each agent submits the bids only once, and there are different types of goods. The goods are said to be indivisible if they can only be sold in integer quantities, and this is the case that interests us. Each agent (bidder) indicates her valuation, or how much each bundle of goods is worth to her. After seeing the bids, the economist sets the per-unit price for each type of good, splits up the supply into possibly empty bundles, one for each agent.
    [Show full text]
  • Tropical Gaussians: a Brief Survey 3
    TROPICAL GAUSSIANS: A BRIEF SURVEY NGOC MAI TRAN Abstract. We review the existing analogues of the Gaussian measure in the tropical semir- ing and outline various research directions. 1. Introduction Tropical mathematics has found many applications in both pure and applied areas, as documented by a growing number of monographs on its interactions with various other ar- eas of mathematics: algebraic geometry [BP16, Gro11, Huh16, MS15], discrete event systems [BCOQ92, But10], large deviations and calculus of variations [KM97, Puh01], and combinato- rial optimization [Jos14]. At the same time, new applications are emerging in phylogenetics [LMY18, YZZ19, PYZ20], statistics [Hoo17], economics [BK19, CT16, EVDD04, GMS13, Jos17, Shi15, Tra13, TY19], game theory, and complexity theory [ABGJ18, AGG12]. There is a growing need for a systematic study of probability distributions in tropical settings. Over the classical algebra, the Gaussian measure is arguably the most important distribution to both theoretical probability and applied statistics. In this work, we review the existing analogues of the Gaussian measure in the tropical semiring. We focus on the three main characterizations of the classical Gaussians central to statistics: invariance under orthonor- mal transformations, independence and orthogonality, and stability. We show that some notions do not yield satisfactory generalizations, others yield the classical geometric or ex- ponential distributions, while yet others yield completely different distributions. There is no single notion of a ‘tropical Gaussian measure’ that would satisfy multiple tropical analogues of the different characterizations of the classical Gaussians. This is somewhat expected, for the interaction between geometry and algebra over the tropical semiring is rather different from that over R.
    [Show full text]
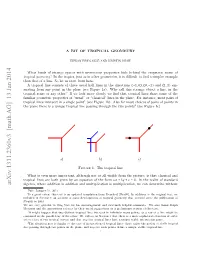
  • A Bit of Tropical Geometry
    A BIT OF TROPICAL GEOMETRY ERWAN BRUGALLE´ AND KRISTIN SHAW What kinds of strange spaces with mysterious properties hide behind the enigmatic name of tropical geometry? In the tropics, just as in other geometries, it is difficult to find a simpler example than that of a line. So let us start from here. A tropical line consists of three usual half lines in the directions 1; 0 ; 0; 1 and 1; 1 em- anating from any point in the plane (see Figure 1a). Why call this strange object a line, in the tropical sense or any other? If we look more closely we find that tropical(− ) lines( − share) some( of) the familiar geometric properties of \usual" or \classical" lines in the plane. For instance, most pairs of tropical lines intersect in a single point1 (see Figure 1b). Also for most choices of pairs of points in the plane there is a unique tropical line passing through the two points2 (see Figure 1c). a) b) c) Figure 1. The tropical line What is even more important, although not at all visible from the picture, is that classical and tropical lines are both given by an equation of the form ax by c 0. In the realm of standard arXiv:1311.2360v3 [math.AG] 13 Jan 2014 algebra, where addition is addition and multiplication is multiplication, we can determine without + + = Date: January 14, 2014. To a great extent this text is an updated translation from French of [Bru09]. In addition to the original text, we included in Section 6 an account of some developments of tropical geometry that occured since the publication of [Bru09] in 2009.
    [Show full text]
  • Combinatorics and Computations in Tropical Mathematics by Bo Lin A
    Combinatorics and Computations in Tropical Mathematics by Bo Lin A dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Mathematics in the Graduate Division of the University of California, Berkeley Committee in charge: Professor Bernd Sturmfels, Chair Professor James Demmel Professor Haiyan Huang Summer 2017 Combinatorics and Computations in Tropical Mathematics Copyright 2017 by Bo Lin 1 Abstract Combinatorics and Computations in Tropical Mathematics by Bo Lin Doctor of Philosophy in Mathematics University of California, Berkeley Professor Bernd Sturmfels, Chair In recent decades, tropical mathematics gradually evolved as a field of study in mathematics and it has more and more interactions with other fields and applications. In this thesis we solve combinatorial and computational problems concerning implicitization, linear systems and phylogenetic trees using tools and results from tropical mathematics. In Chapter 1 we briefly introduce basic aspects of tropical mathematics, including trop- ical arithmetic, tropical polynomials and varieties, and the relationship between tropical geometry and phylogenetic trees. In Chapter 2 we solve the implicitization problem for almost-toric hypersurfaces using results from tropical geometry. With results about the tropicalization of varieties, we present and prove a formula for the Newton polytopes of almost-toric hypersurfaces. This leads to a linear algebra approach for solving the implicitization problem. We implement our algorithm and show that it has better solving ability than some existing methods. In Chapter 3 we compute linear systems on metric graphs. In algebraic geometry, linear systems on curves have been well-studied in the literature. In comparison, linear systems on metric graphs are their counterparts in tropical mathematics.
    [Show full text]