January 1954 TPJ3U of CONTENTS
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
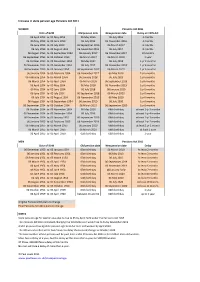
How Has Your State Pension Age Changed?
Increase in state pension age Pensions Act 2011 WOMEN Pensions Act 2011 Date of Birth Old pension date New pension date Delay on 1995 Act 06 April 1953 to 05 May 1953 06 May 2016 06 July 2016 2 months 06 May 1953 to 05 June 1953 06 July 2016 06 November 2016 4 months 06 June 1953 to 05 July 1953 06 September 2016 06 March 2017 6 months 06 July 1953 to 05 August 1953 06 November 2016 06 July 2017 8 months 06 August 1953 to 05 September 1953 06 January 2017 06 November 2017 10 months 06 September 1953 to 05 October 1953 06 March 2017 06 March 2018 1 year 06 October 1953 to 05 November 1953 06 May 2017 06 July 2018 1 yr 2 months 06 November 1953 to 05 December 1953 06 July 2017 06 November 2018 1 yr 4 months 06 December 1953 to 05 January 1954 06 September 2017 06 March 2019 1 yr 6 months 06 January 1954 to 05 February 1954 06 November 2017 06 May 2019 1yr 6 months 06 February 1954 to 05 March 1954 06 January 2018 06 July 2019 1yr 6 months 06 March 1954 to 05 April 1954 06 March 2018 06 September 2019 1yr 6 months 06 April 1954 to 05 May 1954 06 May 2018 06 November 2019 1yr 6 months 06 May 1954 to 05 June 1954 06 July 2018 08 January 2020 1yr 6 months 06 June 1954 to 05 July 1954 06 September 2018 06 March 2020 1yr 6 months 06 July 1954 to 05 August 1954 06 November 2018 06 May 2020 1yr 6 months 06 August 1954 to 05 September 1954 06 January 2019 06 July 2020 1yr 6 months 06 September 1954 to 05 October 1954 06 March 2019 06 September 2020 1yr 6 months 06 October 1954 to 05 November 1954 06 May 2019 66th birthday at least 1 yr 5 months 06 -

Business Conditions: January 1956
A review by the Federal Reserve Bank of Chicago Business Conditions 1956 January Contents The economic consequences of the baby boom 4 The price picture, pressures building up? 8 What they’re saying — about farm prospects, 1956 12 The Trend of Business 2-4 Digitized for FRASER http://fraser.stlouisfed.org/ Federal Reserve Bank of St. Louis the Trend OF BUSINESS R ising business activity during 1955 re having unemployment at less than 1.5 per cent. quired steady additions to the nation’s work Interestingly, the only two cities in the force. During the fourth quarter an average District considered to have a substantial labor of about 51 million persons were on business surplus are South Bend and Terre Haute. These payrolls—almost 1.8 million more than a year cities are located in the same state as Indian earlier and a new record. As a result, in many apolis, Fort Wayne and the Gary-Hammond areas pockets of unemployment continued to portion of the Chicago metropolitan area, all melt through the year. of which report very tight labor markets. This Early in 1956 a seasonal reversal in the situation reflects the tendency for jobs and employment upswing is inevitable. Just as workers to get out of balance in local areas and December almost invariably records the em the reluctance of workers to seek work at a ployment high for the year, as hirings rise to distance from their homes and former jobs. accommodate Christmas business, so do Jan In November some types of manufacturers uary and February mark low points. -
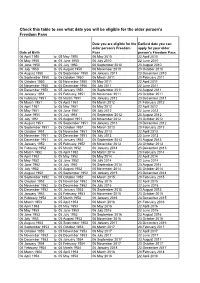
Copy of Age Eligibility from 6 April 10
Check this table to see what date you will be eligible for the older person's Freedom Pass Date you are eligible for the Earliest date you can older person's Freedom apply for your older Date of Birth Pass person's Freedom Pass 06 April 1950 to 05 May 1950 06 May 2010 22 April 2010 06 May 1950 to 05 June 1950 06 July 2010 22 June 2010 06 June 1950 to 05 July 1950 06 September 2010 23 August 2010 06 July 1950 to 05 August 1950 06 November 2010 23 October 2010 06 August 1950 to 05 September 1950 06 January 2011 23 December 2010 06 September 1950 to 05 October 1950 06 March 2011 20 February 2011 06 October 1950 to 05 November 1950 06 May 2011 22 April 2011 06 November 1950 to 05 December 1950 06 July 2011 22 June 2011 06 December 1950 to 05 January 1951 06 September 2011 23 August 2011 06 January 1951 to 05 February 1951 06 November 2011 23 October 2011 06 February 1951 to 05 March 1951 06 January 2012 23 December 2011 06 March 1951 to 05 April 1951 06 March 2012 21 February 2012 06 April 1951 to 05 May 1951 06 May 2012 22 April 2012 06 May 1951 to 05 June 1951 06 July 2012 22 June 2012 06 June 1951 to 05 July 1951 06 September 2012 23 August 2012 06 July 1951 to 05 August 1951 06 November 2012 23 October 2012 06 August 1951 to 05 September 1951 06 January 2013 23 December 2012 06 September 1951 to 05 October 1951 06 March 2013 20 February 2013 06 October 1951 to 05 November 1951 06 May 2013 22 April 2013 06 November 1951 to 05 December 1951 06 July 2013 22 June 2013 06 December 1951 to 05 January 1952 06 September 2013 23 August 2013 06 -

Country Term # of Terms Total Years on the Council Presidencies # Of
Country Term # of Total Presidencies # of terms years on Presidencies the Council Elected Members Algeria 3 6 4 2004 - 2005 December 2004 1 1988 - 1989 May 1988, August 1989 2 1968 - 1969 July 1968 1 Angola 2 4 2 2015 – 2016 March 2016 1 2003 - 2004 November 2003 1 Argentina 9 18 15 2013 - 2014 August 2013, October 2014 2 2005 - 2006 January 2005, March 2006 2 1999 - 2000 February 2000 1 1994 - 1995 January 1995 1 1987 - 1988 March 1987, June 1988 2 1971 - 1972 March 1971, July 1972 2 1966 - 1967 January 1967 1 1959 - 1960 May 1959, April 1960 2 1948 - 1949 November 1948, November 1949 2 Australia 5 10 10 2013 - 2014 September 2013, November 2014 2 1985 - 1986 November 1985 1 1973 - 1974 October 1973, December 1974 2 1956 - 1957 June 1956, June 1957 2 1946 - 1947 February 1946, January 1947, December 1947 3 Austria 3 6 4 2009 - 2010 November 2009 1 1991 - 1992 March 1991, May 1992 2 1973 - 1974 November 1973 1 Azerbaijan 1 2 2 2012 - 2013 May 2012, October 2013 2 Bahrain 1 2 1 1998 - 1999 December 1998 1 Bangladesh 2 4 3 2000 - 2001 March 2000, June 2001 2 Country Term # of Total Presidencies # of terms years on Presidencies the Council 1979 - 1980 October 1979 1 Belarus1 1 2 1 1974 - 1975 January 1975 1 Belgium 5 10 11 2007 - 2008 June 2007, August 2008 2 1991 - 1992 April 1991, June 1992 2 1971 - 1972 April 1971, August 1972 2 1955 - 1956 July 1955, July 1956 2 1947 - 1948 February 1947, January 1948, December 1948 3 Benin 2 4 3 2004 - 2005 February 2005 1 1976 - 1977 March 1976, May 1977 2 Bolivia 3 6 7 2017 - 2018 June 2017, October -

NATO in the Beholder's Eye: Soviet Perceptions and Policies, 1949-1956
WOODROW WILSON INTERNATIONAL CENTER FOR SCHOLARS Christian Ostermann, Lee H. Hamilton, NATO in the Beholder’s Eye: Director Director Soviet Perceptions and Policies, 1949-56 BOARD OF ADVISORY TRUSTEES: COMMITTEE: Vojtech Mastny Joseph A. Cari, Jr., William Taubman Chairman (Amherst College) Steven Alan Bennett, Working Paper No. 35 Chairman Vice Chairman PUBLIC MEMBERS Michael Beschloss (Historian, Author) The Secretary of State Colin Powell; The Librarian of James H. Billington Congress (Librarian of Congress) James H. Billington; The Archivist of the United States Warren I. Cohen John W. Carlin; (University of Maryland- The Chairman of the Baltimore) National Endowment for the Humanities Bruce Cole; John Lewis Gaddis The Secretary of the (Yale University) Smithsonian Institution Lawrence M. Small; The Secretary of James Hershberg Education (The George Washington Roderick R. Paige; University) The Secretary of Health & Human Services Tommy G. Thompson; Samuel F. Wells, Jr. (Woodrow Wilson PRIVATE MEMBERS Washington, D.C. Center) Carol Cartwright, John H. Foster, March 2002 Sharon Wolchik Jean L. Hennessey, (The George Washington Daniel L. Lamaute, University) Doris O. Mausui, Thomas R. Reedy, Nancy M. Zirkin COLD WAR INTERNATIONAL HISTORY PROJECT THE COLD WAR INTERNATIONAL HISTORY PROJECT WORKING PAPER SERIES CHRISTIAN F. OSTERMANN, Series Editor This paper is one of a series of Working Papers published by the Cold War International History Project of the Woodrow Wilson International Center for Scholars in Washington, D.C. Established in 1991 by a grant from the John D. and Catherine T. MacArthur Foundation, the Cold War International History Project (CWIHP) disseminates new information and perspectives on the history of the Cold War as it emerges from previously inaccessible sources on “the other side” of the post-World War II superpower rivalry. -

Tennessee State Library and Archives 403 Seventh Avenue North Nashville, Tennessee 37243-0312
State of Tennessee Department of State Tennessee State Library and Archives 403 Seventh Avenue North Nashville, Tennessee 37243-0312 Ralph G. Morrissey (1903-1956) Papers, 1930 -1956 Processed by: Theodore Morrison, Jr. Accession Number: THS 721 Location: THS VI-E-5 Date: April 29, 1994 Microfilm Accession No.: 1453 The Ralph Morrissey Papers, 1930-1956, centers on Ralph Morrissey (1903- 1956) of Nashville, Tennessee, amateur photographer and newspaper literary review editor. The Ralph Morrissey Papers are a gift of Mrs. Eleanor Morrissey. Single photocopies of unpublished writings in the Ralph Morrissey Papers may be made for scholarly research. Cubic feet of shelf space occupied: 4.58 cu. ft. Approximate number of items: ca. 300; 10 vols. SCOPE AND CONTENT NOTE The Ralph Morrissey Papers contain 10 volumes and approximately 300 items spanning the period between 1930 and 1957. The collection is composed of accounts, an advertisement, clippings, correspondence, invitations, programs, lists, notes, a poem, photographs, press releases, publications, and school records. The bulk of the collection consists of clippings from The Nashville Tennessean featuring the literary review columns of Ralph Morrissey (1903-1956). Included within the correspondence are letters from notables such as Margaret Mitchell, Merrill Moore, Arna Bontemps, Anya Seton, and T.S. Stribling. An avid amateur photographer, Morrissey received numerous national awards. Included in the photographs section of the addition are several of his award- winning shots (see also the Ralph Morrissey Photograph Collection, ac. no. THS 484). Morrissey also garnered awards for his philatelic collection and became well-known as an aficionado of pipes and Sherlock Holmes mysteries. -

January 1954
ALUMNI HOMECOMING ON MAY 21, 22 Drew-Bear to Attend Mark it on Your Calendar American Alumni Council And Save the Date! Conference The 500 Alumni who attend Your Alumni Secretary attended ed last year's reunion had a the annual conference of the Ameri- wonderful time. This year we can Alumni Council at Smith College, expect Alumni to visit the [T orthamptnn, M::t~~ ., nn J an, lO - I~ , Campus in even greater num About 125 persons professionally en bers on May 21, 22. gaged in alumni work at universities and colleges in the New England States, Quebec, the Maritime Prov- . ~ {I' inces and Newfoundland were in Five Year Plan attendance. Participating were James S. Coles, President, Bowdoin Col To Be Repeated lege; John S. Dickey, President, Dartmouth College; Benjamin F. Preparations arc underway for the Wright, President, Smith College; ]954 May Homecoming. The "Five Francis Keppel, Dean of the Gradu- Year Anniversary Plan" will be con ate School of Education, Harvard tinued and a special effort will be University; Miss J eanette McPherrin, made to round up the classes of '53, Kirk Smith Dean of Fres hmen, VVell es ley College. '49, '44, '39, '34, '29, '24, '19, and '14. In addition to its traditional features, NEW TRUSTEE this year's program will include enter ELECTED tainment of unusual sparkle and va A Message from riety. Circle Friday and Saturday, At the Annual Meeting of the May 21 and 22 on your calendar. This Board of Trustees of Bryant College The President promises to be a memorable occasion. -

1954 to December 31,1954
Annual Report of the UNITED STATES COURT OF MILITARY APPEALS and THE JUDGE ADVOCATES GENERAL of the ARMED FORCES and the GENERAL COUNSEL of the DEPARTMENT OF THE TREASURY PURSUANT TO THE UNIFORM CODE OF MILITARY JUSTICE For the Period January 1,1954 to December 31,1954 PROPERTY OF U, S. ARMY ^ THE JUDGE ADYOCATE GENERAL'S SCHOOK LIBRARY Annual Report SUBMITTED TO THE COMMITTEES ON ARMED SERVICES ol the SENATE AND OF THE HOUSE OF REPRESENTATIVES and to the SECRETARY OF DEFENSE m— and the SECRETARIES OF THE DEPARTMENTS OF THE ARMY, NAVY, AIR FORCE, AND TREASURY PURSUANT TO THE UNIFORM CODE OF MILITARY JUSTICE For the Period ' ( - January 1 ,1954 to December 31,1954 r y #* m 3 Contents JOINT REPORT OF THE UNITED STATES COURT OF MILITARY APPEALS AND THE JUDGE ADVOCATES GENERAL OF THE ARMED FORCES AND THE GENERAL COUNSEL OF THE DEPARTMENT OF THE TREASURY REPORT OF THE UNITED STATES COURT OF MILITARY APPEALS REPORT OF THE JUDGE ADVOCATE GENERAL OF THE ARMY REPORT OF THE JUDGE ADVOCATE GENERAL OF THE NAVY REPORT OF THE JUDGE ADVOCATE GENERAL OF THE AIR FORCE REPORT OF THE GENERAL COUNSEL OF THE DEPARTMENT OF THE TREASURY (UNITED STATES COAST GUARD) iii M / \ y " Joint Report of the UNITED STATES COURT OF MILITARY APPEALS and THE JUDGE ADVOCATES GENERAL OF THE ARMED FORCES and THE GENERAL COUNSEL OF THE DEPARTMENT OF THE TREASURY January 1, 1954 to December 31,1954 f t V JOINT REPORT The following report, covering the period from January 1, 1954 through December 31, 1954, is the third report of the Committee created by Article 67 (ff) of the Uniform Code of Military Justice, 50 U. -

ECSC 5Th GR Summary 1957.Pdf
EUBoPEAIT COAI AND STEET COMMUNIIY i* rl il j.I, Sc$$ .- Lihrary SU'MMARY OF THM T'IFIH {NNUAL GENERAL nEP0RI ON IEE ACTIWTII]S Otr' TE]I }IIGH AUTEOE.ISY to be laid before the Connon Assenbly at iis 0rCinar;' Session in Strasbourg on May I4r L9j7 " TUXEMBOURG Aprj:. t957 Lihrar$ hnd i I zp9-4hrc . ,. - - "-. !.r--.I] e i! ii -1- INTRODUCTION t I. This special issue of the tiigh Authorityrs roonthly information bulletin is d.evote,l to s srunnsry of the General Report rrublished. each year, in accordance vrith the Treaty, one mcntir before the Ord.ina.ry Session of the Coruorr Asserubl;,r. 2, &e_041+I!-.1gf,:.rsjg!.1sn_!o_ gp3lr--9._Ug.y_ 14 _1-Ir__Q-!-IgEboqry_ w.tll !q bhe tast be'i'q*qg. tl-r9-911,r.ry...L{ l}e jjrgEiqigIL__:'e_f&4_!g_gire xwlLi.g]-Ui8s--si!!r---tls intrr:duction of the Conunon Ma,rllet .f or co?L oLI sb-UL}!l{[- ]:q.r_I.9Jfu It has been up to the High Authorlty to exanine its record overhhe trarrsition pcriorl; it has hacl- to as}< itself hol.: far the forecasts have been borne out by the factsu a.nd. how far the mach.inery i-nstil,uted. has proclucocl results; it has obviously been obliged. to ';al.;e into account -bile inportance for the build.ing of Europe of such outc'i;andin;:: events as the fremlng: and signature of tire Treaties eotablislring the European Econoinic Co'rnrnuirity and the European Atomic )inergy Coruriuni-',;y. Airtl the resu-ll,s of its self-questionin,g on the progress it has made, ancl of its corrsidera,tir:n of the new conditlons in which it now has to do its worir, tl:c iLigh Authority l:as s,rught to r.,:rnbo0y in i'r;s Gerreral Report. -

EMERGENCY PREPAREDNESS, OFFICE OF: Printed Material, 1953-61
DWIGHT D. EISENHOWER LIBRARY ABILENE, KANSAS EMERGENCY PREPAREDNESS, OFFICE OF: Printed Material, 1953-61 Accession A75-26 Processed by: TB Date Completed: December 1991 This collection was received from the Office of Emergency Preparedness, via the National Archives, in March 1975. No restrictions were placed on the material. Linear feet of shelf space occupied: 5.2 Approximate number of pages: 10,400 Approximate number of items: 6,000 SCOPE AND CONTENT NOTE This collection consists of printed material that was collected for reference purposes by the staff of the Office of Defense Mobilization (ODM) and the Office of Civil and Defense Mobilization (OCDM). The material was inherited by the Office of Emergency Preparedness (OEP), a successor agency to ODM and OCDM. After the OEP was abolished in 1973 the material was turned over to the National Archives and was then sent to the Eisenhower Library. The printed material consists mostly of press releases and public reports that were issued by the White House during the Eisenhower administration. These items are arranged in chronological order by date of release. Additional sets of the press releases are in the Kevin McCann records and in the records of the White House Office, Office of the Press Secretary. Copies of the reports are also in the White House Central Files. The collection also contained several books, periodicals and Congressional committee prints. These items have been transferred to the Eisenhower Library book collection. CONTAINER LIST Box No. Contents 1 Items Transferred -

NSA Newsletter, January 1954
the NSh cl-ieukaul CJenetal J<a~k 1- Canine :J)italct, J1Jauoual ~«Utiftt cA!effC~ Many of us know our Director, Lieutenant General Canine, and have read biographical data in previous Agency publications. He served with the US Army Expeditionary Forces in France during World War I. Among other assignments, he served as Chief of Staff of the XII Corps during World War II in General George s. Patton's Third Army, and later as Deputy Assistant Chief of Staff, G-2, Department of the Army, -in Washington. Since his assignment as Director in July 1951, General Canine has been constantly striving for more and better improve ments in OUl' working c·onditions. His outstanding leadership has been and continues to be an inspiration to each of us. ~proved for Release by NSA on 11-07-2005, FOIA Case # 47295 • -~ # ~", .. ~~~.,.t~~,_._"", January, 1954 no. 3 Washington, D. C. LETTEH Df APPHECI ATION Secret8ry of Defense Charles E. Wilson sent the following letter of Rppreciation to CFlptRin Gullett, USN, the Community Chest C8.rnp::Jign Division Chair man at NSS. (lI am appreciative of your efforts in I he recent Community Chest Campaign. Your participation was very helpful in bringing to f he attention of the person nel of the Defense Dep:lTtment the worth-while pur poses of the Chest Camp:lign. "In this way, funds aTe solicited for many agen cies which are necessary in our community life, to benefit the aged and the young, aid the sick and dis tressed, and provide for the physical and moral train ing of our youth. -

Judgement No. 56
Jodgement No. 56 283 It should be noted that in so doing the Applicant refers to the absence of any examination of his position and the inadequacy of the efforts made to find him employment. The Tribunal, having already dealt with these two points, does not consider it necessary to institute the inquiry requested by the Applicant. Whatever the results of such an inquiry, the Tribunal does not see how they could affect the conclusions set forth in paragraphs 6 and 9 above. 13. For these reasons the Tribunal, while noting the failure to comply with an obligation under the Regulations, is bound to dismiss the application, there being no necessary legal connexion between such failure and the decision to terminate the Applicant. (Signatures) Suzanne BASTID Sture PETRBN Djalal ABDOH President Vice-President Member Omar LOUTFI Mani SANASEN Alternate Member Executive Secretary New York, 14 December 1954 Judgement No. 56 Case No. 58 : Against: The Secretary-General Aglion of the United Nations THE ADMINISTRATIVE TRIBUNAL OF THE UNITED NATIONS. Composed of Madame Paul Bastid, President; Mr. Sture Pet&, Vice-President ; Mr. Jacob Mark Lashly ; Dr. Djalal Abdoh, alternate ; Whereas Raoul Aglion, Resident Representative of the Technical Assistance Board at Port-au-Prince, Haiti, filed an application to the Tribunal on 23 August 1954 requesting: (a) The rescission of the Secretary-General’s decision of 3 April 1952 terminating the Applicant for abolition of post ; (b) The revalidation of the terms of the permanent appointment then improperly terminated