DOCSLIB.ORG

Ada Lovelace's Calculation of Bernoulli's Numbers 1. Introduction

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Ada Lovelace's Calculation of Bernoulli's Numbers 1. Introduction Ada Lovelace's Calculation of Bernoulli's Numbers Ada Lovelace's Calculation of Bernoulli's Numbers Rainer Glaschick, Paderborn, Germany ([email protected]) http://rclab.de/analyticalengine/ 2016-09-29 1. Introduction In 1843, an article with the title Sketch of the Analytical Engine… [ML1843] was published, that contains an extensive and on its level fairly complete description of Charles Babbage's plans for a fully automatic computing engine. Its name has been motivated by the aim that it should be able to numerically solve all computations in the field of mathematical analysis (p.688): … all the Operations of analysis come within the domain of the engine. The article consists of a translation of a report by L.F. Menabrea, originally written in French, and supplements designated as Note A to Note G. The author was Augusta Ada King, Countess of Lovelace, who signed the Notes not by name, only with her initials A.A.L. — for the reasons her biographies should be consulted, that are also the place to the never-ending discussion about her mathematical ability, while this article strongly supports her excellence. The closing Note G got much attention, because the corresponding table now is regarded the first fairly complex program ever. The use of machine instructions, variables and a conditional loop is easily seen; but it is instructive to look into the very details of the program — which few people might have done, not only because several typos are not widely known (the most complete and reliable source seems to be [MCK1989], in particular see p. 159, ft), but also because the program needs a feature, that was not considered in the engine at the time the article was written. Probably this was more clearly seen by Ada Lovelace than by Babbage himself. There are strong indications that the machine could not simply overwrite variables, never explicitely mentioned but implicitely honored by Ada Lovelace as well as Charles Babbage, and, as known so far, not obeyed by all that did build an emulator. The reader should be very careful not to take things for granted that are common today; nearly everybody, myself definitely included, had to find out that he did so at some place. This concerns in particular the assumption that variables can be easily overwritten, and that operation cards are used to perform an operation, once the operands are loaded. 2. The Analytical Engine As no Analytical Engine was ever built, there is no such thing as the Analytical Engine. The plans were continuously modified and improved; and because there was never an attempt to build at least a small prototype, there was no motivation to fix a design. Nevertheless, plans 16, 25 and 28 could be seen as milestones. Plan 25 is dated from 1840 and probably closest to the concept that Babbage introduced in Turin and which was the basis for the work of Menabrea and thus Ada Lovelace. That version was also 1 von 18 29.09.2016 08:12 Ada Lovelace's Calculation of Bernoulli's Numbers engraved and given away by Babbage; it is today the most used graphical view. Loops are not present and are only found in Plan 28 from 1845 (see Bromley in [AB2000], p.6 bottom to p.7 top), significantly later than Ada Lovelace's article. The article is obviously on a generic level and not specifically linked to a certain version. E.g. it is not mentioned that a machine according to Plan 25 would produce a double precision result for a multiplication, thus the operations were not just the plain four given in the article. In fact the nature of the machine is presented by examples, without presenting the model of the machine explicitly. That would not have been possible anyhow, as the concept of the Analytical Engine was completely new and no terminology existed for it. For today's reader, however, that is familiar with electronic computers, the hypothetical machine can be sketched coarsely. It will be called an abstract machine, as it is an abstraction from various plans, and, as is the principle for abstract machines, omit several technical details. 2.1. The abstract Analytical Engine The abstract Engine implied by Ada Lovelace has: a calculating unit (the mill) for the four basic calculations a storage unit (the store) for holding numeric values in variables, also called columns a control unit, using punched cards for programming A calculation step transfers two operands from the store to the mill, calculates the result, and sends it back to the store. Selection of the operands and the operation was done by different punched cards. It follows that normally one operation card and three variable cards were used, two for reading the operands and one for storing the result. To understand Note G, a three-address-machine with four operations is sufficient: Vx + Vy -> Vr Vx - Vy -> Vr Vx × Vy -> Vr Vx ÷ Vy -> Vr where Vx and Vy are the operand variables and Vr is the variable of the result. In the example of the Bernoulli numbers in Note G operations are repeated in a loop, but the mechanism is not explained. The Table only contains a descriptive text and no symbolic indication. To allow this, a conditional repetition, that goes back a predefined number of operations and variable cards if the result in the mill is not zero, is written as: ? ≠ 0 : => k The letter k represents the number of the operation that shall be executed next, although a real machine would use the number of cards to rewind. Note that Menabrea wrote (S.685): These new cards may follow the first, but may only come into play contingently upon one or other of the two circumstances just mentioned taking place. and refers to zero-crossings and overflows, that allow to activate alternative program 2 von 18 29.09.2016 08:12 Ada Lovelace's Calculation of Bernoulli's Numbers parts. According to the current knowledge, there were no plans for loops and conditional jumps of a maturity similar to the arithmetic operations, so that the above conditional backward jump must be seen as very generic. Note that using Jaquard cards for weaving, only a linear sequence is used; all repeats are unraveled, which explains the enormous number of cards cited in the article. 3. The program To demonstrate the exceptional power of the Analytical Engine, the last example in Note G explains the calculation of Bernoulli's numbers. They were probably well known to every professional mathematician, as Ada Lovelace does not bother to explain them or motivate their use. For today's readers, additional information is contained in the appendix. To follow the next chapters, this information is not necessary, if the reader just accepts the equations given. The example in Note G is preceeded by simpler ones, starting by calculating the two unknowns from the six coefficients in two equations, already in the translated part on p. 681, i.e. also in the french original written by Menabrea, which corresponds to unpublished notes by Babbage [CB1837] dated 1837. While these documents still need in-depth analysis, the first impression is that the tables used by Menabrea and Lovelace contain more information than Babbage's ones. Nevertheless, the first simple program ever was written down by Babbage and published by Menabrea; and it shows the sequential control of calculations by cards as well as the reuse of intermediate values, the latter being the primary motivation of Babbage to abandon the Difference Engine. However, the example in Note G is much closer to what we consider a non-trivial computer program today. 3.1. The calculations Starting point for the example are several equations for different methods to calculate Bernoulli's numbers. The equations are marked (1.) to (4.) in the article. The article claims that the second one is well known, but presumably all were common knowledge for mathematicians of that time (a question that might be studied separately), because the finally used equation (8.) is rewritten from the fourth. It was chosen for the illustration of the powers of the engine; moreover, it is the only one that does not use an infinite series and thus avoids discussions on termination and accuracy. Formula (8.) reads: 1 2푛 − 1 2푛 2푛 ⋅ (2푛 − 1) ⋅ (2푛 − 2) 0 = − ⋅ + 퐵1 + 퐵3 2 2푛 + 1 2 2 ⋅ 3 ⋅ 4 2푛 ⋅ (2푛 − 1) ⋅ (2⎜⎛푛 − 2⎟⎞) ⋅ (2푛 −� 3) ⋅ (2푛 − 4) � +퐵5 ⎝ ⎠ + ... + 퐵2푛−1 2 ⋅ 3 ⋅ 4 ⋅ 5 ⋅ 6 � � Evidently it allows, as noted in the article, to calculate 퐵2푛−1, once all previous 퐵2푖−1 have already been calculated. For this purpose, equation (8.) is represented as: 0 = 퐴0(푛) + 퐴1(푛) ⋅ 퐵1 + 퐴3(푛) ⋅ 퐵3 + ... + 퐴2푛−3(푛) ⋅ 퐵2푛−3 + 퐵2푛−1 3 von 18 29.09.2016 08:12 Ada Lovelace's Calculation of Bernoulli's Numbers The above notation differs from equation (9.) in the article, in that the remark in the article that A1, A3 &c. being … functions of n … is made explicit using functional notation. Thus the coefficients are (not given in this form in the article): 1 2푛 − 1 퐴0(푛) = − ⋅ 2 2푛 + 1 2푛 퐴1(푛) = 2 2푛 − 1 2푛 − 2 퐴3(푛) = 퐴1(푛) ⋅ ⋅ 3 4 2푛 − 3 2푛 − 4 퐴5(푛) = 퐴3(푛) ⋅ ⋅ 5 6 For a given 푛, the values can be calculated from already calculated ones of the same 푛, with the significant difference to Bernoulli's numbers, that only the last one is needed and only for the current round. So the equation for the next of Bernoulli's numbers has the finally used form: −퐵2푛−1 = 퐴0(푛) + 퐴1(푛) ⋅ 퐵1 + 퐴3(푛) ⋅ 퐵3 + ..
Load more

Recommended publications
  • Analytical Engine, 1838 ALLAN G
    Charles Babbage’s Analytical Engine, 1838 ALLAN G. BROMLEY Charles Babbage commenced work on the design of the Analytical Engine in 1834 following the collapse of the project to build the Difference Engine. His ideas evolved rapidly, and by 1838 most of the important concepts used in his later designs were established. This paper introduces the design of the Analytical Engine as it stood in early 1838, concentrating on the overall functional organization of the mill (or central processing portion) and the methods generally used for the basic arithmetic operations of multiplication, division, and signed addition. The paper describes the working of the mechanisms that Babbage devised for storing, transferring, and adding numbers and how they were organized together by the “microprogrammed” control system; the paper also introduces the facilities provided for user- level programming. The intention of the paper is to show that an automatic computing machine could be built using mechanical devices, and that Babbage’s designs provide both an effective set of basic mechanisms and a workable organization of a complete machine. Categories and Subject Descriptors: K.2 [History of Computing]- C. Babbage, hardware, software General Terms: Design Additional Key Words and Phrases: Analytical Engine 1. Introduction 1838. During this period Babbage appears to have made no attempt to construct the Analytical Engine, Charles Babbage commenced work on the design of but preferred the unfettered intellectual exploration of the Analytical Engine shortly after the collapse in 1833 the concepts he was evolving. of the lo-year project to build the Difference Engine. After 1849 Babbage ceased designing calculating He was at the time 42 years o1d.l devices.
    [Show full text]
  • Ada Lovelace the first Computer Programmer 1815 - 1852
    Ada Lovelace The first computer programmer 1815 - 1852 Biography Ada Lovelace Day I Born on December 10th, 1815 in London as Augusta Ada Byron Each second Tuesday in October is Ada Lovelace Day. A day to raise the I Parents separated when she was a baby profile of women in science, technology, engineering, and maths to create new role models for girls and women in these fields. During this day the I Father Lord Byron was a poet and died when she was 8 years old accomplishments of those women are celebrated. I Mother Lady Wentworth was a social reformer I Descended from a wealthy family I Early interest in mathematics and science, encouraged by her mother Portrait I Obtained private classes and got in touch with intellectuals, e.g. Mary Sommerville who tutored her and later introduced Lovelace to Charles Babbage at the age of 17 I Married in 1835 William King at the age of 19, shortly after becoming the Countess of Lovelace I By 1839, she had given birth to 3 children I Continued studying maths, supported among others by Augustus De Morgan, a math professor in London who taught her via correspondence I In 1843, she published a translation of an Italian academic paper about Babbage's Analytical Engine and added her famous note section (see Contributions) I Died on November 27th, 1852 at the age of 36 Contributions I First computer programmer, roughly a century before the electronic computer I A two decade lasting correspondence with Babbage about his idea of an Analytical Engine I Developed an algorithm that would enable the Analytical Engine to calculate a sequence of Bernoulli numbers, unfortunately, the machine was never built I First person to realize the power of computer programs: Not only used for calculations with numbers I Combined arts and logic, calling it poetical science Figure 3:Ada Lovelace I First reflections about artificial intelligence, but she rejected the idea Bernoulli Numbers Quotes I Play an important role in several domains of mathematics, e.g.
    [Show full text]
  • Analytical Engine: the Orig- Inal Computer
    Chapter 2 Analytical Engine: The Orig- inal Computer As we learned in the fourth grade science course, back in 1801, a French man, Joseph Marie Jacquard, invented a power loom that could weave textiles, which had been done for a long time by hand. More interestingly, this machine can weave tex- tiles with patterns such as brocade, damask, and matelasse by controlling the operation with punched wooden cards, held together in a long row by rope. 1 How do these cards work? Each wooden card comes with punched holes, each row of which corresponds to one row of the design. In each position, if the needle needs to go through, there is a hole; other- wise, there is no hole. Multiple rows of holes are punched on each card and all the cards that compose the design of the textile are hooked together in order. 2 What do we get? With the control of such cards, needs go back and forth, moving from left to the right, row by row, and come up with something like the following: Although the punched card concept was based on some even earlier invention by Basile Bou- chon around 1725, “the Jacquard loom was the first machine to use punch cards to con- trol a sequence of operations”. Let’s check out a little demo as how Jacquard’s machine worked. 3 Why do we talk about a loom? With Jacquard loom, if you want to switch to a different pattern, you simply change the punched cards. By the same token, with a modern computer, if you want it to run a different application, you simply load it with a different program, which used to keep on a deck of paper based punched cards.
    [Show full text]
  • Ada and the First Computer
    Ada and the First Computer The collaboration between Ada, countess of Lovelace, and computer pioneer Charles Babbage resulted in a landmark publication that described how to program the world’s first computer by Eugene Eric Kim and Betty Alexandra Toole eople called Augusta Ada King’s father “mad and bad” for his wild ways, but he was better known as Lord Byron, the poet. Ada inherited her famous father’s P way with words and his zest for life. She was a beautiful, flirtatious woman who hobnobbed with England’s elite and who died at the youthful age of 36, the same age at which her father died. And like Byron, Ada is best known for something she wrote. In 1843 she published an influential set of notes that described Charles Babbage’s An- alytical Engine, the first automatic, general-purpose computing machine ever designed. Although the Analytical Engine was never built—largely because Babbage could not raise the funds for its construction—Ada’s notes included a program for using it to com- pute a series of figures called Bernoulli numbers [see box on page 78]. Ada’s notes established her importance in computer science, but her fascinating life and lineage—and her role as a female pioneer in a field in which women have always been notoriously underrepresented—have lately turned her into an icon. In addition to numerous biographies, she has inspired plays and novels written by the likes of such lu- minaries as Tom Stoppard and Arthur C. Clarke. Conceiving Ada, a movie loosely based on her life, was released by Fox Lorber in February.
    [Show full text]
  • A Short History of Computing
    A Short History of Computing 01/15/15 1 Jacques de Vaucanson 1709-1782 • Gifted French artist and inventor • Son of a glove-maker, aspired to be a clock- maker • 1727-1743 – Created a series of mechanical automations that simulated life. • Best remembered is the “Digesting Duck”, which had over 400 parts. • Also worked to automate looms, creating the first automated loom in 1745. 01/15/15 2 1805 - Jacquard Loom • First fully automated and programmable loom • Used punch cards to “program” the pattern to be woven into cloth 01/15/15 3 Charles Babbage 1791-1871 • English mathematician, engineer, philosopher and inventor. • Originated the concept of the programmable computer, and designed one. • Could also be a Jerk. 01/15/15 4 1822 – Difference Engine Numerical tables were constructed by hand using large numbers of human “computers” (one who computes). Annoyed by the many human errors this produced, Charles Babbage designed a “difference engine” that could calculate values of polynomial functions. It was never completed, although much work was done and money spent. Book Recommendation: The Difference Engine: Charles Babbage and the Quest to Build the First Computer by Doron Swade 01/15/15 5 1837 – Analytical Engine Charles Babbage first described a general purpose analytical engine in 1837, but worked on the design until his death in 1871. It was never built due to lack of manufacturing precision. As designed, it would have been programmed using punch-cards and would have included features such as sequential control, loops, conditionals and branching. If constructed, it would have been the first “computer” as we think of them today.
    [Show full text]
  • NVS 3-1-2 P-Jagoda
    Clacking Control Societies: Steampunk, History, and the Difference Engine of Escape Patrick Jagoda (University of Chicago, Illinois, USA) Abstract: Steampunk fiction uses strategic anachronism, counterfactual scenarios, and historical contingency in order to explore the interconnections between nineteenth-century and contemporary techno-scientific culture. William Gibson and Bruce Sterling’s novel The Difference Engine (1990), a prominent exemplar of this contemporary genre, depicts a neo- Victorian setting in which the inventor Charles Babbage builds a proto-computer based on the “Analytical Engine” design that he proposed but never actually constructed in our own nineteenth century. The alternative chronology of the novel re-imagines Victorian texts and historical events, including Benjamin Disraeli’s Sybil (1845) and the industrial revolution, in order to examine literary history and investigate historiography. This essay analyses The Difference Engine ’s commentary on the history of power relations. It contends that the novel’s alternative genealogy helps us examine the evolution of control systems and think about the shape of history. Keywords : biopolitics, control, The Difference Engine , William Gibson, historiography, power, self-reflexivity, steampunk, Bruce Sterling, technology. ***** Verily it was another world then…. Another world, truly: and this present poor distressed world might get some profit by looking wisely into it, instead of foolishly. (Thomas Carlyle, Past and Present [1843], 2009: 53-54) “But then Stephen does
    [Show full text]
  • Introduction to Computing: Explorations in Language, Logic, And
    6 Machines It is unworthy of excellent people to lose hours like slaves in the labor of calculation which could safely be relegated to anyone else if machines were used. Gottfried Wilhelm von Leibniz, 1685 The first five chapters focused on ways to use language to describe procedures. Although finding ways to describe procedures succinctly and precisely would be worthwhile even if we did not have machines to carry out those procedures, the tremendous practical value we gain from being able to describe procedures comes from the ability of computers to carry out those procedures astoundingly quickly, reliably, and inexpensively. As a very rough approximation, a typical laptop gives an individual computing power comparable to having every living human on the planet working for you without ever making a mistake or needing a break. This chapter introduces computing machines. Computers are different from other machines in two key ways: 1. Whereas other machines amplify or extend our physical abilities, comput- ers amplify and extend our mental abilities. 2. Whereas other machines are designed for a few specific tasks, computers can be programmed to perform many tasks. The simple computer model introduced in this chapter can perform all possible computations. The next section gives a brief history of computing machines, from prehistoric calculating aids to the design of the first universal computers. Section 6.2 ex- plains how machines can implement logic. Section 6.3 introduces a simple ab- stract model of a computing machine that is powerful enough to carry out any algorithm. We provide only a very shallow introduction to how machines can implement computations.
    [Show full text]
  • History of ENIAC
    A Short History of the Second American Revolution by Dilys Winegrad and Atsushi Akera (1) Today, the northeast corner of the old Moore School building at the University of Pennsylvania houses a bank of advanced computing workstations maintained by the professional staff of the Computing and Educational Technology Service of Penn's School of Engineering and Applied Science. There, fifty years ago, in a larger room with drab- colored walls and open rafters, stood the first general purpose electronic computer, the Electronic Numerical Integrator And Computer, or ENIAC. It spanned 150 feet in width with twenty banks of flashing lights indicating the results of its computations. ENIAC could add 5,000 numbers or do fourteen 10-digit multiplications in a second-- dead slow by present-day standards, but fast compared with the same task performed on a hand calculator. The fastest mechanical relay computers being operated experimentally at Harvard, Bell Laboratories, and elsewhere could do no more than 15 to 50 additions per second, a full two orders of magnitude slower. By showing that electronic computing circuitry could actually work, ENIAC paved the way for the modern computing industry that stands as its great legacy. ENIAC was by no means the first computer. In 1839, an Englishman Charles Babbage designed and developed the first true mechanical digital computer, which he described as a "difference engine," for solving mathematical problems including simple differential equations. He was assisted in his work by a woman mathematician, Ada Countess Lovelace, a member of the aristocracy and the daughter of Lord Byron. They worked out the mathematics of mechanical computation, which, in turn, led Babbage to design the more ambitious analytical engine.
    [Show full text]
  • Analytical Engine NEWSLETTER of the COMPUTER HISTORY ASSOCIATION of CALIFORNIA It's Been Almost More Than We Can Keep up Editorial: CAMPAIGN 1994 With
    January-~Iarch 1994 Volume 1.3 The Analytical Engine NEWSLETTER OF THE COMPUTER HISTORY ASSOCIATION OF CALIFORNIA it's been almost more than we can keep up Editorial: CAMPAIGN 1994 with. Now we need size. Size means weight; The Association begins a new year, and presence; recognition; visibility. Size convinces everything we had dreamed of doing, we're donors that charitable organizations are . doing. The ENGINE gets thicker, the e-mail worthy and credible. Size helps us reach out deeper. New computers - well, new old to potential members. Size brings down costs computers - are lugged to our doorstep. through economies of scale. Size will make Delivery vans bring boxes of books and files. the ENGINE a more attractive, more com­ Collaborations are proposed, exhibits planned, prehensive newsletter. names written excitedly on scraps of paper and then logged. And under it all the cer­ And size alone won't build a museum - but tainty, slightly awed still: This thing is it's a key ingredient in the dealing we'll need working. to do, between now and 1999. We promised to build, from the outset, an So we're calling our own bluff. By the end of organization with room to grow - an organi­ 1994, a year from this publication, we want zation that could start with a few like-minded 1,994 new members and ENGINE subscribers individuals, and smoothly become a major for the CHACo Promotions, perks, collabora­ voice for the preservation of computers and tions, colloquia, prizes, press releases, or their history, without spending scarce energy (even) a party - whatever it takes, we'll do.
    [Show full text]
  • The Multifaceted Impact of Ada Lovelace in the Digital Age
    Artificial Intelligence 235 (2016) 58–62 Contents lists available at ScienceDirect Artificial Intelligence www.elsevier.com/locate/artint The multifaceted impact of Ada Lovelace in the digital age Luigia Carlucci Aiello Department of Computer, Control, and Management Engineering Antonio Ruberti, Sapienza University of Rome, via Ariosto 25, 00185 Rome, Italy a r t i c l e i n f o a b s t r a c t Article history: Ada Lovelace (1815–1852), the Victorian-era mathematician daughter of the Romantic poet Received 23 February 2016 Lord Byron, is famous for her work with Charles Babbage on the Analytic Engine and is Accepted 25 February 2016 widely celebrated as the first computer programmer. Her work has been recognized over Available online 2 March 2016 the years, and even though the bearing of her contribution has often been questioned, she has always been acknowledged as a pioneering figure by the Computer Science community. Keywords: Recently she has been chosen as a symbol of the achievements of women in Science, Ada Byron Lovelace The first programmer Technology, Engineering and Mathematics (STEM). History of Computer Science Ada was worldwide celebrated on December 10th 2015, on the occasion of her 200th History of Artificial Intelligence birthday, with workshops, meetings, and publications. In particular, ACM contributed with a book: an interdisciplinary collection of papers inspired by Ada’s life, work, and legacy. The book covers Ada’s collaboration with Babbage, her position in the Victorian and steampunk literature, her representation in contemporary art and comics, and her increasing relevance in promoting women in science and technology.
    [Show full text]
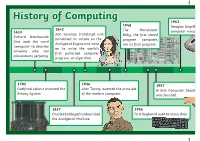
  • History of Computing 1963 a Search Engine Called Microsoft Was Founded
    1994 1975 History of Computing 1963 A search engine called Microsoft was founded. 1948 Douglas Engelbart invented the Yahoo was released. 2002 1842 The Manchester 2013 1613 computer mouse. Microsoft launched Ada Lovelace translated and Baby, the first stored Xbox One was released. Richard Braithwaite the tablet PC. annotated an article on the program computer, 1992 first used the word Analytical Engine and went ran its first program. The Internet was freed from ‘computer’ to describe 1971 2006 on to write the world’s government control. 2020 someone who did The first network email was sent The first tweet was sent first published computer Apple rumoured be to calculations perfectly. by Ray Tomlinson. to Twitter. program, or algorithm. releasing AirTags. 1986 1703 1936 1957 1972 The first PC virus was released. 2015 Gottfried Leibniz invented the Alan Turing invented the principle British Computer Society (BCS) Clive Sinclair produced the first 2001 The Apple Watch Binary System. of the modern computer. was founded. pocket calculator. Apple launched the iPod. was launched. 2016 1981 1997 Apple released First ‘portable’ computer was 1837 1956 An artificially intelligent AirPods. First keyboard used to input data. launched. It was the size of a Charles Babbage first described supercomputer beat the chess large suitcase. the Analytical Machine. champion Gary Kasporov. 2007 The iPhone was introduced. 1994 1975 History of Computing 1963 A search engine called Microsoft was founded. 1948 Douglas Engelbart invented the Yahoo was released. 2002 1842 The Manchester 2013 1613 computer mouse. Microsoft launched Ada Lovelace translated and Baby, the first stored Xbox One was released.
    [Show full text]
  • Analyticdb-V: a Hybrid Analytical Engine Towards Query Fusion for Structured and Unstructured Data
    AnalyticDB-V: A Hybrid Analytical Engine Towards Query Fusion for Structured and Unstructured Data Chuangxian Wei, Bin Wu, Sheng Wang, Renjie Lou, Chaoqun Zhan, Feifei Li, Yuanzhe Cai Alibaba Group fchuangxian.wcx,binwu.wb,sh.wang,json.lrj,lizhe.zcq,lifeifei,yuanzhe.cyzg @alibaba-inc.com ABSTRACT apps. For example, during the 2019 Singles' Day Global With the explosive growth of unstructured data (such as Shopping Festival, up to 500PB unstructured data are in- images, videos, and audios), unstructured data analytics is gested into the core storage system at Alibaba. To facilitate widespread in a rich vein of real-world applications. Many analytics on unstructured data, content-based retrieval sys- database systems start to incorporate unstructured data tems [45] are usually leveraged. In these systems, each piece analysis to meet such demands. However, queries over un- of unstructured data (e.g., an image) is first converted into structured and structured data are often treated as disjoint a high dimensional feature vector, and subsequent retrievals tasks in most systems, where hybrid queries (i.e., involving are conducted on these vectors. Such vector retrievals are both data types) are not yet fully supported. widespread in various domains, such as face recognition [47, In this paper, we present a hybrid analytic engine devel- 18], person/vehicle re-identification [56, 32], recommenda- oped at Alibaba, named AnalyticDB-V (ADBV), to fulfill tion [49], and voiceprint recognition [42]. At Alibaba, we such emerging demands. ADBV offers an interface that en- also adopt this approach in our production systems. ables users to express hybrid queries using SQL semantics Although content-based retrieval system supports unstruc- by converting unstructured data to high dimensional vec- tured data analytics, there are many scenarios where both tors.
    [Show full text]