DOCSLIB.ORG

Chapter Fifteen Ac Drives

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chapter Fifteen Ac Drives Power Electronics and Drives CHAPTER FIFTEEN AC DRIVES 15.1 INTRODUCTION AC drives is a term used to refer to equipment designed to control the speed of an a.c. motor. They receive a.c. power and convert it to an adjustable frequency, adjustable voltage output for controlling motor operation. Inverters and other types of frequency changers are typical examples of modern a.c. drives which are also called adjustable frequency drives. A typical inverter receives 400 V a.c., three-phase, 50 Hz input power and in turn provides the proper voltage and frequency for a given speed to the motor. The three common inverter types are the variable voltage inverter (VVI), current source inverter (CSI), and pulse width modulation (PWM). Another type of a.c. drive is a cycloconverter. These are commonly used for very large motors used in steel industry and mils. The cycloconverters is an arrangement of poly-phase rectifiers in which the firing delay is cyclically varied to synthesise an a.c. output, instead of the set delay for producing a controllable d.c. for the d.c. motor previously mentioned. A feature of a.c. drives is the ability to increase or decrease the voltage and frequency to a motor gradually. This accelerates the motor smoothly with less stress on the motor and connected load. Smoothing is a feature that can be added to the acceleration/ deceleration operation. This feature smoothes the transition between starting and steady-state operation. There are several types of a.c. motors used in industrial applications that need real drives to suit a given task. In all types of drives, motors and load have stored energy which can be either regenerated or dissipated as the load speed falls. One third of the world's electricity consumption is used for running induction motors driving pumps, fans, compressors, elevators and machinery of various types. In general, the speed of a.c. motors depends on the frequency of the supply voltage and the number of magnetic poles per phase in the stator. Early speed controllers depended 649 Power Electronics and Drives on switching in different numbers of poles and control was only available manually and in crude steps. Modern electronic drives make continuously variable frequency supplies possible permitting closed-loop speed control. This chapter is intended to provide a basic understanding of a.c. drive terms, types and theory of operations. Benefits of AC drive Large energy savings at lower speed. Increased life of rotating components due to lower operating speed. Reduced noise and vibration level. Reduction of thermal and mechanical stresses. Lower kVA. High power factor. 15.2 TYPES OF AC MOTORS The types of a.c. motor available in industry are classified according to the supply as single-phase and poly-phase motors. These two types may also be classified according to the principle of operation into induction type and synchronous type as follows: 1- single-phase motors (a) Induction type-squirrel cage (i) Split-phase (ii) Capacitor start (iii) Permanent split capacitor (iv) Capacitor start / capacitor run (v) Split-phase start / capacitor run (vi) Shaded pole (b) Induction type-wound rotor (i) Repulsion (ii) Repulsion start (iii) Repulsion induction (c) Single-phase synchronous (i) Hysteresis (ii) Reluctance (iii) Permanent magnet (d) Single-phase universal motor (AC and DC) 2- Poly-phase motors (a) Induction type (i) Wound rotor (ii) Squirrel – cage (b) Synchronous 656 Power Electronics and Drives These motors are summarised in the following diagram (Fig.15.1) , Split –phase Capacitor start Squirrel Permanent capacitor -cage Capacitor start capacitor run Shaded -pole Single-phase Induction Wound Repulsion Universal rotor Repulsion start Repulsion induction AC and DC Synchronous Hysteresis AC Reluctance Motors Permanent magnet Induction Wound rotor Poly-phase Synchronous Squirrel -cage Fig.15.1 Types of a.c. motors. 15.3 THREE-PHASE INDUCTION MOTOR : REVISION OF EQUATIONS The three-phase induction motors ( also called asynchronous motors) are the most widely used electric motors in industry. The popularity of this type of motors in most industrial applications is because of their simple, robust construction because they can build without slip-rings or commutator, rugged, relatively cheap, require little maintenance and have self-starting torque. An induction motor of a medium size may have an efficiency as high as 90 percent and power factor of nearly 0.9. The physical size of such a motor for a given output rating is small as compared with d.c. and a.c. synchronous motors of same rating. There is another distinguishing feature of induction motor is that it is a singly excited machine, i.e. only the stator winding is connected to the a.c. supply, no electrical connection from the supply to the rotor is needed. Finally It can be manufactured with characteristics to suit most industrial requirements. 656 Power Electronics and Drives Beside the above numerous advantages of the induction motor, it has two main inherent disadvantages: 1. Its starting torque is inferior to d.c. shunt motor. 2. It is essentially a constant speed motor and its speed cannot be changed easily. The speed of an induction motor is determined by the supply frequ- ency and number of poles, with a few percent regulation from no-load to full-load. However, the speed is frequency dependent and consequently these motors are not easily adapted to speed control. A wide range of speed control is only possible by using expensive power electronic circuit with advanced digital control. We usually prefer d.c. motors when large speed variations are required due to its inexpensive methods of control. 15.3.1 Basic Principles of Three-Phase Induction Motor with Sinusoidal Supply Voltages Like any electric motor, a three-phase induction motor has a stator and a rotor. The stator carries a three-phase winding (called stator winding) while the rotor carries a short-circuited winding (called rotor winding). Only the stator winding is fed from three-phase supply. The rotor winding derives its voltage and power from the externally energized stator winding through electromagnetic induction and hence such a machine is often called the induction machine. The induction motor may be considered to be a transformer with a rotating secondary in the sense that the power is transferred from the stator (primary) to the rotor (secondary) winding only by mutual induction. Hence, it can, therefore, be described as a “transformer type” a.c. machine in which electrical energy is converted into mechanical energy. When the stator windings are connected to a set of balanced three- phase voltages and the rotor circuit is closed, the resulting three-phase current establish a rotating mmf wave that results in a flux wave of constant amplitude rotating at constant speed known as the synchronous speed. The value of the synchronous speed is fixed by two parameters: (a)The supply frequency, (Hertz), (b)The number of poles p for which the primary is wound. The synchronous speed of the rotating magnetic field is given by The number of poles p must be an even integer since for every north pole there is a corresponding south pole. The following Table-15.1 shows motors speeds for motors with different numbers of poles working with different a.c. supply frequencies. 656 Power Electronics and Drives Table 15.1. Synchronous speed of induction motor for different number of poles. Rotor Speed (rpm) Number of 2 4 6 8 10 12 poles (p) Frequency 3000 1500 1000 750 600 500 f = 50 Hz Frequency 3600 1800 1200 900 720 600 f = 60 Hz An induction motor runs at a shaft speed n that is less than the synchr- onous speed at which the stator rotating field is rotate. The speed difference is called the slip speed. The ratio of slip speed to synchronous speed is the most important variable in induction motor operation and is called the per-unit slip s, and is given by: where s is the slip in per unit, ns is the synchronous speed in rpm, and n is the rotor speed. Since the rotor current is proportional to the relative motion between the rotating field and the rotor speed, the rotor current and hence the torque are both directly proportional to the slip. For particular cases, the slip of the motor will have the following special values: When the motor is running at synchronous speed , i.e. and . At standstill and . If the motor is rotating at synchronous speed in the reverse direction, then and . Squirrel cage motors are built with the slip ranging from about 3 – 20%. Motors with a slip of 5% or higher are used for hard-to-start applications. A motor with a slip of 5% or less is called a normal slip motor. A normal slip motor is often referred to as a constant speed motor because the speed changes very little with variations in load. At full load the per-unit slip usually 5% for a small motor because . 656 Power Electronics and Drives 15.3.2 Development of Circuit Model (Equivalent Circuit) Standstill Operation At standstill, the motor can be considered as a static transformer with primary (stator) winding and secondary (rotor) winding. If the stator is fed from a three-phase supply with voltage V1 is the phase voltage, the air gap field produced rotates at synchronous speed ns . This field induces emfs E1 and E2 in both the stator and rotor winding respectively. The magnitudes of these emfs are given by, assuming unity winding factor (kw =1) , where is the effective transformation (turns) ratio between the stator and rotor winding which is usually greater than unity and is typically in the range 1.1 – 1.3.
Load more

Recommended publications
  • Lci's and Synchronous Motors Applied to Roller Mills
    LCI'S AND SYNCHRONOUS MOTORS APPLIED TO ROLLER MILLS For Presentation at the IEEEIPCA Cement Industry Technical Conference Salt Lake City, UT May 2000 By: James F. Zayechek G E Industrial Systems 1. Abstract A cement company concerned about high power-factor penalty costs requested an evaluation of the feasibility of using synchronous motors starting through LCl's to drive three new roller mills at a cement plant. The prior experience with roller mills centered about the application of wound rotor induction motors with either cascaded secondary resistance or liquid rheostat. By utilizing synchronous motors, there was the possibility of providing leading power factor to reduce the reactive power demands seen by the utility feeding the cement plant. It was theorized that, if sufficient power factor correction could be obtained, the payback period of the incremental additional cost of the synchronous motor drive system would be very short. After payback of the initial investment, all future energy savings gravitate directly to the bottom line as additional revenue. Several key concerns had to be addressed in evaluating the use of synchronous motors for these relatively high starting torque requirement applications. This paper discusses the electrical and mechanical evaluation leading up to the decision to proceed with this new application of synchronous motors started through an LCI. 2. Introduction Roller mills, also known as vertical mills, are becoming more prevalent in modern cement plants. These mills have application both for raw material preparation and clinker grinding to final specifications. The increasingly competitive nature of today's business environment is pushing the mill OEM's to larger mills with greater throughput.
    [Show full text]
  • Power Processing, Part 1. Electric Machinery Analysis
    DOCONEIT MORE BD 179 391 SE 029 295,. a 'AUTHOR Hamilton, Howard B. :TITLE Power Processing, Part 1.Electic Machinery Analyiis. ) INSTITUTION Pittsburgh Onii., Pa. SPONS AGENCY National Science Foundation, Washingtcn, PUB DATE 70 GRANT NSF-GY-4138 NOTE 4913.; For related documents, see SE 029 296-298 n EDRS PRICE MF01/PC10 PusiPostage. DESCRIPTORS *College Science; Ciirriculum Develoiment; ElectricityrFlectrOmechanical lechnology: Electronics; *Fagineering.Education; Higher Education;,Instructional'Materials; *Science Courses; Science Curiiculum:.*Science Education; *Science Materials; SCientific Concepts ABSTRACT A This publication was developed as aportion of a two-semester sequence commeicing ateither the sixth cr'seventh term of,the undergraduate program inelectrical engineering at the University of Pittsburgh. The materials of thetwo courses, produced by a ional Science Foundation grant, are concernedwith power convrs systems comprising power electronicdevices, electrouthchanical energy converters, and associated,logic Configurations necessary to cause the system to behave in a prescribed fashion. The emphisis in this portionof the two course sequence (Part 1)is on electric machinery analysis. lechnigues app;icable'to electric machines under dynamicconditions are anallzed. This publication consists of sevenchapters which cW-al with: (1) basic principles: (2) elementary concept of torqueand geherated voltage; (3)tile generalized machine;(4i direct current (7) macrimes; (5) cross field machines;(6),synchronous machines; and polyphase
    [Show full text]
  • Dynamic Suspension Modeling of an Eddy-Current Device: an Application to Maglev
    DYNAMIC SUSPENSION MODELING OF AN EDDY-CURRENT DEVICE: AN APPLICATION TO MAGLEV by Nirmal Paudel A dissertation submitted to the faculty of The University of North Carolina at Charlotte in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Electrical Engineering Charlotte 2012 Approved by: Dr. Jonathan Z. Bird Dr. Yogendra P. Kakad Dr. Robert W. Cox Dr. Scott D. Kelly ii c 2012 Nirmal Paudel ALL RIGHTS RESERVED iii ABSTRACT NIRMAL PAUDEL. Dynamic suspension modeling of an eddy-current device: an application to Maglev. (Under the direction of DR. JONATHAN Z. BIRD) When a magnetic source is simultaneously oscillated and translationally moved above a linear conductive passive guideway such as aluminum, eddy-currents are in- duced that give rise to a time-varying opposing field in the air-gap. This time-varying opposing field interacts with the source field, creating simultaneously suspension, propulsion or braking and lateral forces that are required for a Maglev system. In this thesis, a two-dimensional (2-D) analytic based steady-state eddy-current model has been derived for the case when an arbitrary magnetic source is oscillated and moved in two directions above a conductive guideway using a spatial Fourier transform technique. The problem is formulated using both the magnetic vector potential, A, and scalar potential, φ. Using this novel A-φ approach the magnetic source needs to be incorporated only into the boundary conditions of the guideway and only the magnitude of the source field along the guideway surface is required in order to compute the forces and power loss.
    [Show full text]
  • POWER ELECTRONICS TRAINER (Model : XPO-PE) / MICROCONTROLLER BASED PE (Model : XPO-Μc LSPT)
    POWER ELECTRONICS TRAINER (Model : XPO-PE) / MICROCONTROLLER BASED PE (Model : XPO-µC LSPT) SALIENT FEATURES u Aesthetically designed injection molded electronic desk. u Master unit carrying useful experiment resources like line Synchronized firing circuits, Power supplies, lamp load, RLC loads, Battery charging supply etc. while the central slot will hold replaceable experiment panels. u Each multi experiment panel is secured in an ABS molded plastic sturdy enclosure, and has colorful screw less overlay showing circuit & Connection through Sturdy 4mm Banana Sockets & Patch Chords. u Set of User Guide provided with each unit. u Order 6 Master units and set of 6 panels (PE 1 x 2 , PE2, PE3, PE6X2nos)+ Power scope, buy more of PE1 and PE6 being major panels. Master Unit Accessories: Built in power supply l 15 pin D connector cable assembly, u DC supply : + 12V, 500mA, l 4mm patchcords : 100mm X 10 Nos & 500mm X 20 Nos. u Unregulated Power supply 17V / 750mA, Optional Power Scope u Regulated 7VDC to 14VDC/3A O/P is provided as 12V Battery charging supply. In absence of battery, same may be used as simulated battery source to run experiments on inverters etc. u Isolated DC supply +12V/ 300mA with isolated common. u On board Inverter transformer of Primary & Secondaries: 12-11-0- 11-12/3A. u On board o/p to Isolated Drive Circuit AC supply u 230V AC line voltage is made available on two banana 4mm Accessory for any Lab CRO for off ground differential measurements sockets as well as 1.5A fuse extender for variac if used.
    [Show full text]
  • A Survey of Propulsion Systems for High Capacity Personal Rapid Transit
    T NO UMTA-MA-06-0 04 8-75-2 A SURVEY OF PROPULSION SYSTEMS FOR HIGH CAPACITY PERSONAL RAPID TRANSIT Thorleif Knutrud JULY 1975 FINAL REPORT DOCUMENT IS AVAILABLE TO THE PUBLIC THROUGH THE NATIONAL TECHNICAL INFORMATION SERVICE, SPRINGFIELD VIRGINIA 22161 Prepared for u.s. DEPARTMENT OF TRANSPORTATION URBAN MASS TRANSPORTATION ADMINISTRATION Office of Research and Development Washington DC 20590 . NOTICE This document is disseminated under the sponsorship of the Department of Transportation in the interest of information exchange. The United States Govern- ment assumes no liability for its contents or use thereof NOTICE The United States Government does not endorse products or manufacturers. Trade or manufacturers' names appear herein solely because they are con- sidered essential to the object of this report. 7 , Htr . /V3 a/c? “DOT - Tsc- u. ~7&~ /£“ TECHNICAL REPORT STANDARD TITLE RAGE 3. Recipient's Catalog No. 1 . Report No. 2. Government Accesnon No. UMTA-MA- 0 6- 0 048-75-2 5. Report Date 4. T i tie and Subtitle July 1975 A SURVEY OF PROPULSION SYSTEMS FOR 6. Performing Organization Code HIGH CAPACITY PERSONAL RAPID TRANSIT 7. Author's) 8. Peefarming Orgonrzatron Report No Thorleif Knutrud DOT -TSC -UMTA-7 5-15 9. Performing Organization Name and Address 10. Work Unit No UM533/R6751 Alexander Kusko, * Inc.* 11. Controct or Grant No 161 Highland Avenue DOT -TSC- 2 03/DOT- TSC- 965 Needham Heights MA 02194 15. 13. Type of Report and Period Covered 12. Sponsoring Agency Nome ond Address Final Report U.S. Department of Transportation July 1974 - June 1975 16.Urban Mass Transportation Administration Office of Research and Development 14.
    [Show full text]
  • Universal Motor - Construction, Working and Characteristics
    Universal Motor - construction, working and characteristics. A universal motor is a special type of motor which is designed to run on either DC or single phase AC supply. These motors are generally series wound (armature and field winding are in series), and hence produce high starting torque (See characteristics of DC motors here). That is why, universal motors generally comes built into the device they are meant to drive. Most of the universal motors are designed to operate at higher speeds, exceeding 3500 RPM. They run at lower speed on AC supply than they run on DC supply of same voltage, due to the reactance voltage drop which is present in AC and not in DC. There are two basic types of universal motor : (i)compensated type and (ii) uncompensated type. Construction of Universal motor Construction of a universal motor is very similar to the construction of a DC machine. It consists of a stator on which field poles are mounted. Field coils are wound on the field poles. However, the whole magnetic path (stator field circuit and also armature) is laminated. Lamination is necessary to minimize the eddy currents which induce while operating on AC. The rotary armature is of wound type having straight or skewed slots and commutator with brushes resting on it. The commutation on AC is poorer than that for DC. because of the current induced in the armature coils. For that reason brushes used are having high resistance. Working of universal motor A universal motor works on either DC or single phase AC supply. When the universal motor is fed with a DC supply, it works as a DC series motor.
    [Show full text]
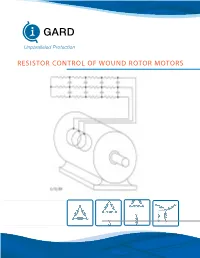
  • Resistor Control of Wound Rotor Motors Resistor Control of Wound Rotor Motors
    RESISTOR CONTROL OF WOUND ROTOR MOTORS RESISTOR CONTROL OF WOUND ROTOR MOTORS The Wound Rotor Induction Motor or Slip Ring Motor is widely used for applications requiring speed control or low starting currents. It is very similar to the Squirrel Cage Induction Motor except that the rotor leads are brought out through slip rings (commutator rings) so that external resistance may be inserted. In fact, if we shorted these three rotor leads together, we would basically have a squirrel cage motor. The beauty of the WRM is that we can control the torque of the motor with external resistors. The purpose of this paper is to show how these resistors are sized and connected for simple speed control or starting duty. STATIR CIRCUIT The Stator, or stationary winding, of the WRM is a three-phase winding which has a cylindrical shape and occupies the outer part of the motor just inside of the motor frame. The three primary leads are usually connected (through a contactor) to the 460 VAC 3ph, 60hz power lines. The three- phase power, applied to the stator windings, produces a rotating magnetic field. The mathematics are complex and will not be covered here. The main thing to remember is that a constantly rotating magnetic field is produced whenever the stator is energized. The speed or RPM of this rotating magnetic field is a function of how many “poles” are created by the windings and the frequency of the incoming power (60 cycles per second in this country, 50 cycles per second in many European countries). With 60hz power, this synchronous RPM is a multiple of 60 such as 360, 900, 1800, etc.
    [Show full text]
  • ADJUSTABLE SPEED DRIVES By: Richard D
    Service Application Manual SAM Chapter 620-130 Section 6A ADJUSTABLE SPEED DRIVES By: Richard D. Beard P.E. Consultant, RSES Manufacturers’ Service Advisory Council INTRODUCTION Many commercial and industrial machines and processes require adjustable speed. Adjustable speed usually makes a machine more universally compatible and increases its versatility. Adjustable-speed drives also are being used in residential equipment, including air conditioners, refrigerators, heat pumps, furnaces, and other devices driven by motors. These drives optimize speed and torque, making them generally more efficient than non-adjustable-speed drives. An adjustable-speed motor is one in which the speed can be varied gradually over a wide range—but, once adjusted, it remains nearly unaffected by the load. A variable-speed motor is one in which the speed varies with the load, usually decreasing when the load increases. The term "adjustable speed" implies that some external adjustment, which is independent of load, will cause the speed to change. A variable-frequency inverter drive is an example. The term "variable speed" describes a drive in which load changes inherently cause significant changes in speed. A direct current series motor, for example, exhibits this characteristic. An adjustable variable-speed motor is one in which the speed can be adjusted gradually. However, once adjusted for a given load, the speed will vary with changes in the load. A multispeed motor is one that can be operated at any one of two or more definite speeds, each being practically independent of the load. The multispeed motor is neither an adjustable-speed nor a variable-speed drive. Multispeed motors usually have two, three, or four definite operating speeds.
    [Show full text]
  • UNIVERSAL MOTORS Universal Motor
    UNIVERSAL MOTORS Universal motor The motors which can be used with a single phase AC source as well as a DC source of supply and voltages are called as Universal Motor. It is also known as Single Phase Series Motor. A universal motor is a commutation type motor. Construction of the universal motor The construction of the universal motor is same as that of the series motor. I n o rd e r t o m i n i m i z e t h e p ro b l e m o f commutation, high resistance brushes with increased brush area are used. To reduce Eddy current losses the stator core and yoke are laminated. The Universal motor is simple and less costly. It is used usually for rating not greater than 7 5 0 W . Characteristic of Universal motor The characteristic of Universal motor is similar to that of the DC series motor. When operating from an AC supply, the series motor develops less torque. By interchanging connections of the fields with respect to the armature, the direction of rotation can be altered. Universal motor T h e d i r e c t i o n o f t h e developed torque will re m a i n p o s i t i v e , a n d direction of the rotation will be as it was before. The nature of the torque will be pulsating, and the frequency will be twice that of line frequency as shown in the waveform. Universal motor Thus, a Universal motor can work on both AC and DC.
    [Show full text]
  • Design and Simulation of Leakage Current in Smart Power Module (Spm) Motor Drive Application
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by UTHM Institutional Repository DESIGN AND SIMULATION OF LEAKAGE CURRENT IN SMART POWER MODULE (SPM) MOTOR DRIVE APPLICATION SYAHFITRI BIN SAIDIN A project report submitted in partial fulfillment of the requirement for the award of the Degree of Master of Electrical Engineering Faculty Of Electrical And Electronics Engineering Universiti Tun Hussein Onn Malaysia DECEMBER 2013 vi CONTENTS TITLE i DECLARATION ii DEDICATION iii ACKNOWLEDGEMENT iv ABSTRACT v CONTENTS vi LIST OF FIGURES x LIST OF TABLES xiv LIST OF SYMBOL AND ABBREAVIATION xv LIST OF APPENDIXES xvi CHAPTER 1 INTRODUCTION 1.1 General Background of Electric Motor 1 1.2 Universal Motor 3 1.2.1 Properties of Universal Motor 4 1.2.2 Applications of Universal Motor 6 1.3 DC Motor 7 1.3.1 Brush DC Motor 8 1.3.2 Brushless DC Motor 9 1.3.3 Permanent Magnet Stators 9 1.4 Smart Power Module (SPM) 10 1.5 Problem Statement 12 vii 1.6 Objectives and Scopes 1.6.1 Objective 13 1.6.2 Scope of Work 14 1.6.3 Thesis Overview 14 CHAPTER 2 LITERATURE REVIEW 2.1 Introduction 16 2.2 What Is Leakage Current? 16 2.2.1 Why Is It Important? 17 2.2.2 What Causes Leakage Current? 17 2.2.3 What Is A Safe Level 18 2.3 Direct Current Motor (Dc Motor) 19 2.3.1 Principle Of Dc Motor 19 2.3.2 Detailed Description Of A Dc Motor 21 2.3.3 Working Or Operating Principle Of Dc Motor 23 2.3.4 Construction Of Dc Motor 28 2.3.5 Permanent Magnet Stators 29 2.3.6 Electrical Connections Between The Stator And Rotor 30 2.4 Electricity Consumption By Electrical Motor Systems 31 2.5 Motor Efficiency 33 2.6 Brushless DC Motors (BLDC) 35 2.6.1 Brushless Vs.
    [Show full text]
  • Design Approach to a Wound Rotor Induction Motor Towards Optimization
    ISSN (Online) : 2454 -7190 ISSN (Print) 0973-8975 J.Mech.Cont.& Math. Sci., Vol.-13, No.-3, July-August (2018) Pages 159-172 Design approach to a wound rotor induction motor towards optimization 1Pritish Kumar Ghosh, 2Pradip Kumar Sadhu, 3Amarnath Sanyal, *4DebabrataRoy, 5Biswajit Dutta 1,2Electrical Engineering, Indian Institute of Technology (Indian School of Mines), Dhanbad, 826004, India 3Ex Power Engineering, Jadavpur University, Kolkata,W.B.- 700032,India 4Electrical Engineering,Techno International Batanagar, South 24Parganas, W.B.- 700141,India 5ElectricalEngineering,Seacom Engineering College,Howrah,W.B.-711302,India [email protected],[email protected],3ansanyal@yahoo. co.in,[email protected],[email protected], *Corresponding author: Debabrata Roy, Abstract About 88% of the driving power is produced by 3-phase and single-phase induction motors. In most part it is by squirrel-cage motors, only a small fraction by the slip-ring or phase-wound type. It is because the cage-type motors are relatively inexpensive. But they suffer from low p.f. operation and low starting torque which cannot be manipulated by inserting resistance in the rotor circuit. Also, this type of induction motors is not easily speed-adjustable. Though a little more expensive, the slip-ring type induction motors do not have these disadvantages. Therefore, they are used as speed-adjustable drives and for drives where heavy duty starting is involved. The design of any kind of power equipment should be made cost-optimally in the present day competitive market. A new approach to reaching optimal solution has been shown in this paper by the method of sequential searching with respect to the chosen design variables.
    [Show full text]
  • Dissectible Motors
    Dissectible Motors Educational Training Equipment for the 21st Century Bulletin 258E HDI-100 Dissectible Motors Purpose Hampden Dissectible Motors, Series HDI-100, are a versatile aid in teaching the construction, principle of operation, and operating character- istics of fractional horsepower motors. As such they complement and extend the Hampden Series 100 Rotating Electrical Machines Program. Description The four stators and corresponding rotors of Hampden’s Dissectible Motors are the same ones used in standard industrial motors. This provides the student with realistic construction and operating characteristics. Commutator, brushes, centrifugal switch, etc., may all be observed during operation. Each motor assembles in minutes. First the student clamps the selected stator on the ter- Single-phase motor assembled on standard mounting base. Note protective clear plastic cover. minal panel/base. Next, the rotor is inserted Shipping Weight: 125 lbs. and held in position by specially designed end bells. A coupling flange is then secured to the motor shaft. The student then chooses the ter- minal panel overlay for that motor and begins the experimentation. Hampden Dissectible Motors are furnished complete with cords. The motor program includes the following four motors: 1. DC Motor. This is a four-pole machine which may be operated as a shunt, or com- pound motor. Hampden Dissectible Motors include DC and Single-phase and Three-phase AC in fractional horsepower size. 2. Single-Phase AC Squirrel-Cage Induction Motor. This is a four-pole machine, rated at 1725 rpm, which operates on 115 or 230 MODEL WRM-100-HDI volts. Dissectible Wound Rotor Motor 3. Three-Phase, Four-Pole Squirrel-Cage Induction Motor.
    [Show full text]