DOCSLIB.ORG

Remote Sensing Math

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Remote Sensing Math National Aeronautics and Space Administration andSpace Aeronautics National R emot e S ensing M a th I Remote Sensing Remote sending of a dust devil on the surface of mars - NASA/Mars Rover/JPL A Brief Mathematical Guide Dr. Sten Odenwald NASA Space Math http://spacemath.gsfc.nasa.gov II This collection of activities is based on a weekly series of space science problems distributed to thousands of teachers during the 2009-2010 school year. They were intended for students looking for additional challenges in the math and physical science curriculum in grades 9 through 12. The problems were created to be authentic glimpses of modern science and engineering issues, often involving actual research data. The problems were designed to be ‘one-pagers’ with a Teacher’s Guide and Answer Key as a second page. This compact form was deemed very popular by participating teachers. Acknowledgments: We would like to thank Dr. Michael Wilson (University of Maryland) for his careful reading of the draft of this book, his extensive and efficient error-detection algorithm, and the many constructive comments made about problem content and level of difficulty. Dr. Wilson is a research associate for the Goddard Earth Sciences and Technology Center at the University of Maryland, Baltimore County. Mike received his Ph.D. in 2009 in Atmospheric Sciences from the University of Illinois at Urbana-Champaign, with a focus on remote sensing in the polar regions. His current work focuses on cloud radiative modeling and cloud detection in Landsat imagery. We would also like to thank Ms. Jeannette Allen and Anita Davis (NASA Goddard Eath Sciences Division) for their enthusiastic support of this resource and many helpful comments and suggestions. For more weekly classroom activities about astronomy and space visit the NASA website, http://spacemath.gsfc.nasa.gov To suggest math problem or science topic ideas, contact the Author, Dr. Sten Odenwald at [email protected] Front and back cover credits: Front: Collage (USGS); Earth globe (MODIS); Messier 82 (Spitzer/Hubble); Sun(SOHO/EIT) Back: Oman (Landsat); Mykolaiv Ukraine(Landsat) Interior: Mars Dust Devil (NASA/JPL) Space Math http://spacemath.gsfc.nasa.gov Table of Contents III Grade Page Acknowledgments ii Table of Contents iii Alignment with Standards vi Mathematics Topic Matrix vii How to use this Book xi Teacher Comments xii Introduction to Remote Sensing xiii 1.0 Digital Picture Basics Image Formats : Taking a digital picture 6-8 1 Counting Photons : Pixel math 6-8 2 Storing Pixel Data 6-8 3 Images as Arrays of Numbers 6-8 4 Image Math - Hot Pixels 6-8 5 Image Math - Dark Current 9-12 6 Image Math - Flat Fielding 9-12 7 Image Math – Manipulating arrays of numbers 9-12 8 Telemetry – Transmitting data back to Earth 9-12 9 Telemetry and Binary Numbers 6-8 10 Interplanetary Communication 9-12 11 Computer Memory and Glitches 9-12 12 Correcting Bad Data Using Parity Bits 6-8 13 Data Corruption by High Energy Particles 6-8 14 Working with Giga, Tera, Peta and Exa 6-8 15 2.0 Photons and Digital Imaging Digital Imaging - Working with Irradiance 9-12 16 Photons and Photon Energy 9-12 17 Camera Sensitivity and F-Stops 9-12 18 Sampling Error and Photon Statistics 9-12 19 Photon Statistics and Exposure 9-12 20 Photon Statistics and Brightness 9-12 21 3.0 Digital Calibration and Photometry Measuring Brightness – Photometry 9-12 22 Calibrating Data 9-12 23 Calibrating Scientific Images 9-12 24 Light Intensity and Pixel Data and DNs 9-12 25 Your Digital Camera – Image Processing 6-8 26 Your Digital Camera – Standard Sources of Intensity 9-12 27 Your Digital Camera – Converting DNs to Intensity units 9-12 28 Space Math http://spacemath.gsfc.nasa.gov Table of Contents (cont'd) IV Grade Page 4.0 Angular Resolution Angular Measure in Astronomy 6-8 29 Angular Size and Similar Triangles 6-8 30 Geometry and Angular Size 9-12 31 Resolving the Moon 9-12 32 Getting an Angle on the Sun and Moon 9-12 33 Angular Size: The Moon and Stars 9-12 34 SDO - Reveals Details on the Surface of the Sun 6-8 35 LRO - Spots a Rolling Lunar Bolder with no Moss! 6-8 36 LRO - A Detailed Study of the Apollo-11 Landing Area 6-8 37 LRO - Mare Nubium and Las Vegas 6-8 38 LRO - Explores Lunar Surface Cratering 6-8 39 Landsat – Exploring Washington DC 6-8 40 Landsat – Glacier Retreat 6-8 41 Landsat – Exploring Biomass Loss from a Large Fire 6-8 42 Hubble - The Changing Atmosphere of Pluto 9-12 43 Image Blurring and Motion 6-8 44 Angular Resolution and Wavelength 9-12 45 The Most Important Equation in Astronomy 6-8 46 Hinode – Closeup of a Sunspot 6-8 47 Ranger 9 – Craters are a Blast! 9-12 48 Chandra – The Hand of Chandra 6-8 49 Hubble – The Eagle Nebula Closeup 6-8 50 A High Resolution Satellite Photo 6-8 51 5.0 Multi-Wavelength Spatial Imaging Digital Imaging and Filters 9-12 52 Advanced Filter Math using Calculus 9-12 53 Identifying Materials by their Reflectivity 6-8 54 Reflectivity Fingerprints 6-8 55 Creating and Interpreting Images 6-8 56 Graphical Reflectivity Measurements 6-8 57 MMM - A Mineral Study of Mare Orientale 6-8 58 Understanding Mineral Reflectivity Spectra 6-8 59 IRTF-Asteroids and Ice 9-12 60 MMM-Water on the Moon 9-12 61 Terra - Earth’s Carbon Metabolism Revealed 9-12 62 Hinode - Seeing the Sun at X-ray wavelengths 6-8 63 Seeing the Sun at Radio Wavelengths 6-8 64 Terra – Carbon Monoxide a Deadly Trace Gas 9-12 65 SeaWifs – Studying Ocean Plankton from Space 9-12 66 Space Math http://spacemath.gsfc.nasa.gov Table of Contents (cont’d) V 6.0 Temporal Studies SDO - Measuring the Speed of an Eruptive Prominence 6-8 67 STEREO - Watching the Sun Kick Up a Storm 9-12 68 Chandra - Studying an Expanding Supernova Shell 6-8 69 Hubble - Tracking the Motion of an Asteroid 6-8 70 Hinode - Moving Magnetic Filaments Near Sunspots 9-12 71 Measuring the Speed of a Solar Tsunami 9-12 72 RHESSI - Super-fast Solar Flares 9-12 73 STEREO – The Comet Encke Tail Disruption Event 6-8 74 Hinode – How fast does the sun rotate? 6-8 75 Angular Size and Velocity 6-8 76 The Rate of Oil Leakage in the Gulf Oil Spill of 2010 9-12 77 Mars Rover – The Martian Dust Devils 6-8 78 7.0 Remote Sensing From Around the Cosmos GRACE – Exploring Earth’s Gravity Field 9-12 79 CHAMP- Magnetic Earth and Lithosphere 9-12 80 2MASS – How many stars are there? 6-8 81 IMAGE-The North and South Magnetic Poles 6-8 82 MARIA-Having a Hot Time on Mars 9-12 83 Deep Impact - Tempel-1 Close up of a Comet 6-8 84 Spitzer - Seeing a New Ring Around Saturn 9-12 85 IBEX - Creating an Unusual Image of the Sky 6-8 86 8.0 Archiving Data for the Future Data Archiving Through the Ages 6-8 87 Data Migration from One Medium to the Next 6-8 88 Data Storage and Damage Control 6-8 89 9.0 Special Studies Hinode: Remote Sensing of Solar Plasma 6-8 90 Hinode: Close-up of an Active Region by X-ray Light 6-8 91 Hinode: Measuring Spectral Line Intensities 6-8 92 Hinode: Line Ratios and Plasma Temperature 9-12 93 Hinode: The Spectral Analysis of a Sunspot 6-8 94 Hinode: Plasma Temperature Across an Active Region 6-8 95 Landsat: Multi-Wavelength Imaging 6-8 96 Landsat: Identifying Thematic Content 6-8 97 Landsat: The Imager Geometry 6-8 98 Landsat: Creating 2-D Thematic Images 6-8 99 Space Math http://spacemath.gsfc.nasa.gov Table of Contents (cont'd) VI 10.0 Additional Resources for Beginners Creating an Image from Numbers 3-5 100 Interpreting a False-Color Image of Comet Tempel-1 3-5 101 Mapping the Speed of the Circinus Galaxy 3-5 102 Follow that Moving Star! 3-5 103 Additional Resources on the Web 104 Alignment with Standards The following benchmarks were extracted from 'AAAS Project: 2061: Benchmarks'. (3-5) - Quantities and shapes can be used to describe objects and events in the world around us. 2C/E1 --- Mathematics is the study of quantity and shape and is useful for describing events and solving practical problems. 2A/E1 (6-8) Mathematicians often represent things with abstract ideas, such as numbers or perfectly straight lines, and then work with those ideas alone. The "things" from which they abstract can be ideas themselves; for example, a proposition about "all equal-sided triangles" or "all odd numbers". 2C/M1 (9-12) - Mathematical modeling aids in technological design by simulating how a proposed system might behave. 2B/H1 ---- Mathematics provides a precise language to describe objects and events and the relationships among them. In addition, mathematics provides tools for solving problems, analyzing data, and making logical arguments. 2B/H3 ----- Much of the work of mathematicians involves a modeling cycle, consisting of three steps: (1) using abstractions to represent things or ideas, (2) manipulating the abstractions according to some logical rules, and (3) checking how well the results match the original things or ideas. The actual thinking need not follow this order. 2C/H2 Space Math http://spacemath.gsfc.nasa.gov Mathematics Topic Matrix VII Topic Problem Numbers 1 2 3 4 5 6 7 8 9 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 3 3 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 Inquiry Technology, rulers X X X X Numbers, X X X X X X X X X X patterns, percentages Averages X X X X X Time, distance, speed X X X X X X Areas and volumes X Scale drawings Geometry X X X X X X Probability, odds X X X Scientific Notation X X X X X Unit X X X X X X X X X Conversions Fractions X X Graph or Table Analysis X X X X X Pie Graphs Linear X X Equations Rates & Slopes X X X X X X X X X Solving for X X Evaluating Fns X X X X X X Modeling X Trigonometry Logarithms X X X Calculus Arrays or X X X X X matrices Conics
Load more

Recommended publications
  • As the Dome of Twilight Sinks Below The
    As the dome of twilight sinks below the horizon, a mechanical corps de ballet starts a slow-motion pirouette with each dancer keeping the unblinking eye of a telescope locked on a single spot in the heavens. Shutters open and ancient photons, ending a journey that may have started before the earth was born, collide with sensors that store an electron to mark that photon's arrival. With the dance in motion the directors sit back to watch the show; another imaging session has begun... Image by Marcus Stevens A Full and Proper Kit An introduction to the gear of astro-photography The young recruit is silly – 'e thinks o' suicide; 'E's lost his gutter-devil; 'e 'asn't got 'is pride; But day by day they kicks him, which 'elps 'im on a bit, Till 'e finds 'isself one mornin' with a full an' proper kit. Rudyard Kipling Like the young recruit in Kipling's poem 'The 'Eathen', a deep-sky imaging beginner starts with little in the way of equipment or skill. With 'older' imagers urging him onward, providing him with the benefit of the mistakes that they had made during their journey and allowing him access to the equipment they've built or collected, the newcomer gains the 'equipment' he needs, be it gear or skills, to excel at the art. At that time he has acquired a 'full and proper kit' and ceases to be a recruit. This paper is a discussion of hardware, software, methods and actions that a newcomer might find useful. It is not meant to be an in-depth discussion of all forms of astro-photography; that would take many books and more knowledge than I have available.
    [Show full text]
  • Canvas and Cosmos: Visual Art Techniques Applied to Astronomy Data
    March 14, 2017 0:27 WSPC/INSTRUCTION FILE EnglishJCanvasCos- mos International Journal of Modern Physics D c World Scientific Publishing Company Canvas and Cosmos: Visual Art Techniques Applied to Astronomy Data. JAYANNE ENGLISH∗ Department of Physics and Astronomy, University of Manitoba, Winnipeg, Manitoba, R3T 2N2, Canada. Jayanne [email protected] Received Day Month Year Revised Day Month Year Bold colour images from telescopes act as extraordinary ambassadors for research astronomers because they pique the public's curiosity. But are they snapshots docu- menting physical reality? Or are we looking at artistic spacescapes created by digitally manipulating astronomy images? This paper provides a tour of how original black and white data, from all regimes of the electromagnetic spectrum, are converted into the colour images gracing popular magazines, numerous websites, and even clothing. The history and method of the technical construction of these images is outlined. However, the paper focuses on introducing the scientific reader to visual literacy (e.g. human per- ception) and techniques from art (e.g. composition, colour theory) since these techniques can produce not only striking but politically powerful public outreach images. When cre- ated by research astronomers, the cultures of science and visual art can be balanced and the image can illuminate scientific results sufficiently strongly that the images are also used in research publications. Included are reflections on how they could feedback into astronomy research endeavours and future forms of visualization as well as on the rele- vance of outreach images to visual art. (See the colour online version, in which figures can be enlarged, at http://xxxxxxx.) Keywords: astronomy; astrophysics; public outreach; image-making; visualization; colour theory; art arXiv:1703.04183v1 [astro-ph.IM] 12 Mar 2017 PACS numbers: 1.
    [Show full text]
  • Bringing the Visible Universe Into Focus with Robo-AO
    Journal of Visualized Experiments www.jove.com Video Article Bringing the Visible Universe into Focus with Robo-AO Christoph Baranec1,2, Reed Riddle1, Nicholas M. Law3, A.N. Ramaprakash4, Shriharsh P. Tendulkar2, Khanh Bui1, Mahesh P. Burse4, Pravin Chordia4, Hillol K. Das4, Jack T.C. Davis1, Richard G. Dekany1, Mansi M. Kasliwal5, Shrinivas R. Kulkarni1,2, Timothy D. Morton2, Eran O. Ofek6, Sujit Punnadi4 1 Caltech Optical Observatories, California Institute of Technology 2 Department of Astronomy, California Institute of Technology 3 Dunlap Institute for Astronomy and Astrophysics, University of Toronto 4 Inter-University Centre for Astronomy & Astrophysics 5 Observatories of the Carnegie Institution for Science 6 Benoziyo Center for Astrophysics, Weizmann Institute of Science Correspondence to: Christoph Baranec at [email protected] URL: http://www.jove.com/video/50021 DOI: doi:10.3791/50021 Keywords: Physics, Issue 72, Astronomy, Mechanical Engineering, Astrophysics, Optics, Adaptive optics, lasers, wavefront sensing, robotics, stars, galaxies, imaging, supernova, telescopes Date Published: 2/12/2013 Citation: Baranec, C., Riddle, R., Law, N.M., Ramaprakash, A.N., Tendulkar, S.P., Bui, K., Burse, M.P., Chordia, P., Das, H.K., Davis, J.T.C., Dekany, R.G., Kasliwal, M.M., Kulkarni, S.R., Morton, T.D., Ofek, E.O., Punnadi, S. Bringing the Visible Universe into Focus with Robo-AO. J. Vis. Exp. (72), e50021, doi:10.3791/50021 (2013). Abstract The angular resolution of ground-based optical telescopes is limited by the degrading effects of the turbulent atmosphere. In the absence of an atmosphere, the angular resolution of a typical telescope is limited only by diffraction, i.e., the wavelength of interest, λ, divided by the size of its primary mirror's aperture, D.
    [Show full text]
  • PHY104 - Introduction to Astrophysics
    PHY104 - Introduction to Astrophysics S. P. Littlefair June 4, 2013 Chapter 1 Properties of Light 1.1 Introduction The only information we have about our Universe comes from the light emitted by objects within it. A good understanding of light is essential in all of astrophysics. We must learn what light is and how it behaves. We must understand it's properties, and learn how to use those properties to discover the information we seek. Finally, we must understand how light interacts with the matter around it. Much of the rest of the astrophysics course at Sheffield deals with what we know. By covering the basic physics of light, this course aims to explain how we acquire that knowledge. Our starting point is a question which seems quite simple; \what is light"? 1.2 The wave nature of light It is easy to demonstrate that light behaves like a wave. The famous Young's slit experiment is an elegant demonstration, and is shown in the left-hand side of figure 1.1. In this experiment, a thin plate with two parallel slits are illuminated by a single light source, and the light passing through the slits strikes a screen behind them. When we look on the screen, we see a diffraction pattern, made up of a series of bright and dark fringes. The diffraction pattern is easily understood if we think of light as a wave propa- gating through some medium, like water waves on a lake. In our experiment, each slit acts as a source of light waves; a wavefront of light spreads out from each slit.
    [Show full text]
  • Astrophotonics: Astronomy and Modern Optics
    Astrophotonics: Astronomy and modern optics S. Minardi AMS, G¨oschwitzer-Str. 32, 07745 Jena, Germany [email protected] R. Harris Zentrum f¨ur Astronomie der Universit¨at Heidelberg, Landessternwarte Ko¨nigstuhl, Ko¨nigstuhl 12, 69117 Heidelberg [email protected] L. Labadie I. Physikalisches Institut der Universit¨at zu K¨oln Z¨ulpicher Str. 77, 50937 K¨oln - Germany [email protected] Invited review article for The Astronomy and Astrophysics Review. Submitted on 9 Nov 2018 Abstract Much of the progress in Astronomy has been driven by instrumental developments, from the first telescopes to fiber fed spectrographs. In this review we describe the field of astrophotonics, a combination of photonics and astronomical instrumentation that is currently gaining importance in the development of current and future instrumentation. We begin with the science cases that have been identified as possibly benefiting from as- trophotonic devices. We then discuss devices, methods and developments in the field along with the advantages they provide. We conclude by de- scribing possible future developments in the field and their influence on astronomy. 1 Astronomical instrumentation and science arXiv:2003.12485v2 [astro-ph.IM] 8 Nov 2020 Astronomy is without doubt the empirical science which more than others relies on the analysis of electromagnetic radiation, and as such its progress has often been correlated to the development of optical technology. The most obvious example of the interaction between science and technology are the discoveries Galileo made at the beginning of the 17th century, by pointing his telescope, then the state of the art of optical instrumentation, at the sky.
    [Show full text]
  • J-PAS: the Javalambre-Physics of the Accelerated Universe Astrophysical Survey
    J-PAS: The Javalambre-Physics of the Accelerated Universe Astrophysical Survey N. Ben´ıteza,b, R. Dupkeb,c,d, M. Molese,a, L. Sodre´f, A. J. Cenarroe, A. Mar´ın-Franche, K. Taylorb, D. Cristobal´ e, A. Fernandez-Soto´ l, C. Mendes de Oliveiraf, J. Cepa-Nogue´h, L.R. Abramoi, J.S. Alcanizb, R. Overzierb, C. Hernandez-Monteagudo´ e, E. J. Alfaroa, A. Kanaanj, J. M. Carvanob, R. R. R. Reisk, E. Mart´ınez Gonzalez´ l, B. Ascasoa, F. Ballesterosg, H. S. Xavieri, J. Varelae, A. Ederoclitee, H. Vazquez´ Ramio´f, T. Broadhurstn, E. Cyprianof, R. Anguloe, J. M. Diegol, A. Zandivarez´ o, E. D´ıazo, P. Melchiorp, K. Umetsuq, P. F. Spinellir, A. Zitrins, D. Coean, G. Yepest, P. Vielval, V. Sahniu, A. Marcos-Caballerol, F. Shu Kitaurav, A. L. Marotow, M. Masipat, S. Tsujikawax, S. Carneiroy, J. Gonzalez´ Nuevol, G. C. Carvalhob, M. J. Rebouc¸asav, J. C. Carvalhob,z, E. Abdallai, A. Bernuib, C. Pigozzoy, E. G. M. Ferreirai, N. Chandrachani Devib, C. A. P. Bengaly Jr.b, M. Campistab, A. Amorimg, N. V. Asariaa, A. Bongiovannih, S. Bonolie, G. Bruzualab, N. Cardiell, A. Cavaac, R. Cid Fernandesj, P. Coelhoai, A. Cortesif, R. G. Delgadoa, L. D´ıaz Garciae, J. M. R. Espinosah, E. Gallianob, J. I. Gonzalez-Serrano´ l, J. Falcon-Barroso´ h, J. Fritzad, C. Fernandesb, J. Gorgasl, C. Hoyosf, Y. Jimenez-Teja´ a,b, J. A. Lopez-Aguerri´ h, C. Lopez-San´ Juane, A. Mateusj, A. Molinoa, P. Novaisf, A. O’Millf, I. Oteoh, P.G. Perez-Gonz´ alez´ l, B. Poggiantiaf, R.
    [Show full text]
  • A Precise Photometric Ratio Via Laser Excitation of the Sodium Layer I
    MNRAS 506, stab1621 (accepted advance article) (2021) Preprint 17 August 2021 Compiled using MNRAS LATEX style file v3.0 A precise photometric ratio via laser excitation of the sodium layer – I. One-photon excitation using 342.78 nm light Justin E. Albert ,1? Dmitry Budker ,2;4;5 Kelly Chance ,3 Iouli E. Gordon ,3 Felipe Pedreros Bustos ,2;6 Maxim Pospelov,1;7;‡ Simon M. Rochester 4 and H. R. Sadeghpour 3 1Department of Physics and Astronomy, University of Victoria, Victoria, British Columbia V8W 3P6, Canada 2Helmholtz Institute, Johannes Gutenberg-Universität Mainz, 55099 Mainz, Germany 3Harvard-Smithsonian Center for Astrophysics, Cambridge, Massachusetts 02138, USA 4Rochester Scientific LLC, El Cerrito, California 94530, USA 5Department of Physics, University of California, Berkeley, California 94720-7300, USA 6Laboratoire d’Astrophysique de Marseille (LAM), Université d’Aix-Marseille & CNRS, F-13388 Marseille, France 7Perimeter Institute of Theoretical Physics, Waterloo, Ontario N2L 2Y5, Canada ‡Now at School of Physics and Astronomy, University of Minnesota, Minneapolis, Minnesota 55455, USA Accepted 2021 June 3. Received 2021 June 3; in original form 2021 January 18 ABSTRACT The largest uncertainty on measurements of dark energy using type Ia supernovae is presently due to systematics from photometry; specifically to the relative uncertainty on photometry as a function of wavelength in the optical spectrum. We show that a precise constraint on relative photometry between the visible and near-infrared can be achieved at upcoming survey telescopes, such as at the Vera C. Rubin Observatory, via a laser source tuned to the 342.78 nm vacuum excitation wavelength of neutral sodium atoms.
    [Show full text]
  • Rothney Astrophysical Observatory the CMT-SQM Reported That the “Brightness” of the Sky Bottomed out Between 20.65 and 20.75 Magnitudes Per Square Arcsecond
    The Journal of The Royal Astronomical Society of Canada PROMOTING ASTRONOMY IN CANADA April/avril 2017 Volume/volume 111 Le Journal de la Société royale d’astronomie du Canada Number/numéro 2 [783] Inside this issue: Darkness over the RAO Short History of Astrophotography: Part 1 1994 St-Robert, Québec, Meteorite Gold dust April / avril 2017 JRASC | Promoting Astronomy in Canada i Research Articles / in the middle of the night to begin a late-night observing run, the SQM revealed what looked like a very dark Moonless sky Articles de recherche was actually brighter than the inside of the closed dome. And during this testing phase it was consistently found, Quantifying and Monitoring when detailed photometric calibrations were made of star fields when doing scientific work, that the photometric zeropoints in Darkness over the RAO the V filter came out quite close to what the SQM was measuring Phil Langill 1, 2 & Benjamin George 1 during the darkest part of the observing run. So the SQM actually lets one know what photometric limit to expect while 1 – University of Calgary observing. During the nicest darkest Moonless RAO nights 2 – Rothney Astrophysical Observatory the CMT-SQM reported that the “brightness” of the sky bottomed out between 20.65 and 20.75 magnitudes per square arcsecond. All things considered, the SQM is an awesome tool How dark is it? for quantifying the darkness of the nighttime sky. How dark is it? A basic question about a fundamental concept. And it’s a question that’s asked whenever people interested The Units of Radiance in seeing the stars get together.
    [Show full text]
  • Communications in Observations
    ＩＳＳＮ ０９１７－７３８８ COMMUNICATIONS IN CMO Since 1986 MARS No.376 25 September 2010 OBSERVATIONS No.02 PublishedbytheInternational Society of the Mars Observers Mars Above the Dreaming Spires: John Phillips and the First Globe of Mars By William SHEEHAN During the first week of August this year, I participated in a fascinating Stellafane pre-conference on Lunar Morphology fea- turing authorities such as Peter Schultz, Chuck Wood, Ron Doel, and Tom Dobbins. A number of geologists who contributed to the understanding of the morphology of the lunar features were discussed; so, when Dr. Minami asked me to contribute an article on the history of Mars studies for the next issue of ISMO, I decided to recall the career of the first professional geologist to make a detailed study of Mars. A hundred fifty years ago, John Phillips, professor of geology at Oxford, ordered a 6½-inch Cooke refractor that, when deliv- ered in 1862, he set up near the Oxford Museum of Natural History and used to observe Mars at the splendid opposition of that year. These observations served as the basis of the first globe of Mars ever constructed, a forerunner of those by Camille Flammarion, Percival Lowell, and Greg Mort some of us admired at the One Century of Mars Observations conference in Paris last year. I present this paper to my fellow readers of ISMO in celebration of the (almost) sesquicentennial celebration of the first globe of Mars. n June 30, 1860, seven months after the pub‐ one of his incessant illnesses;(1) but the seven hun‐ Olication of Charles Darwin’s Origin of Species, dred who were there included notables such as the British Association for the Advancement of Sci‐ Robert Fitzroy, commander of the Beagle during the ence (BAAS) met in the new University Museum, circumnavigation of the globe on which Darwin which houses the teaching collections of the six hadservedasnaturalist,andDarwin’salliesJoseph professors of Natural Science.
    [Show full text]
  • Download Paper
    The Gaia Catalogue Second Data Release and its Implications to Optical Observations of Man-made Earth Orbiting Objects James Frith University of Texas El Paso Jacobs JETS Contract, NASA Johnson Space Center 2224 Bay Area Blvd, Houston, TX 77058 ABSTRACT The Gaia spacecraft was launched in December 2013 by the European Space Agency to produce a three- dimensional, dynamic map of objects within the Milky Way. Gaia’s first year of data was released in September 2016. Common sources from the first data release have been combined with the Tycho-2 catalogue to provide a 5-parameter astrometric solution for approximately 2 million stars. The second Gaia data release, made public in April 2018, provides astrometry and photometry for more than 1 billion stars; a subset of which contains the full 6-parameter astrometric solution (adding radial velocity) and positional accuracy better than 0.002 arcsec (2 mas). In addition to precise astrometry, a unique feature of the Gaia catalogue is its production of accurate, broadband photometry using the Gaia G-band. In the past, clear filters have been used by various groups to maximize likelihood of detection of dim man-made objects but these data were very difficult to calibrate. With the second release of the Gaia catalogue, a ground-based system utilizing the G-band filter will have access to 1.5 billion all- sky calibration sources down to an accuracy of 0.02 magnitudes or better. We discuss the advantages and practicalities of implementing the Gaia filters and its associated catalogue into data pipelines designed for optical observations of man-made objects.
    [Show full text]
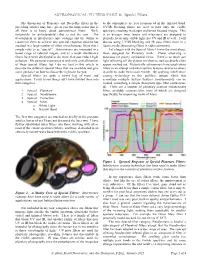
  • Special Filters
    ASTRONOMICAL FILTERS PART 4: Special Filters My discussion of Planetary and Deep-Sky filters in the to the atmosphere are less pronounced in the infrared band. preceding articles may have given you the impression that is UV/IR blocking filters are used to pass only the visible all there is to know about astronomical filters. Well, spectrum, resulting in sharper and better focused images. This fortunately (or unfortunately!) that is not the case. The is so because most lenses and telescopes are designed to development of interference type coatings and the ability to properly focus only visible light, not UV and IR as well. I will customize them to achieve any spectral response desired has discuss using UV/IR blocking and IR pass filters more in a resulted in a large number of other miscellaneous filters that I future article about using filters in video astronomy. simply refer to as “special”. Astronomers are interested in a Let’s begin with the Special filters I know the most about, broad range of celestial targets, and as a result interference those designed for Planetary work. Planet observing is filters have been developed to do more than just reduce light notorious for poorly contrasted views. There is so much sun pollution. My personal experience is with only a small number light reflecting off the planets we observe, surface details often of these special filters, but I do my best in this article to appear washed out. Historically astronomers have used colour describe the different special filters that are available and give filters in an attempt to darken surface features relative to others some guidance on how to choose the right one for you.
    [Show full text]
  • TOROS Optical Follow-Up of the Advanced LIGO-VIRGO O2 Second Observational Campaign
    MNRAS 000,1{9 (2018) Preprint 11 January 2019 Compiled using MNRAS LATEX style file v3.0 TOROS Optical follow-up of the Advanced LIGO-VIRGO O2 second observational campaign Rodolfo Artola,1 Martin Beroiz,2 Juan Cabral,1 Richard Camuccio,2 Moises Castillo,2 Vahram Chavushyan,3 Carlos Colazo,1 Hector Cuevas Larenas,4 Darren L. DePoy,5 Mario C. D´ıaz,2 Mariano Dom´ınguez,1 Deborah Dultzin,6 Daniela Fern´andez,7 Antonio C. Ferreyra,1 Aldo Fonrouge,2 Jos´eFranco,6 Dar´ıo Gra~na,1 Carla Girardini,1 Sebasti´an Gurovich,1 Antonio Kanaan,8 Diego G. Lambas,1 Marcelo Lares,1 Alejandro F. Hinojosa,2 Andrea Hinojosa,2 Americo F. Hinojosa,2 Omar L´opez-Cruz,3 Lucas M. Macri,5 Jennifer L. Marshall,5 Raul Melia,1 Wendy Mendoza,2 Jos´eL. Nilo Castell´on4;9, Nelson Padilla,7 Victor Perez,2 Tania Pe~nuela,2 Wahltyn Rattray,1 V´ıctor Renzi,1 Emmanuel R´ıos-L´opez,3 Amelia Ram´ırez Rivera,4 Tiago Ribeiro,10 Horacio Rodriguez,1 Bruno S´anchez,1 Mat´ıas Schneiter,1 William Schoenell,11 Manuel Starck,1 Rub´enVrech,1 Cecilia Qui~nones,1 Luis Tapia,1 Marina Tornatore,1 Sergio Torres-Flores,4 Ervin Vilchis,2 Adam Zadro_zny2;12? 1Universidad Nacional de C´ordoba, IATE, C´ordoba, Argentina 2Center for Gravitational Wave Astronomy, The University of Texas Rio Grande Valley, Brownsville, TX, USA 3Instituto Nacional de Astrof´ısica, Optica´ y Electr´onica, Tonantzintla, Puebla, M´exico 4Departamento de F´ısica y Astronom´ıa,Universidad de La Serena, La Serena, Chile 5George P.
    [Show full text]