A Variation on the Damped LC Circuit: Back-To-Back Diodes
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Optoelectronic Oscillators: Recent and Emerging Trends Optoelectronic Oscillators: Recent and Emerging Trends
Optoelectronic Oscillators: Recent and Emerging Trends Optoelectronic Oscillators: Recent and Emerging Trends October 11, 2018 Afshin S. Daryoush(1), Ajay Poddar(2), Tianchi Sun(1), and Ulrich L. Rohde(2), Drexel University(1); Synergy Microwave(2) Highly stable oscillators are key components in many important applications where coherent processing is performed for improved detection. The optoelectronic oscillator (OEO) exhibits low phase noise at microwave and mmWave frequencies, which is attractive for applications such as synthetic aperture radar, space communications, navigation and meteorology, as well as for communications carriers operating at frequencies above 10 GHz, with the advent of high data rate wireless for high speed data transmission. The conventional OEO suffers from a large number of unwanted, closely-spaced oscillation modes, large size and thermal drift. State-of-the- art performance is reported for X- and K-Band OEO synthesizers incorporating a novel forced technique of self-injection locking, double self phase-locking. This technique reduces phase noise both close-in and far-away from the carrier, while suppressing side modes observed in standard OEOs. As an example, frequency synthesizers at X-Band (8 to 12 GHz) and K-Band (16 to 24 GHz) are demonstrated, typically exhibiting phase noise at 10 kHz offset from the carrier better than −138 and −128 dBc/Hz, respectively. A fully integrated version of a forced tunable low phase noise OEO is also being developed for 5G applications, featuring reduced size and power consumption, less sensitivity to environmental effects and low cost. Electronic oscillators generate low phase noise signals up to a few GHz but suffer phase noise degradation at higher frequencies, principally due to low Q-factor resonators. -

Analysis of BJT Colpitts Oscillators - Empirical and Mathematical Methods for Predicting Behavior Nicholas Jon Stave Marquette University
Marquette University e-Publications@Marquette Master's Theses (2009 -) Dissertations, Theses, and Professional Projects Analysis of BJT Colpitts Oscillators - Empirical and Mathematical Methods for Predicting Behavior Nicholas Jon Stave Marquette University Recommended Citation Stave, Nicholas Jon, "Analysis of BJT Colpitts sO cillators - Empirical and Mathematical Methods for Predicting Behavior" (2019). Master's Theses (2009 -). 554. https://epublications.marquette.edu/theses_open/554 ANALYSIS OF BJT COLPITTS OSCILLATORS – EMPIRICAL AND MATHEMATICAL METHODS FOR PREDICTING BEHAVIOR by Nicholas J. Stave, B.Sc. A Thesis submitted to the Faculty of the Graduate School, Marquette University, in Partial Fulfillment of the Requirements for the Degree of Master of Science Milwaukee, Wisconsin August 2019 ABSTRACT ANALYSIS OF BJT COLPITTS OSCILLATORS – EMPIRICAL AND MATHEMATICAL METHODS FOR PREDICTING BEHAVIOR Nicholas J. Stave, B.Sc. Marquette University, 2019 Oscillator circuits perform two fundamental roles in wireless communication – the local oscillator for frequency shifting and the voltage-controlled oscillator for modulation and detection. The Colpitts oscillator is a common topology used for these applications. Because the oscillator must function as a component of a larger system, the ability to predict and control its output characteristics is necessary. Textbooks treating the circuit often omit analysis of output voltage amplitude and output resistance and the literature on the topic often focuses on gigahertz-frequency chip-based applications. Without extensive component and parasitics information, it is often difficult to make simulation software predictions agree with experimental oscillator results. The oscillator studied in this thesis is the bipolar junction Colpitts oscillator in the common-base configuration and the analysis is primarily experimental. The characteristics considered are output voltage amplitude, output resistance, and sinusoidal purity of the waveform. -
C I L Q LC Circuit
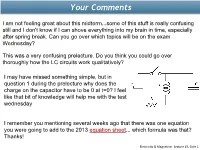
Your Comments I am not feeling great about this midterm...some of this stuff is really confusing still and I don't know if I can shove everything into my brain in time, especially after spring break. Can you go over which topics will be on the exam Wednesday? This was a very confusing prelecture. Do you think you could go over thoroughly how the LC circuits work qualitatively? I may have missed something simple, but in question 1 during the prelecture why does the charge on the capacitor have to be 0 at t=0? I feel like that bit of knowledge will help me with the test wednesday I remember you mentioning several weeks ago that there was one equation you were going to add to the 2013 equation sheet... which formula was that? Thanks! Electricity & Magnetism Lecture 19, Slide 1 Some Exam Stuff Exam Wed. night (March 27th) at 7:00 Covers material in Lectures 9 – 18 Bring your ID: Rooms determined by discussion section (see link) Conflict exam at 5:15 Don’t forget: • Worked examples in homeworks (the optional questions) • Other old exams For most people, taking old exams is most beneficial Final Exam dates are now posted The Big Ideas L9-18 Kirchoff’s Rules Sum of voltages around a loop is zero Sum of currents into a node is zero Kirchoff’s rules with capacitors and inductors • In RC and RL circuits: charge and current involve exponential functions with time constant: “charging and discharging” Q dQ Q • E.g. IR R V C dt C Capacitors and inductors store energy Magnetic fields Generated by electric currents (no magnetic charges) Magnetic -

Silicon Bipolar Distributed Oscillator Design and Analysis
Science World Journal Vol 9 (No 4) 2014 www.scienceworldjournal.org ISSN 1597-6343 SILICON BIPOLAR DISTRIBUTED OSCILLATOR DESIGN AND ANALYSIS Article Research Full Length Aku, M. O. and *Imam, R. S. Department of Physics, Bayero University, Kano-Nigeria * Department of Physics, Kano University of Science and Technology, Wudil-Nigeria ABSTRACT between its input and output. It can be shown that there is a The design of high frequency silicon bipolar oscillator using trade-off between the bandwidth and delay in an amplifier common emitter (CE) with distributed output and analysis is (Lee, 1998). Distributed amplification provides a means to carried out. The general condition for oscillation and the take advantage of this trade-off in applications where the resulting analytical expressions for the frequency of delay is not a critical specification of the system and can be oscillators were reviewed. Transmission line design was compromised in favour of the bandwidth (distributed carried out using Butterworth LC filters in which the oscillator). It is noteworthy that the physical size of a normalised values and where used to obtain the distributed amplifier does not have to be comparable to the actual values of the inductors and capacitors used; this wavelength for it to enhance the bandwidth. Dividing the gain largely determines the performance of distributed oscillators. between multiple active devices avoids the concentration of The values of inductor and capacitors in the phase shift the parasitic at one place and hence eliminates a dominant network are used in tuning the oscillator. The simulated pole scenario in the frequency domain transfer function. -

Analysis of Magnetic Resonance in Metamaterial Structure
Analysis of magnetic resonance in Metamaterial structure Rajni#1, Anupma Marwaha#2 #1 Asstt. Prof. Shaheed Bhagat Singh College of Engg. And Technology,Ferozepur(Pb.)(India), #2 Assoc. Prof., Sant Longowal Institute of Engg. And Technology,Sangrur(Pb.)(India) [email protected] 2 [email protected] Abstract: ‘Metamaterials’ is one of the most 1. Introduction recent topics in several areas of science and technology due to its vast potential in various Metamaterials are artificial materials synthesized applications. These are artificially fabricated by embedding specific inclusions like periodic materials which exhibit negative permittivity structures in host media. These materials have and/or negative permeability. The unusual the unique property of negative permittivity electromagnetic properties of metamaterial and/or negative permeability not encountered in have opened more opportunities for better the nature. If materials have both parameters antenna design to surmount the limitations of negative at the same time, then they exhibit an conventional antennas. Metamaterials have effective negative index of refraction and are created many designs in a broad frequency referred to as Left-Handed Metamaterials spectrum from microwave to millimeter wave (LHM). This name is given to these materials to optical structures. The edifice building because the electric field, magnetic field and the blocks of metamaterials are synthetically wave vector form a left-handed system. These fabricated periodic structures of having materials offer a new dimension to the antenna lattice constants smaller than the wavelength applications. The phase velocity and group of the incident radiation. Thus metamaterial velocity in these materials are anti-parallel to properties can be controlled by the design of each other i.e. -

Durham Research Online
Durham Research Online Deposited in DRO: 07 November 2018 Version of attached le: Accepted Version Peer-review status of attached le: Peer-reviewed Citation for published item: Brennan, D.R. and Chan, H.K. and Wright, N.G. and Horsfall, A.B. (2018) 'Silicon carbide oscillators for extreme environments.', in Low power semiconductor devices and processes for emerging applications in communications, computing, and sensing. Boca Raton, FL: CRC Press, pp. 225-252. Devices, circuits, and systems. Further information on publisher's website: https://doi.org/10.1201/9780429503634-10 Publisher's copyright statement: This is an Accepted Manuscript of a book chapter published by Routledge in Low power semiconductor devices and processes for emerging applications in communications, computing, and sensing on 31 July 2018 available online: http://www.routledge.com/9780429503634 Additional information: Use policy The full-text may be used and/or reproduced, and given to third parties in any format or medium, without prior permission or charge, for personal research or study, educational, or not-for-prot purposes provided that: • a full bibliographic reference is made to the original source • a link is made to the metadata record in DRO • the full-text is not changed in any way The full-text must not be sold in any format or medium without the formal permission of the copyright holders. Please consult the full DRO policy for further details. Durham University Library, Stockton Road, Durham DH1 3LY, United Kingdom Tel : +44 (0)191 334 3042 | Fax : +44 (0)191 334 2971 https://dro.dur.ac.uk Silicon Carbide Oscillators for Extreme Environments D.R. -

Quartz Resonator & Oscillator Tutorial
Rev. 8.5.3.6 Quartz Crystal Resonators and Oscillators For Frequency Control and Timing Applications - A Tutorial January 2007 John R. Vig Consultant. Most of this Tutorial was prepared while the author was employed by the US Army Communications-Electronics Research, Development & Engineering Center Fort Monmouth, NJ, USA [email protected] Approved for public release. Distribution is unlimited NOTICES Disclaimer The citation of trade names and names of manufacturers in this report is not to be construed as official Government endorsement or consent or approval of commercial products or services referenced herein. Table of Contents Preface………………………………..……………………….. v 1. Applications and Requirements………………………. 1 2. Quartz Crystal Oscillators………………………………. 2 3. Quartz Crystal Resonators……………………………… 3 4. Oscillator Stability………………………………………… 4 5. Quartz Material Properties……………………………... 5 6. Atomic Frequency Standards…………………………… 6 7. Oscillator Comparison and Specification…………….. 7 8. Time and Timekeeping…………………………………. 8 9. Related Devices and Applications……………………… 9 10. FCS Proceedings Ordering, Website, and Index………….. 10 iii Preface Why This Tutorial? “Everything should be made as simple as I was frequently asked for “hard-copies” of possible - but not simpler,” said Einstein. The the slides, so I started organizing, adding main goal of this “tutorial” is to assist with some text, and filling the gaps in the slide presenting the most frequently encountered collection. As the collection grew, I began concepts in frequency control and timing, as receiving favorable comments and requests simply as possible. for additional copies. Apparently, others, too, found this collection to be useful. Eventually, I I have often been called upon to brief assembled this document, the “Tutorial”. visitors, management, and potential users of precision oscillators, and have also been This is a work in progress. -

UNIVERSITY of NEVADA, RENO Introduction to Quartz Resonator
UNIVERSITY OF NEVADA, RENO Introduction to Quartz Resonator Based Electronic Oscillators and Development of Electronic Oscillators Using Inverted-Mesa Etched Quartz Resonators A thesis submitted on partial fulfillment of the requirements for the degree of MASTER OF SCIENCE IN ELECTRICAL ENGINEERING By Matthew B. Anthony Thesis Advisor Dr. Indira Chatterjee August 2009 Copyright by Matthew B. Anthony 2009 All Rights Reserved THE GRADUATE SCHOOL We recommend that the thesis prepared under our supervision by MATTHEW B. ANTHONY entitled Introduction To Quartz Resonator Based Electronic Oscillators And Development Of Electronic Oscillators Using Inverted-Mesa Etched Quartz Resonators be accepted in partial fulfillment of the requirements for the degree of MASTER OF SCIENCE Indira Chatterjee, Ph.D., Advisor Bruce P. Johnson, Ph.D., Committee Member Scott Talbot, M.S., Committee Member Ronald Phaneuf, Ph.D., Graduate School Representative Marsha H. Read, Ph. D., Associate Dean, Graduate School August, 2009 i ABSTRACT The current work is primarily focused on the topic of the advancement of low phase noise and low jitter quartz crystal based electronic oscillators to frequencies beyond those presently available using quartz resonators that are manufactured using the traditional method that processes the entire sample to a uniform thickness. The method of inverted-mesa etching allows the resonant part of the quartz sample to be made much thinner than the remainder of the sample – enabling higher resonant frequencies to be achieved. The current work will introduce and discuss the importance of phase noise and jitter in electronic oscillator applications such as wireless communication systems and sampled data systems. General oscillator and quartz resonator background will be provided to facilitate the understanding of the oscillator circuit used herein. -

6.453 Quantum Optical Communication Reading 4
Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.453 Quantum Optical Communication Lecture Number 4 Fall 2016 Jeffrey H. Shapiro c 2006, 2008, 2014, 2016 Date: Tuesday, September 20, 2016 Reading: For the quantum harmonic oscillator and its energy eigenkets: C.C. Gerry and P.L. Knight, Introductory Quantum Optics (Cambridge Uni- • versity Press, Cambridge, 2005) pp. 10{15. W.H. Louisell, Quantum Statistical Properties of Radiation (McGraw-Hill, New • York, 1973) sections 2.1{2.5. R. Loudon, The Quantum Theory of Light (Oxford University Press, Oxford, • 1973) pp. 128{133. Introduction In Lecture 3 we completed the foundations of Dirac-notation quantum mechanics. Today we'll begin our study of the quantum harmonic oscillator, which is the quantum system that will pervade the rest of our semester's work. We'll start with a classical physics treatment and|because 6.453 is an Electrical Engineering and Computer Science subject|we'll develop our results from an LC circuit example. Classical LC Circuit Consider the undriven LC circuit shown in Fig. 1. As in Lecture 2, we shall take the state variables for this system to be the charge on its capacitor, q(t) Cv(t), and the flux through its inductor, p(t) Li(t). Furthermore, we'll consider≡ the behavior of this system for t 0 when one≡ or both of the initial state variables are non-zero, i.e., q(0) = 0 and/or≥p(0) = 0. You should already know that this circuit will then undergo simple6 harmonic motion,6 i.e., the energy stored in the circuit will slosh back and forth between being electrical (stored in the capacitor) and magnetic (stored in the inductor) as the voltage and current oscillate sinusoidally at the resonant frequency ! = 1=pLC. -

Wideband Tunable Microwave Signal Generation in a Silicon-Based Optoelectronic Oscillator
Wideband tunable microwave signal generation in a silicon-based optoelectronic oscillator Phuong T.Do1,*, Carlos Alonso-Ramos2, Xavier Le Roux2, Isabelle Ledoux1, Bernard Journet1, and Eric Cassan2 1LPQM (CNRS UMR-8537,Ecole´ normale superieure´ Paris-Saclay, Universite´ Paris-Saclay, 61 avenue du President´ Wilson, 94235 Cachan Cedex, France 2C2N (CNRS UMR-9001), Univ. Paris-Sud, Universite´ Paris-Saclay, 10 Boulevard Thomas Gobert, 91120 Palaiseau, France *[email protected] ABSTRACT Si photonics has an immense potential for the development of compact and low-loss opto-electronic oscillators (OEO), with applications in radar and wireless communications. However, current Si OEO have shown a limited performance. Si OEO relying on direct conversion of intensity modulated signals into the microwave domain yield a limited tunability. Wider tunability has been shown by indirect phase-modulation to intensity-modulation conversion, requiring precise control of the phase-modulation. Here, we propose a new approach enabling Si OEOs with wide tunability and direct intensity-modulation to microwave conversion. The microwave signal is created by the beating between an optical source and single sideband modulation signal, selected by an add-drop ring resonator working as an optical bandpass filter. The tunability is achieved by changing the wavelength spacing between the optical source and resonance peak of the resonator. Based on this concept, we experimentally demonstrate microwave signal generation between 6 GHz and 18 GHz, the widest range for a Si-based OEO. Moreover, preliminary results indicate that the proposed Si OEO provides precise refractive index monitoring, with a sensitivity of 94350 GHz/RIU and a 8 potential limit of detection of only 10− RIU, opening a new route for the implementation of high-performance Si photonic sensors. -

How to Design Analog Filter Circuits.Pdf
a b FIG. 1-TWO LOWPASS FILTERS. Even though the filters use different components, they perform in a similiar fashion. MANNlE HOROWITZ Because almost every analog circuit contains some filters, understandinghow to work with them is important. Here we'll discuss the basics of both active and passive types. THE MAIN PURPOSE OF AN ANALOG FILTER In addition to bandpass and band- age (because inductors can be expensive circuit is to either pass or reject signals rejection filters, circuits can be designed and hard to find); they are generally easier based on their frequency. There are many to only pass frequencies that are either to tune; they can provide gain (and thus types of frequency-selective filter cir- above or below a certain cutoff frequency. they do not necessarily have any insertion cuits; their action can usually be de- If the circuit passes only frequencies that loss); they have a high input impedance, termined from their names. For example, are below the cutoff, the circuit is called a and have a low output impedance. a band-rejection filter will pass all fre- lo~~passfilter, while a circuit that passes A filter can be in a circuit with active quencies except those in a specific band. those frequencies above the cutoff is a devices and still not be an active filter. Consider what happens if a parallel re- higlzpass filter. For example, if a resonant circuit is con- sonant circuit is connected in series with a All of the different filters fall into one . nected in series with two active devices signal source. -

Oscilators Simplified
SIMPLIFIED WITH 61 PROJECTS DELTON T. HORN SIMPLIFIED WITH 61 PROJECTS DELTON T. HORN TAB BOOKS Inc. Blue Ridge Summit. PA 172 14 FIRST EDITION FIRST PRINTING Copyright O 1987 by TAB BOOKS Inc. Printed in the United States of America Reproduction or publication of the content in any manner, without express permission of the publisher, is prohibited. No liability is assumed with respect to the use of the information herein. Library of Cangress Cataloging in Publication Data Horn, Delton T. Oscillators simplified, wtth 61 projects. Includes index. 1. Oscillators, Electric. 2, Electronic circuits. I. Title. TK7872.07H67 1987 621.381 5'33 87-13882 ISBN 0-8306-03751 ISBN 0-830628754 (pbk.) Questions regarding the content of this book should be addressed to: Reader Inquiry Branch Editorial Department TAB BOOKS Inc. P.O. Box 40 Blue Ridge Summit, PA 17214 Contents Introduction vii List of Projects viii 1 Oscillators and Signal Generators 1 What Is an Oscillator? - Waveforms - Signal Generators - Relaxatton Oscillators-Feedback Oscillators-Resonance- Applications--Test Equipment 2 Sine Wave Oscillators 32 LC Parallel Resonant Tanks-The Hartfey Oscillator-The Coipltts Oscillator-The Armstrong Oscillator-The TITO Oscillator-The Crystal Oscillator 3 Other Transistor-Based Signal Generators 62 Triangle Wave Generators-Rectangle Wave Generators- Sawtooth Wave Generators-Unusual Waveform Generators 4 UJTS 81 How a UJT Works-The Basic UJT Relaxation Oscillator-Typical Design Exampl&wtooth Wave Generators-Unusual Wave- form Generator 5 Op Amp Circuits