Delivery and Pitch Type Alter Ground Reaction Forces in Baseball Pitching
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The BG News April 17, 2002
Bowling Green State University ScholarWorks@BGSU BG News (Student Newspaper) University Publications 4-17-2002 The BG News April 17, 2002 Bowling Green State University Follow this and additional works at: https://scholarworks.bgsu.edu/bg-news Recommended Citation Bowling Green State University, "The BG News April 17, 2002" (2002). BG News (Student Newspaper). 6953. https://scholarworks.bgsu.edu/bg-news/6953 This work is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 4.0 License. This Article is brought to you for free and open access by the University Publications at ScholarWorks@BGSU. It has been accepted for inclusion in BG News (Student Newspaper) by an authorized administrator of ScholarWorks@BGSU. 4^ ^A M ^ Bowling Green State University WEDNESDAY April 17, 2002 T-STORMS Falcons beat Defiance L J W ■ L HIGH: 77 I LOW: 54 College 8-3; PAGE 8 S JL 1 JLJ I I Fv V www.bgnews.com VOLUME 93 ISSUE 55 "Who wants to be Indiana inside?" JOHNNIE HARRISON, NY RESIDENT U.prof. * discusses Heat changes wave ■ in media IH v.- 11 THE BG NEWS brings Times have changed in newspaper wriling over the last few centuries, according to I 1 m- -j&imM-r. David Nord, a journalism pro- ■ 1 i.xm record fessor at Indiana University. Nord spoke at the University ~i ??M yesterday on news and religion in early American journalism. "Mrs. Dyer Brought Forth • highs Her Horned, Four-Taloned -4 I Monster," is a headline that many people today would look By Roger Petterson at with wondering amaze- THE ASSOCIATED PRESS ment. -

2018 Media Guide.Indd
HISTORY & RECORDS BISONS HISTORY & RECORDS BUFFALO BISONS RETIRED NUMBERS OLLIE CARNEGIE #6 Carnegie was the most popular player and greatest off ensive performer in the history of professional baseball in Buff alo. He played 12 years with the Bisons (1931-1941, 1945) and is Buff alo’s all-time leader with 258 home runs (2nd in International League behind only Mike Hessman) and 1,044 RBI. Carnegie led the Bisons in home runs and RBI seven times (1932-1935, 1937-1939) and the IL twice (1938, 1939). His 45 home runs in 1938 remain a club record. A lifetime .308 hitter, Carnegie also owns the Bisons records for games (1,273), hits (1,362) and doubles (249) even though he didn’t join the team until he was 32 years old. Carnegie was in the inaugural class for both the International League (1947) and Buff alo Baseball Hall of Fame. LUKE EASTER #25 Luscious Easter was a slugging fi rst baseman whose long home runs and colorful style of play captured the hearts of Bisons fans from 1956 through 1959. Easter, who was the fi rst black player to play for Buff alo since 1888, hit over 35 homers and drove more than 100 runs for three consecutive seasons in Buff alo. He led the International League in home runs at RBI in both 1956 (35 homers, 106 RBI) and 1957 (40 home runs, 128 RBI). All told, Easter hit 114 home runs and drove in 353 runs with the Bisons. Of his many memorable games, Easter will always be remembered as the fi rst player ever to hit a home run over the scoreboard at Off ermann Stadium. -

PDF Fantasy Preview
Catcher $$ First Base $$ Third Base $$ Outfield $$ Outfield $$ SP $$ SP $$ RP $$ Victor Martinez 28 Mark Teixeira 35 Alex Rodriguez 46 Vladimir Guerrero 40 Trot Nixon 7 Johan Santana 36 Rodrigo Lopez 4 Mariano Rivera 35 Joe Mauer 23 David Ortiz 33 Chone Figgins 30 Carl Crawford 36 Matt Lawton 7 Randy Johnson 29 Zack Greinke 4 Joe Nathan 32 Jason Varitek 21 Travis Hafner 31 Eric Chavez 27 Manny Ramirez 34 Alex Rios 7 Rich Harden 27 Gustavo Chacin 4 Francisco Rodriguez 32 Jorge Posada 17 Paul Konerko 29 Jorge Cantu 23 Ichiro Suzuki 32 Corey Patterson 7 Josh Beckett 26 Shawn Chacon 4 B.J. Ryan 30 Javy Lopez 16 Richie Sexson 29 Hank Blalock 22 Chone Figgins 30 Delmon Young 6 Felix Hernandez 26 Vicente Padilla 4 Huston Street 28 Ramon Hernandez 16 Jason Giambi 26 Melvin Mora 21 Hideki Matsui 28 Emil Brown 5 Roy Halladay 26 Roman Colon 4 Francisco Cordero 27 Kenji Johjima 14 Aubrey Huff 21 Troy Glaus 21 Gary Sheffield 28 Juan Rivera 5 John Lackey 24 Jason Johnson 4 Eddie Guardado 25 Ivan Rodriguez 13 Jim Thome 20 Adrian Beltre 14 Grady Sizemore 27 Shannon Stewart 4 A.J. Burnett 23 Josh Towers 4 Bobby Jenks 24 Benjie Molina 12 Brad Wilkerson 16 Shea Hillenbrand 13 Johnny Damon 26 Jason Michaels 4 Curt Schilling 21 Kenny Rogers 4 Keith Foulke 22 Rod Barajas 11 Lyle Overbay 16 Joe Crede 9 Vernon Wells 24 Casey Blake 3 Mark Buehrle 20 Nate Robertson 4 Todd Jones 22 A.J. Pierzynski 11 Dan Johnson 16 Mike Lowell 9 Scott Podsednik 24 Lew Ford 3 Kelvim Escobar 19 Kyle Lohse 4 Bob Wickman 20 Jason Kendall 9 Mike Sweeney 16 Kevin Youkilis 8 Coco Crisp 23 Brian Anderson 3 Barry Zito 18 Joel Piniero 4 Mike MacDougal 19 Toby Hall 5 Jay Gibbons 15 B.J. -

The Value of Youth in Major League Baseball
Claremont Colleges Scholarship @ Claremont CMC Senior Theses CMC Student Scholarship 2011 The alueV of Youth in Major League Baseball Jason Lee Claremont McKenna College Recommended Citation Lee, Jason, "The alueV of Youth in Major League Baseball" (2011). CMC Senior Theses. Paper 203. http://scholarship.claremont.edu/cmc_theses/203 This Open Access Senior Thesis is brought to you by Scholarship@Claremont. It has been accepted for inclusion in this collection by an authorized administrator. For more information, please contact [email protected]. CLAREMONT MCKENNA COLLEGE THE VALUE OF YOUTH IN MAJOR LEAGUE BASEBALL SUBMITTED TO JAY MARTIN AND RON RIGGIO AND DEAN GREGORY HESS BY JASON LEE FOR SENIOR THESIS FALL 2010/SPRING 2011 APRIL 25, 2011 Acknowledgements First, I want to thank my faculty readers, Professors Jay Martin and Ron Riggio, for their support, teachings, and confidence in my abilities. Thank you to my brother, Eddie, for introducing me to the world of sports. The source of my passion can be traced to his influence. Thank you to Matthew Moone (CMC ’09), whose senior thesis was instrumental in the development of my own thesis. And finally, a special thank you to Jayson Stark for taking the time to answer my e-mails and phone calls. I will always remember our conversation as one of the highlights of my life, as a sports fan. Thank you so much. Table of Contents I. Introduction II. Chapter 1 – History of the Youth Movement a. Steroids and Performance enhancing drugs b. The Effects of Drug Testing c. History of Free Agency d. Free Agency Today e. -
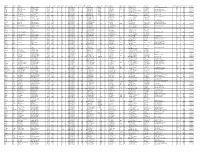
Lastname Firstname Realname Place Ht Wt Bats Throws Posit Year Phase Draftround Overall Teamid Teamname Bonus Posit Hscollege Pa
lastName firstname realname place ht wt bats throws posit year phase draftRound overall teamID teamname bonus posit hsCollege pageName highLevel region bornDate hsname hsLocation CollegeName mlbYears highLevel lastActiveY debut playYears Ames Jeff Jeffrey Ames Vancouver,Washington 4-Jun 220 R R P 2011 June-Reg 1 42 28 Tampa Bay Rays 650000 P C Jeffrey-Ames Rookie WA 1/31/1991 Skyview Vancouver,WA Lower Columbia Community College - RK 2011 2011-2011 Snell Blake Blake A. Snell Seattle,Washington 4-Jun 180 L L P 2011 June-Reg 1 52 28 Tampa Bay Rays 684000 P H blake-snell Rookie WA 12/4/1992 Shorewood Shoreline,WA - - RK 2011 2011-2011 Conley Adam Adam Michael Conley Olympia,Washington 3-Jun 170 L L P 2011 June-Reg 2 72 12 Florida Marlins 625000 P C Adam-Conley Rookie WA 5/24/1990 Olympia Olympia,WA Washington State University - RK 2011 2009-2011 Hebner Cody Cody Hebner Auburn,Washington 11-May 175 R R P 2011 June-Reg 4 143 24 San Diego Padres 200000 P C cody-hebner A- WA 11/21/1990 Auburn Mountainview Auburn,WA Green River Community College - A- 2011 2011-2011 Martin Cody Cody Martin Dos Palos,California 2-Jun 200 R R P 2011 June-Reg 7 236 3 Atlanta Braves 45000 P C Cody-Martin-1 A WA 9/4/1989 Dos Palos Dos Palos,CA Gonzaga University - A 2011 2008-2011 Jones Austin Austin D. Jones Seattle,Washington 1-Jun 205 L R 1B 2011 June-Reg 7 239 20 New York Yankees 350000 1B H austin-jones-2 Rookie WA 8/20/1992 Edmonds-Woodway Edmonds,WA - - RK 2011 2011-2011 Carpenter Ryan Ryan Carpenter Peoria,Arizona 5-Jun 205 L L P 2011 June-Reg 7 240 28 Tampa -

2006 Topps Baseball Card Set Checklist
2006 TOPPS BASEBALL CARD SET CHECKLIST 1 Alex Rodriguez 2 Jose Valentin 3 Garrett Atkins 4 Scott Hatteberg 5 Carl Crawford 6 Armando Benitez 7 Mickey Mantle 8 Mike Morse 9 Damian Miller 10 Clint Barmes 11 Michael Barrett 12 Coco Crisp 13 Tadahito Iguchi 14 Chris Snyder 15 Brian Roberts 16 David Wright 17 Victor Santos 18 Trevor Hoffman 19 Jeremy Reed 20 Bobby Abreu 21 Lance Berkman 22 Zach Day 23 Jonny Gomes 24 Jason Marquis 25 Chipper Jones 26 Scott Hairston 27 Ryan Dempster 28 Brandon Inge 29 Aaron Harang 30 Jon Garland 31 Pokey Reese 32 Mike MacDougal 33 Mike Lieberthal 34 Cesar Izturis 35 Brad Wilkerson 36 Jeff Suppan 37 Adam Everett 38 Bengie Molina 39 Rickie Weeks 40 Jorge Posada 41 Rheal Cormier 42 Reed Johnson Compliments of BaseballCardBinders.com© 2019 1 43 Laynce Nix 44 Carl Everett 45 Greg Maddux 46 Jeff Francis 47 Felipe Lopez 48 Dan Johnson 49 Humberto Cota 50 Manny Ramirez 51 Juan Uribe 52 Jaret Wright 53 Tomo Ohka 54 Mike Matheny 55 Joe Mauer 56 Jarrod Washburn 57 Randy Winn 58 Pedro Feliz 59 Kenny Rogers 60 Rocco Baldelli 61 Eric Hinske 62 Damaso Marte 63 Desi Relaford 64 Juan Encarnacion 65 Nomar Garciaparra 66 Shawn Estes 67 Brian Jordan 68 Steve Kline 69 Braden Looper 70 Carlos Lee 71 Tom Glavine 72 Craig Biggio 73 Steve Finley 74 David Newhan 75 Eric Gagne 76 Tony Graffanino 77 Dallas McPherson 78 Nick Punto 79 Mark Kotsay 80 Kerry Wood 81 Kyle Farnsworth 82 Huston Street 83 Endy Chavez 84 So Taguchi 85 Hank Blalock 86 Brad Radke 87 Chien-Ming Wang 88 B.J. -

Coco Crisp 4
COCO CRISP 4 OUTFIELDER Height/Weight: 5-10 / 185 Bats/Throws: Switch / Right Birthdate: November 1, 1979 Opening Day Age: 36 Birthplace/Resides: Los Angeles, California / Rancho Mirage, California Major League Service: 12 years, 158 days Obtained: Re-signed as a free agent, January 5, 2012 Contract Status: Fifth year of a five-year contract through 2016 with a vesting option for 2017 CAREER HIGHLIGHTS Has played for four different teams in 14 Ma- jor League seasons…is a .268 career hitter with ATHLETICS CAREER STOLEN BASE Cleveland (2002-05), Boston (2006-08), Kansas PERCENTAGE LEADERS City (2009) and Oakland (2010-15)…has 299 ca- PLAYER SB SBA SB% reer stolen bases…has been successful in 162-of- 1. Coco Crisp (2010-15) 162 188 86.2% 188 (86.2%) stolen base attempts in an Oakland 2. Stan Javier (1986-95) 103 120 85.8% uniform, which is the best percentage in Athlet- 3. Rajai Davis (2008-10) 116 145 80.0% ics history…ranks fourth in Oakland history and 4. Rickey Henderson (1979-98) 867 1086 79.8% 10th in Athletics history in steals…has led off 5. Davey Lopes (1982-84) 62 78 79.5% the game with a home run 15 times in his career, Jose Tartabull (1962-70) 62 78 79.5% including 13 with the A’s, which is second most (min. 75 stolen base attempts) in Oakland history and tied for third in Athletics history behind Rickey Henderson (43) and Eddie Joost (19)…had career highs in home runs (22) and runs (93) with the A’s in 2013…tied for the Ameri- can League lead in stolen bases in 2011 (49) after topping the majors in stolen base percentage (91.4%) in 2010…stole 28 bases with Boston in 2007 to help the Red Sox to the World Championship and hit .281 (16 for 57) in 20 games over two postseasons with Boston (2007-08)…went 153 games and 429 total chances between errors from July 21, 2006 at Seattle to Aug. -
2012 Carolina League Media Guide
2012 Media Guide & Record Book CAROLINA LEAGUE OFFICE SALEM RED SOX ....................................36-39 General Information ......................... 2–3 WILMINGTON BLUE ROCKS....................40-43 Club Nicknames..................................... 4 WINSTON-SALEM DASH ............................44-47 Award Winners...................................... 5 2011 SEASON REVIEW SCHEDULES Summary ........................................48-49 Master League .................................. 6–7 Standings, Awards ................................50 Carolina Mudcats .................................. 8 Statistical Leaders ................................51 Frederick Keys ....................................... 9 Kinston Indians ....................................52 Lynchburg Hillcats ................................10 Complete Statistics .........................53-59 Myrtle Beach Pelicans ..........................11 LEAGUE RECORDS Potomac Nationals ...............................12 Individual Batting ...........................60-62 Salem Red Sox ......................................13 Single Season Performances .................63 Wilmington Blue Rocks .........................14 Yearly Batting Leaders ....................64-70 Winston-Salem Dash .............................15 Team Batting .................................71-72 TEAM INFORMATION ............................16-47 Individual Pitching ..........................73-74 Contact Information, Perfect Games, No-Hitters ...............75-76 Ownership, Management, Yearly Pitching -

2004 Media Guide
20042004 ALTOONA CURVE MEDIA GUIDE TABLE OF CONTENTS TEAM DIRECTORY....................................... 2 EXECUTIVE BIOS......................................... 3 BLAIR COUNTY BALLPARK......................... 4 TICKET INFORMATION.............................. 5 CURVE ATTENDANCE.............................. 6-7 GENERAL INFORMATION.......................... 8 2003 SEASON IN REVIEW......................... 9-15 Day-by-Day Results ............................. 10-12 Player Movement ................................. 13-14 Individual Statistics .................................. 15 Notebook............................................. 16-17 CURVE HISTORY AND RECORDS........ 19-32 Franchise History ................................ 20-21 All-Time Roster ........................................ 22 Curve to the Majors .................................. 23 Franchise Records ............................... 24-28 Single-Season Top Five Lists .................... 29 Career Top Five Lists ............................... 30 The 2004 Altoona Curve Media & Information Year-by-Year History ................................ 31 Guide is a publication of the Altoona Curve Media ............................................ 32 Relations Department. All information is current as Adam Hyzdu of March 24, 2004. THE EASTERN LEAGUE....................... 33-43 Eastern League Information ............... 34-35 This publication was designed, researched, written and ............... 36-37 edited by Jason Dambach, Curve Director of Media 2003 Eastern League Review -

2018 Media Guide.Indd
BUFFALO BISONS 2018 BUFFALO BISONS PLAYING SCHEDULE BUFFALO BISONS 2018 BUFFALO BISONS MEDIA GUIDE International League Governors’ Cup Champions 1933, 1936, 1957, 1961, 1998, 2004 International League North Division Champions 1998, 2000, 2001, 2004, 2005 American Association Champions 1997 COCA-COLA FIELD One James D. Griffi n Plaza THE TRIPLE-A Buff alo, NY 14203 bisons.com AFFILIATE OF THE (716) 846-2000 FAX (716) 852-6530 TABLE OF CONTENTS Bisons Front Offi ce 5 Final Bisons Statistics 61 Team Awards 94-95 Robert E. Rich Jr. 6 Bisons Team Leaders 62-63 Year-by-Year Records 96-97 Melinda R. Rich 8 Off ensive Breakdowns 64 Overall Team Records 98 Joseph W. Segarra 9 Home Runs 65 Playoff s 99 Jonathan A. Dandes 10 Pitching Breakdowns 66 Attendance 100 Mike Buczkowski 11 Defensive Breakdowns 67 Yearly Team Leaders 101-102 Kevin Parkinson 12 Transactions, Roster Details 68-69 Statistical Leaders 103-108 Robert Free 13 Season Highs & Lows 70 Playoff Leaders 109 Anthony Sprague 13 Team Records 110-112 Executive Biographies 14 2018 Opponents 71 Th e Last Time… 113-115 International League 72 All-Time Roster 116-126 2018 Bisons Coaching Staff 15 IL Ballparks 73 Managerial Roster 126 Bobby Meacham 16 IL Umpires 73 Managerial Leaders 126 Bob Stanley 17 Charlotte Knights 74 Modern Era Coaching Staff s 127 Corey Hart 18 Columbus Clippers 75 Devon White 18 Durham Bulls 76 Coca-Cola Field 128 Bob Tarpey 19 Gwinnett Stripers 77 Ballpark Vitals 129 Brian Pike 19 Indianapolis Indians 78 Ballpark Highlights 129-136 Medical Support Team 20-21 Lehigh Valley IronPigs 79 Ballpark Names 136 Louisville Bats 80 Bisons Statistics 137 2018 Bisons 22 Norfolk Tides 81 Home Openers 137 Bisons Players 23-53 Pawtucket Red Sox 82 Ballpark Records 138 Rochester Red Wings 83 Player Statistics 139-142 2017 Review 53 Scranton/Wilkes-Barre RailRiders 84 IL Standings 54 Syracuse Chiefs 85 Media Information 143 Home/Road Records 54 Toledo Mud Hens 86 Toronto Blue Jays 144 Records vs.