DOCSLIB.ORG

Initial Waves from Deformable Submarine Landslides

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Initial Waves from Deformable Submarine Landslides INITIAL WAVES FROM DEFORMABLE SUBMARINE LANDSLIDES A STUDY ON THE SEPARATION TIME AND PARAMETER RELATIONSHIPS A Thesis by JUSTIN ANDREW O'SHAY Submitted to the Office of Graduate Studies of Texas A&M University in partial fulfillment of the requirements for the degree of MASTER OF SCIENCE May 2012 Major Subject: Geophysics INITIAL WAVES FROM DEFORMABLE SUBMARINE LANDSLIDES A STUDY ON THE SEPARATION TIME AND PARAMETER RELATIONSHIPS A Thesis by JUSTIN ANDREW O'SHAY Submitted to the Office of Graduate Studies of Texas A&M University in partial fulfillment of the requirements for the degree of MASTER OF SCIENCE Approved by: Chair of Committee, Robert Weiss David Sparks Committee Members, James Kaihatu Head of Department, Rick Giardino May 2012 Major Subject: Geophysics iii ABSTRACT Initial Waves from Deformable Submarine Landslides A Study on the Separation Time and Parameter Relationships. (May 2012) Justin Andrew O'Shay, B.S., Texas A&M University Chair of Advisory Committee: Dr. Robert Weiss Dr. David Sparks Earthquake and submarine mass failure are the most frequent causes of tsunami waves. While the process of the tsunami generation by earthquakes is reasonably well understood, the generation of tsunami waves during submarine mass failure is not. Estimates of the energy released during a tsunamigenic earthquake and respec- tive tsunami wave draw a clear picture of the efficiency of the tsunami-generating process. However for submarine landslides, this is not as straightforward because the generation process has never been recorded in nature making energy inferences very difficult. Hence the efficiency of submarine landslide as tsunami generators is yet to be conclusively determined. As the result of this uncertainty, different equa- tions, derived from experimental data or theory, result in leading-wave amplitude that vary over 6 orders of magnitude for the same initial slide conditions. To arrive at more robust estimates of the leading-wave characteristics and associated runup, the spatiotemporal dynamics of the coupling between the slide body and water col- umn needs to be investigated. The duration the water surface deformation is coupled with the slide motion is an essential question to shed light on the energy transfer. A parametric study is conducted with the state-of-the-art hydrocode iSALE in order to shed light on this complex geophysical event. The mass, viscosity, and depth iv of submergence are the particular slide parameters varied and their relationship to runup and decoupling time is analyzed. v TABLE OF CONTENTS Page ABSTRACT :::::::::::::::::::::::::::::::::::: iii TABLE OF CONTENTS ::::::::::::::::::::::::::::: v LIST OF TABLES ::::::::::::::::::::::::::::::::: vii LIST OF FIGURES :::::::::::::::::::::::::::::::: viii 1. INTRODUCTION ::::::::::::::::::::::::::::::: 1 1.1 Introduction to tsunamis ::::::::::::::::::::::::: 1 1.2 Introduction to landslide-generated tsunamis :::::::::::::: 3 1.3 Research objectives :::::::::::::::::::::::::::: 8 1.3.1 Objectives ::::::::::::::::::::::::::::: 9 2. BACKGROUND ::::::::::::::::::::::::::::::: 10 2.1 Analytical theories and numerical approaches ::::::::::::: 10 2.2 Laboratory modeling approaches :::::::::::::::::::: 19 2.3 Evaluation of current approaches :::::::::::::::::::: 27 2.4 Hydrocode modeling ::::::::::::::::::::::::::: 28 2.4.1 Impact modeling ::::::::::::::::::::::::: 31 2.4.2 Landslide modeling :::::::::::::::::::::::: 31 2.4.3 iSALE validation ::::::::::::::::::::::::: 32 3. NUMERICAL EXPERIMENTS ::::::::::::::::::::::: 36 3.1 Grids and geometries ::::::::::::::::::::::::::: 36 3.2 Initial conditions ::::::::::::::::::::::::::::: 37 3.3 Data analysis ::::::::::::::::::::::::::::::: 39 3.3.1 Cavity dynamics analysis ::::::::::::::::::::: 41 3.3.2 Runup analysis :::::::::::::::::::::::::: 46 3.3.3 Modeling concerns :::::::::::::::::::::::: 47 4. RESULTS ::::::::::::::::::::::::::::::::::: 50 4.1 Cavity dynamics and separation time :::::::::::::::::: 50 4.2 Runup ::::::::::::::::::::::::::::::::::: 52 5. CONCLUSION :::::::::::::::::::::::::::::::: 55 5.1 Research impact :::::::::::::::::::::::::::::: 55 vi REFERENCES ::::::::::::::::::::::::::::::::::: 58 vii LIST OF TABLES TABLE Page 2.1 Masses used in experiments conducted by Liu et al. (2005). :::::::: 24 3.1 Table of variables used in numerical experiments. ::::::::::::: 37 3.2 Table of masses used in numerical simulations. ::::::::::::::: 38 3.3 List of depths of submergence −∆ used in numerical simulations. :::: 39 4.1 Table of r2 values for linear regression conducted on data collected from initial model runs. Calculations correspond to figure 4.1. ::::::::: 51 viii LIST OF FIGURES FIGURE Page 1.1 Estimated earthquake energy, EE, compared to the earthquakes generat- ing moment, M0. The circled dots are those nicknamed \tsunami earth- quakes" and can be determined by the two orders of magnitude energy deficiency between the projected ratio (Newman and Okal, 1998). :::: 5 1.2 ISSMGE Technical Committee on Landslides (TC-11) classification of submarine mass movements adapted by Locat and Lee (2002). :::::: 6 1.3 (a) Causes of submarine mass movements and factor of safety formula. (b) Schematic from Locat and Lee (2002) depicting the continuum of submarine mass movement events. ::::::::::::::::::::: 7 1.4 Pre-slide initial geometries for potential wave generation (Heller, 2008) : 8 2.1 Experimental set up for Wiegel (1955). ::::::::::::::::::: 10 2.2 Murty (1979) landslide variables sketch. :::::::::::::::::: 12 2.3 Landslide generated waves variables definition sketch (Synolakis, 2003). : 17 2.4 Photograph of Hammack's wave tank and piston generator (Hammack, 1973). ::::::::::::::::::::::::::::::::::::: 19 2.5 Comparison between Heinrich's numerical and experimental wave profiles for a submarine landslide placed 1cm below still water level. Times at t = 0:5s, t = 1:0s, t = 1:5sec : : : : : : : : : : : : : : : : : : : : : : : : : 21 2.6 Watt's schematic drawing of the experimental apparatus used in his sub- marine landslide study with a) top view b)side view (Watts, 1997) :::: 22 2.7 Water level time histories from Watts (1997) for a number of different masses. a) Shows near field water level history b) shows far field water level history. ::::::::::::::::::::::::::::::::: 23 2.8 Definition sketch for Liu et al. (2005) experiments. :::::::::::: 24 ix FIGURE Page 2.9 Photograph from Liu et al. (2005) large scale laboratory experiments. Notice the positive leading wave in front of the slide and the depression following from a series b experiment. :::::::::::::::::::: 25 2.10 Liu et al. (2005) graph of nondimensionalized run-up versus nondimen- sionalized depth of submergence. :::::::::::::::::::::: 26 2.11 Scaled initial wave height predictions (ordinate) for a given landslide and two different slide geometry scalings (abscissas); different symbols corre- spond to various empirical formula Weiss et al. (2011). :::::::::: 28 2.12 Gisler and Weaver (2006) schemtaic set up of the LaPalma landslide for two dimensional model runs conducted by SAGE. ::::::::::::: 32 2.13 A - Illustration of the Gilbert Inlet in Lituya Bay showing the rockslide, per Fritz et al. (2001). B - Simplified geometry as used in the laboratory experiments and the computions Weiss et al. (2009). ::::::::::: 33 2.14 (a-f) Snapshots illustrating the water motion associated with the maxima in the time series. (e) Comparison between the experimental data from Fritz et al. (2001) and model results computed with the iSALE model Weiss et al. (2009). :::::::::::::::::::::::::::::: 35 3.1 iSALE input file with respective variables labeled. ::::::::::::: 36 3.2 Snapshots illustrating slide motion at t = 0:0s to t = 2:50s, slope is in brown, slide blue and water in black. :::::::::::::::::::: 40 3.3 Cavity definition and evolution for a submarine landslide. The abscissa represents horizontal distance, x and the ordinate η is wave height. The 355kg slide with a submergence depth of −δ =1.935m was used to create these images. ::::::::::::::::::::::::::::::::: 41 (a) Cavity example for four different times. :::::::::::::: 41 (b) Cavity evolution from 0.0s to 0.70s. :::::::::::::::: 41 (c) Cavity decoupling stages :::::::::::::::::::::: 41 x FIGURE Page 3.4 The upper graph is an example of the area calculation and the lower is an example of the calculation of S for the 355.0 kg, −∆ =0.047m slide. : 44 3.5 Diagram of how κ the energy transfer parameter changes over the time during the coupling of the slide. From A to B the slide is fully coupled to the free surface and transferring the maximum amount of energy. From B to C represents stage 1 where the slide has undergone the initial decou- pling, C to D the second stage of decoupling has begun, D to E the third stage, and E to F the slide has decoupled from the free surface and the amount amount of conversion is going to zero. C would represent stage 1 decoupling, D stage 2 decoupling and E stage three decoupling. ::::: 45 3.6 Runup measurement example. :::::::::::::::::::::::: 46 (a) Runup calculation example. :::::::::::::::::::: 46 (b) Runup calculation exampled zoomed in. ::::::::::::: 46 3.7 Snapshots illustrating wave motion at t = 0:0s and t = 1:80s, slope is in brown, and water is in black. Notice the cell filled with water for the t = 1:80s snapshot. :::::::::::::::::::::::::::::: 47 3.8 Snapshots illustrating wave motion at t = 3:15s to t = 3:30s, slope is in brown, and water is in black. Notice the that the intersection of slope and water stays in the same grid cell for all times. ::::::::::::: 48 3.9 Snapshots illustrating
Load more

Recommended publications
  • Submarine Landslides in the Santa Barbara Channel As Potential Tsunami Sources H
    Submarine landslides in the Santa Barbara Channel as potential tsunami sources H. G. Greene, L. Y. Murai, P. Watts, N. A. Maher, M. A. Fisher, C. E. Paull, P. Eichhubl To cite this version: H. G. Greene, L. Y. Murai, P. Watts, N. A. Maher, M. A. Fisher, et al.. Submarine landslides in the Santa Barbara Channel as potential tsunami sources. Natural Hazards and Earth System Sciences, Copernicus Publ. / European Geosciences Union, 2006, 6 (1), pp.63-88. hal-00299251 HAL Id: hal-00299251 https://hal.archives-ouvertes.fr/hal-00299251 Submitted on 16 Jan 2006 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Natural Hazards and Earth System Sciences, 6, 63–88, 2006 SRef-ID: 1684-9981/nhess/2006-6-63 Natural Hazards European Geosciences Union and Earth © 2006 Author(s). This work is licensed System Sciences under a Creative Commons License. Submarine landslides in the Santa Barbara Channel as potential tsunami sources H. G. Greene1, L. Y. Murai2, P. Watts3, N. A. Maher4, M. A. Fisher5, C. E. Paull1, and P. Eichhubl6 1Monterey Bay Aquarium Research Institute (MBARI), 7700 Sandholdt Road, Moss Landing, CA 95039; Moss Landing Marine Laboratories, 8272 Moss Landing Road Moss Landing, CA 95039, USA 2Moss Landing Marine Laboratories, 8272 Moss Landing Road, Moss Landing, CA 95039, USA 3Applied Fluids Engineering, Inc., 5710 E.
    [Show full text]
  • Geotechnical and Geologic Constraints on Tsunamigenic Submarine Landslides
    GEOTECHNICAL AND GEOLOGIC CONSTRAINTS ON TSUNAMIGENIC SUBMARINE LANDSLIDES H.J. LEE U.S. Geological Survey, 345 Middlefield Road, Menlo Park, CA 94025 USA Abstract Modeling submarine-landslide-induced tsunamis requires many simplifications of the landslide process, although the real world is much more complicated. Clearly tsunami modelers cannot consider all facets, but there is value in being aware of the complications. This paper describes the many environments in which submarine landslides can occur and the triggers that typically initiate them. Earthquakes acting on continental or canyon slopes comprise probably the most common scenario but many other combinations of environments and triggers are possible. Surprisingly, many sediment-covered slopes in highly seismically active areas have not failed. A possible explanation for this phenomenon is a process called “seismic strengthening.” The existence of such a process reduces somewhat the risk of landslide tsunamis along active margins while maintaining the risk along passive margins. Once a trigger has initiated a landslide in one of the vulnerable environments, failed masses begin to move downslope. Depending upon initial density state, the masses may convert into fluid-like sediment flows or even more dilute turbidity currents. A model for quantifying the tendency to flow is provided. Finally, a case study of the landslides and landslide tsunamis that occurred in Port Valdez, Alaska, during the 1964 Great Alaska Earthquake is provided. The excellent data base, including before and after bathymetry, shows that both large rigid block motion and mobilized sediment flows can occur near each other during the same event. The intact blocks are more efficient in producing tsunamis but the sediment flow can move farther and can erode and entrain considerable bottom sediment as they progress across the seafloor.
    [Show full text]
  • Submarine Slope Stability
    Submarine Slope Stability Based on M.S. Engineering Thesis Development of a Database and Assessment of Seafloor Slope Stability Based on Published Literature By James Johnathan Hance, B. S. The University of Texas at Austin Supervisor Dr. Stephen G. Wright The University of Texas at Austin Project Report Prepared for the Minerals Management Service Under the MMS/OTRC Cooperative Research Agreement 1435-01-99-CA-31003 Task Order 18217 MMS Project 421 August 2003 OTRC Library Number: 8/03B121 For more information contact: Offshore Technology Research Center Texas A&M University 1200 Mariner Drive College Station, Texas 77845-3400 (979) 845-6000 or Offshore Technology Research Center The University of Texas at Austin 1 University Station C3700 Austin, Texas 78712-0318 (512) 471-6989 A National Science Foundation Graduated Engineering Research Center Submarine Slope Stability Executive Summary Background and Context Oil and gas developments often require placing equipment, e.g., subsea wells, pipelines and flowlines, foundation systems for floating structures, in areas with sloping seafloors. Submarine slope failures can occur in such areas and create soil slides. Thus the stability of submarine slopes must be considered in selecting the site for installing and designing seafloor equipment. Assessing submarine slope stability requires estimating the likelihood, extent, and impact of a slide during the lifetime of the facility. This assessment is difficult due to the large difference in time scales between the project life (10’s of years) and the geologic processes and triggering mechanisms that cause the slides (10,000’s of years) Such an assessment is best approached through a probabilistic risk analysis that considers the risks to the equipment; the causes, likelihood, and behavior of submarine slides; and the uncertainties.
    [Show full text]
  • Submarine Landslide Flows Simulation Through Centrifuge Modelling
    SUBMARINE LANDSLIDE FLOWS SIMULATION THROUGH CENTRIFUGE MODELLING by Chang Shin GUE A dissertation submitted for the degree of Doctor of Philosophy at the University of Cambridge Churchill College January 2012 “Do not go where the path may lead, go instead where there is no path and leave a trail” - Ralph Waldo Emerson “If I have seen further than others, it is by standing upon the shoulders of giants” - Isaac Newton “Continuous effort – not strength or intelligence – is the key to unlocking our potential” - Winston Churchill ABSTRACT SUBMARINE LANDSLIDE FLOWS SIMULATION THROUGH CENTRIFUGE MODELLING Chang Shin GUE Landslides occur both onshore and offshore. However, little attention has been given to offshore landslides (submarine landslides). Submarine landslides have significant impacts and consequences on offshore and coastal facilities. The unique characteristics of submarine landslides include large mass movements and long travel distances at very gentle slopes. This thesis is concerned with developing centrifuge scaling laws for submarine landslide flows through the study of modelling submarine landslide flows in a mini-drum centrifuge. A series of tests are conducted at different gravity fields in order to understand the scaling laws involved in the simulation of submarine landslide flows. The model slope is instrumented with miniature sensors for measurements of pore pressures at different locations beneath the landslide flow. A series of digital cameras are used to capture the landslide flow in flight. Numerical studies are also carried out in order to compare the results obtained with the data from the centrifuge tests. The Depth Averaged Material Point Method (DAMPM) is used in the numerical simulations to deal with large deformation (such as the long runout of submarine landslide flows).
    [Show full text]
  • Chapter 2 Spatial Patterns for Landslide Ecology Lawrence R
    University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln USDA National Wildlife Research Center - Staff U.S. Department of Agriculture: Animal and Plant Publications Health Inspection Service 2013 Chapter 2 Spatial patterns for Landslide Ecology Lawrence R. Walker University of Nevada, [email protected] Aaron B. Shiels USDA/APHIS/WS National Wildlife Research Center, [email protected] Follow this and additional works at: https://digitalcommons.unl.edu/icwdm_usdanwrc Part of the Life Sciences Commons Walker, Lawrence R. and Shiels, Aaron B., "Chapter 2 Spatial patterns for Landslide Ecology" (2013). USDA National Wildlife Research Center - Staff Publications. 1641. https://digitalcommons.unl.edu/icwdm_usdanwrc/1641 This Article is brought to you for free and open access by the U.S. Department of Agriculture: Animal and Plant Health Inspection Service at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in USDA National Wildlife Research Center - Staff ubP lications by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. Published in LANDSLIDE ECOLOGY (New York: Cambridge University Press, 2013), by Lawrence R. Walker (University of Nevada, Las Vegas) and Aaron B. Shiels (USDA National Wildlife Research Center, Hila, Hawai’i). This document is a U.S. government work, not subject to copyright in the United States. 2 Spatial patterns Key points 1. Remote sensing tools have greatly improved the mapping of both terrestrial and submarine landslides, particularly at global scales. At regional and local scales, environmental correlates are being found that help interpret spatial patterns and related ecological processes on landslides. 2. Landslides are frequent on only 4% of the terrestrial landscape and coverage varies over time because new landslides do not occur at a constant rate.
    [Show full text]
  • Wave-Induced Seafloor Instability in the Yellow River Delta
    Journal of Marine Science and Engineering Article Wave-Induced Seafloor Instability in the Yellow River Delta: Flume Experiments Xiuhai Wang 1,2,3, Chaoqi Zhu 1,2,3,4,* and Hongjun Liu 1,2,3,* 1 College of Environmental Science and Engineering, Ocean University of China, Qingdao 266000, China; [email protected] 2 Shandong Provincial Key Laboratory of Marine Environment and Geological Engineering, Qingdao 266000, China 3 Laboratory for Marine Geology, Qingdao National Laboratory for Marine Science and Technology, Qingdao 266000, China 4 Shandong Provincial Key Laboratory of Marine Ecology and Environment & Disaster Prevention and Mitigation, Qingdao 266000, China * Correspondence: [email protected] (C.Z.); [email protected] (H.L.) Received: 11 August 2019; Accepted: 1 October 2019; Published: 6 October 2019 Abstract: Geological disasters of seabed instability are widely distributed in the Yellow River Delta, posing a serious threat to the safety of offshore oil platforms and submarine pipelines. Waves act as one of the main factors causing the frequent occurrence of instabilities in the region. In order to explore the soil failure mode and the law for pore pressure response of the subaqueous Yellow River Delta under wave actions, in-lab flume tank experiments were conducted in this paper. In the experiments, wave loads were applied with a duration of 1 hour each day for 7 consecutive days; pore water pressure data of the soil under wave action were acquired, and penetration strength data of the sediments were determined after wave action. The results showed that the fine-grained seabed presented an arc-shaped oscillation failure form under wave action.
    [Show full text]
  • Detectability of Seismic Waves from the Submarine Landslide That Caused the 1998 Papua New Guinea Tsunami
    Detectability of seismic waves from the submarine landslide that caused the 1998 Papua New Guinea tsunami Akio Katsumata1, Yasuhiro Yoshida2, Kenji Nakata1, Kenichi Fujita1, Masayuki Tanaka1, Koji Tamaribuchi1, Takahito Nishimiya1, and Akio Kobayashi1 1Meteorological Research Institute, Japan Meteorological Agency, 1-1 Nagamine, Tsukuba, Ibaraki Prefecture, Japan 2Meteorological College, Japan Meteorological Agency, 7-4-81 Asahi-cho, Kashiwa, Chiba Prefecture, Japan Correspondence: Akio Katsumata ([email protected]) Abstract. On 17 July 1998, a tsunami caused serious damage on the northern coast of Papua New Guinea about 20 min after the mainshock of an Mw 7.0 earthquake. The tsunami has been attributed to a submarine landslide that occurred about 13 min after the mainshock because its arrival at the coast was too late and its height too great to be the direct result of the fault slip of the earthquake. Bathymetric data recorded after the tsunami revealed an amphitheater-like structure that was consistent with a 5 recent submarine landslide. Most current tsunami warning systems are based on analysis of the early arrivals of seismic waves generated by an earthquake. In this study we investigated whether evidence of the landslide could be identified in the coda waves recorded after the mainshock. Based on previous studies of the tsunami source, we constructed synthetic seismograms to represent the submarine landslide and compared them to the observed coda waves of the preceding earthquake, with particular attention to the period around 13 min after the mainshock ::in ::::::::frequency::::::ranges::::close::to:::the::::::::landslide:::::::duration. We found phases 10 possibly corresponding to the landslide event.
    [Show full text]
  • Goals, Strategies, Priorities and Tasks
    GOALS, STRATEGIES, PRIORITIES AND TASKS OF A NATIONAL LANDSLIDE HAZARD-REDUCTION PROGRAM By U.S. Geological Survey U.S. Geological Survey Open-file Report 81-987 This report is preliminary and has not been edited or reviewed for conformity with Geological Survey editorial standards and nomenclature CONTENTS Page Preface ............................................................. 1 Introduction •••••••••••••••••••••••••••••••••••••••••••••••••••••••••• 3 Proposed National Program for Ground Failure Research ••••••••••••••••• 4 Role of the U.S. Geological Survey •••••••••••••••••••••••••••••••• 4 Goals of a National Program ••••••••••••••••••••••••••••••••••••••• 4 Strategies for U.S. Geological Survey Participation •••••••••••••• 4 De fini tions ••••••••••••••••••••••••••••••••••••••••••••••••••••••••••• 5 Goals for Landslide Hazard Mapping and Risk Evaluation •••••••••••••••• 6 Strategies for Mapping Hazards on Natural Slopes •••••••••••••••••• 1 Reconnaissance Approach--Simple Inventories •••••••••••••••••• 1 Intermediate Types of Landslide Inventories •••••••••••••••••• 9 Detailed Inventories ••••••••••••••••••••••••••••••••••••••••• 10 Terrain Analyses ••••••••••••••••••••••••••••••••••••••••••••• 12 Slope Stability Maps ••••••••••••••••••••••••••••••••••••••••• 14 Landslide Hazard Maps •••••••••••••••••••••••••••••••••••••••• 14 Risk Maps •••••••••••••••••••••••••••••••••••••••••••••••••••• 20 La nd -U se Maps •••••••••••••••••••••••••••••••••••••••••••••••• 20 Map Scales .................................................. 20 Present
    [Show full text]
  • Tsuinfo Alert, June 2008
    Contents Volume 10, Number 3 June 2008 ______________________________________________________________________________________________________________________________ Special features Departments Giant wave in Lituya Bay (50th anniversary) 1 Hazard mitigation news 15 Changing roles & responsibilities of the local emergency manager 4 Websites 17 Shadowed by the glare of 1906 are faceless future dangers 12 Publications 18 Warnings on the horizon—Air patrol pilots 13 Conferences/seminars/symposium 19 Airborne tsunami alert triggers wave of text messaging 14 Classes 19 Insights into the problems of communicating tsunami warnings 14 Media 19 Un-natural disasters 20 State Emergency Management offices 21 Rural students build model tsunami shelters 26 Material added to NTHMP Library 21 Detecting tsunami genesis 11 IAQ 28 Video reservations 27 ____________________________________________________________________________________________________ 50th ANNIVERSARY OF LITUYA BAY TSUNAMI, July 9, 1958 The Alaska Earthquake of July 10, 1958*: Giant wave in Lituya Bay By Don J. Miller Bulletin of the Seismological Society of America, v. 50, no. 2, excerpts p.257-259. Map: U.S. Geological Survey Professional Paper 354-C Continued on page 3 TsuInfo Alert is prepared by the Washington State Department of Natural Resources on behalf of the National Tsunami Hazard Mitigation Program, a State/Federal Partnership funded through the National Oceanic and Atmospheric Administration (NOAA). It is assembled by Lee Walkling, Librarian, and is published bi-monthly by
    [Show full text]
  • Advances in the Study of Mega-Tsunamis in the Geological Record Raphael Paris, Kazuhisa Goto, James Goff, Hideaki Yanagisawa
    Advances in the study of mega-tsunamis in the geological record Raphael Paris, Kazuhisa Goto, James Goff, Hideaki Yanagisawa To cite this version: Raphael Paris, Kazuhisa Goto, James Goff, Hideaki Yanagisawa. Advances in the study of mega-tsunamis in the geological record. Earth-Science Reviews, Elsevier, 2020, 210, pp.103381. 10.1016/j.earscirev.2020.103381. hal-02964184 HAL Id: hal-02964184 https://hal.uca.fr/hal-02964184 Submitted on 12 Nov 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. 1 Advances in the study of mega-tsunamis in the geological record 2 3 Raphaël Paris1, Kazuhisa Goto2, James Goff3, Hideaki Yanagisawa4 4 1 Université Clermont Auvergne, CNRS, IRD, OPGC, Laboratoire Magmas et Volcans, F-63000 Clermont- 5 Ferrand, France. 6 2 Department of Earth and Planetary Science, The University of Tokyo, Hongo 7-3-1, Tokyo, Japan. 7 3 PANGEA Research Centre, UNSW Sydney, Sydney, NSW 2052, Australia. 8 4 Department of Regional Management, Tohoku Gakuin University, Tenjinsawa 2‑ 1‑ 1, Sendai, Japan. 9 10 Abstract 11 Extreme geophysical events such as asteroid impacts and giant landslides can generate mega- 12 tsunamis with wave heights considerably higher than those observed for other forms of 13 tsunamis.
    [Show full text]
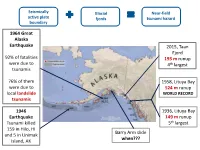
  • Alaska Tsunami Hazard Maps and Modeling Slides
    Seismically Glacial Near-field active plate fjords tsunami hazard boundary 1964 Great Alaska Earthquake 2015, Taan Fjord 92% of fatalities 193 m runup were due to 4th largest tsunamis 76% of them 1958, Lituya Bay were due to 524 m runup local landslide WORLD RECORD tsunamis 1946 1936, Lituya Bay Earthquake 149 m runup Tsunami killed 5th largest 159 in Hilo, HI Barry Arm slide and 5 in Unimak Island, AK when??? History of the product line: 1998 - 2021 High-resolution maps and reports 2018 Update 1998 Regional maps 2014 Maritime 2016 Pedestrian Subsidence Brochures 2020 FY 2019-2020 project areas A l a s k a Bering Sea Seward Bristol Bay Kodiak Is. Gulf of Alaska Regional tsunami hazard assessment: Bristol Bay Bristol Bay Tectonic and landslide tsunami sources Maximum tsunami energy Tectonic tsunamis Landslide tsunamis Tsunami hazard is higher than expected Nelson Lagoon Platinum High-resolution modeling: Kodiak villages • Regional tsunami hazard assessment was completed in 2018 • In FY2019-2020 project period, we performed high- resolution modeling and mapping for 7 Kodiak communities. From regional assessment to high-resolution maps Regional tsunami hazard High-resolution tsunami assessment inundation map Visiting Kodiak communities New tsunami shelter in Chiniak New tsunami shelter in Ouzinkie Updating tsunami hazard map of Seward 1964 inundation • The previous report was published before Old report the 2011 Tohoku tsunami. New sources • We made a new set of potential tsunami sources that include large amount of slip in the shallow part of the megathrust, similar to that in the Tohoku earthquake. • We also consider splay faults that have been mapped offshore Kenai Peninsula.
    [Show full text]
  • Topographic Characteristics of the Submarine Taiwan Orogen L
    JOURNAL OF GEOPHYSICAL RESEARCH, VOL. 111, F02009, doi:10.1029/2005JF000314, 2006 Topographic characteristics of the submarine Taiwan orogen L. A. Ramsey,1 N. Hovius,2 D. Lague,3 and C.-S. Liu4 Received 21 March 2005; revised 15 December 2005; accepted 6 January 2006; published 18 May 2006. [1] A complete digital elevation and bathymetry model of Taiwan provides the opportunity to characterize the topography of an emerging mountain belt. The orogen appears to form a continuous wedge of constant slope extending from the subaerial peaks to the submarine basin. We compare submarine channel systems from the east coast of Taiwan with their subaerial counterparts and document a number of fundamental similarities between the two environments. The submarine channel systems form a dendritic network with distinct hillslopes and channels. There is minimal sediment input from the subaerial landscape and sea level changes are insignificant, suggesting that the submarine topography is sculpted by offshore processes alone. We implement a range of geomorphic criteria, widely applied to subaerial digital elevation models, and explore the erosional processes responsible for sculpting the submarine and subaerial environments. The headwaters of the submarine channels have steep, straight slopes and a low slope-area scaling exponent, reminiscent of subaerial headwaters that are dominated by bedrock landslides. The main trunk streams offshore have concave-up longitudinal profiles, extensive knickpoints, and a slope-area scaling exponent similar in form to the onshore fluvial domain. We compare the driving mechanisms of the likely offshore erosional processes, primarily debris flows and turbidity currents, with subaerial fluvial incision. The results have important implications for reading the geomorphic signals of the submarine and subaerial landscapes, for understanding the links between the onshore and offshore environments, and, more widely, for focusing the future research of the submarine slope.
    [Show full text]