DOCSLIB.ORG

Geometry: Shapes and Their Attributes

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Geometry: Shapes and Their Attributes © http://www.teacherspayteachers.com/Store/Cassie-Smith Geometry: Shapes and Their Attributes Aligned to CCSS 3.G.1 What You Get: • Quadrilateral “Club” Poster • Quadrilateral “Club” Cloze Note Taker (perfect for Math Notebooks) • Student Activity Pages (3) - Students draw quadrilaterals and non-quadrilaterals using the “Club” Poster and/or Note Taker. • The Geometry Family Tree (“GeomeTree”)- Students fill in the tree and draw each shape with its correct attributes. • Sort Activity- Students sort shapes based on attributes using their GeomeTrees or “Club” Note Takers. • “Describe Figures” Worksheet- Students describe figures using vocabulary from a provided word bank. • Classifying Polygons and Their Attributes Checklist • Teacher Keys Enjoy and please leave feedback! © http://www.teacherspayteachers.com/Store/Cassie-Smith All Parallelograms are Quadrangles/Quadrilaterals (4 angles and 4 sides) Parallelogram “Club” Rule: Must have 2 pairs of parallel sides Rhombus “Club” Rule: Must have 4 equal sides Rectangle “Club” Square “Club”* Rule: Must have 4 right angles (90º) *Square gets into all 3 clubs: Parallelogram, Rhombus, and Rectangle Clubs! Name: All Parallelograms are Quadrangles/Quadrilaterals ( angles and sides) “Club” Rule: Must have pairs of “Club” sides Rule: Must have 4 “Club” “Club”* Rule: Must have 4 * gets into all 3 clubs: Parallelogram, Rhombus, and Rectangle Clubs! Name: Geometry Use the Quadrilateral Diagram to complete. Draw 2 different polygons that would belong in Draw 2 different Quadrilaterals: the Parallelogram “Club”: Geometry P. 2 Use the Quadrilateral Diagram to complete. Draw 2 different polygons that would belong in Draw 2 different polygons that would belong in the Rectangle “Club”: the Rhombus “Club”: Geometry P. 3 Use the Quadrilateral Diagram to complete. Draw 2 different polygons that would belong in Draw 2 different Quadrilaterals that would not the Square “Club”: fit into any of the clubs: The Geometry Family Name “GeomeTree” The Geometry Family Name “GeomeTree” Polygons Quadrilaterals Parallelograms Non-Parallelograms Trapezoids Kites Others Rhombi Rectangles Squares Sort Directions: Cut apart and sort by stacking like polygons on the branches of your “GeomeTree”. Name: Describe Figures Use as many words below as possible to describe each figure. quadrilateral parallelogram rectangle square polygon 1. 2. 3. 4. Name: Describe Figures Use as many words below as possible to describe each figure. quadrilateral parallelogram rectangle square polygon polygon, quadrilateral, 1. parallelogram, rectangle 2. polygon, quadrilateral, parallelogram, rectangle, square polygon, quadrilateral, 3. parallelogram polygon, quadrilateral 4. Name: Classifying Polygons by Their Attributes Put an X for the attribute(s) that is/are true for each polygon. Both pairs of Both pairs of opposite sides are opposite sides are Four square All sides are the Polygon 4 sides parallel the same length corners same length Quadrilateral Parallelogram Rhombus Rectangle Square Credits Fonts by: Christina Bainbridge Graphics and Borders by: From the Pond, LoveTwoTeach and Creative Clips Idea inspired by: http://www.alyciazimmerman.com/math-charts.html Thanks for your purchase! Please leave feedback! Remember each time you leave feedback you receive TpT credits that work like $$ towards future purchases. ~Cassie © http://www.teacherspayteachers.com/Store/Cassie-Smith .
Load more

Recommended publications
  • How Can You Put Shapes Together to Make Other Shapes?
    Lesson 27 Understand Tiling in Rectangles Name: How can you put shapes together to make other shapes? Study the example showing how to put shapes together to make other shapes. Then solve Problems 1–4. Example How can you use smaller shapes to make a circle? Look at the shapes in the green box Draw lines to show how you could use the shapes Write how many of each shape you would need 2 4 1 Draw a line to show how you could use squares like the one in the green box to make a rectangle How many squares would you need? squares 2 Draw lines to show how you could use triangles like the one in the green box to make a rectangle How many triangles would you need? triangles ©Curriculum Associates, LLC Copying is not permitted. Lesson 27 Understand Tiling in Rectangles 283 Solve. 3 Draw lines to show how you could use hexagons to make the first shape below Then show how you could use trapezoids to make the second shape How many of each shape would you need? hexagons trapezoids 4 Draw lines to show how you could use triangles to make the first shape below Then show how you could use trapezoids to make the second shape Then show how you could use rhombuses to make the third shape How many of each shape would you need? triangles trapezoids rhombuses 284 Lesson 27 Understand Tiling in Rectangles ©Curriculum Associates, LLC Copying is not permitted. Lesson 27 Name: Draw and Count Squares Study the example showing how to draw and count squares.
    [Show full text]
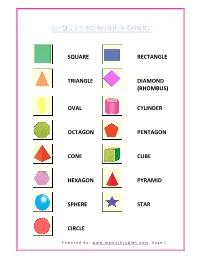
  • Square Rectangle Triangle Diamond (Rhombus) Oval Cylinder Octagon Pentagon Cone Cube Hexagon Pyramid Sphere Star Circle
    SQUARE RECTANGLE TRIANGLE DIAMOND (RHOMBUS) OVAL CYLINDER OCTAGON PENTAGON CONE CUBE HEXAGON PYRAMID SPHERE STAR CIRCLE Powered by: www.mymathtables.com Page 1 what is Rectangle? • A rectangle is a four-sided flat shape where every angle is a right angle (90°). means "right angle" and show equal sides. what is Triangle? • A triangle is a polygon with three edges and three vertices. what is Octagon? • An octagon (eight angles) is an eight-sided polygon or eight-gon. what is Hexagon? • a hexagon is a six-sided polygon or six-gon. The total of the internal angles of any hexagon is 720°. what is Pentagon? • a plane figure with five straight sides and five angles. what is Square? • a plane figure with four equal straight sides and four right angles. • every angle is a right angle (90°) means "right ang le" show equal sides. what is Rhombus? • is a flat shape with four equal straight sides. A rhombus looks like a diamond. All sides have equal length. Opposite sides are parallel, and opposite angles are equal what is Oval? • Many distinct curves are commonly called ovals or are said to have an "oval shape". • Generally, to be called an oval, a plane curve should resemble the outline of an egg or an ellipse. Powered by: www.mymathtables.com Page 2 What is Cube? • Six equal square faces.tweleve edges and eight vertices • the angle between two adjacent faces is ninety. what is Sphere? • no faces,sides,vertices • All points are located at the same distance from the center. what is Cylinder? • two circular faces that are congruent and parallel • faces connected by a curved surface.
    [Show full text]
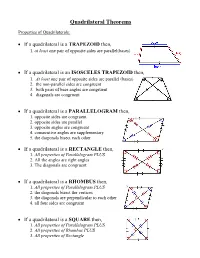
  • Quadrilateral Theorems
    Quadrilateral Theorems Properties of Quadrilaterals: If a quadrilateral is a TRAPEZOID then, 1. at least one pair of opposite sides are parallel(bases) If a quadrilateral is an ISOSCELES TRAPEZOID then, 1. At least one pair of opposite sides are parallel (bases) 2. the non-parallel sides are congruent 3. both pairs of base angles are congruent 4. diagonals are congruent If a quadrilateral is a PARALLELOGRAM then, 1. opposite sides are congruent 2. opposite sides are parallel 3. opposite angles are congruent 4. consecutive angles are supplementary 5. the diagonals bisect each other If a quadrilateral is a RECTANGLE then, 1. All properties of Parallelogram PLUS 2. All the angles are right angles 3. The diagonals are congruent If a quadrilateral is a RHOMBUS then, 1. All properties of Parallelogram PLUS 2. the diagonals bisect the vertices 3. the diagonals are perpendicular to each other 4. all four sides are congruent If a quadrilateral is a SQUARE then, 1. All properties of Parallelogram PLUS 2. All properties of Rhombus PLUS 3. All properties of Rectangle Proving a Trapezoid: If a QUADRILATERAL has at least one pair of parallel sides, then it is a trapezoid. Proving an Isosceles Trapezoid: 1st prove it’s a TRAPEZOID If a TRAPEZOID has ____(insert choice from below) ______then it is an isosceles trapezoid. 1. congruent non-parallel sides 2. congruent diagonals 3. congruent base angles Proving a Parallelogram: If a quadrilateral has ____(insert choice from below) ______then it is a parallelogram. 1. both pairs of opposite sides parallel 2. both pairs of opposite sides ≅ 3.
    [Show full text]
  • Cyclic Quadrilateral: Cyclic Quadrilateral Theorem and Properties of Cyclic Quadrilateral Theorem (For CBSE, ICSE, IAS, NET, NRA 2022)
    9/22/2021 Cyclic Quadrilateral: Cyclic Quadrilateral Theorem and Properties of Cyclic Quadrilateral Theorem- FlexiPrep FlexiPrep Cyclic Quadrilateral: Cyclic Quadrilateral Theorem and Properties of Cyclic Quadrilateral Theorem (For CBSE, ICSE, IAS, NET, NRA 2022) Get unlimited access to the best preparation resource for competitive exams : get questions, notes, tests, video lectures and more- for all subjects of your exam. A quadrilateral is a 4-sided polygon bounded by 4 finite line segments. The word ‘quadrilateral’ is composed of two Latin words, Quadric meaning ‘four’ and latus meaning ‘side’ . It is a two-dimensional figure having four sides (or edges) and four vertices. A circle is the locus of all points in a plane which are equidistant from a fixed point. If all the four vertices of a quadrilateral ABCD lie on the circumference of the circle, then ABCD is a cyclic quadrilateral. In other words, if any four points on the circumference of a circle are joined, they form vertices of a cyclic quadrilateral. It can be visualized as a quadrilateral which is inscribed in a circle, i.e.. all four vertices of the quadrilateral lie on the circumference of the circle. What is a Cyclic Quadrilateral? In the figure given below, the quadrilateral ABCD is cyclic. ©FlexiPrep. Report ©violations ＠https://tips.fbi.gov/ 1 of 5 9/22/2021 Cyclic Quadrilateral: Cyclic Quadrilateral Theorem and Properties of Cyclic Quadrilateral Theorem- FlexiPrep Let us do an activity. Take a circle and choose any 4 points on the circumference of the circle. Join these points to form a quadrilateral. Now measure the angles formed at the vertices of the cyclic quadrilateral.
    [Show full text]
  • Properties of Equidiagonal Quadrilaterals (2014)
    Forum Geometricorum Volume 14 (2014) 129–144. FORUM GEOM ISSN 1534-1178 Properties of Equidiagonal Quadrilaterals Martin Josefsson Abstract. We prove eight necessary and sufficient conditions for a convex quadri- lateral to have congruent diagonals, and one dual connection between equidiag- onal and orthodiagonal quadrilaterals. Quadrilaterals with both congruent and perpendicular diagonals are also discussed, including a proposal for what they may be called and how to calculate their area in several ways. Finally we derive a cubic equation for calculating the lengths of the congruent diagonals. 1. Introduction One class of quadrilaterals that have received little interest in the geometrical literature are the equidiagonal quadrilaterals. They are defined to be quadrilat- erals with congruent diagonals. Three well known special cases of them are the isosceles trapezoid, the rectangle and the square, but there are other as well. Fur- thermore, there exists many equidiagonal quadrilaterals that besides congruent di- agonals have no special properties. Take any convex quadrilateral ABCD and move the vertex D along the line BD into a position D such that AC = BD. Then ABCD is an equidiagonal quadrilateral (see Figure 1). C D D A B Figure 1. An equidiagonal quadrilateral ABCD Before we begin to study equidiagonal quadrilaterals, let us define our notations. In a convex quadrilateral ABCD, the sides are labeled a = AB, b = BC, c = CD and d = DA, and the diagonals are p = AC and q = BD. We use θ for the angle between the diagonals. The line segments connecting the midpoints of opposite sides of a quadrilateral are called the bimedians and are denoted m and n, where m connects the midpoints of the sides a and c.
    [Show full text]
  • Teach the Square…And the Rectangle
    f e a t u r e Teach the square…and the rectangle eaching these two geometric needs of ancient civilizations. familiar and trusted shapes, they Tshapes is like a line from an (Some believe the square symbol- represent order and stability. old song: “You can’t have one izes civilization.) Ancient peoples Because a square has four equal without the other.” needed to measure plots of land, sides, it can also be said to sym- The square and rectangle go build structures, collect taxes, bolize the seasons (spring, sum- hand in hand—maybe not like describe constellations, and create mer, fall, winter), cardinal direc- “love and marriage” or “horse calendars, all of which required tions (north, east, south, west), and carriage,” but perhaps best numbers, shapes, and calculations. and the elements (fire, water, air, understood in terms of the other. Of the basic geometric shapes in earth). Children have undoubtedly had today’s world, the rectangle is the In nature, we see no naturally experience with the two shapes in most common. The rectangle and formed squares or rectangles. objects all around them. They its square soul-mate form the Trees, branches, and leaves, for begin learning geometric shapes structure of most buildings. As example, are uneven, rounded, in a more formal way in preschool z T and are usually expected to know gae how to make and take apart N shapes by the time they finish kindergarten. by susa oto Texas Child Care has posted two ph previous articles on teaching geo- metric shapes: Go round: Teach the circle shape in Spring 2015 and Teach the triangle in Spring 2017.
    [Show full text]
  • Petrie Schemes
    Canad. J. Math. Vol. 57 (4), 2005 pp. 844–870 Petrie Schemes Gordon Williams Abstract. Petrie polygons, especially as they arise in the study of regular polytopes and Coxeter groups, have been studied by geometers and group theorists since the early part of the twentieth century. An open question is the determination of which polyhedra possess Petrie polygons that are simple closed curves. The current work explores combinatorial structures in abstract polytopes, called Petrie schemes, that generalize the notion of a Petrie polygon. It is established that all of the regular convex polytopes and honeycombs in Euclidean spaces, as well as all of the Grunbaum–Dress¨ polyhedra, pos- sess Petrie schemes that are not self-intersecting and thus have Petrie polygons that are simple closed curves. Partial results are obtained for several other classes of less symmetric polytopes. 1 Introduction Historically, polyhedra have been conceived of either as closed surfaces (usually topo- logical spheres) made up of planar polygons joined edge to edge or as solids enclosed by such a surface. In recent times, mathematicians have considered polyhedra to be convex polytopes, simplicial spheres, or combinatorial structures such as abstract polytopes or incidence complexes. A Petrie polygon of a polyhedron is a sequence of edges of the polyhedron where any two consecutive elements of the sequence have a vertex and face in common, but no three consecutive edges share a commonface. For the regular polyhedra, the Petrie polygons form the equatorial skew polygons. Petrie polygons may be defined analogously for polytopes as well. Petrie polygons have been very useful in the study of polyhedra and polytopes, especially regular polytopes.
    [Show full text]
  • Quadrilaterals
    Name: Quadrilaterals Match the quadrilateral with its definition. a. 1. All sides are the same length. There are four right angles. Parallelogram b. 2. There is only one pair of parallel sides. Rectangle c. 3. Opposite sides are parallel and the same length. There are four right angles. Trapezoid d. 4. There are two pairs of parallel sides. All sides are the same length. Rhombus 5. There are two pairs of opposite parallel e. sides. Square 6. List two ways a rectangle and square are alike and one way in which they are different. Super Teacher Worksheets - www.superteacherworksheets.com ANSWER KEY Quadrilaterals Match the quadrilateral with its definition. a. e 1. All sides are the same length. There are four right angles. Parallelogram b. c 2. There is only one pair of parallel sides. Rectangle c. b 3. Opposite sides are parallel and the same length. There are four right angles. Trapezoid d. d 4. There are two pairs of parallel sides. All sides are the same length. Rhombus a 5. There are two pairs of opposite parallel e. sides. Square 6. List two ways a rectangle and square are alike and one way in which they are different. Rectangles and squares are alike in that both have two pairs of parallel sides and four right angles. They are different because a square must have four equal sides lengths and a rectangle has two pairs of equal side lengths. Super Teacher Worksheets - www.superteacherworksheets.com.
    [Show full text]
  • Cyclic Quadrilaterals — the Big Picture Yufei Zhao [email protected]
    Winter Camp 2009 Cyclic Quadrilaterals Yufei Zhao Cyclic Quadrilaterals | The Big Picture Yufei Zhao [email protected] An important skill of an olympiad geometer is being able to recognize known configurations. Indeed, many geometry problems are built on a few common themes. In this lecture, we will explore one such configuration. 1 What Do These Problems Have in Common? 1. (IMO 1985) A circle with center O passes through the vertices A and C of triangle ABC and intersects segments AB and BC again at distinct points K and N, respectively. The circumcircles of triangles ABC and KBN intersects at exactly two distinct points B and M. ◦ Prove that \OMB = 90 . B M N K O A C 2. (Russia 1995; Romanian TST 1996; Iran 1997) Consider a circle with diameter AB and center O, and let C and D be two points on this circle. The line CD meets the line AB at a point M satisfying MB < MA and MD < MC. Let K be the point of intersection (different from ◦ O) of the circumcircles of triangles AOC and DOB. Show that \MKO = 90 . C D K M A O B 3. (USA TST 2007) Triangle ABC is inscribed in circle !. The tangent lines to ! at B and C meet at T . Point S lies on ray BC such that AS ? AT . Points B1 and C1 lies on ray ST (with C1 in between B1 and S) such that B1T = BT = C1T . Prove that triangles ABC and AB1C1 are similar to each other. 1 Winter Camp 2009 Cyclic Quadrilaterals Yufei Zhao A B S C C1 B1 T Although these geometric configurations may seem very different at first sight, they are actually very related.
    [Show full text]
  • Cyclic Quadrilaterals
    GI_PAGES19-42 3/13/03 7:02 PM Page 1 Cyclic Quadrilaterals Definition: Cyclic quadrilateral—a quadrilateral inscribed in a circle (Figure 1). Construct and Investigate: 1. Construct a circle on the Voyage™ 200 with Cabri screen, and label its center O. Using the Polygon tool, construct quadrilateral ABCD where A, B, C, and D are on circle O. By the definition given Figure 1 above, ABCD is a cyclic quadrilateral (Figure 1). Cyclic quadrilaterals have many interesting and surprising properties. Use the Voyage 200 with Cabri tools to investigate the properties of cyclic quadrilateral ABCD. See whether you can discover several relationships that appear to be true regardless of the size of the circle or the location of A, B, C, and D on the circle. 2. Measure the lengths of the sides and diagonals of quadrilateral ABCD. See whether you can discover a relationship that is always true of these six measurements for all cyclic quadrilaterals. This relationship has been known for 1800 years and is called Ptolemy’s Theorem after Alexandrian mathematician Claudius Ptolemaeus (A.D. 85 to 165). 3. Determine which quadrilaterals from the quadrilateral hierarchy can be cyclic quadrilaterals (Figure 2). 4. Over 1300 years ago, the Hindu mathematician Brahmagupta discovered that the area of a cyclic Figure 2 quadrilateral can be determined by the formula: A = (s – a)(s – b)(s – c)(s – d) where a, b, c, and d are the lengths of the sides of the a + b + c + d quadrilateral and s is the semiperimeter given by s = 2 . Using cyclic quadrilaterals, verify these relationships.
    [Show full text]
  • Rectangles with the Same Numerical Area and Perimeter
    Rectangles with the Same Numerical Area and Perimeter About Illustrations: Illustrations of the Standards for Mathematical Practice (SMP) consist of several pieces, including a mathematics task, student dialogue, mathematical overview, teacher reflection questions, and student materials. While the primary use of Illustrations is for teacher learning about the SMP, some components may be used in the classroom with students. These include the mathematics task, student dialogue, and student materials. For additional Illustrations or to learn about a professional development curriculum centered around the use of Illustrations, please visit mathpractices.edc.org. About the Rectangles with the Same Numerical Area and Perimeter Illustration: This Illustration’s student dialogue shows the conversation among three students who are trying to find all rectangles that have the same numerical area and perimeter. After trying different rectangles of specific dimensions, students finally develop an equation that describes the relationship between the width and length of a rectangle with equal area and perimeter. Highlighted Standard(s) for Mathematical Practice (MP) MP 1: Make sense of problems and persevere in solving them. MP 2: Reason abstractly and quantitatively. MP 7: Look for and make use of structure. MP 8: Look for and express regularity in repeated reasoning. Target Grade Level: Grades 8–9 Target Content Domain: Creating Equations (Algebra Conceptual Category) Highlighted Standard(s) for Mathematical Content A.CED.A.2 Create equations in two or more variables to represent relationships between quantities; graph equations on coordinate axes with labels and scales. A.CED.A.4 Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations.
    [Show full text]
  • 2 Dimensional Figures
    Study Island Copyright © 2021 Edmentum - All rights reserved. Generation Date: 07/26/2021 Generated By: Jennifer Fleming 1. An equilateral triangle is always an example of a/an: I. isosceles triangle II. scalene triangle III. right triangle A. I only B. II and III C. I and II D. II only 2. Which of the following is true about a parallelogram? Parallelograms always have four congruent sides. A. The diagonals of a parallelogram always bisect each other. B. Only two sides of a parallelogram are parallel. C. Opposite angles of a parallelogram are not congruent. D. 3. What is the difference between a rectangle and a rhombus? A rectangle has opposite sides parallel and a rhombus has no sides parallel. A. A rectangle has four right angles and a rhombus has opposite angles of equal measure. B. A rhombus has four right angles and a rectangle has opposite angles of equal measure. C. A rectangle has opposite sides of equal measure and a rhombus has no sides of equal measure. D. 4. What is a property of all rectangles? The four sides of a rectangle have equal length. A. The opposite sides of a rectangle are parallel. B. The diagonals of a rectangle do not have equal length. C. A rectangle only has two right angles. D. 5. An obtuse triangle is sometimes an example of a/an: I. scalene triangle II. isosceles triangle III. equilateral triangle IV. right triangle A. I or II B. I, II, or III C. III or IV D. II or III 6. What is the main difference between squares and rhombuses? Squares always have four interior angles which each measure 90°; rhombuses do not.
    [Show full text]