Centipede Game Here Is the Extensive Game We Discussed in Class: Player 1 Moves First, and Can End the Game by Choosing L. Alter
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Game Theory 2: Extensive-Form Games and Subgame Perfection
Game Theory 2: Extensive-Form Games and Subgame Perfection 1 / 26 Dynamics in Games How should we think of strategic interactions that occur in sequence? Who moves when? And what can they do at different points in time? How do people react to different histories? 2 / 26 Modeling Games with Dynamics Players Player function I Who moves when Terminal histories I Possible paths through the game Preferences over terminal histories 3 / 26 Strategies A strategy is a complete contingent plan Player i's strategy specifies her action choice at each point at which she could be called on to make a choice 4 / 26 An Example: International Crises Two countries (A and B) are competing over a piece of land that B occupies Country A decides whether to make a demand If Country A makes a demand, B can either acquiesce or fight a war If A does not make a demand, B keeps land (game ends) A's best outcome is Demand followed by Acquiesce, worst outcome is Demand and War B's best outcome is No Demand and worst outcome is Demand and War 5 / 26 An Example: International Crises A can choose: Demand (D) or No Demand (ND) B can choose: Fight a war (W ) or Acquiesce (A) Preferences uA(D; A) = 3 > uA(ND; A) = uA(ND; W ) = 2 > uA(D; W ) = 1 uB(ND; A) = uB(ND; W ) = 3 > uB(D; A) = 2 > uB(D; W ) = 1 How can we represent this scenario as a game (in strategic form)? 6 / 26 International Crisis Game: NE Country B WA D 1; 1 3X; 2X Country A ND 2X; 3X 2; 3X I Is there something funny here? I Is there something funny here? I Specifically, (ND; W )? I Is there something funny here? -

Best Experienced Payoff Dynamics and Cooperation in the Centipede Game
Theoretical Economics 14 (2019), 1347–1385 1555-7561/20191347 Best experienced payoff dynamics and cooperation in the centipede game William H. Sandholm Department of Economics, University of Wisconsin Segismundo S. Izquierdo BioEcoUva, Department of Industrial Organization, Universidad de Valladolid Luis R. Izquierdo Department of Civil Engineering, Universidad de Burgos We study population game dynamics under which each revising agent tests each of his strategies a fixed number of times, with each play of each strategy being against a newly drawn opponent, and chooses the strategy whose total payoff was highest. In the centipede game, these best experienced payoff dynamics lead to co- operative play. When strategies are tested once, play at the almost globally stable state is concentrated on the last few nodes of the game, with the proportions of agents playing each strategy being largely independent of the length of the game. Testing strategies many times leads to cyclical play. Keywords. Evolutionary game theory, backward induction, centipede game, computational algebra. JEL classification. C72, C73. 1. Introduction The discrepancy between the conclusions of backward induction reasoning and ob- served behavior in certain canonical extensive form games is a basic puzzle of game the- ory. The centipede game (Rosenthal (1981)), the finitely repeated prisoner’s dilemma, and related examples can be viewed as models of relationships in which each partic- ipant has repeated opportunities to take costly actions that benefit his partner and in which there is a commonly known date at which the interaction will end. Experimen- tal and anecdotal evidence suggests that cooperative behavior may persist until close to William H. -
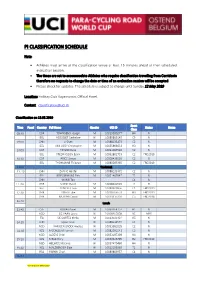
Pi Classification Schedule
PI CLASSIFICATION SCHEDULE Note: • Athletes must arrive at the classification venue at least 15 minutes ahead of their scheduled evaluation session. • The times are set to accommodate Athletes who require classification travelling from Corridonia therefore no requests to change the date or time of an evaluation session will be accepted. • Please check for updates. The schedule is subject to change until Sunday 12 May 2019 Location: Holiday Club Vayamundo, Official Hotel. Contact: [email protected] Classification on 13.05.2019 Sport Time Panel Country Full Name Gender UCI ID Status Notes Class 08:30 GBR TOWNSEND Joseph M 10019380277 H4 N BEL HOSSELET Catheline W 10089809149 C5 N 09:00 CHN LI Shan M 10088133473 C2 N BEL VAN LOOY Christophe M 10055886633 H3 N 10:00 GBR TAYLOR Ryan M 10093387540 C2 N BEL FREDRIKSSON Bjorn M 10062802733 C2 FRD2019 10:30 GBR PRICE Simon M 10008436556 C2 R BEL THOMANNE Thibaud M 10080285365 C2 FRD2019 11:00 Tea break 11 :10 CHN ZHANG Haofei M 10088133372 C2 N BEL KRIECKEMANS Dirk M 10091467647 T2 N CHN WANG Tao C4 N 11 :40 GBR STONE David M 10008440903 T2 R BEL CLINCKE Louis M 10080303856 C4 FRD2019 12:10 GBR JONES Luke M 10018766551 H3 FRD2019 GBR MURPHY David M 10019315310 C5 FRD2018 12:40 Lunch 13:40 CZE KOVAR Pavel M 10063464757 H1 N NED DE VAAN Laura W 10008465858 NE MRR ITA DE CORTES Mirko M 10013021424 H5 N 14:10 CHN QIAO Yuxin W 10088133574 C4 N NED VAN DEN BROEK Andrea W 10093581035 C2 N 14:40 NZL MCCALLUM Hamish M 10082591541 C3 N NED ALBERS Chiel M 10053197309 H4 N 15:10 NZL MEAD Rory M 10059646795 -

Lecture Notes
GRADUATE GAME THEORY LECTURE NOTES BY OMER TAMUZ California Institute of Technology 2018 Acknowledgments These lecture notes are partially adapted from Osborne and Rubinstein [29], Maschler, Solan and Zamir [23], lecture notes by Federico Echenique, and slides by Daron Acemoglu and Asu Ozdaglar. I am indebted to Seo Young (Silvia) Kim and Zhuofang Li for their help in finding and correcting many errors. Any comments or suggestions are welcome. 2 Contents 1 Extensive form games with perfect information 7 1.1 Tic-Tac-Toe ........................................ 7 1.2 The Sweet Fifteen Game ................................ 7 1.3 Chess ............................................ 7 1.4 Definition of extensive form games with perfect information ........... 10 1.5 The ultimatum game .................................. 10 1.6 Equilibria ......................................... 11 1.7 The centipede game ................................... 11 1.8 Subgames and subgame perfect equilibria ...................... 13 1.9 The dollar auction .................................... 14 1.10 Backward induction, Kuhn’s Theorem and a proof of Zermelo’s Theorem ... 15 2 Strategic form games 17 2.1 Definition ......................................... 17 2.2 Nash equilibria ...................................... 17 2.3 Classical examples .................................... 17 2.4 Dominated strategies .................................. 22 2.5 Repeated elimination of dominated strategies ................... 22 2.6 Dominant strategies .................................. -

Modeling Strategic Behavior1
Modeling Strategic Behavior1 A Graduate Introduction to Game Theory and Mechanism Design George J. Mailath Department of Economics, University of Pennsylvania Research School of Economics, Australian National University 1September 16, 2020, copyright by George J. Mailath. World Scientific Press published the November 02, 2018 version. Any significant correc- tions or changes are listed at the back. To Loretta Preface These notes are based on my lecture notes for Economics 703, a first-year graduate course that I have been teaching at the Eco- nomics Department, University of Pennsylvania, for many years. It is impossible to understand modern economics without knowl- edge of the basic tools of game theory and mechanism design. My goal in the course (and this book) is to teach those basic tools so that students can understand and appreciate the corpus of modern economic thought, and so contribute to it. A key theme in the course is the interplay between the formal development of the tools and their use in applications. At the same time, extensions of the results that are beyond the course, but im- portant for context are (briefly) discussed. While I provide more background verbally on many of the exam- ples, I assume that students have seen some undergraduate game theory (such as covered in Osborne, 2004, Tadelis, 2013, and Wat- son, 2013). In addition, some exposure to intermediate microeco- nomics and decision making under uncertainty is helpful. Since these are lecture notes for an introductory course, I have not tried to attribute every result or model described. The result is a somewhat random pattern of citations and references. -

Dynamic Games Under Bounded Rationality
Munich Personal RePEc Archive Dynamic Games under Bounded Rationality Zhao, Guo Southwest University for Nationalities 8 March 2015 Online at https://mpra.ub.uni-muenchen.de/62688/ MPRA Paper No. 62688, posted 09 Mar 2015 08:52 UTC Dynamic Games under Bounded Rationality By ZHAO GUO I propose a dynamic game model that is consistent with the paradigm of bounded rationality. Its main advantages over the traditional approach based on perfect rationality are that: (1) the strategy space is a chain-complete partially ordered set; (2) the response function is certain order-preserving map on strategy space; (3) the evolution of economic system can be described by the Dynamical System defined by the response function under iteration; (4) the existence of pure-strategy Nash equilibria can be guaranteed by fixed point theorems for ordered structures, rather than topological structures. This preference-response framework liberates economics from the utility concept, and constitutes a marriage of normal-form and extensive-form games. Among the common assumptions of classical existence theorems for competitive equilibrium, one is central. That is, individuals are assumed to have perfect rationality, so as to maximize their utilities (payoffs in game theoretic usage). With perfect rationality and perfect competition, the competitive equilibrium is completely determined, and the equilibrium depends only on their goals and their environments. With perfect rationality and perfect competition, the classical economic theory turns out to be deductive theory that requires almost no contact with empirical data once its assumptions are accepted as axioms (see Simon 1959). Zhao: Southwest University for Nationalities, Chengdu 610041, China (e-mail: [email protected]). -

Get Instruction Manual
We strive to ensure that our produc ts are of the highest quality and free of manufacturing defec ts or missing par ts. Howeve r, if you have any problems with your new product, please contact us toll free at: 1-88 8 - 577 - 4460 [email protected] Or w r it e t o: Victory Tailgate Customer Service Departmen t 2437 E Landstreet Rd Orlando,FL 32824 www.victorytailgate.com Please have your model number when inquiring about parts. When con t ac ting Escalade S por t s please provide your model numbe r , date code (i f applicable ), and pa rt nu mbe r i f reque sting a repla c emen t pa rt. The s e nu mbe rs a re loc ated on the p rodu ct, pa ckaging , and in thi s owne rs manual . Your Model Number : M01530W Date Code: 2-M01530W- -JL Purchase Date: PLEASE RETAIN THIS INSTRUCTION MANUAL FOR FUTURE REFERENCE All Rights Reserved © 2019 Escalade Spor ts 1 For Customer Service Call 1-888-577-4460 IMPORTANT! READ EACH STEP IN THIS MANUAL BEFORE YOU BEGIN THE ASSEMBLY. TWO (2) ADU LTS ARE REQUIRED TO ASSEMBLE THISDOUBLE SHOOTOUT Tools Needed: Allen Wrench (provided)Phillips Screwdriver Plyers ! Make sure you understand the following tips before you begin to assemble your basketball shootout. 1.This game (with Mechanical Scoring Arm) can be played outdoors in dry weather - but must be stored indoors. 2.Tighten hardware as instructed. 3.Do not over tighten hardware,as you could crush the tubing. 4.Some drawings or images in this manual may not look exactly like your product. -

Chemical Game Theory
Chemical Game Theory Jacob Kautzky Group Meeting February 26th, 2020 What is game theory? Game theory is the study of the ways in which interacting choices of rational agents produce outcomes with respect to the utilities of those agents Why do we care about game theory? 11 nobel prizes in economics 1994 – “for their pioneering analysis of equilibria in the thoery of non-cooperative games” John Nash Reinhard Selten John Harsanyi 2005 – “for having enhanced our understanding of conflict and cooperation through game-theory” Robert Aumann Thomas Schelling Why do we care about game theory? 2007 – “for having laid the foundatiouns of mechanism design theory” Leonid Hurwicz Eric Maskin Roger Myerson 2012 – “for the theory of stable allocations and the practice of market design” Alvin Roth Lloyd Shapley 2014 – “for his analysis of market power and regulation” Jean Tirole Why do we care about game theory? Mathematics Business Biology Engineering Sociology Philosophy Computer Science Political Science Chemistry Why do we care about game theory? Plato, 5th Century BCE Initial insights into game theory can be seen in Plato’s work Theories on prisoner desertions Cortez, 1517 Shakespeare’s Henry V, 1599 Hobbes’ Leviathan, 1651 Henry orders the French prisoners “burn the ships” executed infront of the French army First mathematical theory of games was published in 1944 by John von Neumann and Oskar Morgenstern Chemical Game Theory Basics of Game Theory Prisoners Dilemma Battle of the Sexes Rock Paper Scissors Centipede Game Iterated Prisoners Dilemma -

Contemporaneous Perfect Epsilon-Equilibria
Games and Economic Behavior 53 (2005) 126–140 www.elsevier.com/locate/geb Contemporaneous perfect epsilon-equilibria George J. Mailath a, Andrew Postlewaite a,∗, Larry Samuelson b a University of Pennsylvania b University of Wisconsin Received 8 January 2003 Available online 18 July 2005 Abstract We examine contemporaneous perfect ε-equilibria, in which a player’s actions after every history, evaluated at the point of deviation from the equilibrium, must be within ε of a best response. This concept implies, but is stronger than, Radner’s ex ante perfect ε-equilibrium. A strategy profile is a contemporaneous perfect ε-equilibrium of a game if it is a subgame perfect equilibrium in a perturbed game with nearly the same payoffs, with the converse holding for pure equilibria. 2005 Elsevier Inc. All rights reserved. JEL classification: C70; C72; C73 Keywords: Epsilon equilibrium; Ex ante payoff; Multistage game; Subgame perfect equilibrium 1. Introduction Analyzing a game begins with the construction of a model specifying the strategies of the players and the resulting payoffs. For many games, one cannot be positive that the specified payoffs are precisely correct. For the model to be useful, one must hope that its equilibria are close to those of the real game whenever the payoff misspecification is small. To ensure that an equilibrium of the model is close to a Nash equilibrium of every possible game with nearly the same payoffs, the appropriate solution concept in the model * Corresponding author. E-mail addresses: [email protected] (G.J. Mailath), [email protected] (A. Postlewaite), [email protected] (L. -

ELIGIBILITY Para-Cycling Athletes: Must Be a United States Citizen With
ELIGIBILITY Para-cycling Athletes: Must be a United States citizen with a USA racing nationality. LICENSING National Championships: Riders may have a current International or Domestic USA Cycling license (USA citizenship) or Foreign Federation license showing a USA racing nationality to register. World Championships Selection: Riders must have a current International USA Cycling license with a USA racing nationality on or before June 20, 2019 in order to be selected for the Team USA roster for the 2019 UCI Para-cycling Road World Championships. Selection procedures for the World Championships can be found on the U.S. Paralympics Cycling Website: https://www.teamusa.org/US- Paralympics/Sports/Cycling/Selection-Procedures REGULATIONS General: All events conducted under UCI Regulations, including UCI equipment regulations. Road Race and Time Trials: • No National Team Kit or National championship uniforms are allowed. • For the Road Race, only neutral service and official’s cars are allowed in the caravan. • For the Time Trial, bicycles and handcycles must be checked 15 minutes before the athlete’s assigned start time. Courtesy checks will be available from 1 hour before the first start. No follow vehicles are allowed. • For all sport classes in the road race, athletes are required to wear a helmet in the correct sport class color, or use an appropriately color helmet cover, as follows: RED MC5, WC5, MT2, MH4, WH4, MB WHITE MC4, WC4, MH3, WH3, WB, WT2 BLUE MC3, WC3, MH2, WT1 BLACK MH5, WH5, MC2, WC2, MT1 YELLOW MC1, WC1, WH2 GREEN MH1 ORANGE WH1 Handcycle Team Relay (TR): New National Championship event run under UCI and special regulations below: • Team Requirements: Teams eligible for the National Championship Team Relay, must be respect the following composition: o Teams of three athletes o Using the table below, the total of points for the three TR athletes may not be more than six (6) points which must include an athlete with a scoring point value of 1. -

Engineered Class Poles Including Steel SW, SWR, Concrete and Hybrid
Engineered Class Poles Including Steel SW, SWR, Concrete and Hybrid Expanded Standard Poles: Concrete Structure designs to 140’ heights and 20,000 lbs. tip load. Steel Hybrid As the need for wood alternative poles increases, now more than ever is the time to switch to Valmont Newmark steel, concrete and hybrid poles. Why Valmont Newmark? Recognized as an industry leader for quality and reliability, Valmont has been supplying utility structures since the 1970’s. Dependable structures are a priority and we utilize a proprietary design software, developed in-house and based on extensive testing, for all of our structural designs. We take great care in each step of the design and manufacturing process to ensure that our customers receive the highest quality product and on time delivery. By sharing manufacturing and engineering practices across our global network, we are better able to leverage our existing products, facilities and processes. As a result, we are the only company in the industry that provides a comprehensive product selection from a single source. Table of Contents Introduction ........................................................................... 2 - 3 Product Attributes ...................................................................... 4 Features and Benefits ................................................................. 5 Rapid Response Series ............................................................... 6 Ground Line Moment Quick Tables ....................................... 7 - 8 Standard Pole Classifications -

CS711: Introduction to Game Theory and Mechanism Design
CS711: Introduction to Game Theory and Mechanism Design Teacher: Swaprava Nath Extensive Form Games Extensive Form Games Chocolate Division Game: Suppose a mother gives his elder son two (indivisible) chocolates to share between him and his younger sister. She also warns that if there is any dispute in the sharing, she will take the chocolates back and nobody will get anything. The brother can propose the following sharing options: (2-0): brother gets two, sister gets nothing, or (1-1): both gets one each, or (0-2): both chocolates to the sister. After the brother proposes the sharing, his sister may \Accept" the division or \Reject" it. Brother 2-0 1-1 0-2 Sister ARARAR (2; 0) (0; 0) (1; 1)(0; 0) (0; 2) (0; 0) 1 / 16 Game Theory and Mechanism Design Extensive Form Games S1 = f2 − 0; 1 − 1; 0 − 2g S2 = fA; Rg × fA; Rg × fA; Rg = fAAA; AAR; ARA; ARR; RAA; RAR; RRA; RRRg u1(2 − 0;A) = 2; u1(1 − 1;A) = 1; u2(1 − 1;A) = 1; u2(0 − 2;A) = 2 u1(0 − 2;A) = u1(0 − 2;R) = u1(1 − 1;R) = u1(2 − 0;R) = 0 u2(0 − 2;R) = u2(1 − 1;R) = u2(2 − 0;R) = u2(2 − 0;A) = 0 P (?) = 1;P (2 − 0) = P (1 − 1) = P (0 − 2) = 2 X (2 − 0) = X (1 − 1) = X (0 − 2) = fA; Rg X (?) = f(2 − 0); (1 − 1); (0 − 2)g Z = f(2 − 0;A); (2 − 0;R); (1 − 1;A); (1 − 1;R); (0 − 2;A); (0 − 2;R)g H = f?; (2 − 0); (1 − 1); (0 − 2); (2 − 0;A); (2 − 0;R); (1 − 1;A); (1 − 1;R); (0 − 2;A); (0 − 2;R)g N = f1 (brother); 2 (sister)g;A = f2 − 0; 1 − 1; 0 − 2; A; Rg Representing the Chocolate Division Game Brother 2-0 1-1 0-2 Sister ARARAR (2; 0) (0; 0) (1; 1)(0; 0) (0; 2) (0; 0) 2 / 16 Game Theory