DOCSLIB.ORG

Appendix: Decimal, Hexadecimal and Binary Number Systems

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Appendix: Decimal, Hexadecimal and Binary Number Systems Appendix: Decimal, Hexadecimal and Binary Number Systems The decimal number system uses the ten digits 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 and is said to be a base 10 system. In any decimal number a digit is given a certain value that depends on its position in the given field of digits. The number 325, for example, is understood as 5 units plus 2 tens plus 3 hundreds and it can be interpreted as 5 x 10°, plus 2 x 101 , plus 3 x 102 or simply additions of multiple powers of 10. Any decimal number, including fractional decimal numbers, can be expressed this way. The hexadecimal number system uses sixteen digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E and F and is a base 16 system. As with the decimal number system, a digit has a value that is dependent on its position in a given field of digits. The first position in a hexadecimal number equates to the digit in that position multiplied by 16°. The second position equates to the digit times 161 and so on. The hexadecimal number 243 (written $243) may be interpreted as 3 x 16°,plus4 x 161 ,plus 2 x 162 which is 579. On this basis it is a simple matter to build up a table of figures for hexa­ decimal to decimal conversion, as shown in Table A. I. The second line of the table is 163 , 162 , 161 and tt;O, with all the other entries being multiples of that line. To use the table, the-entry for each hexadecimal digit and its corresponding position is simply added, since the multiplication has already been carried out. Example A.l. Hexadecimal to decimal conversion Given $3A4B $3000 is 12288 $ AOO is 2560 $ 40 is 64 $ B is 11 Hence $3A4B is 14923 249 250 MICROCOMPUTER APPLICATIONS IN STRUCTURAL ENGINEERING Table A.1 Hexadecimal-decimal conversion Hexadecimal Digit Position Digit 4th 3rd 2nd 1st 0 0 0 0 0 1 4096 256 16 1 2 8192 512 32 2 3 12288 768 48 3 4 16384 1024 64 4 5 20480 1280 80 5 6 24576 1536 96 6 7 28672 1792 112 7 8 32768 2048 128 8 9 36864 2304 144 9 A 40960 2560 160 10 B 45056 2816 176 11 c 49152 3072 192 12 D 53248 3328 208 13 E 57344 3584 224 14 F 61440 3840 240 15 For decimal to hexadecimal conversion, select the nearest number in the table to that given. This provides a hexadecimal digit and its position; repeat with the remainder. Example A.2. Decimal to hexadecimal conversion Given 5625 4096 is $1000 remainder 1529 1280 is $ 500 remainder 249 240 is $ FO remainder 9 9 is $ 9 remainder 0 Hence 5625 is $15F9 The binary number system uses only the two digits 0 and 1 and is a base 2 system. Again the digit has a value that is dependent on its position, this time equating to the digit multiplied by powers of 2, so that Table A.2 can be built up. The corresponding decimal-hexadecimal-binary relationship of Table A.3 follows immediately. APPENDIX: DECIMAL, HEXADECIMAL AND BINARY NUMBER SYSTEMS 251 Table A.2 Significance of binary digit position Decimal Value Binary Digit Position Power of2 Decimal 1st 20 1 2nd 21 2 3rd 22 4 4th 23 8 5th 24 16 6th 25 32 7th 26 64 8th 2' 128 Table A.3 Decimal-hexadecimal-binary Decimal Hexadecimal Binary 0 0 0000 1 1 0001 2 2 0010 3 3 0011 4 4 0100 5 5 0101 6 6 0110 7 7 0111 8 8 1000 9 9 1001 10 A 1010 11 B 1011 12 c 1100 13 D 1101 14 E 1110 15 F 1111 Conversion of decimal to binary and binary to decimal is conveniently carried out using hexadecimal code as an intermediate step. It should be noted that each digit in the fust position of a hexadecimal number can be represented by a 4-bit binary number. Each digit in the second position of a hexadecimal number can also be represented by a 4-bit binary number followed by 4 zero bits, while for a third position hexadecimal digit a 4-bit binary number followed by 8 zero bits is required. 252 MICROCOMPUTER APPLICATIONS IN STRUCTURAL ENGINEERING Example A.3. Hexadecimal to binary conversion Given $F3A9 $0009 is 1001 $00AO is 1010 0000 $0300 is 0011 0000 0000 $FOOO is 1111 0000 0000 0000 Hence $F3A9 is 1111 0011 1010 1001 In each case the bit pattern has come from Table A.3 using the hexadecimal digit without regard to its position. Conversion from binary to hexadecimal simply means taking the binary number in 4-bit patterns and assigning the cor­ responding hexadecimal digit to that position. Example A.4. Binary to hexadecimal conversion Given 1010 1100 0101 1001 1001 is $0009 0101 0000 is $0050 1100 0000 0000 is $0COO 1010 0000 0000 0000 is $AOOO Hence 1010 1100 0101 1001 is $AC59 Other number systems can be introduced on a similar basis and the octal number system using eight digits 0, 1, 2, 3, 4, 5, 6 and 7 is a base 8 system that is often used in digital computing. It should also be noted that fractional decimal numbers can be represented in other number systems. In the decimal system digits to the right of a decimal point are multiples of 10 raised to a negative power. The number 0.325 is (3 X 10-1) + (2 X 10-2) + (5 X 10-3) In a similar way in the binary system, positions to the right of a "decimal" point can be interpreted. The binary number 0.1000 is 1 x T 1 in decimal, which is 0.5. Some other fractional decimal to binary number conversions are given in Table A.4. Fractional decimal numbers are frequently expressed in exponent form and are referred to as floating point numbers. Indeed any non-integer number is usually described as a floating point number in the context of computers. The exponent indicates the number of positions that a decimal point has to be moved to give the number and this is given in the scientific notation represen­ tation of a decimal number. Any decimal number, apart from zero, can be written in the form ±Ax 10", where A is in the range 0.1 <;A< 1.0 APPENDIX: DECIMAL, HEXADECIMAL AND BINARY NUMBER SYSTEMS 253 Table A.4 Some fractional decimal to binary conversion Decimal Binary 0.5 (2-1) 0.1000 0.25 (T2) 0.0100 0.125 (T3) 0.0010 0.0625 (T4) 0.0001 Table A.S shows some decimal numbers in this form and in scientific notation. Table A.S Floating point number representation Number ±A X 10n Scientific Notation 5625.836 0.5625836 X 104 0.5625836E + 4 0.006258 o.6258ooo x 1 o-2 0.6258000E- 2 -15.23784 -0.1523784 X 102 -0.1523784E + 2 Such a method of representation need not be restricted to the decimal system. Any binary number, apart from zero, can be written in the form ±Ax 28 , where A is in the range of binary numbers O.I..;;A < 1 (which is the range of 1/2 o;;;;A < 1 in the decimal system). A is known as the mantissa and it should be noted that it is necessary to store only the sign, the mantissa and the exponent B to give a computer all the details of a floating point number. With an 8-bit microcomputer which uses a single byte to store the exponent, the range of B is from -127 to + 127 with B stored as B + 128; this ensures that B is always positive. The limit to the exponent arises since 127 + 128 is 255, which is the largest number that can be stored in 8 bits. The value B equal to 128 is reserved for the number zero. Table A.6 shows a series of binary numbers expressed in such a form. Only the bits of the mantissa to the right of the decimal point need be stored, the position of the decimal point being implied. Further, the most significant bit is always 1, so that this bit position can be used to indicate the sign of the number. For example, for a positive number this bit position is usually set to zero. 254 MICROCOMPUTER APPLICATIONS IN STRUCTURAL ENGINEERING Table A.6 Binary numbers in exponent form Number ±A x28 A B+ 12S 0001 0.1 X 21 0.1 129 0101 0.101 X 23 0.101 131 1000.1 0.10001 X 24 0.10001 132 1110 0.1110 X 24 0.1110 132 The previous discussion suggests a way in which a floating point number can be held in memory in a microcomputer. This can be done using 5 bytes, with the first byte holding the exponent in excess 12S mode and the remaining 4 bytes holding the mantissa. It is usually possible, by means of a suitable monitor on the microcomputer, to display the contents of memory locations byte by byte with the information returned in hexadecimal code. Alternatively a BASIC statement using the PEEK function can print out the byte contents in decimal code. For example, a monitor display of 5 bytes starting at a given memory address known to be the location of a floating point number could show S3 23 F3 5B AS which would be in hexadecimal code.
Load more

Recommended publications
  • Nondecimal Positional Systems
    M03_LONG0847_05_AIE_C03.qxd 9/17/07 10:38 AM Page 162 Not for Sale 162 CHAPTER 3 Numeration and Computation 3.2 Nondecimal Positional Systems In the preceding section, we discussed several numeration systems, including the decimal system in common use today. As already mentioned, the decimal system is a positional system based on 10. This is probably so because we have ten fingers and historically, as now, people often counted on their fingers. In the Did You Know box at the end of this section, we will give applications of positional systems that are based on whole numbers other than 10. One very useful application of bases other than ten is as a way to deepen our understanding of number systems, arithmetic in general, and our own decimal system. Although bases other than ten were in the K–5 curriculum in the past, they are not present currently. However, nondecimal positional systems are studied in the “math methods” course that is a part of an elementary education degree and may return to elementary school in the future. We will discuss addition and subtraction in base five in the next section and multiplication in base six in the following one. Base Five Notation For our purposes, perhaps the quickest route to understanding base five notation is to reconsider the abacus of Figure 3.1. This time, however, we allow only 5 beads to be moved forward on each wire. As before, we start with the wire to the students’ right (our left) and move 1 bead forward each time as we count 1, 2, 3, and so on.
    [Show full text]
  • TI 83/84: Scientific Notation on Your Calculator
    TI 83/84: Scientific Notation on your calculator this is above the comma, next to the square root! choose the proper MODE : Normal or Sci entering numbers: 2.39 x 106 on calculator: 2.39 2nd EE 6 ENTER reading numbers: 2.39E6 on the calculator means for us. • When you're in Normal mode, the calculator will write regular numbers unless they get too big or too small, when it will switch to scientific notation. • In Sci mode, the calculator displays every answer as scientific notation. • In both modes, you can type in numbers in scientific notation or as regular numbers. Humans should never, ever, ever write scientific notation using the calculator’s E notation! Try these problems. Answer in scientific notation, and round decimals to two places. 2.39 x 1016 (5) 2.39 x 109+ 4.7 x 10 10 (4) 4.7 x 10−3 3.01 103 1.07 10 0 2.39 10 5 4.94 10 10 5.09 1018 − 3.76 10−− 1 2.39 10 5 7.93 10 8 Remember to change your MODE back to Normal when you're done. Using the STORE key: Let's say that you want to store a number so that you can use it later, or that you want to store answers for several different variables, and then use them together in one problem. Here's how: Enter the number, then press STO (above the ON key), then press ALPHA and the letter you want. (The letters are in alphabetical order above the other keys.) Then press ENTER.
    [Show full text]
  • 13054-Duodecimal.Pdf
    Universal Multiple-Octet Coded Character Set International Organization for Standardization Organisation Internationale de Normalisation Международная организация по стандартизации Doc Type: Working Group Document Title: Proposal to encode Duodecimal Digit Forms in the UCS Author: Karl Pentzlin Status: Individual Contribution Action: For consideration by JTC1/SC2/WG2 and UTC Date: 2013-03-30 1. Introduction The duodecimal system (also called dozenal) is a positional numbering system using 12 as its base, similar to the well-known decimal (base 10) and hexadecimal (base 16) systems. Thus, it needs 12 digits, instead of ten digits like the decimal system. It is used by teachers to explain the decimal system by comparing it to an alternative, by hobbyists (see e.g. fig. 1), and by propagators who claim it being superior to the decimal system (mostly because thirds can be expressed by a finite number of digits in a "duodecimal point" presentation). • Besides mathematical and hobbyist publications, the duodecimal system has appeared as subject in the press (see e.g. [Bellos 2012] in the English newspaper "The Guardian" from 2012-12-12, where the lack of types to represent these digits correctly is explicitly stated). Such examples emphasize the need of the encoding of the digit forms proposed here. While it is common practice to represent the extra six digits needed for the hexadecimal system by the uppercase Latin capital letters A,B.C,D,E,F, there is no such established convention regarding the duodecimal system. Some proponents use the Latin letters T and E as the first letters of the English names of "ten" and "eleven" (which obviously is directly perceivable only for English speakers).
    [Show full text]
  • Zero Displacement Ternary Number System: the Most Economical Way of Representing Numbers
    Revista de Ciências da Computação, Volume III, Ano III, 2008, nº3 Zero Displacement Ternary Number System: the most economical way of representing numbers Fernando Guilherme Silvano Lobo Pimentel , Bank of Portugal, Email: [email protected] Abstract This paper concerns the efficiency of number systems. Following the identification of the most economical conventional integer number system, from a solid criteria, an improvement to such system’s representation economy is proposed which combines the representation efficiency of positional number systems without 0 with the possibility of representing the number 0. A modification to base 3 without 0 makes it possible to obtain a new number system which, according to the identified optimization criteria, becomes the most economic among all integer ones. Key Words: Positional Number Systems, Efficiency, Zero Resumo Este artigo aborda a questão da eficiência de sistemas de números. Partindo da identificação da mais económica base inteira de números de acordo com um critério preestabelecido, propõe-se um melhoramento à economia de representação nessa mesma base através da combinação da eficiência de representação de sistemas de números posicionais sem o zero com a possibilidade de representar o número zero. Uma modificação à base 3 sem zero permite a obtenção de um novo sistema de números que, de acordo com o critério de optimização identificado, é o sistema de representação mais económico entre os sistemas de números inteiros. Palavras-Chave: Sistemas de Números Posicionais, Eficiência, Zero 1 Introduction Counting systems are an indispensable tool in Computing Science. For reasons that are both technological and user friendliness, the performance of information processing depends heavily on the adopted numbering system.
    [Show full text]
  • Maths Week 2021
    Maths Week 2021 Survivor Series/Kia Mōrehurehu Monday Level 5 Questions What to do for students 1 You can work with one or two others. Teams can be different each day. 2 Do the tasks and write any working you did, along with your answers, in the spaces provided (or where your teacher says). 3 Your teacher will tell you how you can get the answers to the questions and/or have your work checked. 4 When you have finished each day, your teacher will give you a word or words from a proverb. 5 At the end of the week, put the words together in the right order and you will be able to find the complete proverb! Your teacher may ask you to explain what the proverb means. 6 Good luck. Task 1 – numbers in te reo Māori The following chart gives numbers in te reo Māori. Look at the chart carefully and note the patterns in the way the names are built up from 10 onwards. Work out what each of the numbers in the following calculations is, do each calculation, and write the answer in te reo Māori. Question Answer (a) whitu + toru (b) whā x wa (c) tekau mā waru – rua (d) ono tekau ma whā + rua tekau ma iwa (e) toru tekau ma rua + waru x tekau mā ono Task 2 - Roman numerals The picture shows the Roman Emperor, Julius Caesar, who was born in the year 100 BC. (a) How many years ago was 100 BC? You may have seen places where numbers have been written in Roman numerals.
    [Show full text]
  • Primitive Number Types
    Primitive number types Values of each of the primitive number types Java has these 4 primitive integral types: byte: A value occupies 1 byte (8 bits). The range of values is -2^7..2^7-1, or -128..127 short: A value occupies 2 bytes (16 bits). The range of values is -2^15..2^15-1 int: A value occupies 4 bytes (32 bits). The range of values is -2^31..2^31-1 long: A value occupies 8 bytes (64 bits). The range of values is -2^63..2^63-1 and two “floating-point” types, whose values are approximations to the real numbers: float: A value occupies 4 bytes (32 bits). double: A value occupies 8 bytes (64 bits). Values of the integral types are maintained in two’s complement notation (see the dictionary entry for two’s complement notation). A discussion of floating-point values is outside the scope of this website, except to say that some bits are used for the mantissa and some for the exponent and that infinity and NaN (not a number) are both floating-point values. We don’t discuss this further. Generally, one uses mainly types int and double. But if you are declaring a large array and you know that the values fit in a byte, you can save ¾ of the space using a byte array instead of an int array, e.g. byte[] b= new byte[1000]; Operations on the primitive integer types Types byte and short have no operations. Instead, operations on their values int and long operations are treated as if the values were of type int.
    [Show full text]
  • The Hexadecimal Number System and Memory Addressing
    C5537_App C_1107_03/16/2005 APPENDIX C The Hexadecimal Number System and Memory Addressing nderstanding the number system and the coding system that computers use to U store data and communicate with each other is fundamental to understanding how computers work. Early attempts to invent an electronic computing device met with disappointing results as long as inventors tried to use the decimal number sys- tem, with the digits 0–9. Then John Atanasoff proposed using a coding system that expressed everything in terms of different sequences of only two numerals: one repre- sented by the presence of a charge and one represented by the absence of a charge. The numbering system that can be supported by the expression of only two numerals is called base 2, or binary; it was invented by Ada Lovelace many years before, using the numerals 0 and 1. Under Atanasoff’s design, all numbers and other characters would be converted to this binary number system, and all storage, comparisons, and arithmetic would be done using it. Even today, this is one of the basic principles of computers. Every character or number entered into a computer is first converted into a series of 0s and 1s. Many coding schemes and techniques have been invented to manipulate these 0s and 1s, called bits for binary digits. The most widespread binary coding scheme for microcomputers, which is recog- nized as the microcomputer standard, is called ASCII (American Standard Code for Information Interchange). (Appendix B lists the binary code for the basic 127- character set.) In ASCII, each character is assigned an 8-bit code called a byte.
    [Show full text]
  • C++ Data Types
    Software Design & Programming I Starting Out with C++ (From Control Structures through Objects) 7th Edition Written by: Tony Gaddis Pearson - Addison Wesley ISBN: 13-978-0-132-57625-3 Chapter 2 (Part II) Introduction to C++ The char Data Type (Sample Program) Character and String Constants The char Data Type Program 2-12 assigns character constants to the variable letter. Anytime a program works with a character, it internally works with the code used to represent that character, so this program is still assigning the values 65 and 66 to letter. Character constants can only hold a single character. To store a series of characters in a constant we need a string constant. In the following example, 'H' is a character constant and "Hello" is a string constant. Notice that a character constant is enclosed in single quotation marks whereas a string constant is enclosed in double quotation marks. cout << ‘H’ << endl; cout << “Hello” << endl; The char Data Type Strings, which allow a series of characters to be stored in consecutive memory locations, can be virtually any length. This means that there must be some way for the program to know how long the string is. In C++ this is done by appending an extra byte to the end of string constants. In this last byte, the number 0 is stored. It is called the null terminator or null character and marks the end of the string. Don’t confuse the null terminator with the character '0'. If you look at Appendix A you will see that the character '0' has ASCII code 48, whereas the null terminator has ASCII code 0.
    [Show full text]
  • Floating Point Numbers
    Floating Point Numbers CS031 September 12, 2011 Motivation We’ve seen how unsigned and signed integers are represented by a computer. We’d like to represent decimal numbers like 3.7510 as well. By learning how these numbers are represented in hardware, we can understand and avoid pitfalls of using them in our code. Fixed-Point Binary Representation Fractional numbers are represented in binary much like integers are, but negative exponents and a decimal point are used. 3.7510 = 2+1+0.5+0.25 1 0 -1 -2 = 2 +2 +2 +2 = 11.112 Not all numbers have a finite representation: 0.110 = 0.0625+0.03125+0.0078125+… -4 -5 -8 -9 = 2 +2 +2 +2 +… = 0.00011001100110011… 2 Computer Representation Goals Fixed-point representation assumes no space limitations, so it’s infeasible here. Assume we have 32 bits per number. We want to represent as many decimal numbers as we can, don’t want to sacrifice range. Adding two numbers should be as similar to adding signed integers as possible. Comparing two numbers should be straightforward and intuitive in this representation. The Challenges How many distinct numbers can we represent with 32 bits? Answer: 232 We must decide which numbers to represent. Suppose we want to represent both 3.7510 = 11.112 and 7.510 = 111.12. How will the computer distinguish between them in our representation? Excursus – Scientific Notation 913.8 = 91.38 x 101 = 9.138 x 102 = 0.9138 x 103 We call the final 3 representations scientific notation. It’s standard to use the format 9.138 x 102 (exactly one non-zero digit before the decimal point) for a unique representation.
    [Show full text]
  • Floating Point Numbers and Arithmetic
    Overview Floating Point Numbers & • Floating Point Numbers Arithmetic • Motivation: Decimal Scientific Notation – Binary Scientific Notation • Floating Point Representation inside computer (binary) – Greater range, precision • Decimal to Floating Point conversion, and vice versa • Big Idea: Type is not associated with data • MIPS floating point instructions, registers CS 160 Ward 1 CS 160 Ward 2 Review of Numbers Other Numbers •What about other numbers? • Computers are made to deal with –Very large numbers? (seconds/century) numbers 9 3,155,760,00010 (3.1557610 x 10 ) • What can we represent in N bits? –Very small numbers? (atomic diameter) -8 – Unsigned integers: 0.0000000110 (1.010 x 10 ) 0to2N -1 –Rationals (repeating pattern) 2/3 (0.666666666. .) – Signed Integers (Two’s Complement) (N-1) (N-1) –Irrationals -2 to 2 -1 21/2 (1.414213562373. .) –Transcendentals e (2.718...), π (3.141...) •All represented in scientific notation CS 160 Ward 3 CS 160 Ward 4 Scientific Notation Review Scientific Notation for Binary Numbers mantissa exponent Mantissa exponent 23 -1 6.02 x 10 1.0two x 2 decimal point radix (base) “binary point” radix (base) •Computer arithmetic that supports it called •Normalized form: no leadings 0s floating point, because it represents (exactly one digit to left of decimal point) numbers where binary point is not fixed, as it is for integers •Alternatives to representing 1/1,000,000,000 –Declare such variable in C as float –Normalized: 1.0 x 10-9 –Not normalized: 0.1 x 10-8, 10.0 x 10-10 CS 160 Ward 5 CS 160 Ward 6 Floating
    [Show full text]
  • 2 1 2 = 30 60 and 1
    Math 153 Spring 2010 R. Schultz SOLUTIONS TO EXERCISES FROM math153exercises01.pdf As usual, \Burton" refers to the Seventh Edition of the course text by Burton (the page numbers for the Sixth Edition may be off slightly). Problems from Burton, p. 28 3. The fraction 1=6 is equal to 10=60 and therefore the sexagesimal expression is 0;10. To find the expansion for 1=9 we need to solve 1=9 = x=60. By elementary algebra this means 2 9x = 60 or x = 6 3 . Thus 6 2 1 6 40 1 x = + = + 60 3 · 60 60 60 · 60 which yields the sexagsimal expression 0; 10; 40 for 1/9. Finding the expression for 1/5 just amounts to writing this as 12/60, so the form here is 0;12. 1 1 30 To find 1=24 we again write 1=24 = x=60 and solve for x to get x = 2 2 . Now 2 = 60 and therefore we can proceed as in the second example to conclude that the sexagesimal form for 1/24 is 0;2,30. 1 One proceeds similarly for 1/40, solving 1=40 = x=60 to get x = 1 2 . Much as in the preceding discussion this yields the form 0;1,30. Finally, the same method leads to the equation 5=12 = x=60, which implies that 5/12 has the sexagesimal form 0;25. 4. We shall only rewrite these in standard base 10 fractional notation. The answers are in the back of Burton. (a) The sexagesimal number 1,23,45 is equal to 1 3600 + 23 60 + 45.
    [Show full text]
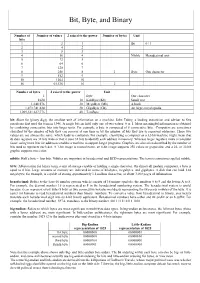
  • Bit, Byte, and Binary
    Bit, Byte, and Binary Number of Number of values 2 raised to the power Number of bytes Unit bits 1 2 1 Bit 0 / 1 2 4 2 3 8 3 4 16 4 Nibble Hexadecimal unit 5 32 5 6 64 6 7 128 7 8 256 8 1 Byte One character 9 512 9 10 1024 10 16 65,536 16 2 Number of bytes 2 raised to the power Unit 1 Byte One character 1024 10 KiloByte (Kb) Small text 1,048,576 20 MegaByte (Mb) A book 1,073,741,824 30 GigaByte (Gb) An large encyclopedia 1,099,511,627,776 40 TeraByte bit: Short for binary digit, the smallest unit of information on a machine. John Tukey, a leading statistician and adviser to five presidents first used the term in 1946. A single bit can hold only one of two values: 0 or 1. More meaningful information is obtained by combining consecutive bits into larger units. For example, a byte is composed of 8 consecutive bits. Computers are sometimes classified by the number of bits they can process at one time or by the number of bits they use to represent addresses. These two values are not always the same, which leads to confusion. For example, classifying a computer as a 32-bit machine might mean that its data registers are 32 bits wide or that it uses 32 bits to identify each address in memory. Whereas larger registers make a computer faster, using more bits for addresses enables a machine to support larger programs.
    [Show full text]