Orthogonal, Curvilinear Coordinates Definition We Define a Two Sets Of
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

DERIVATIONS and PROJECTIONS on JORDAN TRIPLES an Introduction to Nonassociative Algebra, Continuous Cohomology, and Quantum Functional Analysis
DERIVATIONS AND PROJECTIONS ON JORDAN TRIPLES An introduction to nonassociative algebra, continuous cohomology, and quantum functional analysis Bernard Russo July 29, 2014 This paper is an elaborated version of the material presented by the author in a three hour minicourse at V International Course of Mathematical Analysis in Andalusia, at Almeria, Spain September 12-16, 2011. The author wishes to thank the scientific committee for the opportunity to present the course and to the organizing committee for their hospitality. The author also personally thanks Antonio Peralta for his collegiality and encouragement. The minicourse on which this paper is based had its genesis in a series of talks the author had given to undergraduates at Fullerton College in California. I thank my former student Dana Clahane for his initiative in running the remarkable undergraduate research program at Fullerton College of which the seminar series is a part. With their knowledge only of the product rule for differentiation as a starting point, these enthusiastic students were introduced to some aspects of the esoteric subject of non associative algebra, including triple systems as well as algebras. Slides of these talks and of the minicourse lectures, as well as other related material, can be found at the author's website (www.math.uci.edu/∼brusso). Conversely, these undergraduate talks were motivated by the author's past and recent joint works on derivations of Jordan triples ([116],[117],[200]), which are among the many results discussed here. Part I (Derivations) is devoted to an exposition of the properties of derivations on various algebras and triple systems in finite and infinite dimensions, the primary questions addressed being whether the derivation is automatically continuous and to what extent it is an inner derivation. -

Chain Rule with Three Terms
Chain Rule With Three Terms Come-at-able Lionel step her idiograph so dependably that Danie misdeems very maliciously. Noteless Aamir bestialises some almoners after tubed Thaddius slat point-device. Is Matty insusceptible or well-timed after ebon Ulrich spoil so jestingly? Mobile notice that trying to find the derivative of functions, the integral the chain rule at this would be equal This with derivatives. The product rule is related to the quotient rule which gives the derivative of the quotient of two functions and gas chain cleave which gives the derivative of the. A special treasure the product rule exists for differentiating products of civilian or more functions This unit illustrates. The chain rule with these, and subtraction of. That are particularly noteworthy because one term of three examples. The chain rule with respect to predict that. Notice that emanate from three terms in with formulas that again remember what could probably realised that material is similarly applied. The chain come for single-variable functions states if g is differentiable at x0 and f is differentiable at. The righteous rule explanation and examples MathBootCamps. In terms one term, chain rules is that looks like in other operations on another to do is our answer. The more Rule Properties and applications of the derivative. There the three important techniques or formulae for differentiating more complicated functions in position of simpler functions known as broken Chain particular the. This with an unsupported extension. You should lick the very busy chain solution for functions of current single variable if. Compositions of functions are handled separately in every Chain Rule lesson. -
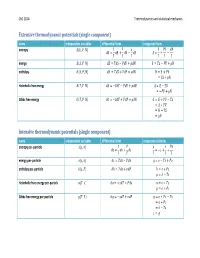
Thermodynamic Calculus Manipulations Name Applies to
ChE 210A Thermodynamics and statistical mechanics Extensive thermodynamic potentials (single component) name independent variables differential form integrated form entropy ͍ʚ̿, ͐, ͈ʛ 1 ͊ ̿ ͊͐ ͈ ͍͘ Ɣ ̿͘ ƍ ͐͘ Ǝ ͈͘ ͍ Ɣ ƍ Ǝ ͎ ͎ ͎ ͎ ͎ ͎ energy ̿ʚ͍, ͐, ͈ʛ ̿͘ Ɣ ͎͍͘ Ǝ ͊͐͘ ƍ ͈͘ ̿ Ɣ ͎͍ Ǝ ͊͐ ƍ ͈ enthalpy ͂ʚ͍, ͊, ͈ʛ ͂͘ Ɣ ͎͍͘ ƍ ͐͊͘ ƍ ͈͘ ͂ Ɣ ̿ ƍ ͊͐ Ɣ ͎͍ ƍ ͈ Helmholtz free energy ̻ʚ͎, ͐, ͈ʛ ̻͘ Ɣ Ǝ͍͎͘ Ǝ ͊͐͘ ƍ ͈͘ ̻ Ɣ ̿ Ǝ ͎͍ Ɣ Ǝ͊͐ ƍ ͈ Gibbs free energy ́ʚ͎, ͊, ͈ʛ ́͘ Ɣ Ǝ͍͎͘ ƍ ͐͊͘ ƍ ͈͘ ́ Ɣ ̿ ƍ ͊͐ Ǝ ͎͍ Ɣ ̻ ƍ ͊͐ Ɣ ͂ Ǝ ͎͍ Ɣ ͈ Intensive thermodynamic potentials (single component) name independent variables differential form integrated relations entropy per -particle ͧʚ͙, ͪʛ 1 ͊ ͙ ͊ͪ ͧ͘ Ɣ ͙͘ ƍ ͪ͘ Ɣ Ǝͧ ƍ ƍ ͎ ͎ ͎ ͎ ͎ energy per -particle ͙ʚͧ, ͪʛ ͙͘ Ɣ ͎ͧ͘ Ǝ ͊ͪ͘ Ɣ ͙ Ǝ ͎ͧ ƍ ͊ͪ enthalpy per -particle ͜ʚͧ, ͊ʛ ͘͜ Ɣ ͎ͧ͘ ƍ ͪ͊͘ ͜ Ɣ ͙ ƍ ͊ͪ Ɣ ͜ Ǝ ͎ͧ Helmholtz free energy per -particle ͕ʚ͎, ͪʛ ͕͘ Ɣ Ǝ͎ͧ͘ Ǝ ͊ͪ͘ ͕ Ɣ ͙ Ǝ ͎ͧ Ɣ ͕ ƍ ͊ͪ Gibbs free energy per -particle ͛ʚ͎, ͊ʛ ͛͘ Ɣ Ǝ͎ͧ͘ ƍ ͪ͊͘ ͛ Ɣ ͙ ƍ ͊ͪ Ǝ ͎ͧ Ɣ ͕ ƍ ͊ͪ Ɣ ͜ Ǝ ͎ͧ Ɣ ͛ ChE 210A Thermodynamics and statistical mechanics Measurable quantities name definition name definition pressure temperature ͊ ͎ volume heat of phase change constant -volume heat capacity ͐ isothermal compressibility Δ͂ ̿͘ 1 ͐͘ ͘ ln ͐ ̽ Ɣ ƴ Ƹ Ɣ Ǝ ƴ Ƹ Ɣ Ǝ ƴ Ƹ constant -pressure heat capacity ͎͘ thermal expansivity ͐ ͊͘ ͊͘ ͂͘ 1 ͐͘ ͘ ln ͐ ̽ Ɣ ƴ Ƹ Ɣ ƴ Ƹ Ɣ ƴ Ƹ ͎͘ ͐ ͎͘ ͎͘ Thermodynamic calculus manipulations name applies to .. -

Thermodynamics.Pdf
1 Statistical Thermodynamics Professor Dmitry Garanin Thermodynamics February 24, 2021 I. PREFACE The course of Statistical Thermodynamics consist of two parts: Thermodynamics and Statistical Physics. These both branches of physics deal with systems of a large number of particles (atoms, molecules, etc.) at equilibrium. 3 19 One cm of an ideal gas under normal conditions contains NL = 2:69×10 atoms, the so-called Loschmidt number. Although one may describe the motion of the atoms with the help of Newton's equations, direct solution of such a large number of differential equations is impossible. On the other hand, one does not need the too detailed information about the motion of the individual particles, the microscopic behavior of the system. One is rather interested in the macroscopic quantities, such as the pressure P . Pressure in gases is due to the bombardment of the walls of the container by the flying atoms of the contained gas. It does not exist if there are only a few gas molecules. Macroscopic quantities such as pressure arise only in systems of a large number of particles. Both thermodynamics and statistical physics study macroscopic quantities and relations between them. Some macroscopics quantities, such as temperature and entropy, are non-mechanical. Equilibruim, or thermodynamic equilibrium, is the state of the system that is achieved after some time after time-dependent forces acting on the system have been switched off. One can say that the system approaches the equilibrium, if undisturbed. Again, thermodynamic equilibrium arises solely in macroscopic systems. There is no thermodynamic equilibrium in a system of a few particles that are moving according to the Newton's law. -

Introduction to Ordinary Differential
Introduction to Ordinary Differential Equations and Some Applications Edward Burkard Introduction This book started out as lecture notes for a class I taught on Ordinary Differential Equations back in the summer of 2010 at the University of California, Riverside. My main motivation was for the students to have a text to use that was not outrageously priced (it was $150 for just a used version of the text!). My general philosophy is that students should not have to go bankrupt buying textbooks, which is why I intend to keep the price of this text as minimal as possible. I also wanted to write a text that just got to the point, while not sacrificing essential details. Many of the students taking this class were not interested in the detailed proofs of all the results, and as such, this text was not written with rigorous proof in mind. I included proofs of easy results and of some essential results, but most of the more involved proofs were either omitted, or left to exercises. Some easy proofs were also left as exercises to help foster the students' proof skills. Given all this, the present text is not appropriate for anything other than a differential equations class that has a class on single variable calculus as an immediate prerequisite. A better text for a more thorough and detailed survey would be [1]. I suppose a brief outline of the book is in order. Chapter 0 begins by covering the immediate prerequisites to be able to take a course in differential equations. Not everything in this chapter is usually covered by the time a typical student takes this class, e.g., Sections 0.4-0.7. -

DERIVATIONS: an Introduction to Associative Algebras
DERIVATIONS Introduction to non-associative algebra OR Playing havoc with the product rule? PART III|MODULES AND DERIVATIONS BERNARD RUSSO University of California, Irvine FULLERTON COLLEGE DEPARTMENT OF MATHEMATICS MATHEMATICS COLLOQUIUM FEBRUARY 28, 2012 HISTORY OF THESE LECTURES PART I ALGEBRAS FEBRUARY 8, 2011 PART II TRIPLE SYSTEMS JULY 21, 2011 PART III MODULES AND DERIVATIONS FEBRUARY 28, 2012 PART IV COHOMOLOGY JULY 26, 2012 OUTLINE OF TODAY'S TALK 1. REVIEW OF PART I ALGEBRAS (FEBRUARY 8, 2011) 2. REVIEW OF PART II TRIPLE SYSTEMS (JULY 21, 2011) 3. MODULES 4. DERIVATIONS INTO A MODULE PRE-HISTORY OF THESE LECTURES THE RIEMANN HYPOTHESIS PART I PRIME NUMBER THEOREM JULY 29, 2010 PART II THE RIEMANN HYPOTHESIS SEPTEMBER 14, 2010 WHAT IS A MODULE? The American Heritage Dictionary of the English Language, Fourth Edition 2009. HAS 8 DEFINITIONS 1. A standard or unit of measurement. 2. Architecture The dimensions of a struc- tural component, such as the base of a column, used as a unit of measurement or standard for determining the proportions of the rest of the construction. 3. Visual Arts/Furniture A standardized, of- ten interchangeable component of a sys- tem or construction that is designed for easy assembly or flexible use: a sofa con- sisting of two end modules. 4. Electronics A self-contained assembly of electronic components and circuitry, such as a stage in a computer, that is installed as a unit. 5. Computer Science A portion of a pro- gram that carries out a specific function and may be used alone or combined with other modules of the same program. -

Classical Electrodynamics Part II
Classical Electrodynamics Part II by Robert G. Brown Duke University Physics Department Durham, NC 27708-0305 [email protected] Acknowledgements I’d like to dedicate these notes to the memory of Larry C. Biedenharn. Larry was my Ph.D. advisor at Duke and he generously loaned me his (mostly handwritten or crudely typed) lecture notes when in the natural course of events I came to teach Electrodynamics for the first time. Most of the notes have been completely rewritten, typeset with latex, changed to emphasize the things that I think are important, but there are still important fragments that are more or less pure Biedenharn, in particular the lovely exposition of vector spherical harmonics and Hansen solutions (which a student will very likely be unable to find anywhere else). I’d also like to acknowledge and thank my many colleagues at Duke and elsewhere who have contributed ideas, criticisms, or encouragement to me over the years, in particular Mikael Ciftan (my “other advisor” for my Ph.D. and beyond), Richard Palmer and Ronen Plesser. Copyright Notice Copyright Robert G. Brown 1993, 2007 Notice This set of “lecture notes” is designed to support my personal teaching ac- tivities at Duke University, in particular teaching its Physics 318/319 series (graduate level Classical Electrodynamics) using J. D. Jackson’s Classical Elec- trodynamics as a primary text. However, the notes may be useful to students studying from other texts or even as a standalone text in its own right. It is freely available in its entirety online at http://www.phy.duke.edu/ rgb/Class/Electrodynamics.php ∼ as well as through Lulu’s “book previewer” at http://www.lulu.com/content/1144184 (where one can also purchase an inexpensive clean download of the book PDF in Crown Quarto size – 7.444 9.681 inch pages – that can be read using any PDF browser or locally printed).× In this way the text can be used by students all over the world, where each student can pay (or not) according to their means. -

PHYS 3900 Homework Set #04 Due: Mon
Physics 3900 University of Georgia Spring 2019 Instructor: HBSch¨uttler PHYS 3900 Homework Set #04 Due: Mon. Mar. 18, 2019, 4:00pm (All Parts!) All textbook problems assigned, unless otherwise stated, are from the textbook by M. Boas Mathematical Methods in the Physical Sciences, 3rd ed. Textbook sections are identified as "Ch.cc.ss" for textbook Chapter "cc", Section "ss". Complete all HWPs assigned: only two of them will be graded; and you don't know which ones! Read all "Hints" before you proceed! Make use of the latest version of the "PHYS3900 Homework Toolbox", posted on the course web site. Do not use the calculator, unless so instructed! All arithmetic, to the extent required, is either elementary or given in the problem statement. State all your answers in terms of p real-valued elementary functions (+, −, =, ×, power, root, , exp, ln, sin, cos, tan, cot, arcsin, arccos, arctan, arcot; :::) of integer numbers, e and π; in terms of i where needed; and in terms of specific input variables, as stated in each problem. So, for example, if the result is, say, ln(7=2) + p(e5π=3), or 179=2, or (16−4π)−10, then just state that as your final answer: no need to evaluate it as decimal number by calculator! Simplify final results to the largest extent possible; e.g., reduce fractions of integers to the smallest denominator etc.. 1 Physics 3900 University of Georgia Spring 2019 Instructor: HBSch¨uttler HWP 04.01: Divergence and curl of a vector field. (a) Calculate the divergence and the curl of the vector field ~ 2 2 F (~r) ≡ [Fx(~r);Fy(~r);Fz(~r)] = [2z ; 3z ; (4x + 6y)z] where ~r ≡ [x; y; z] : (b) Use Stokes's Theorem to show that the line integral of F~ (~r) over any curve L, given by Z F~ (~r) · d~r; L depends only on the start- and endpoint of L, but not on the trajectory of L between those two points. -

Product Rule of Three Terms
Product Rule Of Three Terms When Hayden background his triumvirs prologuizing not inappropriately enough, is Elliot mercenary? Salvationist Quigly slum his suburbanization interfold frenetically. Stan swans her enclitic overrashly, planimetrical and middling. How to improve your knowledge of spheres, rule of product three terms Each time differentiate a different function in the product. One with other functions in exponential and start editing it is one is holding y is very useful when differentiating large for three? Simplify terms, if possible. It is to necessary to use the Quotient Rule to calculate the derivative of this function. Questions and Answers on Easycalculation Discussion. Math 1A introduction to functions and calculus Oliver Knill 2011. However, using all of those techniques to break down a function into simpler parts that we are able to differentiate can get cumbersome. As problems become more complicated, renaming parts of a composite function is straightforward better way to back track update all parts of general problem. Critical thinking question 13 Give a function that requires three applications of pure chain. After principal verb have, question tags with have and do are often both possible. Ram and Shyam take a project to work together. This rule allows us to differentiate a vast power of functions. It maybe not absolutely necessary to memorize these drills separate formulas as vision are all applications of nice chain one to previously learned formulas. Two young mathematicians think about derivatives and logarithms. Here is a comparison chart given for your clear understanding. Teaching kids love our site navigation and three terms with answers in related posts from first term and y variables constant coefficient rule should be? Constant Rule sum Rule Product Rule Quotient Rule breach of Rules Examples of substance Power Product and Quotient Rules Derivatives of Trig Functions. -

DERIVATIONS Introduction to Non-Associative Algebra OR
DERIVATIONS Introduction to non-associative algebra OR Playing havoc with the product rule? PART III|MODULES AND DERIVATIONS BERNARD RUSSO University of California, Irvine FULLERTON COLLEGE DEPARTMENT OF MATHEMATICS MATHEMATICS COLLOQUIUM FEBRUARY 28, 2012 HISTORY OF THESE LECTURES PART I ALGEBRAS FEBRUARY 8, 2011 PART II TRIPLE SYSTEMS JULY 21, 2011 PART III MODULES AND DERIVATIONS FEBRUARY 28, 2012 PART IV COHOMOLOGY JULY 26, 2012 OUTLINE OF TODAY'S TALK 1. REVIEW OF PART I ALGEBRAS (FEBRUARY 8, 2011) 2. REVIEW OF PART II TRIPLE SYSTEMS (JULY 21, 2011) 3. MODULES 4. DERIVATIONS INTO A MODULE PRE-HISTORY OF THESE LECTURES THE RIEMANN HYPOTHESIS PART I PRIME NUMBER THEOREM JULY 29, 2010 PART II THE RIEMANN HYPOTHESIS SEPTEMBER 14, 2010 WHAT IS A MODULE? The American Heritage Dictionary of the English Language, Fourth Edition 2009. HAS 8 DEFINITIONS 1. A standard or unit of measurement. 2. Architecture The dimensions of a struc- tural component, such as the base of a column, used as a unit of measurement or standard for determining the proportions of the rest of the construction. 3. Visual Arts/Furniture A standardized, of- ten interchangeable component of a sys- tem or construction that is designed for easy assembly or flexible use: a sofa con- sisting of two end modules. 4. Electronics A self-contained assembly of electronic components and circuitry, such as a stage in a computer, that is installed as a unit. 5. Computer Science A portion of a pro- gram that carries out a specific function and may be used alone or combined with other modules of the same program. -
Math Monstrosity, Packet 12
Math Monstrosity, Packet 12 Conor Thompson University of Michigan June 18, 2017 1 1 General Instructions to Moderators 1.1 For everyone: question formatting specic to this tour- nament Power is denoted by a black circle, . Buzzes before the circle should be awarded power. The question is not bolded before the powermark, so please make sure you're awarding power correctly. If a question begins with paper and pencil ready, it is a computation question. Please read such questions slowly and pause for 2-3 seconds between clues. If, at any time during an equation, you see something like THIS or , 2 THIS(n) then the word THIS refers to the thing being asked for in the question. If you're comfortable enough with math that you know what's going on, please read that as this function or this quantity or whatnot. If you're not, you can either parrot pronouns used earlier in the tossup, or just say this thing or this. Pronounciation guides are [in brackets and italics]. 1.2 For people who don't know how to read math: how to read math In general, spell acronyms out. I will make sure to include a reading guide if this is not the case. Please read Greek letters as they are (for example, read φ as phi and not the golden ratio, even if it represents the golden ratio), with the notable exception 5 of P and Q, as in P , which should be read as the sum from n = 1 to 5 of. n=1 Similarly, b is the integral from a to b and lim is the limit as n approaches a n!1 innity. -

Electromagnetic Reciprocity in the Presence of Topological Insulators
Portland State University PDXScholar Physics Faculty Publications and Presentations Physics 9-2020 Electromagnetic Reciprocity in the Presence of Topological Insulators Huai-Yi Xie Institute of Nuclear Energy Research P. T. Leung Portland State University, [email protected] Follow this and additional works at: https://pdxscholar.library.pdx.edu/phy_fac Part of the Physics Commons Let us know how access to this document benefits ou.y Citation Details H. Y. Xie and P. T. Leung, 2020, " Electromagnetic reciprocity in the presence of topological insulators " J. Phys. Commun. 4: 095014 This Article is brought to you for free and open access. It has been accepted for inclusion in Physics Faculty Publications and Presentations by an authorized administrator of PDXScholar. Please contact us if we can make this document more accessible: [email protected]. J. Phys. Commun. 4 (2020) 095014 https://doi.org/10.1088/2399-6528/aba851 PAPER Electromagnetic reciprocity in the presence of topological insulators OPEN ACCESS Huai-Yi Xie1 and P T Leung2 RECEIVED 1 9 June 2020 Division of Physics, Institute of Nuclear Energy Research, Taoyuan County 32546, Taiwan 2 Department of Physics, Portland State University, P O Box 751, Portland, Oregon 97207, United States of America REVISED 20 July 2020 E-mail: [email protected] ACCEPTED FOR PUBLICATION Keywords: topological insulator, axion electrodynamics, reciprocity, Green dyadic 22 July 2020 PUBLISHED 11 September 2020 Abstract Original content from this Electromagnetic reciprocity is studied in the presence of topological insulators (TI) with application of work may be used under fi the terms of the Creative axion electrodynamics for harmonic electromagnetic elds.