Regular Languages and Regular Expressions According to Our Definition, a Language Is Regular If There Exists a Finite State Auto
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Use Perl Regular Expressions in SAS® Shuguang Zhang, WRDS, Philadelphia, PA
NESUG 2007 Programming Beyond the Basics Use Perl Regular Expressions in SAS® Shuguang Zhang, WRDS, Philadelphia, PA ABSTRACT Regular Expression (Regexp) enhance search and replace operations on text. In SAS®, the INDEX, SCAN and SUBSTR functions along with concatenation (||) can be used for simple search and replace operations on static text. These functions lack flexibility and make searching dynamic text difficult, and involve more function calls. Regexp combines most, if not all, of these steps into one expression. This makes code less error prone, easier to maintain, clearer, and can improve performance. This paper will discuss three ways to use Perl Regular Expression in SAS: 1. Use SAS PRX functions; 2. Use Perl Regular Expression with filename statement through a PIPE such as ‘Filename fileref PIPE 'Perl programm'; 3. Use an X command such as ‘X Perl_program’; Three typical uses of regular expressions will also be discussed and example(s) will be presented for each: 1. Test for a pattern of characters within a string; 2. Replace text; 3. Extract a substring. INTRODUCTION Perl is short for “Practical Extraction and Report Language". Larry Wall Created Perl in mid-1980s when he was trying to produce some reports from a Usenet-Nes-like hierarchy of files. Perl tries to fill the gap between low-level programming and high-level programming and it is easy, nearly unlimited, and fast. A regular expression, often called a pattern in Perl, is a template that either matches or does not match a given string. That is, there are an infinite number of possible text strings. -

Lecture 18: Theory of Computation Regular Expressions and Dfas
Introduction to Theoretical CS Lecture 18: Theory of Computation Two fundamental questions. ! What can a computer do? ! What can a computer do with limited resources? General approach. Pentium IV running Linux kernel 2.4.22 ! Don't talk about specific machines or problems. ! Consider minimal abstract machines. ! Consider general classes of problems. COS126: General Computer Science • http://www.cs.Princeton.EDU/~cos126 2 Why Learn Theory In theory . Regular Expressions and DFAs ! Deeper understanding of what is a computer and computing. ! Foundation of all modern computers. ! Pure science. ! Philosophical implications. a* | (a*ba*ba*ba*)* In practice . ! Web search: theory of pattern matching. ! Sequential circuits: theory of finite state automata. a a a ! Compilers: theory of context free grammars. b b ! Cryptography: theory of computational complexity. 0 1 2 ! Data compression: theory of information. b "In theory there is no difference between theory and practice. In practice there is." -Yogi Berra 3 4 Pattern Matching Applications Regular Expressions: Basic Operations Test if a string matches some pattern. Regular expression. Notation to specify a set of strings. ! Process natural language. ! Scan for virus signatures. ! Search for information using Google. Operation Regular Expression Yes No ! Access information in digital libraries. ! Retrieve information from Lexis/Nexis. Concatenation aabaab aabaab every other string ! Search-and-replace in a word processors. cumulus succubus Wildcard .u.u.u. ! Filter text (spam, NetNanny, Carnivore, malware). jugulum tumultuous ! Validate data-entry fields (dates, email, URL, credit card). aa Union aa | baab baab every other string ! Search for markers in human genome using PROSITE patterns. aa ab Closure ab*a abbba ababa Parse text files. -

Midterm Study Sheet for CS3719 Regular Languages and Finite
Midterm study sheet for CS3719 Regular languages and finite automata: • An alphabet is a finite set of symbols. Set of all finite strings over an alphabet Σ is denoted Σ∗.A language is a subset of Σ∗. Empty string is called (epsilon). • Regular expressions are built recursively starting from ∅, and symbols from Σ and closing under ∗ Union (R1 ∪ R2), Concatenation (R1 ◦ R2) and Kleene Star (R denoting 0 or more repetitions of R) operations. These three operations are called regular operations. • A Deterministic Finite Automaton (DFA) D is a 5-tuple (Q, Σ, δ, q0,F ), where Q is a finite set of states, Σ is the alphabet, δ : Q × Σ → Q is the transition function, q0 is the start state, and F is the set of accept states. A DFA accepts a string if there exists a sequence of states starting with r0 = q0 and ending with rn ∈ F such that ∀i, 0 ≤ i < n, δ(ri, wi) = ri+1. The language of a DFA, denoted L(D) is the set of all and only strings that D accepts. • Deterministic finite automata are used in string matching algorithms such as Knuth-Morris-Pratt algorithm. • A language is called regular if it is recognized by some DFA. • ‘Theorem: The class of regular languages is closed under union, concatenation and Kleene star operations. • A non-deterministic finite automaton (NFA) is a 5-tuple (Q, Σ, δ, q0,F ), where Q, Σ, q0 and F are as in the case of DFA, but the transition function δ is δ : Q × (Σ ∪ {}) → P(Q). -

Chapter 6 Formal Language Theory
Chapter 6 Formal Language Theory In this chapter, we introduce formal language theory, the computational theories of languages and grammars. The models are actually inspired by formal logic, enriched with insights from the theory of computation. We begin with the definition of a language and then proceed to a rough characterization of the basic Chomsky hierarchy. We then turn to a more de- tailed consideration of the types of languages in the hierarchy and automata theory. 6.1 Languages What is a language? Formally, a language L is defined as as set (possibly infinite) of strings over some finite alphabet. Definition 7 (Language) A language L is a possibly infinite set of strings over a finite alphabet Σ. We define Σ∗ as the set of all possible strings over some alphabet Σ. Thus L ⊆ Σ∗. The set of all possible languages over some alphabet Σ is the set of ∗ all possible subsets of Σ∗, i.e. 2Σ or ℘(Σ∗). This may seem rather simple, but is actually perfectly adequate for our purposes. 6.2 Grammars A grammar is a way to characterize a language L, a way to list out which strings of Σ∗ are in L and which are not. If L is finite, we could simply list 94 CHAPTER 6. FORMAL LANGUAGE THEORY 95 the strings, but languages by definition need not be finite. In fact, all of the languages we are interested in are infinite. This is, as we showed in chapter 2, also true of human language. Relating the material of this chapter to that of the preceding two, we can view a grammar as a logical system by which we can prove things. -
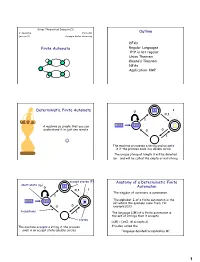
Deterministic Finite Automata 0 0,1 1
Great Theoretical Ideas in CS V. Adamchik CS 15-251 Outline Lecture 21 Carnegie Mellon University DFAs Finite Automata Regular Languages 0n1n is not regular Union Theorem Kleene’s Theorem NFAs Application: KMP 11 1 Deterministic Finite Automata 0 0,1 1 A machine so simple that you can 0111 111 1 ϵ understand it in just one minute 0 0 1 The machine processes a string and accepts it if the process ends in a double circle The unique string of length 0 will be denoted by ε and will be called the empty or null string accept states (F) Anatomy of a Deterministic Finite start state (q0) 11 0 Automaton 0,1 1 The singular of automata is automaton. 1 The alphabet Σ of a finite automaton is the 0111 111 1 ϵ set where the symbols come from, for 0 0 example {0,1} transitions 1 The language L(M) of a finite automaton is the set of strings that it accepts states L(M) = {x∈Σ: M accepts x} The machine accepts a string if the process It’s also called the ends in an accept state (double circle) “language decided/accepted by M”. 1 The Language L(M) of Machine M The Language L(M) of Machine M 0 0 0 0,1 1 q 0 q1 q0 1 1 What language does this DFA decide/accept? L(M) = All strings of 0s and 1s The language of a finite automaton is the set of strings that it accepts L(M) = { w | w has an even number of 1s} M = (Q, Σ, , q0, F) Q = {q0, q1, q2, q3} Formal definition of DFAs where Σ = {0,1} A finite automaton is a 5-tuple M = (Q, Σ, , q0, F) q0 Q is start state Q is the finite set of states F = {q1, q2} Q accept states : Q Σ → Q transition function Σ is the alphabet : Q Σ → Q is the transition function q 1 0 1 0 1 0,1 q0 Q is the start state q0 q0 q1 1 q q1 q2 q2 F Q is the set of accept states 0 M q2 0 0 q2 q3 q2 q q q 1 3 0 2 L(M) = the language of machine M q3 = set of all strings machine M accepts EXAMPLE Determine the language An automaton that accepts all recognized by and only those strings that contain 001 1 0,1 0,1 0 1 0 0 0 1 {0} {00} {001} 1 L(M)={1,11,111, …} 2 Membership problem Determine the language decided by Determine whether some word belongs to the language. -

Perl Regular Expressions Tip Sheet Functions and Call Routines
– Perl Regular Expressions Tip Sheet Functions and Call Routines Basic Syntax Advanced Syntax regex-id = prxparse(perl-regex) Character Behavior Character Behavior Compile Perl regular expression perl-regex and /…/ Starting and ending regex delimiters non-meta Match character return regex-id to be used by other PRX functions. | Alternation character () Grouping {}[]()^ Metacharacters, to match these pos = prxmatch(regex-id | perl-regex, source) $.|*+?\ characters, override (escape) with \ Search in source and return position of match or zero Wildcards/Character Class Shorthands \ Override (escape) next metacharacter if no match is found. Character Behavior \n Match capture buffer n Match any one character . (?:…) Non-capturing group new-string = prxchange(regex-id | perl-regex, times, \w Match a word character (alphanumeric old-string) plus "_") Lazy Repetition Factors Search and replace times number of times in old- \W Match a non-word character (match minimum number of times possible) string and return modified string in new-string. \s Match a whitespace character Character Behavior \S Match a non-whitespace character *? Match 0 or more times call prxchange(regex-id, times, old-string, new- \d Match a digit character +? Match 1 or more times string, res-length, trunc-value, num-of-changes) Match a non-digit character ?? Match 0 or 1 time Same as prior example and place length of result in \D {n}? Match exactly n times res-length, if result is too long to fit into new-string, Character Classes Match at least n times trunc-value is set to 1, and the number of changes is {n,}? Character Behavior Match at least n but not more than m placed in num-of-changes. -
6.045 Final Exam Name
6.045J/18.400J: Automata, Computability and Complexity Prof. Nancy Lynch 6.045 Final Exam May 20, 2005 Name: • Please write your name on each page. • This exam is open book, open notes. • There are two sheets of scratch paper at the end of this exam. • Questions vary substantially in difficulty. Use your time accordingly. • If you cannot produce a full proof, clearly state partial results for partial credit. • Good luck! Part Problem Points Grade Part I 1–10 50 1 20 2 15 3 25 Part II 4 15 5 15 6 10 Total 150 final-1 Name: Part I Multiple Choice Questions. (50 points, 5 points for each question) For each question, any number of the listed answersClearly may place be correct. an “X” in the box next to each of the answers that you are selecting. Problem 1: Which of the following are true statements about regular and nonregular languages? (All lan guages are over the alphabet{0, 1}) IfL1 ⊆ L2 andL2 is regular, thenL1 must be regular. IfL1 andL2 are nonregular, thenL1 ∪ L2 must be nonregular. IfL1 is nonregular, then the complementL 1 must of also be nonregular. IfL1 is regular,L2 is nonregular, andL1 ∩ L2 is nonregular, thenL1 ∪ L2 must be nonregular. IfL1 is regular,L2 is nonregular, andL1 ∩ L2 is regular, thenL1 ∪ L2 must be nonregular. Problem 2: Which of the following are guaranteed to be regular languages ? ∗ L2 = {ww : w ∈{0, 1}}. L2 = {ww : w ∈ L1}, whereL1 is a regular language. L2 = {w : ww ∈ L1}, whereL1 is a regular language. L2 = {w : for somex,| w| = |x| andwx ∈ L1}, whereL1 is a regular language. -

Unicode Regular Expressions Technical Reports
7/1/2019 UTS #18: Unicode Regular Expressions Technical Reports Working Draft for Proposed Update Unicode® Technical Standard #18 UNICODE REGULAR EXPRESSIONS Version 20 Editors Mark Davis, Andy Heninger Date 2019-07-01 This Version http://www.unicode.org/reports/tr18/tr18-20.html Previous Version http://www.unicode.org/reports/tr18/tr18-19.html Latest Version http://www.unicode.org/reports/tr18/ Latest Proposed http://www.unicode.org/reports/tr18/proposed.html Update Revision 20 Summary This document describes guidelines for how to adapt regular expression engines to use Unicode. Status This is a draft document which may be updated, replaced, or superseded by other documents at any time. Publication does not imply endorsement by the Unicode Consortium. This is not a stable document; it is inappropriate to cite this document as other than a work in progress. A Unicode Technical Standard (UTS) is an independent specification. Conformance to the Unicode Standard does not imply conformance to any UTS. Please submit corrigenda and other comments with the online reporting form [Feedback]. Related information that is useful in understanding this document is found in the References. For the latest version of the Unicode Standard, see [Unicode]. For a list of current Unicode Technical Reports, see [Reports]. For more information about versions of the Unicode Standard, see [Versions]. Contents 0 Introduction 0.1 Notation 0.2 Conformance 1 Basic Unicode Support: Level 1 1.1 Hex Notation 1.1.1 Hex Notation and Normalization 1.2 Properties 1.2.1 General -

Regular Expressions with a Brief Intro to FSM
Regular Expressions with a brief intro to FSM 15-123 Systems Skills in C and Unix Case for regular expressions • Many web applications require pattern matching – look for <a href> tag for links – Token search • A regular expression – A pattern that defines a class of strings – Special syntax used to represent the class • Eg; *.c - any pattern that ends with .c Formal Languages • Formal language consists of – An alphabet – Formal grammar • Formal grammar defines – Strings that belong to language • Formal languages with formal semantics generates rules for semantic specifications of programming languages Automaton • An automaton ( or automata in plural) is a machine that can recognize valid strings generated by a formal language . • A finite automata is a mathematical model of a finite state machine (FSM), an abstract model under which all modern computers are built. Automaton • A FSM is a machine that consists of a set of finite states and a transition table. • The FSM can be in any one of the states and can transit from one state to another based on a series of rules given by a transition function. Example What does this machine represents? Describe the kind of strings it will accept. Exercise • Draw a FSM that accepts any string with even number of A’s. Assume the alphabet is {A,B} Build a FSM • Stream: “I love cats and more cats and big cats ” • Pattern: “cat” Regular Expressions Regex versus FSM • A regular expressions and FSM’s are equivalent concepts. • Regular expression is a pattern that can be recognized by a FSM. • Regex is an example of how good theory leads to good programs Regular Expression • regex defines a class of patterns – Patterns that ends with a “*” • Regex utilities in unix – grep , awk , sed • Applications – Pattern matching (DNA) – Web searches Regex Engine • A software that can process a string to find regex matches. -

Regular Expressions
CS 172: Computability and Complexity Regular Expressions Sanjit A. Seshia EECS, UC Berkeley Acknowledgments: L.von Ahn, L. Blum, M. Blum The Picture So Far DFA NFA Regular language S. A. Seshia 2 Today’s Lecture DFA NFA Regular Regular language expression S. A. Seshia 3 Regular Expressions • What is a regular expression? S. A. Seshia 4 Regular Expressions • Q. What is a regular expression? • A. It’s a “textual”/ “algebraic” representation of a regular language – A DFA can be viewed as a “pictorial” / “explicit” representation • We will prove that a regular expressions (regexps) indeed represent regular languages S. A. Seshia 5 Regular Expressions: Definition σ is a regular expression representing { σσσ} ( σσσ ∈∈∈ ΣΣΣ ) ε is a regular expression representing { ε} ∅ is a regular expression representing ∅∅∅ If R 1 and R 2 are regular expressions representing L 1 and L 2 then: (R 1R2) represents L 1⋅⋅⋅L2 (R 1 ∪∪∪ R2) represents L 1 ∪∪∪ L2 (R 1)* represents L 1* S. A. Seshia 6 Operator Precedence 1. *** 2. ( often left out; ⋅⋅⋅ a ··· b ab ) 3. ∪∪∪ S. A. Seshia 7 Example of Precedence R1*R 2 ∪∪∪ R3 = ( ())R1* R2 ∪∪∪ R3 S. A. Seshia 8 What’s the regexp? { w | w has exactly a single 1 } 0*10* S. A. Seshia 9 What language does ∅∅∅* represent? {ε} S. A. Seshia 10 What’s the regexp? { w | w has length ≥ 3 and its 3rd symbol is 0 } ΣΣΣ2 0 ΣΣΣ* Σ = (0 ∪∪∪ 1) S. A. Seshia 11 Some Identities Let R, S, T be regular expressions • R ∪∪∪∅∅∅ = ? • R ···∅∅∅ = ? • Prove: R ( S ∪∪∪ T ) = R S ∪∪∪ R T (what’s the proof idea?) S. -

Context-Free Grammar for the Syntax of Regular Expression Over the ASCII
Context-free Grammar for the syntax of regular expression over the ASCII character set assumption : • A regular expression is to be interpreted a Haskell string, then is used to match against a Haskell string. Therefore, each regexp is enclosed inside a pair of double quotes, just like any Haskell string. For clarity, a regexp is highlighted and a “Haskell input string” is quoted for the examples in this document. • Since ASCII character strings will be encoded as in Haskell, therefore special control ASCII characters such as NUL and DEL are handled by Haskell. context-free grammar : BNF notation is used to describe the syntax of regular expressions defined in this document, with the following basic rules: • <nonterminal> ::= choice1 | choice2 | ... • Double quotes are used when necessary to reflect the literal meaning of the content itself. <regexp> ::= <union> | <concat> <union> ::= <regexp> "|" <concat> <concat> ::= <term><concat> | <term> <term> ::= <star> | <element> <star> ::= <element>* <element> ::= <group> | <char> | <emptySet> | <emptyStr> <group> ::= (<regexp>) <char> ::= <alphanum> | <symbol> | <white> <alphanum> ::= A | B | C | ... | Z | a | b | c | ... | z | 0 | 1 | 2 | ... | 9 <symbol> ::= ! | " | # | $ | % | & | ' | + | , | - | . | / | : | ; | < | = | > | ? | @ | [ | ] | ^ | _ | ` | { | } | ~ | <sp> | \<metachar> <sp> ::= " " <metachar> ::= \ | "|" | ( | ) | * | <white> <white> ::= <tab> | <vtab> | <nline> <tab> ::= \t <vtab> ::= \v <nline> ::= \n <emptySet> ::= Ø <emptyStr> ::= "" Explanations : 1. Definition of <metachar> in our definition of regexp: Symbol meaning \ Used to escape a metacharacter, \* means the star char itself | Specifies alternatives, y|n|m means y OR n OR m (...) Used for grouping, giving the group priority * Used to indicate zero or more of a regexp, a* matches the empty string, “a”, “aa”, “aaa” and so on Whi tespace char meaning \n A new line character \t A horizontal tab character \v A vertical tab character 2. -

PHP Regular Expressions
PHP Regular Expressions What is Regular Expression Regular Expressions, commonly known as "regex" or "RegExp", are a specially formatted text strings used to find patterns in text. Regular expressions are one of the most powerful tools available today for effective and efficient text processing and manipulations. For example, it can be used to verify whether the format of data i.e. name, email, phone number, etc. entered by the user was correct or not, find or replace matching string within text content, and so on. PHP (version 5.3 and above) supports Perl style regular expressions via its preg_ family of functions. Why Perl style regular expressions? Because Perl (Practical Extraction and Report Language) was the first mainstream programming language that provided integrated support for regular expressions and it is well known for its strong support of regular expressions and its extraordinary text processing and manipulation capabilities. Let's begin with a brief overview of the commonly used PHP's built-in pattern- matching functions before delving deep into the world of regular expressions. Function What it Does preg_match() Perform a regular expression match. preg_match_all() Perform a global regular expression match. preg_replace() Perform a regular expression search and replace. preg_grep() Returns the elements of the input array that matched the pattern. preg_split() Splits up a string into substrings using a regular expression. preg_quote() Quote regular expression characters found within a string. Note: The PHP preg_match() function stops searching after it finds the first match, whereas the preg_match_all() function continues searching until the end of the string and find all possible matches instead of stopping at the first match.