MEAN-VARIANCE PORTFOLIO OPTIMIZATION WHEN MEANS and COVARIANCES ARE UNKNOWN by Tze Leung Lai Haipeng Xing Zehao Chen Technical R
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
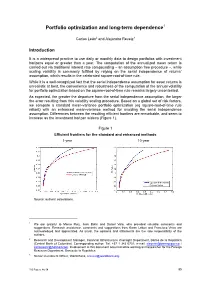
Portfolio Optimization and Long-Term Dependence1
Portfolio optimization and long-term dependence1 Carlos León2 and Alejandro Reveiz3 Introduction It is a widespread practice to use daily or monthly data to design portfolios with investment horizons equal or greater than a year. The computation of the annualized mean return is carried out via traditional interest rate compounding – an assumption free procedure –, while scaling volatility is commonly fulfilled by relying on the serial independence of returns’ assumption, which results in the celebrated square-root-of-time rule. While it is a well-recognized fact that the serial independence assumption for asset returns is unrealistic at best, the convenience and robustness of the computation of the annual volatility for portfolio optimization based on the square-root-of-time rule remains largely uncontested. As expected, the greater the departure from the serial independence assumption, the larger the error resulting from this volatility scaling procedure. Based on a global set of risk factors, we compare a standard mean-variance portfolio optimization (eg square-root-of-time rule reliant) with an enhanced mean-variance method for avoiding the serial independence assumption. Differences between the resulting efficient frontiers are remarkable, and seem to increase as the investment horizon widens (Figure 1). Figure 1 Efficient frontiers for the standard and enhanced methods 1-year 10-year Source: authors’ calculations. 1 We are grateful to Marco Ruíz, Jack Bohn and Daniel Vela, who provided valuable comments and suggestions. Research assistance, comments and suggestions from Karen Leiton and Francisco Vivas are acknowledged and appreciated. As usual, the opinions and statements are the sole responsibility of the authors. -

A Multi-Objective Approach to Portfolio Optimization
Rose-Hulman Undergraduate Mathematics Journal Volume 8 Issue 1 Article 12 A Multi-Objective Approach to Portfolio Optimization Yaoyao Clare Duan Boston College, [email protected] Follow this and additional works at: https://scholar.rose-hulman.edu/rhumj Recommended Citation Duan, Yaoyao Clare (2007) "A Multi-Objective Approach to Portfolio Optimization," Rose-Hulman Undergraduate Mathematics Journal: Vol. 8 : Iss. 1 , Article 12. Available at: https://scholar.rose-hulman.edu/rhumj/vol8/iss1/12 A Multi-objective Approach to Portfolio Optimization Yaoyao Clare Duan, Boston College, Chestnut Hill, MA Abstract: Optimization models play a critical role in determining portfolio strategies for investors. The traditional mean variance optimization approach has only one objective, which fails to meet the demand of investors who have multiple investment objectives. This paper presents a multi- objective approach to portfolio optimization problems. The proposed optimization model simultaneously optimizes portfolio risk and returns for investors and integrates various portfolio optimization models. Optimal portfolio strategy is produced for investors of various risk tolerance. Detailed analysis based on convex optimization and application of the model are provided and compared to the mean variance approach. 1. Introduction to Portfolio Optimization Portfolio optimization plays a critical role in determining portfolio strategies for investors. What investors hope to achieve from portfolio optimization is to maximize portfolio returns and minimize portfolio risk. Since return is compensated based on risk, investors have to balance the risk-return tradeoff for their investments. Therefore, there is no a single optimized portfolio that can satisfy all investors. An optimal portfolio is determined by an investor’s risk-return preference. -

Achieving Portfolio Diversification for Individuals with Low Financial
sustainability Article Achieving Portfolio Diversification for Individuals with Low Financial Sustainability Yongjae Lee 1 , Woo Chang Kim 2 and Jang Ho Kim 3,* 1 Department of Industrial Engineering, Ulsan National Institute of Science and Technology (UNIST), Ulsan 44919, Korea; [email protected] 2 Department of Industrial and Systems Engineering, Korea Advanced Institute of Science and Technology (KAIST), Daejeon 34141, Korea; [email protected] 3 Department of Industrial and Management Systems Engineering, Kyung Hee University, Yongin-si 17104, Gyeonggi-do, Korea * Correspondence: [email protected] Received: 5 August 2020; Accepted: 26 August 2020; Published: 30 August 2020 Abstract: While many individuals make investments to gain financial stability, most individual investors hold under-diversified portfolios that consist of only a few financial assets. Lack of diversification is alarming especially for average individuals because it may result in massive drawdowns in their portfolio returns. In this study, we analyze if it is theoretically feasible to construct fully risk-diversified portfolios even for the small accounts of not-so-rich individuals. In this regard, we formulate an investment size constrained mean-variance portfolio selection problem and investigate the relationship between the investment amount and diversification effect. Keywords: portfolio size; portfolio diversification; individual investor; financial sustainability 1. Introduction Achieving financial sustainability is a basic goal for everyone and it has become a shared concern globally due to increasing life expectancy. Low financial sustainability may refer to individuals with low financial wealth, as well as investors with a lack of financial literacy. Especially for individuals with limited wealth, financial sustainability after retirement is a real concern because of uncertainty in pension plans arising from relatively early retirement age and change in the demographic structure (see, for example, [1,2]). -

Optimization of Conditional Value-At-Risk
Implemented in Portfolio Safeguard by AORDA.com Optimization of conditional value-at-risk R. Tyrrell Rockafellar Department of Applied Mathematics, University of Washington, 408 L Guggenheim Hall, Box 352420, Seattle, Washington 98195-2420, USA Stanislav Uryasev Department of Industrial and Systems Engineering, University of Florida, PO Box 116595, 303 Weil Hall, Gainesville, Florida 32611-6595, USA A new approach to optimizing or hedging a portfolio of ®nancial instruments to reduce risk is presented and tested on applications. It focuses on minimizing conditional value-at-risk CVaR) rather than minimizing value-at-risk VaR),but portfolios with low CVaR necessarily have low VaR as well. CVaR,also called mean excess loss,mean shortfall,or tail VaR,is in any case considered to be a more consistent measure of risk than VaR. Central to the new approach is a technique for portfolio optimization which calculates VaR and optimizes CVaR simultaneously. This technique is suitable for use by investment companies,brokerage ®rms,mutual funds, and any business that evaluates risk. It can be combined with analytical or scenario- based methods to optimize portfolios with large numbers of instruments,in which case the calculations often come down to linear programming or nonsmooth programming. The methodology can also be applied to the optimization of percentiles in contexts outside of ®nance. 1. INTRODUCTION This paper introduces a new approach to optimizing a portfolio so as to reduce the risk of high losses. Value-at-risk VaR) has a role in the approach, but the emphasis is on conditional value-at-risk CVaR), which is also known as mean excess loss, mean shortfall, or tail VaR. -

Portfolio Optimization
PORTFOLIO OPTIMIZATION BY RENI~ SCHNIEPER Zurich hlsurance Company, Reinsurance KEYWORDS Reinsurance, retentions, non linear optimization, insurance risk, financial risk, Markowitz's portfolio selection method, CAPM. ABSTRACT Based on the profit and loss account of an insurance company we derive a probabilistic model for the financial result of the company, thereby both assets and liabilities are marked to market. We thus focus o11 the economic value of the company. We first analyse the underwriting risk of the company. The maximization of the risk return ratio of the company is derived as optimality criterion. It is shown how the risk return ratio of heterogeneous portfolios or of catastrophe exposed portfolios can be dramatically improved through reinsurance. The improvement of the risk return ratio through portfolio diversification is also analysed. In section 3 of the paper we analyse the loss reserve risk of the company. It is shown that this risk consists of a loss reserve development risk and of a yield curve risk which stems from the discounting of the loss reserves. This latter risk can be fully hedged through asset liability matching. In section 4 we derive our general model. The portfolio of the company consists of a portfolio of insurance risks and of a portfolio of financial risks. Our model allows for a silnultaneous optimization of both portfolios of risks. A theorem is derived which gives the optimal retention policy of the company together with its optimal asset allocation. Some of the material presented in this paper is taken from Schnieper, 1997. It has been repeated here in order to make this article self contained. -

Heuristic Approaches to Portfolio Optimization by Abubakar Yahaya
Heuristic Approaches to Portfolio Optimization by Abubakar Yahaya BSc (Statistics) Usmanu Danfodiyo University, Sokoto, Nigeria. MSc (Decision Modelling & Information Systems), Brunei University, UK. This thesis is submitted for the award of degree of Doctor of Philosophy in the Department of Management Science, Lancaster University Management School December 2010. ProQuest Number: 11003476 All rights reserved INFORMATION TO ALL USERS The quality of this reproduction is dependent upon the quality of the copy submitted. In the unlikely event that the author did not send a com plete manuscript and there are missing pages, these will be noted. Also, if material had to be removed, a note will indicate the deletion. uest ProQuest 11003476 Published by ProQuest LLC(2018). Copyright of the Dissertation is held by the Author. All rights reserved. This work is protected against unauthorized copying under Title 17, United States C ode Microform Edition © ProQuest LLC. ProQuest LLC. 789 East Eisenhower Parkway P.O. Box 1346 Ann Arbor, Ml 48106- 1346 LANCASTER 11 ' - Dedication To My lovely and caring wife: Amina My beautiful and lovely daughter: Fatima. My gorgeous sons: Muhammad, Ahmad and (my little Lancastrian) Al-Ameen. Page 2 of 277 LANCASTER Acknowledgement All praises and thanks are due to Almighty Allah (TWT), the LORD of all the seven heavens and earths alike. He is the LORD of whatever is contained therein. I praise Him, thank Him and ask for His forgiveness over all my sins and shortcomings. He is the provider of all provisions and sustenance to all living things. It is in the Name of such Allah (TWT), I begin to write this thesis. -

Practical Portfolio Optimization
Practical Portfolio Optimization K V Fernando NAG Ltd Wilkinson House Jordan Hill Oxford OX2 8DR United Kingdom email:[email protected] i Abstract NAG Libraries have many powerful and reliable optimizers which can be used to solve large portfolio optimization and selection problems in the financial industry. These versatile routines are also suitable for academic research and teaching. Key words Markowitz, mean-variance analysis, optimal portfolios, minimum variance portfolio, portfolio selection, portfolio allocation, portfolio diversification, portfolio optimization, efficient frontier, mean-variance frontier, MV efficiency ii Contents 1 Introduction 1 2 NAG Routines for Optimization 2 2.1ASelectionofLibraryRoutines................. 2 2.2 Quadratic Programming with Linear Constraints . 3 2.3NonlinearProgramming..................... 3 2.4RoutinesforSparseMatrixProblems.............. 3 2.5ForwardandReverseCommunication............. 4 2.6 Hardware, Operating Systems and Environments . 4 3InterfacestoRoutines 4 3.1PortfolioWeights......................... 4 3.2PrimaryData........................... 4 3.3GeneralLinearConstraints................... 5 3.4NonlinearConstraints...................... 6 3.5ColdandWarmStarts...................... 6 4 The Optimization Problems 6 5 Processing of Raw Data 7 5.1TheCovarianceMatrixinFactoredForm........... 7 5.2 Determination of the Singular Values of the Cholesky Factors 9 5.3IftheCovarianceMatrixAlreadyExists............ 9 5.4EigenvaluesoftheCovarianceMatrix.............. 10 5.5MissingValues......................... -

Portfolio Optimization: Thinking Outside the Style Box
Portfolio Optimization: Thinking Outside the Style Box Asset Allocation, Portfolio Optimization and Optimization Through Hedged Equity By Micah Wakefield, CAIA®, AAMS®, AWMA® February 23, 2017 February 2017 Portfolio Optimization Thinking Outside the Style Box - 2 CONTENTS Revisions 3 Objectives 4 Portfolio Optimization 5 An Alternative Approach to Portfolio Optimization 10 Portfolio Improvement through Hedged Assets 12 Specific Asset Comparisons for Use in Alternative Portfolio Optimization 16 The Defined Risk Portfolio 18 Swan Global Investments | 970-382-8901 | swanglobalinvestments.com February 2017 Portfolio Optimization Thinking Outside the Style Box - 3 REVISIONS A. Initial Release January 31, 2015 Micah J. Wakefield, AWMA®, AAMS® Director of Research and Product Development Swan Global Investments B. Second Release October 1, 2016 Micah J. Wakefield, CAIA®, AWMA®, AAMS® Director of Research and Product Development Swan Global Investments C. Third Release February 23, 2017 Micah J. Wakefield, CAIA®, AWMA®, AAMS® Director of Research and Product Development Swan Global Investments Swan Global Investments | 970-382-8901 | swanglobalinvestments.com February 2017 Portfolio Optimization Thinking Outside the Style Box - 4 OBJECTIVES Swan is focused on helping provide financial advisors with the thought leadership necessary to differentiate themselves and make their businesses stronger and more valuable. The purpose of this document is to highlight our theoretical view that a diversified hedged assets portfolio is a more effective and -

Elements of Financial Engineering Course
Baruch-NSD_Summer2019-Lec4-ModernPortfolioTheory http://localhost:8888/nbconvert/html/Google Drive/Lectures/Ba... Elements of Financial Engineering Course Baruch-NSD Summer Camp 2019 Lecture 4: Modern Portfolio Theory and CAPM Tai-Ho Wang (王 太 和) Outline of the lecture Modern portfolio theory and the Markowitz model Capital asset pricing model (CAPM) Arbitrage pricing theory (APT) Fama-French 3-factor model Black-Litterman model Merton's problem Harry Markowitz From the Wikipage (https://en.wikipedia.org/wiki/Harry_Markowitz) in Wikipedia: Markowitz won the Nobel Memorial Prize in Economic Sciences in 1990 while a professor of finance at Baruch College of the City University of New York. In the preceding year, he received the John von Neumann Theory Prize from the Operations Research Society of America (now Institute for Operations Research and the Management Sciences, INFORMS) for his contributions in the theory of three fields: portfolio theory; sparse matrix methods; and simulation language programming (SIMSCRIPT). Extensions From Wikipedia: Since MPT's introduction in 1952, many attempts have been made to improve the model, especially by using more realistic assumptions. Post-modern portfolio theory extends MPT by adopting non-normally distributed, asymmetric, and fat-tailed measures of risk. This helps with some of these problems, but not others. Black-Litterman model optimization is an extension of unconstrained Markowitz optimization that incorporates relative and absolute 'views' on inputs of risk and returns from financial experts. With the advances in Artificial Intelligence, other information such as market sentiment and financial knowledge can be incorporated automatically to the 'views'. 1 of 31 8/13/19, 8:21 PM Baruch-NSD_Summer2019-Lec4-ModernPortfolioTheory http://localhost:8888/nbconvert/html/Google Drive/Lectures/Ba.. -

Risk Management and Portfolio Optimization for Volatile Markets
Risk Management and Portfolio Optimization for Volatile Markets Svetlozar T. Rachev Chief Scientist, FinAnalytica and Chair Professor of Statistics, Econometrics and Mathematical Finance, School of Economics and Business Engineering, University of Karlsruhe Borjana Racheva-Iotova Vice President and Managing Director of Research and Development, FinAnalytica Stoyan V. Stoyanov Chief Financial Researcher, FinAnalytica Frank J. Fabozzi Yale University, School of Management Abstract We describe a framework of a system for risk estimation and portfolio optimization based on stable distributions and the average value-at-risk risk measure. In contrast to normal distributions, stable distributions capture the fat tails and the asymmetric nature of real-world risk factor distributions. In addition, we make use of copulas, a generalization of overly restrictive linear correlation models, to account for the dependencies between risk factors during extreme events. Using superior models, VaR becomes a much more accurate measure of downside risk. More importantly Stable Expected Tail Loss (SETL) can be accurately calculated and used as a more informative risk measure. Along with being a superior risk measure, SETL enables an elegant approach to risk budgeting and portfolio optimization Finally, we mention alternative investment performance measurement tools. 1. Introduction The two main conventional approaches to modeling asset returns are based either on a historical or a normal (Gaussian) distribution for returns. Neither approach adequately captures unusual behavior of asset prices and returns. The historical model is bounded by the extent of the available observations and the normal distribution model inherently cannot produce extreme returns. The inadequacy of the normal distribution is well recognized by the risk management community. -

A Mean-Variance-Skewness Portfolio Optimization Model
Journal of the Operations Research © 1995 The Operations Research Society of Japan Society of Japan VoJ. 38, No. 2, June 1995 A MEAN-VARIANCE-SKI<~WNESS PORTFOLIO OPTIMIZATION MODEL Hiroshi Konno Ken-ichi Suzuki Tokyo Institute of Technology (Received May 10, 1993; Revised January 26, 1994) Abstract We will propose a mean-variance-skewness(MVS) portfolio optimization model, a direct exten sion of the classical mean-variance model to the situation where the skewness of the rate of return of assets and the third order derivative of a utility function play significant roles in choosing an optimal portfolio. The MVS model enables one to calculate an approximate mean-variance-skewness efficient surface, by which one can compute a portfolio with maximal expected utility for any decreasingly risk averse utility functions. Also, we propose three computational schemes for solving an associated nonconcave maximization problem, and some preliminary computational results will be reported. 1. Introduction In [12], the authors proposed a mean-absolute deviation-skewness (MADS) portfolio opti mization model, in which the lower semi-third moment of the rate of return of a portfolio is maximized subject to constraints on the mean and the absolute deviation of the rate of return. This model is an extension of the standard Mean-Variance (MV) model developed by H. Markowitz [18J, and is motivated by observations on the distribution of stock data in the market and on the practitioners' perception against risk. The standard MV model is based upon the assumptions that an investor is risk averse and that either (i) the distribution of the rate of return is multi-variate normal, or (ii) the utility of the investor is a quadratic function of the rate of return. -

Modern Portfolio Theory & Quadratic Programming
Honor’s Thesis: Portfolio Construction & Modern Portfolio Theory Marinella Piñate B.S. in Industrial and Systems Engineering Graduation Term: Fall 2013 Honor’s Status: Magna Cum Laude & Oscar Oropeza B.S. in Industrial and Systems Engineering Graduation Term: Fall 2013 Honor’s Status: Magna Cum Laude Table of Contents Abstract ......................................................................................................................................................... 2 Introduction ................................................................................................................................................... 2 Investment Management ............................................................................................................................... 3 Portfolio Selection and the Markowitz Model .............................................................................................. 4 Model Inputs ............................................................................................................................................. 7 Model Limitations ..................................................................................................................................... 7 Alternatives to the Markowitz Model ....................................................................................................... 8 Asset Allocation vs. Equity Portfolio Optimization ................................................................................. 9 Methodology ................................................................................................................................................