Static and Dynamic Portfolio Allocation with Nonstandard Utility Functions
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Portfolio Selection Under Exponential and Quadratic Utility
Portfolio Selection Under Exponential and Quadratic Utility Steven T. Buccola The production or marketing portfolio that is optimal under the assumption of quadratic utility may or may not be optimal under the assumption of exponential utility. In certain cases, the necessary and sufficient condition for an identical solution is that absolute risk aversion coefficients associated with the two utility functions be the same. In other cases, equality of risk aversion coefficients is a sufficient condition only. A comparison is made between use of exponential and quadratic utility in the analysis of a California farmer's marketing problem. A large number of utility functional forms difference. Under other conditions, the have been proposed for use in selecting opti- choice has a significant impact on optimal mal portfolios of risky prospects [Tsaing]. For behavior. purposes of both theoretical and applied eco- Suppose an analyst is studying a continu- nomic research, attention has primarily been ously divisible set of alternative production directed to the quadratic and exponential or marketing options offering approximately forms. After enjoying widespread use in the normally-distributed returns, and that he 1950s and 1960s, the quadratic form came wishes to select the portfolio of these options under criticism by Pratt and others and lost with highest expected utility. The analyst is much of its reputability. In contrast the expo- considering using an exponential utility func- nential form has become increasingly popu- tion U = -exp(-Xx), X > 0, or a quadratic lar, due in large measure to its mathematical utility function U = x -vx,v, > 0, x < /2v, tractability [Attanasi and Karlinger; O'Con- where U is utility and x is wealth. -
Portfolio Optimization and Long-Term Dependence1
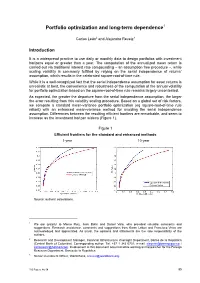
Portfolio optimization and long-term dependence1 Carlos León2 and Alejandro Reveiz3 Introduction It is a widespread practice to use daily or monthly data to design portfolios with investment horizons equal or greater than a year. The computation of the annualized mean return is carried out via traditional interest rate compounding – an assumption free procedure –, while scaling volatility is commonly fulfilled by relying on the serial independence of returns’ assumption, which results in the celebrated square-root-of-time rule. While it is a well-recognized fact that the serial independence assumption for asset returns is unrealistic at best, the convenience and robustness of the computation of the annual volatility for portfolio optimization based on the square-root-of-time rule remains largely uncontested. As expected, the greater the departure from the serial independence assumption, the larger the error resulting from this volatility scaling procedure. Based on a global set of risk factors, we compare a standard mean-variance portfolio optimization (eg square-root-of-time rule reliant) with an enhanced mean-variance method for avoiding the serial independence assumption. Differences between the resulting efficient frontiers are remarkable, and seem to increase as the investment horizon widens (Figure 1). Figure 1 Efficient frontiers for the standard and enhanced methods 1-year 10-year Source: authors’ calculations. 1 We are grateful to Marco Ruíz, Jack Bohn and Daniel Vela, who provided valuable comments and suggestions. Research assistance, comments and suggestions from Karen Leiton and Francisco Vivas are acknowledged and appreciated. As usual, the opinions and statements are the sole responsibility of the authors. -

Utility with Decreasing Risk Aversion
144 UTILITY WITH DECREASING RISK AVERSION GARY G. VENTER Abstract Utility theory is discussed as a basis for premium calculation. Desirable features of utility functions are enumerated, including decreasing absolute risk aversion. Examples are given of functions meeting this requirement. Calculating premiums for simplified risk situations is advanced as a step towards selecting a specific utility function. An example of a more typical portfolio pricing problem is included. “The large rattling dice exhilarate me as torrents borne on a precipice flowing in a desert. To the winning player they are tipped with honey, slaying hirri in return by taking away the gambler’s all. Giving serious attention to my advice, play not with dice: pursue agriculture: delight in wealth so acquired.” KAVASHA Rig Veda X.3:5 Avoidance of risk situations has been regarded as prudent throughout history, but individuals with a preference for risk are also known. For many decision makers, the value of different potential levels of wealth is apparently not strictly proportional to the wealth level itself. A mathematical device to treat this is the utility function, which assigns a value to each wealth level. Thus, a 50-50 chance at double or nothing on your wealth level may or may not be felt equivalent to maintaining your present level; however, a 50-50 chance at nothing or the value of wealth that would double your utility (if such a value existed) would be equivalent to maintaining the present level, assuming that the utility of zero wealth is zero. This is more or less by definition, as the utility function is set up to make such comparisons possible. -

The Case Against Power Utility and a Suggested Alternative: Resurrecting Exponential Utility
Munich Personal RePEc Archive The Case Against Power Utility and a Suggested Alternative: Resurrecting Exponential Utility Alpanda, Sami and Woglom, Geoffrey Amherst College, Amherst College July 2007 Online at https://mpra.ub.uni-muenchen.de/5897/ MPRA Paper No. 5897, posted 23 Nov 2007 06:09 UTC The Case against Power Utility and a Suggested Alternative: Resurrecting Exponential Utility Sami Alpanda Geoffrey Woglom Amherst College Amherst College Abstract Utility modeled as a power function is commonly used in the literature despite the fact that it is unbounded and generates asset pricing puzzles. The unboundedness property leads to St. Petersburg paradox issues and indifference to compound gambles, but these problems have largely been ignored. The asset pricing puzzles have been solved by introducing habit formation to the usual power utility. Given these issues, we believe it is time re-examine exponential utility. Exponential utility was abandoned largely because it implies increasing relative risk aversion in a cross-section of individuals and non- stationarity of the aggregate consumption to wealth ratio, contradicting macroeconomic data. We propose an alternative preference specification with exponential utility and relative habit formation. We show that this utility function is bounded, consistent with asset pricing facts, generates near-constant relative risk aversion in a cross-section of individuals and a stationary ratio of aggregate consumption to wealth. Keywords: unbounded utility, asset pricing puzzles, habit formation JEL Classification: D810, G110 1 1. Introduction Exponential utility functions have been mostly abandoned from economic theory despite their analytical convenience. On the other hand, power utility, which is also highly tractable, has become the workhorse of modern macroeconomics and asset pricing. -

Pareto Utility
Theory Dec. (2013) 75:43–57 DOI 10.1007/s11238-012-9293-8 Pareto utility Masako Ikefuji · Roger J. A. Laeven · Jan R. Magnus · Chris Muris Received: 2 September 2011 / Accepted: 3 January 2012 / Published online: 26 January 2012 © The Author(s) 2012. This article is published with open access at Springerlink.com Abstract In searching for an appropriate utility function in the expected utility framework, we formulate four properties that we want the utility function to satisfy. We conduct a search for such a function, and we identify Pareto utility as a func- tion satisfying all four desired properties. Pareto utility is a flexible yet simple and parsimonious two-parameter family. It exhibits decreasing absolute risk aversion and increasing but bounded relative risk aversion. It is applicable irrespective of the prob- ability distribution relevant to the prospect to be evaluated. Pareto utility is therefore particularly suited for catastrophic risk analysis. A new and related class of generalized exponential (gexpo) utility functions is also studied. This class is particularly relevant in situations where absolute risk tolerance is thought to be concave rather than linear. Keywords Parametric utility · Hyperbolic absolute risk aversion (HARA) · Exponential utility · Power utility M. Ikefuji Institute of Social and Economic Research, Osaka University, Osaka, Japan M. Ikefuji Department of Environmental and Business Economics, University of Southern Denmark, Esbjerg, Denmark e-mail: [email protected] R. J. A. Laeven (B) · J. R. Magnus Department of Econometrics & Operations Research, Tilburg University, Tilburg, The Netherlands e-mail: [email protected] J. R. Magnus e-mail: [email protected] C. -

A Multi-Objective Approach to Portfolio Optimization
Rose-Hulman Undergraduate Mathematics Journal Volume 8 Issue 1 Article 12 A Multi-Objective Approach to Portfolio Optimization Yaoyao Clare Duan Boston College, [email protected] Follow this and additional works at: https://scholar.rose-hulman.edu/rhumj Recommended Citation Duan, Yaoyao Clare (2007) "A Multi-Objective Approach to Portfolio Optimization," Rose-Hulman Undergraduate Mathematics Journal: Vol. 8 : Iss. 1 , Article 12. Available at: https://scholar.rose-hulman.edu/rhumj/vol8/iss1/12 A Multi-objective Approach to Portfolio Optimization Yaoyao Clare Duan, Boston College, Chestnut Hill, MA Abstract: Optimization models play a critical role in determining portfolio strategies for investors. The traditional mean variance optimization approach has only one objective, which fails to meet the demand of investors who have multiple investment objectives. This paper presents a multi- objective approach to portfolio optimization problems. The proposed optimization model simultaneously optimizes portfolio risk and returns for investors and integrates various portfolio optimization models. Optimal portfolio strategy is produced for investors of various risk tolerance. Detailed analysis based on convex optimization and application of the model are provided and compared to the mean variance approach. 1. Introduction to Portfolio Optimization Portfolio optimization plays a critical role in determining portfolio strategies for investors. What investors hope to achieve from portfolio optimization is to maximize portfolio returns and minimize portfolio risk. Since return is compensated based on risk, investors have to balance the risk-return tradeoff for their investments. Therefore, there is no a single optimized portfolio that can satisfy all investors. An optimal portfolio is determined by an investor’s risk-return preference. -

Achieving Portfolio Diversification for Individuals with Low Financial
sustainability Article Achieving Portfolio Diversification for Individuals with Low Financial Sustainability Yongjae Lee 1 , Woo Chang Kim 2 and Jang Ho Kim 3,* 1 Department of Industrial Engineering, Ulsan National Institute of Science and Technology (UNIST), Ulsan 44919, Korea; [email protected] 2 Department of Industrial and Systems Engineering, Korea Advanced Institute of Science and Technology (KAIST), Daejeon 34141, Korea; [email protected] 3 Department of Industrial and Management Systems Engineering, Kyung Hee University, Yongin-si 17104, Gyeonggi-do, Korea * Correspondence: [email protected] Received: 5 August 2020; Accepted: 26 August 2020; Published: 30 August 2020 Abstract: While many individuals make investments to gain financial stability, most individual investors hold under-diversified portfolios that consist of only a few financial assets. Lack of diversification is alarming especially for average individuals because it may result in massive drawdowns in their portfolio returns. In this study, we analyze if it is theoretically feasible to construct fully risk-diversified portfolios even for the small accounts of not-so-rich individuals. In this regard, we formulate an investment size constrained mean-variance portfolio selection problem and investigate the relationship between the investment amount and diversification effect. Keywords: portfolio size; portfolio diversification; individual investor; financial sustainability 1. Introduction Achieving financial sustainability is a basic goal for everyone and it has become a shared concern globally due to increasing life expectancy. Low financial sustainability may refer to individuals with low financial wealth, as well as investors with a lack of financial literacy. Especially for individuals with limited wealth, financial sustainability after retirement is a real concern because of uncertainty in pension plans arising from relatively early retirement age and change in the demographic structure (see, for example, [1,2]). -

Estimating Exponential Utility Functions
,~ j,;' I) ':;l) . G rio"". 0 • 0 (? _.0 o I') Q () l% a 9(;' o Q estimatiqg "ExPC?ttenti~1 ·:U····:t·····~·I·····I:·I·+u·· ;F;";;u::·:n6',.t5"'·;~:n·'.' ·s.. ·, .' ..., .'.: :','. ..•. ".. '..'. ;. ~':,,;'V~ ..' .'. o c:::::::> ' ,;", o o (b~s. ) EconOm:ics, .Statistics'·Oftd (OOfI,ati,tS /} o i_JS~~n;'~~t'~C:'T" " o .j o i) " (> C. "French " State Un I vers" I ty, and - ~~ ~ from Agric~ltur;al Economic Research, Janucrry 1978" \/01. 30, No. 1 ~~'~....' .. ' .. exponential.utility fun~tion for money has 10ng att:racted attentic;m fromAtheorists~~ because it exhibits\~oni"creasing absolute, risk aversion. j\lso, under certain con- ~ ditions, it generates an expected utility functi()n that is maximizable in a quadratic 1 program. However, "this "'functiona,l form presents 'estimation problems. Logarithmic • transformation of an exponential uti 1i,t,y, function does not conform to the Von Neumann Horgenste~ axioms. Hence', it cannot be used as ,.a basis for best fit in statistical analysis. A criterion is described that can be used to select a best-flt exponential uti 1ity.fun.ction, and its appl.ica,ti~!!c"",L~I.J~~~er utJ1ity an~,,~J~!s. is (~en~~~.~~r.~~ed ,~-».,.....'~\ ~ ....,.,." .,-~~ '1\, ~.... jt-~ .. -~..,q,·""·"~.""""11!"~""""'"""'\.'<'..".tft4._ ... 1' ,,''-,. < ~ i\ ,c,( ~--~""..-~,."".... .... ,~. '" ~. "~:"''''.jq''K>''''~~''l;:' ", " & ' (J 11' 1 i ,~ r.~ .... ' t ' .'~ >':J ~rr 1 C >J '¥ ~r ~1 f' if! 1 t::' ~ t,n t; ~,l IG " Canputerized simulation o Computers c Economic analysis Est imates 1\, Exponential functions " ~ogarlthm functions Risk ~Statistical analysis Utility routines 1711. IdenEifier./Open-Eaded Titnu (;:::; Absolute risk aversion Compute r app,l i cat i ens' Logari thmi c traosformatian Honey (/ Von Neumann-Morgenstern axioms )) ~ 12-A, 12-8 PB . -

Optimization of Conditional Value-At-Risk
Implemented in Portfolio Safeguard by AORDA.com Optimization of conditional value-at-risk R. Tyrrell Rockafellar Department of Applied Mathematics, University of Washington, 408 L Guggenheim Hall, Box 352420, Seattle, Washington 98195-2420, USA Stanislav Uryasev Department of Industrial and Systems Engineering, University of Florida, PO Box 116595, 303 Weil Hall, Gainesville, Florida 32611-6595, USA A new approach to optimizing or hedging a portfolio of ®nancial instruments to reduce risk is presented and tested on applications. It focuses on minimizing conditional value-at-risk CVaR) rather than minimizing value-at-risk VaR),but portfolios with low CVaR necessarily have low VaR as well. CVaR,also called mean excess loss,mean shortfall,or tail VaR,is in any case considered to be a more consistent measure of risk than VaR. Central to the new approach is a technique for portfolio optimization which calculates VaR and optimizes CVaR simultaneously. This technique is suitable for use by investment companies,brokerage ®rms,mutual funds, and any business that evaluates risk. It can be combined with analytical or scenario- based methods to optimize portfolios with large numbers of instruments,in which case the calculations often come down to linear programming or nonsmooth programming. The methodology can also be applied to the optimization of percentiles in contexts outside of ®nance. 1. INTRODUCTION This paper introduces a new approach to optimizing a portfolio so as to reduce the risk of high losses. Value-at-risk VaR) has a role in the approach, but the emphasis is on conditional value-at-risk CVaR), which is also known as mean excess loss, mean shortfall, or tail VaR. -

Portfolio Optimization
PORTFOLIO OPTIMIZATION BY RENI~ SCHNIEPER Zurich hlsurance Company, Reinsurance KEYWORDS Reinsurance, retentions, non linear optimization, insurance risk, financial risk, Markowitz's portfolio selection method, CAPM. ABSTRACT Based on the profit and loss account of an insurance company we derive a probabilistic model for the financial result of the company, thereby both assets and liabilities are marked to market. We thus focus o11 the economic value of the company. We first analyse the underwriting risk of the company. The maximization of the risk return ratio of the company is derived as optimality criterion. It is shown how the risk return ratio of heterogeneous portfolios or of catastrophe exposed portfolios can be dramatically improved through reinsurance. The improvement of the risk return ratio through portfolio diversification is also analysed. In section 3 of the paper we analyse the loss reserve risk of the company. It is shown that this risk consists of a loss reserve development risk and of a yield curve risk which stems from the discounting of the loss reserves. This latter risk can be fully hedged through asset liability matching. In section 4 we derive our general model. The portfolio of the company consists of a portfolio of insurance risks and of a portfolio of financial risks. Our model allows for a silnultaneous optimization of both portfolios of risks. A theorem is derived which gives the optimal retention policy of the company together with its optimal asset allocation. Some of the material presented in this paper is taken from Schnieper, 1997. It has been repeated here in order to make this article self contained. -

Heuristic Approaches to Portfolio Optimization by Abubakar Yahaya
Heuristic Approaches to Portfolio Optimization by Abubakar Yahaya BSc (Statistics) Usmanu Danfodiyo University, Sokoto, Nigeria. MSc (Decision Modelling & Information Systems), Brunei University, UK. This thesis is submitted for the award of degree of Doctor of Philosophy in the Department of Management Science, Lancaster University Management School December 2010. ProQuest Number: 11003476 All rights reserved INFORMATION TO ALL USERS The quality of this reproduction is dependent upon the quality of the copy submitted. In the unlikely event that the author did not send a com plete manuscript and there are missing pages, these will be noted. Also, if material had to be removed, a note will indicate the deletion. uest ProQuest 11003476 Published by ProQuest LLC(2018). Copyright of the Dissertation is held by the Author. All rights reserved. This work is protected against unauthorized copying under Title 17, United States C ode Microform Edition © ProQuest LLC. ProQuest LLC. 789 East Eisenhower Parkway P.O. Box 1346 Ann Arbor, Ml 48106- 1346 LANCASTER 11 ' - Dedication To My lovely and caring wife: Amina My beautiful and lovely daughter: Fatima. My gorgeous sons: Muhammad, Ahmad and (my little Lancastrian) Al-Ameen. Page 2 of 277 LANCASTER Acknowledgement All praises and thanks are due to Almighty Allah (TWT), the LORD of all the seven heavens and earths alike. He is the LORD of whatever is contained therein. I praise Him, thank Him and ask for His forgiveness over all my sins and shortcomings. He is the provider of all provisions and sustenance to all living things. It is in the Name of such Allah (TWT), I begin to write this thesis. -

Cardinal Sins: Utility Specification and the Measurement of Risk Aversion
19 Eisenhauer, International Journal of Applied Economics, 13(2), September 2016, 19-29 Cardinal Sins: Utility Specification and the Measurement of Risk Aversion Joseph G. Eisenhauer* University of Detroit Mercy ___________________________________________________________________________ Abstract: In contrast to the ideal of allowing empirical data to reveal individual preferences, economists have frequently resorted to constructing preference functions with convenient parameters and then using data merely to estimate the magnitude of the parameters. In particular, it has become common practice for researchers seeking to measure risk aversion to select an arbitrary utility specification and assume that the same functional form applies to all individuals in a given sample. This note illustrates the prevalence of this practice and how unreliable such an approach may be. Using a recently developed data set from Thailand, empirical results for the Pratt-Arrow coefficients of risk aversion are compared across isoelastic and exponential utility functions. The latter are estimated to be, on average, more than five times larger than the former, suggesting the possibility of enormous distortions in empirical studies that assume specific cardinal utility functions. Keywords: risk aversion, utility function, isoelastic, exponential, representative agent JEL Classification: D810 ___________________________________________________________________________ 1. Introduction Although utility is canonically described as an ordinal ranking of preferences over goods and services, economists have frequently adopted specific functional forms that yield cardinal measures (Barnett, 2003). As early as the 18th century, Bernoulli (1738) used a logarithmic utility function to illustrate the concept of the diminishing marginal utility of wealth in his explanation of risk aversion. This tendency has become increasingly prevalent since Pratt (1964) and Arrow (1965) introduced quantitative measures of risk aversion.