DOCSLIB.ORG

Optical Design with Zemax for Phd - Advanced

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Optical Design with Zemax for Phd - Advanced Optical Design with Zemax for PhD - Advanced Seminar 8 : Tolerancing II 2015-01-28 Herbert Gross Winter term 2014 www.iap.uni-jena.de 2 Preliminary Schedule No Date Subject Detailed content 1 12.11. Repetition Correction, handling, multi-configuration 2 19.11. Illumination I Simple illumination problems 3 26.11. Illumination II Non-sequential raytrace 4 03.12. Physical modeling I Gaussian beams, physical propagation 5 10.12. Physical modeling II Polarization 6 07.01. Physical modeling III Coatings 7 14.01. Physical modeling IV Scattering 8 21.01. Tolerancing I Sensitivity, practical procedure 9 28.01. Tolerancing II Adjustment, thermal loading, ghosts Adaptive optics, stock lens matching, index fit, Macro language, 10 04.02. Additional topics coupling Zemax-Matlab 3 Content 1. Adjustment 2. Ghosts 3. Thermal loading Compensators . Compensators: - changeable system parameter to partly compensate the influence of tolerances - compensators are costly due to an adjustment step in the production - usually the tolerances can be enlarged, which lowers the cost of components - clever balance of cost and performance between tolerances and adjustment . Adjustment steps should be modelled to lear about their benefit, observation of criterias, moving width,... Special case: image position compensates for tolerances of radii, indices, thickness . Centeriung lenses: lateral shift of one lens to get a circular symmetric point spread function on axis . Adjustment of air distances between lenses to adjust for spherical aberration, afocal image position,... centering lens Adjustment of Objective Lenses t . Adjustment of air gaps to t2 t4 t6 8 optimize spherical aberration . Reduced optimization setup c c c c j , j 2,4,6,8 j jo j k1,4 tk . Compensates residual aberrations due to tolerances (radii, thicknesses, refractive indices) d2 d4 d6 d8 c20 c40 c60 c80 Wrms nominal 0.77300 0.17000 3.2200 2.0500 0.00527 -0.0718 0.00232 0.01290 0.0324 d2 varied 0.77320 0.17000 3.2200 2.0500 0.04144 -0.07586 0.00277 0.12854 d4 varied 0.77300 0.17050 3.2200 2.0500 0.03003 -0.07461 0.00264 0.01286 d6 varied 0.77300 0.17000 3.2250 2.0500 0.00728 -0.07367 0.00275 0.01284 d8 varied 0.77300 0.17000 3.2200 2.0550 0.005551 -0.0717 0.00235 0.01290 optimized 0.77297 0.16942 3.12670 3.2110 0.000414 0.00046 0.00030 0.01390 0.00468 Adjustment of Objective Lenses . Significant improvement for one wavelength on axis . Possible decreased performance in the field Wrms in 0.3 480 nm solid lines : nominal 546 nm dashed lines : adjusted 644 nm 0.15 improve- ment y/y 0 max 0 0.5 1 7 Adjustment and Compensation . Example Microscopic lens . Adjusting: 1. Axial shifting lens : focus 2. Clocking: astigmatism 3. Lateral shifting lens: coma . Ideal : Strehl DS = 99.62 % With tolerances : DS = 0.1 % After adjusting : DS = 99.3 % Ref.: M. Peschka 8 Adjustment and Compensation . Sucessive steps of improvements Ref.: M. Peschka 9 Glare and Polarization . Filtering of polarized glare light Straylight and Ghost Images What is Stray light? . Diffraction at aperture diffraction-limited PSF, blurred image . Ghosts specular reflections from imperfectly coated refractive surfaces . Unwanted diffraction orders imperfect diffracting surfaces generate spurious images (e.g. Unintentional gratings from diamond turning process) Ref: K. Uhlendorf 11 What is Stray light? . Scatter from structures . Scatter from optical surfaces contamination and sub-wavelength surface defects . Thermal emission from optical and mechanical surfaces Ref: K. Uhlendorf 12 Ghost Images Ghost image in photographic lenses: Reflex film / surface Ref: K. Uhlendorf, D. Gängler Straylight and Ghost Images 3 4 . Calculation of reflected light 5 6 sequence 6 - 4 sequence 5 - 3 . Colour effects due to coatings 15 - 11 14 - 11 sequence 13 - 4 sequence 13 - 5 sequence 20 - 18 20 - 18 6 - 4 5 - 3 9 - 3 sequence 7 - 2 sequence 6 - 4 7 - 2 Heating of Optical Systems . Rise of temperature: 1. Scaling of components in size 2. Stress and strain (birefringence), especially at the glass-metal interface 3. Change of refractive indices with temperature (mostly dominant effect) . Reasons for changes in temperature: - environmental changes - absorption of light in components Problem: depends on actual power level . Homogeneous increase in temperature: usually not critical, can be compensated by focussing . Temperature gradients inside the lenses: - very critical, if transverse oriented - chnages of wavefront accross the pupil . Boundary conditions in optical systems: - heat conduction via mountings (dominant) - air convection - T4 radiation Thermo-mechanical Modellierung . Physical modelling: 2T 1T 2T Q - heat conduction equation 2 2 0 - thermal loading by radiation absorption r r r z K - stress-strain by elasticity equations dP(r, z) . Iterative calculation: Q(r, z) I(r, z) thermal effects influences beam profiles dV . Practice: boundary conditions only poorly known absorption of effects on optical radiation system: 1. n-profil thermal analysis 2. Deformations mechanical geometrical analysis analysis 3. Birefringence thermal boundary conditions mechanical boundary conditions Heating of Lens Systems . Homogeneous rise of temperature: typical not very critical, compensated by defocussing . Heating by absorption and internal heating by the signal light 2T 1T 2T Q - Heat equation 0 r 2 r r z 2 K dP(r, z) - source term Q(r, z) I(r, z) dV - gradients are the problem: lensing effects . Boundary conditions badly defined: - heat flow and cooling by mechanical parts - cooling by air turbulence . Totally three different effects: 1. geometric expansion 2. index gradients due to dn/dT 3. material stress and birefringence Heated Lens . Example: heated lens . Calculated by finite elements Temperature Deformation axial Deformation radial T(r,z) u(r,z) v(r,z) r r r 10 10 10 5 5 5 0 z 0 z 0 z 0 1 2 3 4 5 6 0 1 2 3 4 5 6 0 1 2 3 4 5 6 Temperature Effects . FE calculation of temperature degradation of a microscopic lens . Especially hot spot in the object space due to oil-parameters and high energy density . Example: 1. Distribution of temperature 2. Cold and hot Psf Ref: S. Förster Thermal Loading case c) : . Thermal loading inside the radial parabolic objective lens due to absorption gradient case a) : T of . Parabolic profile of temperature immersion and refractive index . Special effects in the immersion liquid: Strehl ratio drops down . Compensation by refocusing is possible D DS S 1 1 refocused 0.8 without refocusing 0.95 0.6 0.4 0.9 0.2 T 0 T [grd] 0.85 0 5 10 15 20 -5 0 5 [grd] Material Data Expansion Young modul E Type Material in 10-6 m/grd in 103 N /mm2 Glass BK7 7.1 81 KzFSN4 4.5 60 LF5 9.1 59 LaK9 6.3 110 PK51A 12.7 73 Plastics Polycarbonat 69 CR 39 100 Crystals Quartz 0.55 72 Zerodur 0.05 91 Diamond 0.8 1050 ZnSe 7.1 70 Metals Aluminium 24 6800 Invar 1.0 141 Steel 14.7 193 Athermalization . Change of focal length 1 dn Coefficient f f T Material n 1dT in 10-6 m/grd . Opto-thermal coefficient TiF6 20.94 1 dn BK1 3.28 n 1 dT LaKN9 0.32 BAK4 -0.23 KzFS1 -2.89 . System with focal powers Fj : ZnSe -28.24 Fj j silica -64.1 j Fges . Homogeneous heating of complete Germanium -85.19 system: - only defocussing - mechanical expansion compensates change of focal length - special optimization of materials, mechanical design and materials necessary .
Load more

Recommended publications
  • Optically-Athermalized Construction Optical Design for the IMACS Short Camera
    Optically-athermalized construction optical design for the IMACS Short camera Harland W. Epps1, and Brian M. Sutin2 1 University of California Observatories/Lick Observatory Santa Cruz, California 95064 2 Observatories of the Carnegie Institution of Washington Pasadena, California 91101 ABSTRACT The optical performance of a large, optically fast, all-refracting spectrograph camera is extremely sensitive to potential temperature changes which might occur during an extended single observation, over the duration of an observing run, and/or on seasonal time scales. A small temperature change, even at the level of a few degrees C, will lead to changes in the refractive indices of the glasses and the coupling medium, changes in the lens-element geometries and in the dimensions of the lens cell. These effects combine in a design-speci®c manner to cause potential changes of focus and magni®cation within the camera as well as inherent loss of image quality. We have used an optical design technique originally developed for the Smithsonian Astrophysical Observatory's BINOSPEC1,2 instrument in order to produce a construction optical design for the Carnegie IMACS Short camera. This design combines the above-mentioned temperature-dependent parameter variations in such a way that their net effect upon focus and magni®cation is passively reduced to negligible residuals, without the use of high-expansion plastics, "negative-c.t.e." mechanisms or active control within the lens cell. Simultaneously, the design is optimized for best inherent image quality at any temperature within the designated operating range. The optically-athermalized IMACS Short camera is under construction. We present its quantitative optical design together with our assessment of its expected performance over a (T= -4.0 to +20.0) C temperature range.
    [Show full text]
  • 12 Considerations for Thermal Infrared Camera Lens Selection Overview
    12 CONSIDERATIONS FOR THERMAL INFRARED CAMERA LENS SELECTION OVERVIEW When developing a solution that requires a thermal imager, or infrared (IR) camera, engineers, procurement agents, and program managers must consider many factors. Application, waveband, minimum resolution, pixel size, protective housing, and ability to scale production are just a few. One element that will impact many of these decisions is the IR camera lens. USE THIS GUIDE AS A REFRESHER ON HOW TO GO ABOUT SELECTING THE OPTIMAL LENS FOR YOUR THERMAL IMAGING SOLUTION. 1 Waveband determines lens materials. 8 The transmission value of an IR camera lens is the level of energy that passes through the lens over the designed waveband. 2 The image size must have a diameter equal to, or larger than, the diagonal of the array. 9 Passive athermalization is most desirable for small systems where size and weight are a factor while active 3 The lens should be mounted to account for the back athermalization makes more sense for larger systems working distance and to create an image at the focal where a motor will weigh and cost less than adding the plane array location. optical elements for passive athermalization. 4 As the Effective Focal Length or EFL increases, the field 10 Proper mounting is critical to ensure that the lens is of view (FOV) narrows. in position for optimal performance. 5 The lower the f-number of a lens, the larger the optics 11 There are three primary phases of production— will be, which means more energy is transferred to engineering, manufacturing, and testing—that can the array.
    [Show full text]
  • Athermal Design and Analysis for WDM Applications
    Header for SPIE use Athermal design and analysis for WDM applications Keith B. Doyle Optical Research Associates Westborough, MA Jeffrey M. Hoffman Optical Research Associates Tucson, AZ ABSTRACT Telecommunication wavelength division multiplexing systems (WDM) demand high fiber-to-fiber coupling to minimize signal loss and maximize performance. WDM systems, with increasing data rates and narrow channel spacing, must maintain performance over the designated wavelength band and across a wide temperature range. Traditional athermal optical design techniques are coupled with detailed thermo-elastic analyses to develop an athermal optical system under thermal soak conditions for a WDM demultiplexer. The demultiplexer uses a pair of doublets and a reflective Littrow- mounted grating employed in a double-pass configuration to separate nine channels of data from one input fiber into nine output fibers operating over the C-band (1530 to 1561.6 nm). The optical system is achromatized and athermalized over a 0°Cto70°C temperature range. Detailed thermo-elastic analyses are performed via a MSC/NASTRAN finite element model. Finite element derived rigid-body positional errors and optical surface deformations are included in the athermalization process. The effects of thermal gradients on system performance are also evaluated. A sensitivity analysis based on fiber coupling efficiency is performed for radial, axial, and lateral temperature gradients. Keywords: wavelength division multiplexing, athermal optical design, fiber coupling efficiency, thermo-elastic analysis, integrated modeling, thermal gradients 1. INTRODUCTION In the field of telecommunications, wavelength-division multiplexing is used in fiber-optic systems to transmit signals at different wavelengths through a single fiber to increase transmission capacity without having to install new fiber.
    [Show full text]
  • Comparison of the Thermal Effects on LWIR Optical Designs Utilizing Different Infrared Optical Materials
    Invited Paper Comparison of the thermal effects on LWIR optical designs utilizing different infrared optical materials Jeremy Huddleston, Alan Symmons, Ray Pini LightPath Technologies, Inc., 2603 Challenger Tech Ct, Ste 100, Orlando, FL, USA 32826 ABSTRACT The growing demand for lower cost infrared sensors and cameras has focused attention on the need for low cost optics for the long wave and mid-wave infrared region. The thermal properties of chalcogenides provide benefits for optical and optomechanical designers for the athermalization of lens assemblies as compared to Germanium, Zinc Selenide and other more common infrared materials. This investigation reviews typical infrared materials’ thermal performance and the effects of temperature on the optical performance of lens systems manufactured from various optical materials. Keywords: Precision glass molding, long wave infrared, LWIR, thermal camera, athermal, athermalization, chalcogenide, SWaP-C. 1. INTRODUCTION Over the past ten years, the prices for thermal imaging sensors have decreased dramatically. The resulting cost savings has significantly increased the quantities of thermal imagers sold. However, the high cost of traditional materials for thermal lenses has become the limiting factor in overall camera costs. Optics manufacturers are looking for high volume, low cost methods to produce infrared optical systems. The technological roadmap for infrared optical systems is following the same path that visible camera systems have followed in the recent past; from large SLR type
    [Show full text]
  • Thermal Technology Glossary June 2018 Table of Contents 1
    Glossary Thermal technology glossary June 2018 Table of contents 1. AGC 3 2. Detection range 3 2.1 Johnson’s criteria 4 3. Electromagnetic spectrum 4 4. Emissivity 5 5. Exposure zone 5 6. Lenses 6 6.1 Athermalized lenses 6 7. NETD 6 8. NUC 7 9. Pixel pitch 7 10. Sensors 7 10.1 Cooled sensors 7 10.2 Uncooled sensors 7 10.2.1 Microbolometers 7 11. Sun safe 8 12. Thermography 8 2 1. AGC Automatic gain control (AGC) is a controlling algorithm for automatically adjusting the gain and offset, to deliver a visually pleasing and stable image that is suitable for video analytics. By deploying different AGC techniques, both rapid and slow scene changes can be controlled to optimize the resulting image regarding brightness, contrast, and other image-quality properties. A rapid scene change, that is, a rapid change in the incoming signal levels, could, for a thermal camera, be when something cold or hot enters the scene, for instance a hot truck engine. The corresponding scene change for a visual camera could be when the sun disappears behind a cloud. Snow Heat from a running truck AGC also controls whether the output mapping from the sensor’s 14-bit signal level to the 8-bit image is done linearly or by using a histogram-equalization curve. Histogram equalization redistributes the incoming signal levels, resulting in better image contrast. For example, in a scene with a big flat back- ground and one small but very warm object, a linear curve would waste signal levels that are between the object and the background.
    [Show full text]
  • Graphically Selecting Optical Material for Color Correction and Passive Athermalization
    Raghad Ismail Ibrahim.Int. Journal of Engineering Research and Applications ww.ijera.com ISSN: 2248-9622, Vol. 6, Issue 4, (Part - 5) April 2016, pp.38-41 RESEARCH ARTICLE OPEN ACCESS Graphically Selecting Optical Material for Color Correction and Passive Athermalization Raghad Ismail Ibrahim * *(Physics Department, Al-Mustansiryah University, and CollegeOf Education) ABSTRACT This paper presents pair optical glass by using a graphical method for selecting achromatize and athermalize an imaging lens. An athermal glass map that plots thermal glass constant versus inverse Abbe number is derived through analysis of optical glasses in visible light. By introducing the equivalent Abbe number and equivalent thermal glass constant, although it is a multi-lens system, we have a simple way to visually identify possible optical materials. ZEMAX will be used to determine the change in focus through the expected temperature changes in Earth orbit. The thermal defocuses over -20°C to +60°C are reduced to be much less than the depth of focus of the system. Keywords-Athermal glass, ZEMAX, graphical method for selecting, athermalize lens. I. INTRODUCTION Order to solve these difficulties, in this Athermalization is the principle of paper we introduce the equivalent Abbe number and stabilizing the optical performance with respect to equivalent thermal glass constant. Even though a temperature. Any temperature changes experienced lens system is composed of many elements, we can by the optics may be with respect to time or space or simply identify a pair of materials that satisfies the both. Time refers to a uniform heat soak across all athermal and achromatic conditions, by selecting the the optics, and space refers to a gradient across the corresponding materials for an equivalent lens from optics resulting in each lens (and housing) being a an athermal glass map and test them by application different temperature, or there being a radial change of Zemax software for a good solution.
    [Show full text]
  • Passive Athermalization of an Infrared Optical System OPTI 521 Tutorial Report James Champagne
    1 Passive Athermalization of an Infrared Optical System OPTI 521 Tutorial Report James Champagne Introduction This tutorial will cover the design of an athermal lens mount for an infrared double-Gauss objective. This objective will need to be able to survive a space environment. It will experience large temperature changes and needs to remain in focus so imaging can occur continuously. The lens will image the earth through wavelengths of 3-5 microns. Normal optical glass does not transmit in this range so infrared glasses were used in the optical design. Infrared glasses tend to have high changes in refractive index under temperature changes and thus tend to cause defocus in infrared optical systems. ZEMAX will be used to determine the change in focus through the expected temperature changes in Earth orbit. A lens mount composed of materials of differing coefficients of thermal expansion will then be designed to compensate the change in focus at the detector plane. Optical Design The optical design of this system was performed in ZEMAX. It is a double-Gauss type objective designed to image over wavelengths 3-5 microns. The lens has a total of 6 lens elements with 5 different glass types. The design also consists of two doublets that will be cemented together. The design covers a full field of view of 20 degrees and will cover a sensor with a 1 inch diagonal (0.707” x 0.707”). With an F/# of 3, the entrance pupil diameter is 1 inch and the effective focal length is 3 inches. This design can easily fit within a cube satellite that has dimensions 10 cm x 10 cm x 10 cm (4” x 4” x 4”).
    [Show full text]
  • Athermalization Bellows Assemblies
    Athermalization Bellows Assemblies FREQUENTLY ASKED QUESTIONS Q: What are athermalization bellows enough that engineers can use it in a well in precision electromechanical assemblies? variety of ways from adjusting optical applications that are sensitive to A: Athermalization (atherm) bellows focus to triggering electro-mechanical temperature. They can be used assemblies are filled and sealed flexible systems at specified temperatures. like thermostats to trigger heat bellows assemblies that translate changes or cooling system valves or other in temperature into precise linear Q: Where is athermalization helpful? components when temperature mechanical motion. A: Atherms are useful in a variety of rises or falls. In precise metering Atherm bellows assemblies take applications. They are commonly used applications, they can adjust advantage of the flexible, expandable in optical applications because of the orifice openings so that the mass flow of nature of precision electroformed metal precision required to maintain the gas or liquid is normalized independent bellows, and the steady volumetric properties of sensitive optics over the of temperature. expansion of incompressible fluids with range of operating temperatures. These assemblies provide changes in temperature. These bellows Other applications put temperature- temperature-dependent mechanical assemblies have known temperature- dependent length change to mechanical actuation without the need for dependent rates of length change use, similar to the operation of a programming or electricity. Their simple, depending upon the fluid used in the thermostat’s bimetallic strip. And robust design lets them operate through assembly. atherm assemblies can shield delicate hundreds of millions of repeatable cycles Each end of the bellows connects to systems from the effects of without drawing power or requiring system components using stock fittings temperature change.
    [Show full text]
  • Optomechanical Design of Nine Cameras for the Earth Observing
    Optomechanical Designof Nine Cameras for the Earth Observing Systems Multi-Angle Imaging Spectral Radiometer, TERRAPlatform Virginia G. Ford, Mary L. White, Eric Hochberg, and Jim McGown Jet Propulsion Laboratory California Institute of Technology ABSTRACT The Multi-Angle Imaging Spectral Radiometer (MISR) is a push-broom instrument using nine cameras to collect data at nine different angles through the atmosphere. The science goals are to monitor global atmospheric particulates, cloud movements, and vegetative changes. The camera optomechanical requirements were: to operate within specification over a temperature range of OC to 1OC; to survive a temperaturerange of -40C to 80C; to survive launch loads and on-orbit radiation; to be non- contaminating both to itself and to other instruments; and to remained aligned though the mission. Each camera has its own lens, detector, and thermal control. The lenses are refractive; thus passive thermal focus compensation and maintaining lens positioning and centering were dominant issues. Because of the number of cameras, modularity was stressed in the design. This paper will describe the final design of the cameras, the driving design considerations, and the results of qualification testing. Keywords: Optomechanicai, refractive lens, passive thermal compensation, lens positioning, MISR, lens centering Figure 1. EOS-TERRA spacecraft with the Multi-.Ugle Imaging Spectral Radiometerinstrument. The nine camera fields- of-view with four spectral wavebands are shown. 1. INTRODUCTION MISR is mounted on thc EOS-TERRA spacecraft, which will orbit around the Earth for up to a six-year mission. The spacecraft will be launched on an ATLAS IIAS rocket from Vanderberg AirforceBase - the launch is currently scheduled on August 27, 1999.
    [Show full text]
  • Design of an Optical System for a 5Th Generation, High
    Proceedings of COBEM 2009 20th International Congress of Mechanical Engineering Copyright © 2009 by ABCM November 15-20, 2009, Gramado, RS DESIGN OF AN OPTICAL SYSTEM FOR A 5TH GENERATION, HIGH PERFORMANCE, AIR-TO-AIR MISSILE, CONSIDERING THE IMAGING PERFORMANCE DEGRADATION DUE TO THE AERODYNAMIC HEATING Leite Junior, Paulo Roberto Comando Geral de Tecnologia Aeroespacial (CTA)/ Instituto de Aeronáutica e Espaço (IAE)/ Divisão de Sistemas de Defesa(ASD) DENEL Aerospace System / South Africa [email protected] Paoli, Eduardo Tadeu Mectron S.A./ DENEL Aerospace System/ South Africa [email protected] Hassmann, Carlos Henrique Gustavo Mectron S.A./ DENEL Aerospace System/ South Africa [email protected] An air-to-air missile is always submitted to extreme condition of temperature, such as a hot runway over a rain forest or desert area and dropping down to very cold conditions at high altitudes. It is evident that the optical system must be able to provide satisfactory image quality under any circumstances without causing any major degradation for the image. The influence of the aerodynamic heating for this missile flying at supersonic speed must be evaluated in respect to optical performance as well. The aerodynamic heating is defined as the rise in temperature of the air adjacent to the external surface of a missile due to compression and friction during the missile flight attached to the aircraft or launched. While it appears relatively easy to calculate the aerodynamic heating, the actual wall temperature attained is the most difficult problem, and most likely a transient one. Further factors need to be included when attempting to estimate the surface temperature of a supersonic missile, such as radiation and conduction.
    [Show full text]
  • Athermalization Techniques in Infrared Systems
    ATHERMALIZATION TECHNIQUES IN INFRARED SYSTEMS JEFFREY T DAIKER OPTI 521 DECEMBER 6, 2010 ABSTRACT A major area of concern when designing infrared systems is the defocus with temperature change due to the nature of lens materials. This tutorial describes how this defocus affects the system performance and discusses some techniques for solving this problem. The key advantages and disadvantages of each technique are identified. INTRODUCTION There is continued interest in developing high performance infrared (IR) systems which are capable of operating in harsh environments with extreme temperatures. The technique for maintaining focus of an IR system over an extended temperature range is called athermalization. The problem is quite challenging as most commonly used IR materials exhibit very large changes in refractive index with temperature, which inherently leads to changes in focal length of the system. Several techniques exist to control this effect and maintain acceptable focus over wide temperature ranges. EFFECT OF TEMPERATURE ON FOCUS Considering the simple case of a single element thin lens, the change in focal length of the lens with temperature is given by / ∆ ∆ ∆ 1 Where: = thermo‐optical coefficient of the lens dn/dT = refractive index change with temperature n = refractive index of the lens = thermal expansion coefficient (TCE) of the lens OPTI 521 – Fall 2010 Tutorial Daiker f = focal length of the lens ∆ = temperature change Further considering the simple case of this lens housing, the expansion of the housing with
    [Show full text]
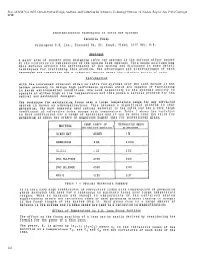
  • Athermalization Techniques in Infrared Systems
    Proc.ofSPIEVol.0655,OpticalSystemDesign,Analysis,andProductionforAdvancedTechnologySystems,ed.Fischer,Rogers(Apr1986)Copyright SPIE Athermalisation Techniques in Infra Red Systems Veronica Povey Pilkington P.E. Ltd., Glascoed Rd, St. Asaph, Clwyd, LL17 OLL, U.K. Abstract A major area of concern when designing infra red systems is the defocus effect caused by the variation in temperature of the system from ambient. This paper outlines how this defocus affects the performance of the system and discusses in some detail techniques for overcoming this problem. The advantages and disadvantages of each technique are identified and a trade-off matrix shows the relative merits of each. Introduction With the increased interest shown in infra red systems over the last decade it has become necessary to design high performance systems which are capable of functioning in harsh environmental conditions. One such capability is the systems ability to operate at either high or low temperatures and this poses a serious problem for the optical and mechanical designer. The technique for maintaining focus over a large temperature range for any infra-red system is known as athermalisation. This becomes a significant problem in that germanium, the most commonly used optical material in the infra red has a very large coefficient of refractive index change with temperature. Table 1 shows the variation in this coefficient for a range of materials and it can be seen that the value for germanium is about two orders of magnitude higher than for conventional glass. TEMP COEFF OF REFRACTIVE INDEX MATERIAL REFRACTIVE INDEX xIO-~ IO MICRONS GLASS BK7 +0025 I 51 GERMANIUM +396 4003 SILICON +I 62 238 ZINC SULPHIDE +050 220 ZINC SELENIDE +060 240 KRS-5 -235 237 Table 1 - Optical Materials Summary It is this very high coefficient of refractive index with temperature of germanium which dictates the need for a technique to maintain focus over large temperature ranges.
    [Show full text]