DOCSLIB.ORG

Graphically Selecting Optical Material for Color Correction and Passive Athermalization

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Graphically Selecting Optical Material for Color Correction and Passive Athermalization Raghad Ismail Ibrahim.Int. Journal of Engineering Research and Applications ww.ijera.com ISSN: 2248-9622, Vol. 6, Issue 4, (Part - 5) April 2016, pp.38-41 RESEARCH ARTICLE OPEN ACCESS Graphically Selecting Optical Material for Color Correction and Passive Athermalization Raghad Ismail Ibrahim * *(Physics Department, Al-Mustansiryah University, and CollegeOf Education) ABSTRACT This paper presents pair optical glass by using a graphical method for selecting achromatize and athermalize an imaging lens. An athermal glass map that plots thermal glass constant versus inverse Abbe number is derived through analysis of optical glasses in visible light. By introducing the equivalent Abbe number and equivalent thermal glass constant, although it is a multi-lens system, we have a simple way to visually identify possible optical materials. ZEMAX will be used to determine the change in focus through the expected temperature changes in Earth orbit. The thermal defocuses over -20°C to +60°C are reduced to be much less than the depth of focus of the system. Keywords-Athermal glass, ZEMAX, graphical method for selecting, athermalize lens. I. INTRODUCTION Order to solve these difficulties, in this Athermalization is the principle of paper we introduce the equivalent Abbe number and stabilizing the optical performance with respect to equivalent thermal glass constant. Even though a temperature. Any temperature changes experienced lens system is composed of many elements, we can by the optics may be with respect to time or space or simply identify a pair of materials that satisfies the both. Time refers to a uniform heat soak across all athermal and achromatic conditions, by selecting the the optics, and space refers to a gradient across the corresponding materials for an equivalent lens from optics resulting in each lens (and housing) being a an athermal glass map and test them by application different temperature, or there being a radial change of Zemax software for a good solution. in temperature across an optic. Athermal systems are highly desirable for a multitude of applications in the II.THERMAL DEFOCUS broad field of integrated optics such as mobile phone The variations of temperature change the and black box cameras, so, it is important to develop radius of curvature, lens thickness and air spacing, an athermal optical system: an optical system that is and refractive index. These changes cause alignment insensitive to an environment’s thermal change and errors and degrade the optical performance.An the resulting system defocus. To reduce thermal and athermal system is meant to have stable optical chromatic errors, many design methods have been performance, even during temperature changes in reported. Perry studied the effect of temperature the optical system [6]. changes on optical performance in infrared optics. Table 1 lists the quantitative variations of Rogers showed that the multi-lens system could be design parameters due to temperature change [7], the achromatized and athermalized with three materials parameters of n (T), R (T), t (T), and L (T) are by solving three equations, but it was difficult to find measured values after temperature change. The a proper combination of materials [1].As alternative coefficients of a linear thermal expansion (CTE) are approaches to overcome these problems, graphic designated as αg for the lens material and αm for the methods have been developed. Rayces and Lebich housing material, respectively. proposed a γV-V diagram and showed that chromatic aberration corresponds to the area of a Table 1. Variations of design parameters due to triangle [2]. Tamagawa, et al. suggested other Temperature change [8]. graphical approaches by plotting the thermal dispersive power versus chromatic dispersive power and included a discussion of selecting the element powers in addition to the element materials [3, 4]. Schwertz studied how developing an optical system that is insensitive to an environment’s thermal change and the resulting system defocus [5], this research has been performed mainly on infrared optics, and there are few studies on visible optics. In www.ijera.com 38|P a g e Raghad Ismail Ibrahim.Int. Journal of Engineering Research and Applications ww.ijera.com ISSN: 2248-9622, Vol. 6, Issue 4, (Part - 5) April 2016, pp.38-41 The parameter dn/dT denotes the variation 휙 1 = 푇1 (7) of the refractive index with temperature. 휙 푇1 − 푇2 The expansion and contraction of a material due to 휙2 푇2 temperature changes is governed by a material’s = − (8) 휙 푇1 − 푇2 coefficient of thermal expansion, α, which has units If we design a doublet where the of 10-6m/°C (or ppm/°C). The change in length (L) achromatic doublet and athermal doublet equations of a material due to a temperature change is given by are all satisfied (Equations 5-8), the result is an Equation 1. achrothermic system: a system that is both 훥퐿 = 훼퐿훥푇 (1) achromatic and athermal as shown in Equation 9: Thermal defocus is the change in the focus 1 2 position on axis with temperature changes due to the = (9) 푇1 푇2 variation of the index of refraction with temperature IV. GRAPHICAL METHOD FOR (dn/dT) and the expansion of the material. The CHOOSING ACHROTHERM analogous equation quantifying the change in focal GLASS : length of a lens in air with temperature is given by By plotting the therm-optic coefficient (γ) Equation2: vs. the inverse color ν-number [9], we can visually 훥푓 = 훾푓훥푇 (2) identify two materials that can be used to develop an Where γ is the therm-optic coefficient. achrothermic system, this method not only helps γ can be defined using Equation 3: 1 푑푛 identify two available optical materials, but also 훾 = − 훼 (3) helps identify the CTE of the housing material 푛 − 1 푑푇 required for a housed achrothermic solution. As Whereα is Coefficient of linear thermal expansion 1 푑푟 1 푑푟 shown in Figure 1, the y-intercept provides the 훼 = 1 = 2 required housing material via a line that extends 푟1 푑푇 푟2 푑푇 through two materials and crosses the y-axis. In the case that a single housing material with the required III. ACHROMATIC & ATHERMAL CTE is unavailable, the required CTE can be DOUBLET EQUATIONS achieved using a bimetallic housing or alternative A common optical element is the mechanical mounting solution. achromatic doublet, which uses a positive and Figure 1 shows the athermal glass map for negative element of different materials with equal Schott glass [10]. Involves plotting the thermal glass and opposite amounts of chromatic aberration to constant versus the inverse Abbe number, we can correct for color. Assuming an element is in air, the visually identify two materials that satisfy the ν-number (inverse dispersion) for an arbitrary athermal and achromatic conditions [11] . waveband defined by the longest, shortest, and middle wavelength is given by Equation 4: 푛 − 1 = 푚푖푑 (4) 푛푠푕표푟푡 − 푛푙표푛푔 If Equations 5 and 6 are satisfied, the result is an achromatic doublet, each element is required to have power: 휙 푣 1 = 1 (5) 휙 1 − 2 휙 2 = − 2 (6) 휙 1 − 2 The optimal solution is one that has two elements with the largest ν-number difference: Δν. Fig. 1. Athermal glass map plotting γ v.s. 1/for A larger Δν results in longer focal lengths visible Schott glasses. (lower power) and shallower radii (reduces aberrations and increases optical performance). By In Fig. 1, any two materials (M1, M2) that looking at the glass map, it is simple to visually can be connected by a line that passes through the select a crown and flint glass that have a large ν- origin will provide athermal and achromatic number difference. Analogously, we can use the solutions. In other words, if one material is known inverse of the therm-optic coefficient (equation), on an athermal glass map, like M1(1/v1, γ1), then usually called the thermal ν number, in our another material(M2) that serves color correction achromatic equations to design an athermal double and passive athermalization can be found on a line as follows in Equations 7 and 8: connecting two materials. Even if a lens system is composed of many elements, the equivalent Abbe www.ijera.com 39|P a g e Raghad Ismail Ibrahim.Int. Journal of Engineering Research and Applications ww.ijera.com ISSN: 2248-9622, Vol. 6, Issue 4, (Part - 5) April 2016, pp.38-41 number and equivalent thermal glass constant reduce Thickness should be changed in the design the problem to be that of a two-element system as a above when a pair of glasses tested every time until doublet. Unlike some of the previous methods using the image shows clear. The lens layout for double complex triangle geometry [3, 4]. design in Fig.3. V. RESULT AND DISCUSSION We will use the method as shown in Fig.1 to visually determine exactly what material is required to achromatize and athermalize the multi- lens system. We know we want the slope of two different materials to be equal in order to achieve color correction and athermalization; any two materials that can be connected by a line that passes Fig.3. Optical Layout for athermal double design. through the origin will provide an achrothermic solution as shown in table 2. The important thing in athermal design is Table 2. Achrothermic Glasses Used in a Double the RMS spot diagram, which shows that with design. refocusing, the optical performance holds up well Number of Glass 1 Glass 2 over the field of view for extreme observing double temperature. Blur sizes at ‐100⁰C, 0⁰C, and +100⁰C achromatic lens (from left to right) shown in Fig .4. 1 N-FK5 F2 2 N-PSK53 SF66 3 BK10 N-BASF2 4 N-KZFS11 N-SF66 Table 2 would provide athermal glasses solution in air for visible.
Load more

Recommended publications
  • Optically-Athermalized Construction Optical Design for the IMACS Short Camera
    Optically-athermalized construction optical design for the IMACS Short camera Harland W. Epps1, and Brian M. Sutin2 1 University of California Observatories/Lick Observatory Santa Cruz, California 95064 2 Observatories of the Carnegie Institution of Washington Pasadena, California 91101 ABSTRACT The optical performance of a large, optically fast, all-refracting spectrograph camera is extremely sensitive to potential temperature changes which might occur during an extended single observation, over the duration of an observing run, and/or on seasonal time scales. A small temperature change, even at the level of a few degrees C, will lead to changes in the refractive indices of the glasses and the coupling medium, changes in the lens-element geometries and in the dimensions of the lens cell. These effects combine in a design-speci®c manner to cause potential changes of focus and magni®cation within the camera as well as inherent loss of image quality. We have used an optical design technique originally developed for the Smithsonian Astrophysical Observatory's BINOSPEC1,2 instrument in order to produce a construction optical design for the Carnegie IMACS Short camera. This design combines the above-mentioned temperature-dependent parameter variations in such a way that their net effect upon focus and magni®cation is passively reduced to negligible residuals, without the use of high-expansion plastics, "negative-c.t.e." mechanisms or active control within the lens cell. Simultaneously, the design is optimized for best inherent image quality at any temperature within the designated operating range. The optically-athermalized IMACS Short camera is under construction. We present its quantitative optical design together with our assessment of its expected performance over a (T= -4.0 to +20.0) C temperature range.
    [Show full text]
  • 12 Considerations for Thermal Infrared Camera Lens Selection Overview
    12 CONSIDERATIONS FOR THERMAL INFRARED CAMERA LENS SELECTION OVERVIEW When developing a solution that requires a thermal imager, or infrared (IR) camera, engineers, procurement agents, and program managers must consider many factors. Application, waveband, minimum resolution, pixel size, protective housing, and ability to scale production are just a few. One element that will impact many of these decisions is the IR camera lens. USE THIS GUIDE AS A REFRESHER ON HOW TO GO ABOUT SELECTING THE OPTIMAL LENS FOR YOUR THERMAL IMAGING SOLUTION. 1 Waveband determines lens materials. 8 The transmission value of an IR camera lens is the level of energy that passes through the lens over the designed waveband. 2 The image size must have a diameter equal to, or larger than, the diagonal of the array. 9 Passive athermalization is most desirable for small systems where size and weight are a factor while active 3 The lens should be mounted to account for the back athermalization makes more sense for larger systems working distance and to create an image at the focal where a motor will weigh and cost less than adding the plane array location. optical elements for passive athermalization. 4 As the Effective Focal Length or EFL increases, the field 10 Proper mounting is critical to ensure that the lens is of view (FOV) narrows. in position for optimal performance. 5 The lower the f-number of a lens, the larger the optics 11 There are three primary phases of production— will be, which means more energy is transferred to engineering, manufacturing, and testing—that can the array.
    [Show full text]
  • Athermal Design and Analysis for WDM Applications
    Header for SPIE use Athermal design and analysis for WDM applications Keith B. Doyle Optical Research Associates Westborough, MA Jeffrey M. Hoffman Optical Research Associates Tucson, AZ ABSTRACT Telecommunication wavelength division multiplexing systems (WDM) demand high fiber-to-fiber coupling to minimize signal loss and maximize performance. WDM systems, with increasing data rates and narrow channel spacing, must maintain performance over the designated wavelength band and across a wide temperature range. Traditional athermal optical design techniques are coupled with detailed thermo-elastic analyses to develop an athermal optical system under thermal soak conditions for a WDM demultiplexer. The demultiplexer uses a pair of doublets and a reflective Littrow- mounted grating employed in a double-pass configuration to separate nine channels of data from one input fiber into nine output fibers operating over the C-band (1530 to 1561.6 nm). The optical system is achromatized and athermalized over a 0°Cto70°C temperature range. Detailed thermo-elastic analyses are performed via a MSC/NASTRAN finite element model. Finite element derived rigid-body positional errors and optical surface deformations are included in the athermalization process. The effects of thermal gradients on system performance are also evaluated. A sensitivity analysis based on fiber coupling efficiency is performed for radial, axial, and lateral temperature gradients. Keywords: wavelength division multiplexing, athermal optical design, fiber coupling efficiency, thermo-elastic analysis, integrated modeling, thermal gradients 1. INTRODUCTION In the field of telecommunications, wavelength-division multiplexing is used in fiber-optic systems to transmit signals at different wavelengths through a single fiber to increase transmission capacity without having to install new fiber.
    [Show full text]
  • Comparison of the Thermal Effects on LWIR Optical Designs Utilizing Different Infrared Optical Materials
    Invited Paper Comparison of the thermal effects on LWIR optical designs utilizing different infrared optical materials Jeremy Huddleston, Alan Symmons, Ray Pini LightPath Technologies, Inc., 2603 Challenger Tech Ct, Ste 100, Orlando, FL, USA 32826 ABSTRACT The growing demand for lower cost infrared sensors and cameras has focused attention on the need for low cost optics for the long wave and mid-wave infrared region. The thermal properties of chalcogenides provide benefits for optical and optomechanical designers for the athermalization of lens assemblies as compared to Germanium, Zinc Selenide and other more common infrared materials. This investigation reviews typical infrared materials’ thermal performance and the effects of temperature on the optical performance of lens systems manufactured from various optical materials. Keywords: Precision glass molding, long wave infrared, LWIR, thermal camera, athermal, athermalization, chalcogenide, SWaP-C. 1. INTRODUCTION Over the past ten years, the prices for thermal imaging sensors have decreased dramatically. The resulting cost savings has significantly increased the quantities of thermal imagers sold. However, the high cost of traditional materials for thermal lenses has become the limiting factor in overall camera costs. Optics manufacturers are looking for high volume, low cost methods to produce infrared optical systems. The technological roadmap for infrared optical systems is following the same path that visible camera systems have followed in the recent past; from large SLR type
    [Show full text]
  • Thermal Technology Glossary June 2018 Table of Contents 1
    Glossary Thermal technology glossary June 2018 Table of contents 1. AGC 3 2. Detection range 3 2.1 Johnson’s criteria 4 3. Electromagnetic spectrum 4 4. Emissivity 5 5. Exposure zone 5 6. Lenses 6 6.1 Athermalized lenses 6 7. NETD 6 8. NUC 7 9. Pixel pitch 7 10. Sensors 7 10.1 Cooled sensors 7 10.2 Uncooled sensors 7 10.2.1 Microbolometers 7 11. Sun safe 8 12. Thermography 8 2 1. AGC Automatic gain control (AGC) is a controlling algorithm for automatically adjusting the gain and offset, to deliver a visually pleasing and stable image that is suitable for video analytics. By deploying different AGC techniques, both rapid and slow scene changes can be controlled to optimize the resulting image regarding brightness, contrast, and other image-quality properties. A rapid scene change, that is, a rapid change in the incoming signal levels, could, for a thermal camera, be when something cold or hot enters the scene, for instance a hot truck engine. The corresponding scene change for a visual camera could be when the sun disappears behind a cloud. Snow Heat from a running truck AGC also controls whether the output mapping from the sensor’s 14-bit signal level to the 8-bit image is done linearly or by using a histogram-equalization curve. Histogram equalization redistributes the incoming signal levels, resulting in better image contrast. For example, in a scene with a big flat back- ground and one small but very warm object, a linear curve would waste signal levels that are between the object and the background.
    [Show full text]
  • Optical Design with Zemax for Phd - Advanced
    Optical Design with Zemax for PhD - Advanced Seminar 8 : Tolerancing II 2015-01-28 Herbert Gross Winter term 2014 www.iap.uni-jena.de 2 Preliminary Schedule No Date Subject Detailed content 1 12.11. Repetition Correction, handling, multi-configuration 2 19.11. Illumination I Simple illumination problems 3 26.11. Illumination II Non-sequential raytrace 4 03.12. Physical modeling I Gaussian beams, physical propagation 5 10.12. Physical modeling II Polarization 6 07.01. Physical modeling III Coatings 7 14.01. Physical modeling IV Scattering 8 21.01. Tolerancing I Sensitivity, practical procedure 9 28.01. Tolerancing II Adjustment, thermal loading, ghosts Adaptive optics, stock lens matching, index fit, Macro language, 10 04.02. Additional topics coupling Zemax-Matlab 3 Content 1. Adjustment 2. Ghosts 3. Thermal loading Compensators . Compensators: - changeable system parameter to partly compensate the influence of tolerances - compensators are costly due to an adjustment step in the production - usually the tolerances can be enlarged, which lowers the cost of components - clever balance of cost and performance between tolerances and adjustment . Adjustment steps should be modelled to lear about their benefit, observation of criterias, moving width,... Special case: image position compensates for tolerances of radii, indices, thickness . Centeriung lenses: lateral shift of one lens to get a circular symmetric point spread function on axis . Adjustment of air distances between lenses to adjust for spherical aberration, afocal image position,... centering lens Adjustment of Objective Lenses t . Adjustment of air gaps to t2 t4 t6 8 optimize spherical aberration . Reduced optimization setup c c c c j , j 2,4,6,8 j jo j k1,4 tk .
    [Show full text]
  • Passive Athermalization of an Infrared Optical System OPTI 521 Tutorial Report James Champagne
    1 Passive Athermalization of an Infrared Optical System OPTI 521 Tutorial Report James Champagne Introduction This tutorial will cover the design of an athermal lens mount for an infrared double-Gauss objective. This objective will need to be able to survive a space environment. It will experience large temperature changes and needs to remain in focus so imaging can occur continuously. The lens will image the earth through wavelengths of 3-5 microns. Normal optical glass does not transmit in this range so infrared glasses were used in the optical design. Infrared glasses tend to have high changes in refractive index under temperature changes and thus tend to cause defocus in infrared optical systems. ZEMAX will be used to determine the change in focus through the expected temperature changes in Earth orbit. A lens mount composed of materials of differing coefficients of thermal expansion will then be designed to compensate the change in focus at the detector plane. Optical Design The optical design of this system was performed in ZEMAX. It is a double-Gauss type objective designed to image over wavelengths 3-5 microns. The lens has a total of 6 lens elements with 5 different glass types. The design also consists of two doublets that will be cemented together. The design covers a full field of view of 20 degrees and will cover a sensor with a 1 inch diagonal (0.707” x 0.707”). With an F/# of 3, the entrance pupil diameter is 1 inch and the effective focal length is 3 inches. This design can easily fit within a cube satellite that has dimensions 10 cm x 10 cm x 10 cm (4” x 4” x 4”).
    [Show full text]
  • Athermalization Bellows Assemblies
    Athermalization Bellows Assemblies FREQUENTLY ASKED QUESTIONS Q: What are athermalization bellows enough that engineers can use it in a well in precision electromechanical assemblies? variety of ways from adjusting optical applications that are sensitive to A: Athermalization (atherm) bellows focus to triggering electro-mechanical temperature. They can be used assemblies are filled and sealed flexible systems at specified temperatures. like thermostats to trigger heat bellows assemblies that translate changes or cooling system valves or other in temperature into precise linear Q: Where is athermalization helpful? components when temperature mechanical motion. A: Atherms are useful in a variety of rises or falls. In precise metering Atherm bellows assemblies take applications. They are commonly used applications, they can adjust advantage of the flexible, expandable in optical applications because of the orifice openings so that the mass flow of nature of precision electroformed metal precision required to maintain the gas or liquid is normalized independent bellows, and the steady volumetric properties of sensitive optics over the of temperature. expansion of incompressible fluids with range of operating temperatures. These assemblies provide changes in temperature. These bellows Other applications put temperature- temperature-dependent mechanical assemblies have known temperature- dependent length change to mechanical actuation without the need for dependent rates of length change use, similar to the operation of a programming or electricity. Their simple, depending upon the fluid used in the thermostat’s bimetallic strip. And robust design lets them operate through assembly. atherm assemblies can shield delicate hundreds of millions of repeatable cycles Each end of the bellows connects to systems from the effects of without drawing power or requiring system components using stock fittings temperature change.
    [Show full text]
  • Optomechanical Design of Nine Cameras for the Earth Observing
    Optomechanical Designof Nine Cameras for the Earth Observing Systems Multi-Angle Imaging Spectral Radiometer, TERRAPlatform Virginia G. Ford, Mary L. White, Eric Hochberg, and Jim McGown Jet Propulsion Laboratory California Institute of Technology ABSTRACT The Multi-Angle Imaging Spectral Radiometer (MISR) is a push-broom instrument using nine cameras to collect data at nine different angles through the atmosphere. The science goals are to monitor global atmospheric particulates, cloud movements, and vegetative changes. The camera optomechanical requirements were: to operate within specification over a temperature range of OC to 1OC; to survive a temperaturerange of -40C to 80C; to survive launch loads and on-orbit radiation; to be non- contaminating both to itself and to other instruments; and to remained aligned though the mission. Each camera has its own lens, detector, and thermal control. The lenses are refractive; thus passive thermal focus compensation and maintaining lens positioning and centering were dominant issues. Because of the number of cameras, modularity was stressed in the design. This paper will describe the final design of the cameras, the driving design considerations, and the results of qualification testing. Keywords: Optomechanicai, refractive lens, passive thermal compensation, lens positioning, MISR, lens centering Figure 1. EOS-TERRA spacecraft with the Multi-.Ugle Imaging Spectral Radiometerinstrument. The nine camera fields- of-view with four spectral wavebands are shown. 1. INTRODUCTION MISR is mounted on thc EOS-TERRA spacecraft, which will orbit around the Earth for up to a six-year mission. The spacecraft will be launched on an ATLAS IIAS rocket from Vanderberg AirforceBase - the launch is currently scheduled on August 27, 1999.
    [Show full text]
  • Design of an Optical System for a 5Th Generation, High
    Proceedings of COBEM 2009 20th International Congress of Mechanical Engineering Copyright © 2009 by ABCM November 15-20, 2009, Gramado, RS DESIGN OF AN OPTICAL SYSTEM FOR A 5TH GENERATION, HIGH PERFORMANCE, AIR-TO-AIR MISSILE, CONSIDERING THE IMAGING PERFORMANCE DEGRADATION DUE TO THE AERODYNAMIC HEATING Leite Junior, Paulo Roberto Comando Geral de Tecnologia Aeroespacial (CTA)/ Instituto de Aeronáutica e Espaço (IAE)/ Divisão de Sistemas de Defesa(ASD) DENEL Aerospace System / South Africa [email protected] Paoli, Eduardo Tadeu Mectron S.A./ DENEL Aerospace System/ South Africa [email protected] Hassmann, Carlos Henrique Gustavo Mectron S.A./ DENEL Aerospace System/ South Africa [email protected] An air-to-air missile is always submitted to extreme condition of temperature, such as a hot runway over a rain forest or desert area and dropping down to very cold conditions at high altitudes. It is evident that the optical system must be able to provide satisfactory image quality under any circumstances without causing any major degradation for the image. The influence of the aerodynamic heating for this missile flying at supersonic speed must be evaluated in respect to optical performance as well. The aerodynamic heating is defined as the rise in temperature of the air adjacent to the external surface of a missile due to compression and friction during the missile flight attached to the aircraft or launched. While it appears relatively easy to calculate the aerodynamic heating, the actual wall temperature attained is the most difficult problem, and most likely a transient one. Further factors need to be included when attempting to estimate the surface temperature of a supersonic missile, such as radiation and conduction.
    [Show full text]
  • Athermalization Techniques in Infrared Systems
    ATHERMALIZATION TECHNIQUES IN INFRARED SYSTEMS JEFFREY T DAIKER OPTI 521 DECEMBER 6, 2010 ABSTRACT A major area of concern when designing infrared systems is the defocus with temperature change due to the nature of lens materials. This tutorial describes how this defocus affects the system performance and discusses some techniques for solving this problem. The key advantages and disadvantages of each technique are identified. INTRODUCTION There is continued interest in developing high performance infrared (IR) systems which are capable of operating in harsh environments with extreme temperatures. The technique for maintaining focus of an IR system over an extended temperature range is called athermalization. The problem is quite challenging as most commonly used IR materials exhibit very large changes in refractive index with temperature, which inherently leads to changes in focal length of the system. Several techniques exist to control this effect and maintain acceptable focus over wide temperature ranges. EFFECT OF TEMPERATURE ON FOCUS Considering the simple case of a single element thin lens, the change in focal length of the lens with temperature is given by / ∆ ∆ ∆ 1 Where: = thermo‐optical coefficient of the lens dn/dT = refractive index change with temperature n = refractive index of the lens = thermal expansion coefficient (TCE) of the lens OPTI 521 – Fall 2010 Tutorial Daiker f = focal length of the lens ∆ = temperature change Further considering the simple case of this lens housing, the expansion of the housing with
    [Show full text]
  • Athermalization Techniques in Infrared Systems
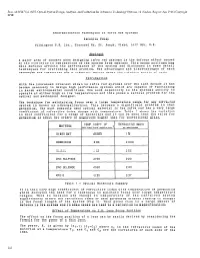
    Proc.ofSPIEVol.0655,OpticalSystemDesign,Analysis,andProductionforAdvancedTechnologySystems,ed.Fischer,Rogers(Apr1986)Copyright SPIE Athermalisation Techniques in Infra Red Systems Veronica Povey Pilkington P.E. Ltd., Glascoed Rd, St. Asaph, Clwyd, LL17 OLL, U.K. Abstract A major area of concern when designing infra red systems is the defocus effect caused by the variation in temperature of the system from ambient. This paper outlines how this defocus affects the performance of the system and discusses in some detail techniques for overcoming this problem. The advantages and disadvantages of each technique are identified and a trade-off matrix shows the relative merits of each. Introduction With the increased interest shown in infra red systems over the last decade it has become necessary to design high performance systems which are capable of functioning in harsh environmental conditions. One such capability is the systems ability to operate at either high or low temperatures and this poses a serious problem for the optical and mechanical designer. The technique for maintaining focus over a large temperature range for any infra-red system is known as athermalisation. This becomes a significant problem in that germanium, the most commonly used optical material in the infra red has a very large coefficient of refractive index change with temperature. Table 1 shows the variation in this coefficient for a range of materials and it can be seen that the value for germanium is about two orders of magnitude higher than for conventional glass. TEMP COEFF OF REFRACTIVE INDEX MATERIAL REFRACTIVE INDEX xIO-~ IO MICRONS GLASS BK7 +0025 I 51 GERMANIUM +396 4003 SILICON +I 62 238 ZINC SULPHIDE +050 220 ZINC SELENIDE +060 240 KRS-5 -235 237 Table 1 - Optical Materials Summary It is this very high coefficient of refractive index with temperature of germanium which dictates the need for a technique to maintain focus over large temperature ranges.
    [Show full text]