DOCSLIB.ORG

Study of Photometric Phase Curve: Assuming a Cellinoid Ellipsoid Shape of Asteroid (106) Dione

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Study of Photometric Phase Curve: Assuming a Cellinoid Ellipsoid Shape of Asteroid (106) Dione RAA 2017 Vol. X No. XX, 000–000 R c 2017 National Astronomical Observatories, CAS and IOP Publishing Ltd. esearch in Astronomy and http://www.raa-journal.org http://iopscience.iop.org/raa Astrophysics Study of photometric phase curve: assuming a Cellinoid ellipsoid shape of asteroid (106) Dione Yi-Bo Wang1,2,3, Xiao-Bin Wang1,3,4, Donald P. Pray5 and Ao Wang1,2,3 1 Yunnan Observatories, Chinese Academy of Sciences, Kunming 650216, China; [email protected], [email protected] 2 University of Chinese Academy of Sciences, Beijing 100049, China 3 Key Laboratory for the Structure and Evolution of Celestial Objects, Chinese Academy of Sciences, Kunming 650216, China 4 Center for Astronomical Mega-Science, Chinese Academy of Sciences, Beijing 100012, China 5 Sugarloaf Mountain Observatory, South Deerfield, MA 01373, USA Received 2017 May 9; accepted 2017 May 31 Abstract We carried out the new photometric observations of asteroid (106) Dione at three apparitions (2004, 2012 and 2015) to understand its basic physical properties. Based on a new brightness model, the new photometric observational data and the published data of (106) Dione were analyzed to characterize the morphology of Dione’s photometric phase curve. In this brightness model, Cellinoid ellipsoid shape and three-parameter (H, G1, G2) magnitude phase function system were involved. Such a model can not only solve the phase function system parameters of (106) Dione by considering an asymmetric shape of asteroid, but also can be applied to more asteroids, especially for those asteroids without enough photometric data to solve the convex shape. Using a Markov Chain Monte Carlo (MCMC) method, +0.03 +0.077 Dione’s absolute magnitude H =7.66−0.03 mag, and phase function parameters G1 =0.682−0.077 and +0.042 G2 = 0.081−0.042 were obtained. Simultaneously, a Dione’s simplistic shape, orientation of pole and rotation period were also determined. Key words: asteroids: general: photometric phase curve — asteroids: individual: (106) Dione — tech- niques: photometric; MCMC method 1 INTRODUCTION Mishchenko 1999, 2013; Belskaya & Shevchenko 2000; Muinonen et al. 2002; Oszkiewicz et al. 2012). Asteroids are thought to be the remnants of the planetes- In 1985, a semi-empirical H − G magnitude system imals related to the progenitor bodies which formed ter- (Bowell et al. 1989) was adopted as the standard magni- restrial planets and cores of giant planets. They can pro- tude system by International Astronomical Union (IAU), vide us the important clues to pristine composition of the where H and G are the absolute magnitude of an aster- solar nebula (Michel et al. 2015). oid and the slope factor, respectively. The H − G sys- Photometric phase curve, as one of the crucial phys- tem reflecting Lumme-Bowell reflectance law (Lumme ical properties of an asteroid, presents the observational & Bowell 1981), has been used to study the behavior brightness variations at the different solar phase angles of the photometric phase curve of asteroid for many (hereafter phase angle). It can also provide us the im- years. However, it cannot accurately fit the photomet- portant information on the nature of surface of an aster- ric phase curves of low-albedo and high-albedo aster- oid, such as porosity, asymmetry factor and roughness oids (Belskaya & Shevchenko 2000). Therefore, a three- (Hapke 1984, 1986, 2002; Muinonen 1994; Dlugach & parameter (H, G1, G2) magnitude phase function system 2 Y.-B. Wang, X.-B. Wang, D. P. Pray and A. Wang (Muinonen et al. 2010) was adopted as the new standard orientation of pole and shape are not obtained. In order to magnitude system in the 28th General Assembly of IAU. accurately determine the phase function system parame- This new system improves the fitting results of photomet- ters, spin parameters and Cellinoid shape of Dione, new ric phase curves for all taxonomical asteroids (Muinonen observations at three apparitions (2004, 2012 and 2015) et al. 2010; Oszkiewicz et al. 2012; Penttil¨aet al. 2016; were carried out with the 1.0-m telescope at Yunnan Shevchenko et al. 2016). The parameters G1 and G2, Observatories (IAU Observatory Code 286). to some extent, can also be used to infer the surface- Section 2 contains the observation and data reduc- material information of small objects of the solar system, tion of asteroid (106) Dione. In Section 3, we introduce especially for those distant small objects. the new brightness model and the Markov Chain Monte In order to study the photometric phase curve of the Carlo (MCMC) method. The application result of this asteroid, observational data derived in a large range of model for (106) Dione is presented in Section 4 and the phase angles are needed. However, the sufficient data are discussion is contained in Section 5. Finally, in the last difficult to obtain with the ground-based instruments in section we conclude this work. a single apparition, due to the weather condition and the observation time constraint. For the observational data 2 OBSERVATION AND DATA REDUCTION obtained during different apparitions, due to the effect of non-spherical shape of asteroid, the phase function sys- To understand the basic physical properties of (106) tem parameters will be changed with the geometries of Dione, we carried out the photometric observations with observations varying. the 1-m telescope of Yunnan Observatories in 2004, 2012 A brightness model has been used to estimate the and 2015. The photometric observational data of (106) phase function system parameters of (107) Camilla Dione in 2004 were gathered by the 1k×1k pixel PI by considering a tri-axial ellipsoid shape and the 1024TKB CCD camera with a field of view (FOV) of 6.5′ × 6.5′; the data in 2012 and 2015 were obtained by (H, G1, G2) magnitudephase function system in our pre- the 2k×2kpixel Andor DW436 CCD camera with a FOV vious work (Wang et al. 2016). However, this simple tri- ′ ′ axial ellipsoid cannot be applied appropriately to those of 7.3 × 7.3 . asteroids with the irregular shape. All the scientific images were reduced using the In this paper, we develop a new brightness model Image Reduction and Analysis Facility (IRAF) software. which can more accurately estimate the magnitude-phase Following the standard reduction process, bias and flat relation, rotation period, orientation of pole and shape of effects were corrected on the scientific images. The cos- an asteroid. In detail, we consider an asymmetric shape mic rays hinting occasionally in these images were iden- model — Cellinoid ellipsoid (Cellino et al. 1989; Lu tified by a criterion of four times of the standard devia- et al. 2014) consisting of adjacent eight octants of el- tion of sky background and then were removed. Utilizing the APPHOT task, the instrumental magnitudes of refer- lipsoid with different semi-axes (a1,a2,b1,b2,c1,c2) in this new brightness model, which allows for a better fit ence stars and target asteroid are measured by an optimal to asteroid with irregular shape. In addition, the three- aperture. Before the analysis of photometric phase curve, the parameter (H, G1, G2) magnitude phase function system is also used. instrumental magnitudes of asteroid needed to be con- We applied the new brightness model to analyze the verted into the standard photometry system (e.g. the photometric data of a main-belt asteroid (106) Dione. Landolt standard photometry system). The procedure of At present, for asteroid (106) Dione, its photometric ob- magnitude calibration contains two steps: (1) To ob- tain the transformation relation between the instrument servational data had been obtained by several groups ′ (Harris et al. 1992; Pray 2005). Harris et al. (1992) magnitude mobs and the magnitude r of the Carlsberg and Pray (2005) obtained the different rotation periods Meridian Catalogue (CMC 15) system (Mui˜nos & Evans (15 hours vs. 16.26 hours). In addition, Harris et al. 2014) by the reference stars in the observed images, (1992) firstly estimated the absolute magnitude of Dione ′ mobs = k(J − K)+ r + m0, (1) H = 7.41 mag by assuming a slope factor G = 0.09. Later, Shevchenko & Tedesco (2006) obtained its abso- where, the examined parameter k and m0 are solved by lute magnitude H = 7.66 mag by the occultation data. the linear least square method. J- and K-bands mag- However, until now, the detailed information on Dione’s nitudes are derived from 2MASS catalogue. Then, the Study of photometric phase curve: asteroid (106) Dione. 3 Table 1 Information on the New Photometric Observations of Asteroid (106) Dione Date r ∆ α filter Note (UT) (AU) (AU) (◦) 2004/11/03.8 2.684 1.830 13.1 I 1.0-m YNAO 2004/11/04.8 2.685 1.824 12.7 V,I 1.0-m YNAO 2004/11/06.9 2.687 1.810 12.0 I 1.0-m YNAO 2004/11/07.8 2.688 1.804 11.6 I 1.0-m YNAO 2004/11/08.9 2.689 1.798 11.3 I 1.0-m YNAO 2004/12/01.8 2.714 1.730 1.8 I 1.0-m YNAO 2004/12/03.8 2.716 1.731 1.0 V,I 1.0-m YNAO 2012/03/13.7 3.578 2.591 2.1 R 1.0-m YNAO 2012/03/14.7 3.579 2.590 1.9 R 1.0-m YNAO 2012/03/15.8 3.580 2.590 1.8 R 1.0-m YNAO 2012/03/17.8 3.582 2.590 1.6 R 1.0-m YNAO 2015/11/15.6 2.651 1.694 6.8 C 1.0-m YNAO 2015/11/16.6 2.651 1.698 7.2 C 1.0-m YNAO -0.25 -0.25 2004-11-08 (1.0-m) 2004-11-03 (1.0-m) -0.20 -0.20 2004-11-04 (1.0-m) 2004-12-01 (1.0-m) 2004-11-06 (1.0-m) 2004-12-03 (1.0-m) -0.15 -0.15 2004-11-07 (1.0-m) -0.10 -0.10 -0.05 -0.05 0.00 0.00 0.05 0.05 2004-12-04 (Pray 2005) 0.10 0.10 2004-12-18 (Pray 2005) RelativeMagnitude RelativeMagnitude 1981-09-20 (Harris et al.
Load more

Recommended publications
  • ~XECKDING PAGE BLANK WT FIL,,Q
    1,. ,-- ,-- ~XECKDING PAGE BLANK WT FIL,,q DYNAMICAL EVIDENCE REGARDING THE RELATIONSHIP BETWEEN ASTEROIDS AND METEORITES GEORGE W. WETHERILL Department of Temcltricrl kgnetism ~amregie~mtittition of Washington Washington, D. C. 20025 Meteorites are fragments of small solar system bodies (comets, asteroids and Apollo objects). Therefore they may be expected to provide valuable information regarding these bodies. How- ever, the identification of particular classes of meteorites with particular small bodies or classes of small bodies is at present uncertain. It is very unlikely that any significant quantity of meteoritic material is obtained from typical ac- tive comets. Relatively we1 1-studied dynamical mechanisms exist for transferring material into the vicinity of the Earth from the inner edge of the asteroid belt on an 210~-~year time scale. It seems likely that most iron meteorites are obtained in this way, and a significant yield of complementary differec- tiated meteoritic silicate material may be expected to accom- pany these differentiated iron meteorites. Insofar as data exist, photometric measurements support an association between Apollo objects and chondri tic meteorites. Because Apol lo ob- jects are in orbits which come close to the Earth, and also must be fragmented as they traverse the asteroid belt near aphel ion, there also must be a component of the meteorite flux derived from Apollo objects. Dynamical arguments favor the hypothesis that most Apollo objects are devolatilized comet resiaues. However, plausible dynamical , petrographic, and cosmogonical reasons are known which argue against the simple conclusion of this syllogism, uiz., that chondri tes are of cometary origin. Suggestions are given for future theoretical , observational, experimental investigations directed toward improving our understanding of this puzzling situation.
    [Show full text]
  • Ground-Based Visible Spectroscopy of Asteroids to Support the Development of an Unsupervised Gaia Asteroid Taxonomy A
    Ground-based visible spectroscopy of asteroids to support the development of an unsupervised Gaia asteroid taxonomy A. Cellino, Ph. Bendjoya, M. Delbo’, Laurent Galluccio, J. Gayon-Markt, P. Tanga, E.F. Tedesco To cite this version: A. Cellino, Ph. Bendjoya, M. Delbo’, Laurent Galluccio, J. Gayon-Markt, et al.. Ground-based visible spectroscopy of asteroids to support the development of an unsupervised Gaia asteroid tax- onomy. Astronomy and Astrophysics - A&A, EDP Sciences, 2020, 10.1051/0004-6361/202038246. hal-02942763 HAL Id: hal-02942763 https://hal.archives-ouvertes.fr/hal-02942763 Submitted on 12 Dec 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Astronomy & Astrophysics manuscript no. TNGspectra2ndrev c ESO 2020 July 28, 2020 Ground-based visible spectroscopy of asteroids to support development of an unsupervised Gaia asteroid taxonomy A. Cellino1, Ph. Bendjoya2, M. Delbo’3, L. Galluccio3, J. Gayon-Markt3, P. Tanga3, and E. F. Tedesco4 1 INAF, Osservatorio Astrofisico di Torino, via Osservatorio 20, 10025 Pino Torinese, Italy e-mail: [email protected] 2 Université de la Côte d’Azur - Observatoire de la Côte d’Azur, CNRS, Laboratoire Lagrange, Campus Valrose Nice, Nice Cedex 4, France e-mail: [email protected] 3 Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS, Laboratoire Lagrange, Boulevard de l’Observatoire, CS34229, 06304, Nice Cedex 4, France e-mail: [email protected], [email protected], [email protected] 4 Planetary Science Institute, Tucson, AZ, USA e-mail: [email protected] Received ..., 2020; accepted ..., 2020 ABSTRACT Context.
    [Show full text]
  • Sciences, Is the Discovery of Twenty-Two Minor Planets Commonly Known As the Watson Asteriods
    ASTRONOMY: A. O. LEUSCHNER 67 ADMISSIONS TO SICK REPORT-Concluded UNITED STATES NUMBERS opFr White Colored INTERNA- TIONAL CLASSIFICA- Mean strength..................................................... 545,518 13,150 TIONT Causes of admission to sick report Ratio perstrength1000 of mean 00-02, 07,15, 16,24- 27,29- 31,49, 57,58, 60,61, Traumatisms, others ............................... 9.14 10.04 63-65, 70-72, 74,76- 78,82- 84,97- 99 80 Sunstroke.. 0.04 0.08 Total for diseases................................. 882.51 1064.41 Total for external causes.. 91.69 90.42 Grand total................... ................ 974.19 1154.83 PERTURBATIONS AND TABLES OF THE MINOR PLANETS DISCOVERED BY JAMES C. WATSON BY ARMIN 0. LEUSCHNER BERKELEY ASTRONOMICAL DEPARTMENT, UNIVERSITY OF CALIFORNIA Read before the Academy, April 16, 1916 Among the many important contributions to Astronomical Science by James C. Watson, one of the original members of the National Academy of Sciences, is the discovery of twenty-two minor planets commonly known as the Watson asteriods. The first of these, (79) Eurynome, was discovered at Ann Arbor on September 14, 1863, and the last, (179) Klytaemnestra, on November 11, 1877, three years before his death. By his will a fund was bequeathed in trust to the National Academy of Sciences for the purpose of promoting astronomical research. One of the objects specifically designated was the construction of tables of the perturbations of the minor planets dis- covered by the testator. From the beginning Prof. Simon Newcomb was a Downloaded by guest on September 30, 2021 68 ASTRONOMY: A. O. LEUSCHNER member of the board of Watson Trustees; later he became chairman of the board, and remained in that capacity on the board until his death in 1908, being succeeded by Prof.
    [Show full text]
  • Hydrated Minerals on Asteroids: the Astronomical Record
    Hydrated Minerals on Asteroids: The Astronomical Record A. S. Rivkin, E. S. Howell, F. Vilas, and L. A. Lebofsky March 28, 2002 Corresponding Author: Andrew Rivkin MIT 54-418 77 Massachusetts Ave. Cambridge MA, 02139 [email protected] 1 1 Abstract Knowledge of the hydrated mineral inventory on the asteroids is important for deducing the origin of Earth’s water, interpreting the meteorite record, and unraveling the processes occurring during the earliest times in solar system history. Reflectance spectroscopy shows absorption features in both the 0.6-0.8 and 2.5-3.5 pm regions, which are diagnostic of or associated with hydrated minerals. Observations in those regions show that hydrated minerals are common in the mid-asteroid belt, and can be found in unex- pected spectral groupings, as well. Asteroid groups formerly associated with mineralogies assumed to have high temperature formation, such as MAand E-class asteroids, have been observed to have hydration features in their reflectance spectra. Some asteroids have apparently been heated to several hundred degrees Celsius, enough to destroy some fraction of their phyllosili- cates. Others have rotational variation suggesting that heating was uneven. We summarize this work, and present the astronomical evidence for water- and hydroxyl-bearing minerals on asteroids. 2 Introduction Extraterrestrial water and water-bearing minerals are of great importance both for understanding the formation and evolution of the solar system and for supporting future human activities in space. The presence of water is thought to be one of the necessary conditions for the formation of life as 2 we know it.
    [Show full text]
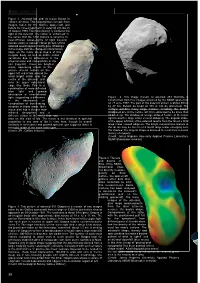
  • Iso and Asteroids
    r bulletin 108 Figure 1. Asteroid Ida and its moon Dactyl in enhanced colour. This colour picture is made from images taken by the Galileo spacecraft just before its closest approach to asteroid 243 Ida on 28 August 1993. The moon Dactyl is visible to the right of the asteroid. The colour is ‘enhanced’ in the sense that the CCD camera is sensitive to near-infrared wavelengths of light beyond human vision; a ‘natural’ colour picture of this asteroid would appear mostly grey. Shadings in the image indicate changes in illumination angle on the many steep slopes of this irregular body, as well as subtle colour variations due to differences in the physical state and composition of the soil (regolith). There are brighter areas, appearing bluish in the picture, around craters on the upper left end of Ida, around the small bright crater near the centre of the asteroid, and near the upper right-hand edge (the limb). This is a combination of more reflected blue light and greater absorption of near-infrared light, suggesting a difference Figure 2. This image mosaic of asteroid 253 Mathilde is in the abundance or constructed from four images acquired by the NEAR spacecraft composition of iron-bearing on 27 June 1997. The part of the asteroid shown is about 59 km minerals in these areas. Ida’s by 47 km. Details as small as 380 m can be discerned. The moon also has a deeper near- surface exhibits many large craters, including the deeply infrared absorption and a shadowed one at the centre, which is estimated to be more than different colour in the violet than any 10 km deep.
    [Show full text]
  • ABSTRACT Title of Dissertation: WATER in the EARLY SOLAR
    ABSTRACT Title of Dissertation: WATER IN THE EARLY SOLAR SYSTEM: INFRARED STUDIES OF AQUEOUSLY ALTERED AND MINIMALLY PROCESSED ASTEROIDS Margaret M. McAdam, Doctor of Philosophy, 2017. Dissertation directed by: Professor Jessica M. Sunshine, Department of Astronomy This thesis investigates connections between low albedo asteroids and carbonaceous chondrite meteorites using spectroscopy. Meteorites and asteroids preserve information about the early solar system including accretion processes and parent body processes active on asteroids at these early times. One process of interest is aqueous alteration. This is the chemical reaction between coaccreted water and silicates producing hydrated minerals. Some carbonaceous chondrites have experienced extensive interactions with water through this process. Since these meteorites and their parent bodies formed close to the beginning of the Solar System, these asteroids and meteorites may provide clues to the distribution, abundance and timing of water in the Solar nebula at these times. Chapter 2 of this thesis investigates the relationships between extensively aqueously altered meteorites and their visible, near and mid-infrared spectral features in a coordinated spectral-mineralogical study. Aqueous alteration is a parent body process where initially accreted anhydrous minerals are converted into hydrated minerals in the presence of coaccreted water. Using samples of meteorites with known bulk properties, it is possible to directly connect changes in mineralogy caused by aqueous alteration with spectral features. Spectral features in the mid-infrared are found to change continuously with increasing amount of hydrated minerals or degree of alteration. Building on this result, the degrees of alteration of asteroids are estimated in a survey of new asteroid data obtained from SOFIA and IRTF as well as archived the Spitzer Space Telescope data.
    [Show full text]
  • The Complete the Complete Guide to Guide to Guide to Observing Observing Lunar, Grazing and Lunar, Grazing and Asteroid Occulta
    The Complete Guide to Observing Lunar, Grazing and Asteroid Occultations Published by the International Occultation Timing Association Richard Nugent, Editor Copyright 2007 International Occultation Timing Association, Richard Nugent, Editor. All rights reserved. No part of this publication may be reproduced, distributed or copied in any manner without the written permission from the Editor in Chief. No part of this publication may be reproduced, stored in any retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning, or otherwise, except as permitted under the 1976 United States Copyright Act and with the written permission of the Editor and Publisher. Request to the Editor should be sent via email: [email protected]. While the Editor, Authors and Publisher have made their best efforts in preparing the IOTA Occultation Manual, they make no representation or warranties with respect to the accuracy and completeness regard to its contents. The Publisher, Editor and Authors specifically disclaim any implied warranties of merchantability or fitness of the material presented herein for any purpose. The advice and strategies contained herein may not be suitable for your situation and the reader and/or user assumes full responsibility for using and attempting the methods and techniques presented. Neither the publisher nor the authors shall be liable for any loss of profit or any damages, including but not limited to special, incidental, consequential, or other damages and any loss or injury. Persons are advised that occultation observations involve substantial risk and are advised to take the necessary precautions before attempting such observations. Editor in Chief: Richard Nugent Assistant Editor: Lydia Lousteaux Contributors: Trudy E.
    [Show full text]
  • The Minor Planet Bulletin Is Open to Papers on All Aspects of 6500 Kodaira (F) 9 25.5 14.8 + 5 0 Minor Planet Study
    THE MINOR PLANET BULLETIN OF THE MINOR PLANETS SECTION OF THE BULLETIN ASSOCIATION OF LUNAR AND PLANETARY OBSERVERS VOLUME 32, NUMBER 3, A.D. 2005 JULY-SEPTEMBER 45. 120 LACHESIS – A VERY SLOW ROTATOR were light-time corrected. Aspect data are listed in Table I, which also shows the (small) percentage of the lightcurve observed each Colin Bembrick night, due to the long period. Period analysis was carried out Mt Tarana Observatory using the “AVE” software (Barbera, 2004). Initial results indicated PO Box 1537, Bathurst, NSW, Australia a period close to 1.95 days and many trial phase stacks further [email protected] refined this to 1.910 days. The composite light curve is shown in Figure 1, where the assumption has been made that the two Bill Allen maxima are of approximately equal brightness. The arbitrary zero Vintage Lane Observatory phase maximum is at JD 2453077.240. 83 Vintage Lane, RD3, Blenheim, New Zealand Due to the long period, even nine nights of observations over two (Received: 17 January Revised: 12 May) weeks (less than 8 rotations) have not enabled us to cover the full phase curve. The period of 45.84 hours is the best fit to the current Minor planet 120 Lachesis appears to belong to the data. Further refinement of the period will require (probably) a group of slow rotators, with a synodic period of 45.84 ± combined effort by multiple observers – preferably at several 0.07 hours. The amplitude of the lightcurve at this longitudes. Asteroids of this size commonly have rotation rates of opposition was just over 0.2 magnitudes.
    [Show full text]
  • The V-Band Photometry of Asteroids from ASAS-SN
    Astronomy & Astrophysics manuscript no. 40759˙ArXiV © ESO 2021 July 22, 2021 V-band photometry of asteroids from ASAS-SN Finding asteroids with slow spin ? J. Hanusˇ1, O. Pejcha2, B. J. Shappee3, C. S. Kochanek4;5, K. Z. Stanek4;5, and T. W.-S. Holoien6;?? 1 Institute of Astronomy, Faculty of Mathematics and Physics, Charles University, V Holesoviˇ ckˇ ach´ 2, 18000 Prague, Czech Republic 2 Institute of Theoretical Physics, Faculty of Mathematics and Physics, Charles University, V Holesoviˇ ckˇ ach´ 2, 18000 Prague, Czech Republic 3 Institute for Astronomy, University of Hawai’i, 2680 Woodlawn Drive, Honolulu, HI 96822, USA 4 Department of Astronomy, The Ohio State University, 140 West 18th Avenue, Columbus, OH 43210, USA 5 Center for Cosmology and Astroparticle Physics, The Ohio State University, 191 W. Woodruff Avenue, Columbus, OH 43210, USA 6 The Observatories of the Carnegie Institution for Science, 813 Santa Barbara St., Pasadena, CA 91101, USA Received x-x-2021 / Accepted x-x-2021 ABSTRACT We present V-band photometry of the 20,000 brightest asteroids using data from the All-Sky Automated Survey for Supernovae (ASAS-SN) between 2012 and 2018. We were able to apply the convex inversion method to more than 5,000 asteroids with more than 60 good measurements in order to derive their sidereal rotation periods, spin axis orientations, and shape models. We derive unique spin state and shape solutions for 760 asteroids, including 163 new determinations. This corresponds to a success rate of about 15%, which is significantly higher than the success rate previously achieved using photometry from surveys.
    [Show full text]
  • MPIA Currently Employs a Staff of Approximately 160, Including 43 Scientists, 37 Junior and Visiting Scientists, Together with 80 Technical and Administrative Staff
    Max-Planck-Institut für Astronomie Heidelberg-Königstuhl Annual Report 1998 Max-Planck-Institut für Astronomie Heidelberg-Königstuhl Annual Report Das Max-Planck-Institut für Astronomie Managing Directors: Prof. Steven Beckwith (until 31. 8. 1998), Prof. Immo Appenzeller (as of 1.8.1998) Academic Members, Governing Body, Directors: Prof. Immo Appenzeller (as of 1.8.1998, temporary), Prof. Steven Beckwith, (on sabbatical leave as from 1. 9. 1998), Prof. Hans-Walter Rix (as of 1. 1. 1999). Emeritus Academic Members: Prof. Hans Elsässer, Prof. Guido Münch External Academic Members: Prof. Immo Appenzeller, Prof. Karl-Heinz Böhm, Prof. George H. Herbig Scientific Oversight Committee: Prof. R. Bender, Munich; Prof. R.-J. Dettmar, Bochum; Prof. G. Hasinger, Potsdam; Prof. P. Léna, Meudon; Prof. M. Moles Villamante, Madrid; Prof. F. Pacini, Florence; Prof. K.-H. Schmidt, Potsdam; Prof. P.A. Strittmatter, Tucson; Prof. S.D.M. White, Garching; Prof. L. Woltjer, St. Michel l’Observatoire. The MPIA currently employs a staff of approximately 160, including 43 scientists, 37 junior and visiting scientists, together with 80 technical and administrative staff. Students of the Faculty of Physics and Astronomy of the University of Heidelberg work on dissertations at degree and doctorate level in the Institute. Apprentices are con- stantly undergoing training in the Institute’s workshops. Anschrift: MPI für Astronomie, Königstuhl 17, D-69117 Heidelberg. Telephone: 0049-6221-5280, Fax: 0049-6221-528246. E-mail: [email protected], Anonymous ftp: ftp.mpia-hd.mpg.de Isophot Datacenter: [email protected]. Internet: http://www.mpia-hd.mpg.de Calar Alto Observatory Address: Centro Astronomico Hispano Aleman, Calle Jesus Durbán Remón 2/2, E-04004 Almería, Spain Telephone: 0034-50-230988, -632500, Fax: 0034-50-632504, E-mail: [email protected] Publication Information © 2000 Max-Planck-Institut für Astronomie, Heidelberg All rights reserved Printed in Germany Editors: Dr.
    [Show full text]
  • Hydrated Minerals on Asteroids 235
    Rivkin et al.: Hydrated Minerals on Asteroids 235 Hydrated Minerals on Asteroids: The Astronomical Record A. S. Rivkin Massachusetts Institute of Technology E. S. Howell Arecibo Observatory F. Vilas NASA Johnson Space Center L. A. Lebofsky University of Arizona Knowledge of the hydrated mineral inventory on the asteroids is important for deducing the origin of Earth’s water, interpreting the meteorite record, and unraveling the processes occurring during the earliest times in solar system history. Reflectance spectroscopy shows absorption features in both the 0.6–0.8 and 2.5–3.5-µm regions, which are diagnostic of or associated with hydrated minerals. Observations in those regions show that hydrated minerals are common in the mid-asteroid belt, and can be found in unexpected spectral groupings as well. Asteroid groups formerly associated with mineralogies assumed to have high-temperature formation, such as M- and E-class asteroids, have been observed to have hydration features in their reflectance spectra. Some asteroids have apparently been heated to several hundred degrees Celsius, enough to destroy some fraction of their phyllosilicates. Others have rotational variation suggesting that heating was uneven. We summarize this work, and present the astronomical evidence for water- and hydroxyl-bearing minerals on asteroids. 1. INTRODUCTION to be common. Indeed, water is found throughout the outer solar system on satellites (Clark and McCord, 1980; Clark Extraterrestrial water and water-bearing minerals are of et al., 1984), Kuiper Belt Objects (KBOs) (Brown et al., great importance both for understanding the formation and 1997), and comets (Bregman et al., 1988; Brooke et al., 1989) evolution of the solar system and for supporting future as ice, and on the planets as vapor (Larson et al., 1975; human activities in space.
    [Show full text]
  • The Planetary and Lunar Ephemeris DE 421
    IPN Progress Report 42-178 • August 15, 2009 The Planetary and Lunar Ephemeris DE 421 William M. Folkner,* James G. Williams,† and Dale H. Boggs† The planetary and lunar ephemeris DE 421 represents updated estimates of the orbits of the Moon and planets. The lunar orbit is known to submeter accuracy through fitting lunar laser ranging data. The orbits of Venus, Earth, and Mars are known to subkilometer accu- racy. Because of perturbations of the orbit of Mars by asteroids, frequent updates are needed to maintain the current accuracy into the future decade. Mercury’s orbit is determined to an accuracy of several kilometers by radar ranging. The orbits of Jupiter and Saturn are determined to accuracies of tens of kilometers as a result of spacecraft tracking and modern ground-based astrometry. The orbits of Uranus, Neptune, and Pluto are not as well deter- mined. Reprocessing of historical observations is expected to lead to improvements in their orbits in the next several years. I. Introduction The planetary and lunar ephemeris DE 421 is a significant advance over earlier ephemeri- des. Compared with DE 418, released in July 2007,1 the DE 421 ephemeris includes addi- tional data, especially range and very long baseline interferometry (VLBI) measurements of Mars spacecraft; range measurements to the European Space Agency’s Venus Express space- craft; and use of current best estimates of planetary masses in the integration process. The lunar orbit is more robust due to an expanded set of lunar geophysical solution parameters, seven additional months of laser ranging data, and complete convergence.
    [Show full text]