The First 400,000 Years…
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

1 Lecture 26
PHYS 445 Lecture 26 - Black-body radiation I 26 - 1 Lecture 26 - Black-body radiation I What's Important: · number density · energy density Text: Reif In our previous discussion of photons, we established that the mean number of photons with energy i is 1 n = (26.1) i eß i - 1 Here, the questions that we want to address about photons are: · what is their number density · what is their energy density · what is their pressure? Number density n Eq. (26.1) is written in the language of discrete states. The first thing we need to do is replace the sum by an integral over photon momentum states: 3 S i ® ò d p Of course, it isn't quite this simple because the density-of-states issue that we introduced before: for every spin state there is one phase space state for every h 3, so the proper replacement more like 3 3 3 S i ® (1/h ) ò d p ò d r The units now work: the left hand side is a number, and so is the right hand side. But this expression ignores spin - it just deals with the states in phase space. For every photon momentum, there are two ways of arranging its polarization (i.e., the orientation of its electric or magnetic field vectors): where the photon momentum vector is perpendicular to the plane. Thus, we have 3 3 3 S i ® (2/h ) ò d p ò d r. (26.2) Assuming that our system is spatially uniform, the position integral can be replaced by the volume ò d 3r = V. -

Fine-Tuning, Complexity, and Life in the Multiverse*
Fine-Tuning, Complexity, and Life in the Multiverse* Mario Livio Dept. of Physics and Astronomy, University of Nevada, Las Vegas, NV 89154, USA E-mail: [email protected] and Martin J. Rees Institute of Astronomy, University of Cambridge, Cambridge CB3 0HA, UK E-mail: [email protected] Abstract The physical processes that determine the properties of our everyday world, and of the wider cosmos, are determined by some key numbers: the ‘constants’ of micro-physics and the parameters that describe the expanding universe in which we have emerged. We identify various steps in the emergence of stars, planets and life that are dependent on these fundamental numbers, and explore how these steps might have been changed — or completely prevented — if the numbers were different. We then outline some cosmological models where physical reality is vastly more extensive than the ‘universe’ that astronomers observe (perhaps even involving many ‘big bangs’) — which could perhaps encompass domains governed by different physics. Although the concept of a multiverse is still speculative, we argue that attempts to determine whether it exists constitute a genuinely scientific endeavor. If we indeed inhabit a multiverse, then we may have to accept that there can be no explanation other than anthropic reasoning for some features our world. _______________________ *Chapter for the book Consolidation of Fine Tuning 1 Introduction At their fundamental level, phenomena in our universe can be described by certain laws—the so-called “laws of nature” — and by the values of some three dozen parameters (e.g., [1]). Those parameters specify such physical quantities as the coupling constants of the weak and strong interactions in the Standard Model of particle physics, and the dark energy density, the baryon mass per photon, and the spatial curvature in cosmology. -

Cosmology Slides
Inhomogeneous cosmologies George Ellis, University of Cape Town 27th Texas Symposium on Relativistic Astrophyiscs Dallas, Texas Thursday 12th December 9h00-9h45 • The universe is inhomogeneous on all scales except the largest • This conclusion has often been resisted by theorists who have said it could not be so (e.g. walls and large scale motions) • Most of the universe is almost empty space, punctuated by very small very high density objects (e.g. solar system) • Very non-linear: / = 1030 in this room. Models in cosmology • Static: Einstein (1917), de Sitter (1917) • Spatially homogeneous and isotropic, evolving: - Friedmann (1922), Lemaitre (1927), Robertson-Walker, Tolman, Guth • Spatially homogeneous anisotropic (Bianchi/ Kantowski-Sachs) models: - Gödel, Schücking, Thorne, Misner, Collins and Hawking,Wainwright, … • Perturbed FLRW: Lifschitz, Hawking, Sachs and Wolfe, Peebles, Bardeen, Ellis and Bruni: structure formation (linear), CMB anisotropies, lensing Spherically symmetric inhomogeneous: • LTB: Lemaître, Tolman, Bondi, Silk, Krasinski, Celerier , Bolejko,…, • Szekeres (no symmetries): Sussman, Hellaby, Ishak, … • Swiss cheese: Einstein and Strauss, Schücking, Kantowski, Dyer,… • Lindquist and Wheeler: Perreira, Clifton, … • Black holes: Schwarzschild, Kerr The key observational point is that we can only observe on the past light cone (Hoyle, Schücking, Sachs) See the diagrams of our past light cone by Mark Whittle (Virginia) 5 Expand the spatial distances to see the causal structure: light cones at ±45o. Observable Geo Data Start of universe Particle Horizon (Rindler) Spacelike singularity (Penrose). 6 The cosmological principle The CP is the foundational assumption that the Universe obeys a cosmological law: It is necessarily spatially homogeneous and isotropic (Milne 1935, Bondi 1960) Thus a priori: geometry is Robertson-Walker Weaker form: the Copernican Principle: We do not live in a special place (Weinberg 1973). -

Arxiv:Hep-Ph/9912247V1 6 Dec 1999 MGNTV COSMOLOGY IMAGINATIVE Abstract
IMAGINATIVE COSMOLOGY ROBERT H. BRANDENBERGER Physics Department, Brown University Providence, RI, 02912, USA AND JOAO˜ MAGUEIJO Theoretical Physics, The Blackett Laboratory, Imperial College Prince Consort Road, London SW7 2BZ, UK Abstract. We review1 a few off-the-beaten-track ideas in cosmology. They solve a variety of fundamental problems; also they are fun. We start with a description of non-singular dilaton cosmology. In these scenarios gravity is modified so that the Universe does not have a singular birth. We then present a variety of ideas mixing string theory and cosmology. These solve the cosmological problems usually solved by inflation, and furthermore shed light upon the issue of the number of dimensions of our Universe. We finally review several aspects of the varying speed of light theory. We show how the horizon, flatness, and cosmological constant problems may be solved in this scenario. We finally present a possible experimental test for a realization of this theory: a test in which the Supernovae results are to be combined with recent evidence for redshift dependence in the fine structure constant. arXiv:hep-ph/9912247v1 6 Dec 1999 1. Introduction In spite of their unprecedented success at providing causal theories for the origin of structure, our current models of the very early Universe, in partic- ular models of inflation and cosmic defect theories, leave several important issues unresolved and face crucial problems (see [1] for a more detailed dis- cussion). The purpose of this chapter is to present some imaginative and 1Brown preprint BROWN-HET-1198, invited lectures at the International School on Cosmology, Kish Island, Iran, Jan. -

String Theory and Pre-Big Bang Cosmology
IL NUOVO CIMENTO 38 C (2015) 160 DOI 10.1393/ncc/i2015-15160-8 Colloquia: VILASIFEST String theory and pre-big bang cosmology M. Gasperini(1)andG. Veneziano(2) (1) Dipartimento di Fisica, Universit`a di Bari - Via G. Amendola 173, 70126 Bari, Italy and INFN, Sezione di Bari - Bari, Italy (2) CERN, Theory Unit, Physics Department - CH-1211 Geneva 23, Switzerland and Coll`ege de France - 11 Place M. Berthelot, 75005 Paris, France received 11 January 2016 Summary. — In string theory, the traditional picture of a Universe that emerges from the inflation of a very small and highly curved space-time patch is a possibility, not a necessity: quite different initial conditions are possible, and not necessarily unlikely. In particular, the duality symmetries of string theory suggest scenarios in which the Universe starts inflating from an initial state characterized by very small curvature and interactions. Such a state, being gravitationally unstable, will evolve towards higher curvature and coupling, until string-size effects and loop corrections make the Universe “bounce” into a standard, decreasing-curvature regime. In such a context, the hot big bang of conventional cosmology is replaced by a “hot big bounce” in which the bouncing and heating mechanisms originate from the quan- tum production of particles in the high-curvature, large-coupling pre-bounce phase. Here we briefly summarize the main features of this inflationary scenario, proposed a quarter century ago. In its simplest version (where it represents an alternative and not a complement to standard slow-roll inflation) it can produce a viable spectrum of density perturbations, together with a tensor component characterized by a “blue” spectral index with a peak in the GHz frequency range. -
![Arxiv:1707.01004V1 [Astro-Ph.CO] 4 Jul 2017](https://docslib.b-cdn.net/cover/2069/arxiv-1707-01004v1-astro-ph-co-4-jul-2017-392069.webp)
Arxiv:1707.01004V1 [Astro-Ph.CO] 4 Jul 2017
July 5, 2017 0:15 WSPC/INSTRUCTION FILE coc2ijmpe International Journal of Modern Physics E c World Scientific Publishing Company Primordial Nucleosynthesis Alain Coc Centre de Sciences Nucl´eaires et de Sciences de la Mati`ere (CSNSM), CNRS/IN2P3, Univ. Paris-Sud, Universit´eParis–Saclay, Bˆatiment 104, F–91405 Orsay Campus, France [email protected] Elisabeth Vangioni Institut d’Astrophysique de Paris, UMR-7095 du CNRS, Universit´ePierre et Marie Curie, 98 bis bd Arago, 75014 Paris (France), Sorbonne Universit´es, Institut Lagrange de Paris, 98 bis bd Arago, 75014 Paris (France) [email protected] Received July 5, 2017 Revised Day Month Year Primordial nucleosynthesis, or big bang nucleosynthesis (BBN), is one of the three evi- dences for the big bang model, together with the expansion of the universe and the Cos- mic Microwave Background. There is a good global agreement over a range of nine orders of magnitude between abundances of 4He, D, 3He and 7Li deduced from observations, and calculated in primordial nucleosynthesis. However, there remains a yet–unexplained discrepancy of a factor ≈3, between the calculated and observed lithium primordial abundances, that has not been reduced, neither by recent nuclear physics experiments, nor by new observations. The precision in deuterium observations in cosmological clouds has recently improved dramatically, so that nuclear cross sections involved in deuterium BBN need to be known with similar precision. We will shortly discuss nuclear aspects re- lated to BBN of Li and D, BBN with non-standard neutron sources, and finally, improved sensitivity studies using Monte Carlo that can be used in other sites of nucleosynthesis. -

Big Bang Blunder Bursts the Multiverse Bubble
WORLD VIEW A personal take on events IER P P. PA P. Big Bang blunder bursts the multiverse bubble Premature hype over gravitational waves highlights gaping holes in models for the origins and evolution of the Universe, argues Paul Steinhardt. hen a team of cosmologists announced at a press world will be paying close attention. This time, acceptance will require conference in March that they had detected gravitational measurements over a range of frequencies to discriminate from fore- waves generated in the first instants after the Big Bang, the ground effects, as well as tests to rule out other sources of confusion. And Worigins of the Universe were once again major news. The reported this time, the announcements should be made after submission to jour- discovery created a worldwide sensation in the scientific community, nals and vetting by expert referees. If there must be a press conference, the media and the public at large (see Nature 507, 281–283; 2014). hopefully the scientific community and the media will demand that it According to the team at the BICEP2 South Pole telescope, the is accompanied by a complete set of documents, including details of the detection is at the 5–7 sigma level, so there is less than one chance systematic analysis and sufficient data to enable objective verification. in two million of it being a random occurrence. The results were The BICEP2 incident has also revealed a truth about inflationary the- hailed as proof of the Big Bang inflationary theory and its progeny, ory. The common view is that it is a highly predictive theory. -

Lecture 17 : the Cosmic Microwave Background
Let’s think about the early Universe… Lecture 17 : The Cosmic ! From Hubble’s observations, we know the Universe is Microwave Background expanding ! This can be understood theoretically in terms of solutions of GR equations !Discovery of the Cosmic Microwave ! Earlier in time, all the matter must have been Background (ch 14) squeezed more tightly together ! If crushed together at high enough density, the galaxies, stars, etc could not exist as we see them now -- everything must have been different! !The Hot Big Bang This week: read Chapter 12/14 in textbook 4/15/14 1 4/15/14 3 Let’s think about the early Universe… Let’s think about the early Universe… ! From Hubble’s observations, we know the Universe is ! From Hubble’s observations, we know the Universe is expanding expanding ! This can be understood theoretically in terms of solutions of ! This can be understood theoretically in terms of solutions of GR equations GR equations ! Earlier in time, all the matter must have been squeezed more tightly together ! If crushed together at high enough density, the galaxies, stars, etc could not exist as we see them now -- everything must have been different! ! What was the Universe like long, long ago? ! What were the original contents? ! What were the early conditions like? ! What physical processes occurred under those conditions? ! How did changes over time result in the contents and structure we see today? 4/15/14 2 4/15/14 4 The Poetic Version ! In a brilliant flash about fourteen billion years ago, time and matter were born in a single instant of creation. -
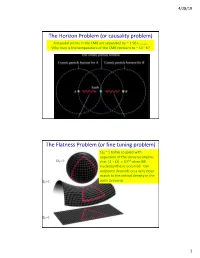
Or Causality Problem) the Flatness Problem (Or Fine Tuning Problem
4/28/19 The Horizon Problem (or causality problem) Antipodal points in the CMB are separated by ~ 1.96 rhorizon. Why then is the temperature of the CMB constant to ~ 10-5 K? The Flatness Problem (or fine tuning problem) W0 ~ 1 today coupled with expansion of the Universe implies that |1 – W| < 10-14 when BB nucleosynthesis occurred. Our existence depends on a very close match to the critical density in the early Universe 1 4/28/19 Theory of Cosmic Inflation Universe undergoes brief period of exponential expansion How Inflation Solves the Flatness Problem 2 4/28/19 Cosmic Inflation Summary Standard Big Bang theory has problems with tuning and causality Inflation (exponential expansion) solves these problems: - Causality solved by observable Universe having grown rapidly from a small region that was in causal contact before inflation - Fine tuning problems solved by the diluting effect of inflation Inflation naturally explains origin of large scale structure: - Early Universe has quantum fluctuations both in space-time itself and in the density of fields in space. Inflation expands these fluctuation in size, moving them out of causal contact with each other. Thus, large scale anisotropies are “frozen in” from which structure can form. Some kind of inflation appears to be required but the exact inflationary model not decided yet… 3 4/28/19 BAO: Baryonic Acoustic Oscillations Predict an overdensity in baryons (traced by galaxies) ~ 150 Mpc at the scale set by the distance that the baryon-photon acoustic wave could have traveled before CMB recombination 4 4/28/19 Curves are different models of Wm A measure of clustering of SDSS Galaxies of clustering A measure Eisenstein et al. -

DARK AGES of the Universe the DARK AGES of the Universe Astronomers Are Trying to fill in the Blank Pages in Our Photo Album of the Infant Universe by Abraham Loeb
THE DARK AGES of the Universe THE DARK AGES of the Universe Astronomers are trying to fill in the blank pages in our photo album of the infant universe By Abraham Loeb W hen I look up into the sky at night, I often wonder whether we humans are too preoccupied with ourselves. There is much more to the universe than meets the eye on earth. As an astrophysicist I have the privilege of being paid to think about it, and it puts things in perspective for me. There are things that I would otherwise be bothered by—my own death, for example. Everyone will die sometime, but when I see the universe as a whole, it gives me a sense of longevity. I do not care so much about myself as I would otherwise, because of the big picture. Cosmologists are addressing some of the fundamental questions that people attempted to resolve over the centuries through philosophical thinking, but we are doing so based on systematic observation and a quantitative methodology. Perhaps the greatest triumph of the past century has been a model of the uni- verse that is supported by a large body of data. The value of such a model to our society is sometimes underappreciated. When I open the daily newspaper as part of my morning routine, I often see lengthy de- scriptions of conflicts between people about borders, possessions or liberties. Today’s news is often forgotten a few days later. But when one opens ancient texts that have appealed to a broad audience over a longer period of time, such as the Bible, what does one often find in the opening chap- ter? A discussion of how the constituents of the universe—light, stars, life—were created. -

Measurement of the Cosmic Microwave Background Radiation at 19 Ghz
Measurement of the Cosmic Microwave Background Radiation at 19 GHz 1 Introduction Measurements of the Cosmic Microwave Background (CMB) radiation dominate modern experimental cosmology: there is no greater source of information about the early universe, and no other single discovery has had a greater impact on the theories of the formation of the cosmos. Observation of the CMB confirmed the Big Bang model of the origin of our universe and gave us a look into the distant past, long before the formation of the very first stars and galaxies. In this lab, we seek to recreate this founding pillar of modern physics. The experiment consists of a temperature measurement of the CMB, which is actually “light” left over from the Big Bang. A radiometer is used to measure the intensity of the sky signal at 19 GHz from the roof of the physics building. A specially designed horn antenna allows you to observe microwave noise from isolated patches of sky, without interference from the relatively hot (and high noise) ground. The radiometer amplifies the power from the horn by a factor of a billion. You will calibrate the radiometer to reduce systematic effects: a cryogenically cooled reference load is periodically measured to catch changes in the gain of the amplifier circuit over time. 2 Overview 2.1 History The first observation of the CMB occurred at the Crawford Hill NJ location of Bell Labs in 1965. Arno Penzias and Robert Wilson, intending to do research in radio astronomy at 21 cm wavelength using a special horn antenna designed for satellite communications, noticed a background noise signal in all of their radiometric measurements. -

Black Body Radiation
BLACK BODY RADIATION hemispherical Stefan-Boltzmann law This law states that the energy radiated from a black body is proportional to the fourth power of the absolute temperature. Wien Displacement Law FormulaThe Wien's Displacement Law provides the wavelength where the spectral radiance has maximum value. This law states that the black body radiation curve for different temperatures peaks at a wavelength inversely proportional to the temperature. Maximum wavelength = Wien's displacement constant / Temperature The equation is: λmax= b/T Where: λmax: The peak of the wavelength b: Wien's displacement constant. (2.9*10(−3) m K) T: Absolute Temperature in Kelvin. Emissive power The value of the Stefan-Boltzmann constant is approximately 5.67 x 10 -8 watt per meter squared per kelvin to the fourth (W · m -2 · K -4 ). If the radiation emitted normal to the surface and the energy density of radiation is u, then emissive power of the surface E=c u If the radiation is diffuse Emitted uniformly in all directions 1 E= 푐푢 4 Thermal radiation exerts pressure on the surface on which they are Incident. If the intensity of directed beam of radiations incident normally to The surface is I 퐼 Then Pressure P=u= 푐 If the radiation is diffused 1 P= 푢 3 The value of the constant is approximately 1.366 kilowatts per square metre. When the emissivity of non-black surface is constant at all temperatures and throughout the entire range of wavelength, the surface is called Gray Body. PROBLEMS 1. The temperature of a person’s skin is 350 C.