DOCSLIB.ORG

Radio Antennas, Feed Horns, and Front-End Receivers

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Radio Antennas, Feed Horns, and Front-End Receivers Radio Antennas, Feed Horns, and Front-End Receivers Bill Petrachenko, NRCan EGU and IVS Training School on VLBI for Geodesy and Astrometry March 2-5, 2013 Aalto University, Espoo, Finland Radiation Basics – Power Flux Density -2 -1 Spectral Power Flux Density, Sf (Wm H ), is the power per unit bandwidth at frequency, f, that passes through unit area. [Subscipt f indicates spectral density, i.e. that the parameter is a function of frequency and expessed per unit bandwidth (Hz-1)] Sf can be used to express power in bandwidth, δ f , passing through area, δ A , i.e.: P = S f ⋅δA⋅δf Sf is the most commonly used parameter to characterize the strength of a source; it is often referred to simply as the Flux Density of the source. Because the typical flux of a radio source is very small, a unit of flux, the Jansky, has been defined for radio astronomy: 1 Jy = 10-26Wm-2Hz-1 The power from a 1 Jy source collected in 1 GHz bandwidth by a 12 m antenna would take about 300 years to lift a 1 gm feather by 1 mm. Radiation Basics – Surface Brightness -2 -1 -1 Surface Brightness, I f (θ , φ ) (Wm Hz sr ), is the Spectral Power Flux Density, Sf, per unit solid angle (on the sky) radiating from direction, ( θ , φ ) . (aka Intensity or Specific Intensity) Because I f varies continuously with position on the sky, it is the parameter used by astronomers for mapping sources. I f is related to Sf according to S = I dΩ f ∫ f ΔΩ Radiation Basics – Brightness Temperature Source Power generated per Flux decreases as 1/R2 unit solid angle increases proportional to R2 since the since power per unit area R is diluted as the distance area of the source (in the from the source increases. solid angle) increases as the distance from the Observer source increases. These two opposing effects cancel so that I f is independent of the distance from the source and hence a property of the source itself. For a Black Body in thermal equilibrium and in the Rayleigh-Jeans limit (i.e. h ν << kT which is good for all radio frequencies) of the Plank Equation, 2 ⎛ f ⎞ 2kTB (θ,φ) I f ()θ,φ = 2kTB ()θ,φ ⎜ ⎟ = ⎝ c ⎠ λ2 where k=1.38x10-23 (m2 kg s-2 K-1) is the Boltzmann Constant Brightness Temperature, T B ( θ , φ ) , has become a proxy for I f (θ , φ ) regardless of whether or not the radiation mechanism is that of a thermal Black Body. Radiation Basics – Radiative Transfer Thermal For a Black Body, i.e. a perfect absorber, 2 Incident ⎛ f ⎞ T I f = 2kTB ⎜ ⎟ ⎝ c ⎠ (see previous page) For an imperfect absorber 2 Scattered ⎛ f ⎞ Transmitted I f < 2kTB ⎜ ⎟ ⎝ c ⎠ T I f ∝ absorption coefficient Absorption is a Lose-lose Oxygen effect: - the desired signal For the atmosphere is attenuated Imperfect absorption is - thermal noise is added why zenith atmosphere to system noise at x-band is 3°K and Water vapour not 300°K Radiation Basics - Polarization The Polarization vector is in the instantaneous direction of the E-field vector Linear Polarization Circular Polarization Random Polarization Probability of E-field direction Most geodetic VLBI sources The most efficient detection of linear and circular polarization have nearly circular distributions, signals is with a matched detector. i.e. are nearly unpolarized. Regardless of the input signal, all of the radiated power can be detected with two orthogonal detectors, either Horizontal and Vertical linear polarization or Left and Right circular polarization. With random polarization this is the only option for detecting all the power. Linear Detector Circular Detector e.g. dipole e.g. quadrature combination 90° +/- of dipole outputs Antenna Basics •ARadio antenna is a device for converting electromagnetic radiation in free space to electric current in conductors •An Antenna Pattern is the variation of power gain (or receiving efficiency) with direction. Antenna pattern: Dipole antenna Antenna pattern: Parabolic antenna • Reciprocity is the principle that an antenna pattern is the same whether the antenna is transmitting or receiving. – Transmitting antennas are generally characterized by gain – Receiving antennas are generally characterized by effective area Antenna Gain - Characterizes a Transmitting Antenna P(θ ,φ ) Antenna gain is defined as, G () θ , φ = , where Piso P()θ,φ ~ power per unit solid angle transmitted in direction, (θ,φ) P P ~ power per unit solid angle transmitted by an isotropic antenna, P = in iso iso 4π For a lossless antenna, P = P , hence G = 1 and GdΩ = 4π out in lossless ∫ Sphere An isotropic antenna is a hypothetical lossless antenna radiating uniformly in all directions, i.e. G iso ( θ , φ ) = 1 . [Note: An isotropic antenna is a useful analytic construct but cannot be built in practice.] G(θ,φ) The beam solid angle of an antenna is defined as Ω = d Ω hence A ∫ Sphere Gmax 4π ΩA = Gmax Effective Area – Characterizes a Receiving Antenna The total power received into area, A e ( θ , φ ) , and bandwidth, BW , is ⎛ S f ⎞ P()θ,φ = ⎜ ⎟Ae ()θ,φ BW Note: S includes all radiated flux. For an ⎜ 2 ⎟ ⎝ ⎠ unpolarized source, only one half the flux is received per polarized detector. Hence 2P(θ,φ) ⎛ S ⎞ ∴ A ()θ,φ = ⎜ ⎟ e the use of ⎝ 2 ⎠ in the equations. S f ⋅ BW At a particular frequency, A e ( θ , φ ) can be rewritten 2Pf (θ,φ) Ae ()θ,φ = S f -1 where Pf (WHz ) is the power received per unit frequency The noise power (per Hz) generated by a resistor at temp, T, can be written P f = kT . Pf = kT Note: It is common to use T as a proxy for Pf , especially in low power/noise situations. Average effective area Antenna Side Resistor Side Black Body cavities I T1 T2 P = A θ,φ f dΩ f ∫ e () Sphere 2 R Pf = kT 2 2kT ⎛ f ⎞ P = ⎜ ⎟ A dΩ f 2 c ∫ e ⎝ ⎠ Sphere Rayleigh-Jeans At thermodynamic equilibrium, T1=T2 and no current flows between antenna and resistor Antenna Side must equal Resistor Side 2 2kT ⎛ f ⎞ ∴ A dΩ = kT ⎜ ⎟ ∫ e 2 ⎝ c ⎠ Sphere 2 ⎛ c ⎞ 2 A dΩ = ⎜ ⎟ = λ2 λ ∫ e ⎜ ⎟ Ae = Sphere ⎝ f ⎠ 4π For an isotropic antenna λ2 A ()θ,φ = A = e e 4π Effective Area Gain From reciprocity Ae (θ,φ)∝ G(θ,φ) From earlier results λ2 A = and G =1 e 4π Combining these λ2 A ()θ,φ = G ()θ,φ = G()θ,φ ⋅ A e 4π iso This allows us to calculate the receiving pattern from the transmitting pattern and vice versa. Main beam Sidelobes High Gain Antenna (Gmax>>1) e.g. Parabolic Reflector Antenna Stray radiation It was already shown that, in a Black Body cavity, the received spectral density is I (θ,φ) P = A θ,φ f dΩ = kT f ∫ e () Sphere 2 For a high gain antenna, A e (θ , φ ) is concentrated in the main beam; hence I (θ,φ) P = A θ,φ f dΩ = kT f ∫ e () Ω−Beam 2 which implies that I f () θ , φ need only cover the main beam for this result to be true. If a source is smaller than the main beam, I Ω P = A f dΩ = kT Source f ∫ e Ω−Beam 2 ΩBeam Main beam Sidelobes High Gain Antenna (Gmax>>1) e.g. Parabolic Reflector Antenna Stray radiation Spectral Power Flux Density, Sf, Relations If the source is larger than the beam I A S Ω PReceived = A f dΩ = e f Beam f ∫ e Ω−Beam 2 2 ΩSource If the source is smaller than the beam I A S PReceived = A f dΩ = e f f ∫ e Ω−Source 2 2 Parabolic Reflector Antenna Secondary reflector (aka Sub-reflector) Sub-reflector support legs Feed Horn Antenna positioner Feed Horn Support Structure Primary reflector Pedestal (aka antenna tower) The antenna reflectors The feed horn converts concentrate incoming E-M E-M radiation in free radiation into the focal space to electrical point of the antenna. currents in a conductor. The antenna positioner points the antenna at the desired location on the sky. Aperture Illumination The ‘Feed Horn’ is itself an antenna with a power pattern that ‘illuminates’ the reflector system. Although the terminology derives from signal transmission, the feed works equally well, in a radio telescope, as a receiving element. Over-illumination: The feed pattern extends well beyond the edge of the dish. Too much ground radiation is picked up from outside the reflector. Under-illumination: The feed pattern is almost entirely within the dish. There is minimal ground pick-up but the dish appears smaller than it is. Optimal-illumination: This is the best balance between aperture illumination and ground pick-up. The power response is usually down about 10 dB (10%) at the edge of the dish. Aperture Illumination Beam Pattern The beam pattern of the antenna is the Fourier Transform of the aperture illumination (assuming that the aperture is measured in units ofλ). λ FFT Aperture illumination Beam pattern Depending on the details of the aperture illumination, the Half Power Beam Width (HPBW) is approximately λ HPBW ≈ D where D is the diameter of the reflector. The beam becomes narrower as dish becomes larger or λ becomes shorter. (λ becoming shorter is the same as the frequency becoming larger). Aperture efficiency The antenna effective area, A e , can be compared to the antenna geometric area with the ratio, η A , being the antenna efficiency, i.e. Ae =η A Ageo π where, for a circular antenna, A = D 2 .
Load more

Recommended publications
  • Corrugated Feed-Horn Arrays for Future CMB Polarization Experiments Settore Scientifico Disciplinare FIS/01
    UNIVERSITA` DEGLI STUDI DI MILANO FACOLTA` DI SCIENZE MATEMATICHE, FISICHE E NATURALI DOTTORATO DI RICERCA IN FISICA, ASTROFISICA E FISICA APPLICATA Corrugated feed-horn arrays for future CMB polarization experiments Settore Scientifico disciplinare FIS/01 Coordinatore: Prof. Marco BERSANELLI Tutore: Prof. Marco BERSANELLI Co-Tutore: Dott. Fabrizio VILLA Tesi di dottorato di: Francesco DEL TORTO Ciclo XXIV Anno Accademico 2011-2012 To my parents Introduction The actual most corroborated model of modern cosmology is the “Hot Big Bang Model”, that results in agree with the cosmological scientific discov- eries of the last 50 years. The main observational pillars that support the model are: the discovery by Edwin Hubble of the expansion of the Universe, the abundances of the primordial elements and the discovery of the Cosmic Microwave Background (CMB) radiation. In 1929 Edwin Hubble discovered the linear relationship in distant galax- ies between their distance and recession velocity: v = Hd. The current value for the Hubble constant is known with very high precision as 72 8 Km/sec/Mpc [1], from the measurements obtained by the Hubble Space Tele-± scope on even far distant galaxies w.r.t. to the Hubble measurements. According to the Hot Big Bang Model, in the first era of its life, the Universe was constituted by photons, electrons and protons. During this time the firsts primordial elements were produced, i.e. Helium, Deuterium, and Beryllium. The abundances of the primordial elements can be calculated with precision by the Hot Big Bang Model, resulting in good agreement with the measured abundances [2], [3]. In 1965 Arno Penzias and Robert Wilson discovered the CMB, already predicted in 1948 by George Gamow in the framework of an Hot Big Bang Model.
    [Show full text]
  • Progress Toward Corrugated Feed Horn Arrays in Silicon Abstract
    Progress Toward Corrugated Feed Horn Arrays in Silicon J. Britton,∗ K. W. Yoon, J. A. Beall, D. Becker, H. M. Cho, G. C. Hilton, M. D. Niemack, and K. D. Irwin Quantum Sensors Group, NIST, Boulder, CO 80305, USA Abstract We are developing monolithic arrays of corrugated feed horns fabricated in silicon for dual-polarization single-mode operation at 90, 145 and 220 GHz. The arrays consist of hundreds of platelet feed horns assembled from gold-coated stacks of micro- machined silicon wafers. As a first step, Au-coated Si waveguides with a circular, corrugated cross section were fabricated; their attenuation was measured to be less than 0.15 dB/cm from 80 to 110 GHz at room temperature. To ease the manufacture of horn arrays, electrolytic deposition of Au on degenerate Si without a metal seed layer was demonstrated. An apparatus for measuring the radiation pattern, optical efficiency, and spectral band-pass of prototype horns is described. Feed horn arrays made of silicon may find use in measurements of the polarization anisotropy of the cosmic microwave background radiation. Imaging detectors at millimeter wavelengths can now be built with hundreds of pixels.[1] However, parallel gains in free-space coupling optics have lagged. At NIST we are pursuing monolithic arrays of corru- gated platelet feed horns made with Si. Each layer in the stack is a Si wafer with photolithographically de- fined apertures. Once assembled and coated with Au, these horn arrays are expected to feature the same low loss, wide bandwidth, minimal side lobes and low cross- correlation as electroformed horns.[2, 3] Moreover, rel- ative to metal corrugated arrays [4], Si horn arrays are expected to have the following benefits: (a) a thermal ex- pansion matched to Si detectors, (b) lower thermal mass, and (c) a straightforward development to arrays of thou- sands of horns.
    [Show full text]
  • Resolving Interference Issues at Satellite Ground Stations
    Application Note Resolving Interference Issues at Satellite Ground Stations Introduction RF interference represents the single largest impact to robust satellite operation performance. Interference issues result in significant costs for the satellite operator due to loss of income when the signal is interrupted. Additional costs are also encountered to debug and fix communications problems. These issues also exert a price in terms of reputation for the satellite operator. According to an earlier survey by the Satellite Interference Reduction Group (SIRG), 93% of satellite operator respondents suffer from satellite interference at least once a year. More than half experience interference at least once per month, while 17% see interference continuously in their day-to-day operations. Over 500 satellite operators responded to this survey. Satellite Communications Overview Satellite earth stations form the ground segment of satellite communications. They contain one or more satellite antennas tuned to various frequency bands. Satellites are used for telephony, data, backhaul, broadcast, community antenna television (CATV), internet, and other services. Depending on the application, each satellite system may be receive only or constructed for both transmit and receive operations. A typical earth station is shown in figure 1. Figure 1. Satellite Earth Station Each satellite antenna system is composed of the antenna itself (parabola dish) along with various RF components for signal processing. The RF components comprise the satellite feed system. The feed system receives/transmits the signal from the dish to a horn antenna located on the feed network. The location of the receiver feed system can be seen in figure 2. The satellite signal is reflected from the parabolic surface and concentrated at the focus position.
    [Show full text]
  • Development of Conical Horn Feed for Reflector Antenna
    International Journal of Engineering and Technology Vol. 1, No. 1, April, 2009 1793-8236 Development of Conical Horn Feed For Reflector Antenna Jagdish. M. Rathod, Member, IACSIT and Y.P.Kosta, Senior Member IEEE waveguide that provides the impedance transformation Abstract—We have designed a antenna feed with prime between the waveguide impedance and the free-space concerned that with the growing conjunctions in the mobile impedance. Horn radiators are used both as antennas in their networks, the parabolic antenna are evolving as an useful device own right, and as illuminators for reflector antennas. Horn for point to point communications where the need for high antennas are not a perfect match to the waveguide, although directivity and high power density is at the prime importance. With these needs we have designed the unusual type of feed standing wave ratios of 1.5:1 or less are achievable. The gain antenna for parabolic dish that is used for both reception and of a horn radiator is proportional to the area A of the flared transmission purpose. This different frequency band open flange), and inversely proportional to the square of the performance having horn feed, works for the parabolic wavelength [8].Following Fig.1 gives types of Horn reflector antenna. We have worked on frequency band between radiators. 4.8 GHz to 5.9 GHz for horn type of feed. Here function of the horn is to produce uniform phase front with a larger aperture than that of the waveguide and hence greater directivity. Parabolic dish antenna is the most commonly and widely used antenna in communication field mainly in satellite and radar communication.
    [Show full text]
  • POWER MICROWAVE FEED HORN C. Chang Department of Engineering
    Progress In Electromagnetics Research, PIER 101, 157{171, 2010 DESIGN AND EXPERIMENTS OF THE GW HIGH- POWER MICROWAVE FEED HORN C. Chang Department of Engineering Physics Tsinghua University Beijing, China X. X. Zhu, G. Z. Liu, J. Y. Fang, R. Z. Xiao, C. H. Chen H. Shao, J. W. Li, H. J. Huang, and Q. Y. Zhang Northwest Institute of Nuclear Technology Xi'an, Shannxi, China Z. Q. Zhang National Key Laboratory of Antennas and Microwave Technology Xidian University Xi'an, Shannxi, China Abstract|Design and optimization of high-power microwave (HPM) feed horn by combining the aperture ¯eld with radiation patterns are presented in the paper. The optimized feed horn in C band satis¯es relatively uniform aperture ¯eld, power capacity higher than 3 GW, symmetric radiation patterns, low sidelobes, and compact length. Cold tests and HPM experiments were conducted to investigate the radiation patterns and power capacity of the horn. The theoretical radiation patterns are consistent with the cold test and HPM experimental results. The power capacity of the compact HPM horn has been demonstrated by HPM experiments to be higher than 3 GW. 1. INTRODUCTION The maximum power produced by S-band resonant BWO has attained 5 GW with 100 J energy pulses [1]. With the development of narrowband multi-giga-watt HPM sources operated under vacuum, the power capacity of the HPM horn has become the major factor of Corresponding author: C. Chang ([email protected]). 158 Chang et al. limiting HPM transmission and radiation [2{5]. When the electric ¯eld amplitude at the aperture of the horn is higher than the breakdown threshold, secondary electron multipactor and plasma discharge happen at the vacuum side of the dielectric radome, leading to HPM breakdown and pulse shortening [2{5].
    [Show full text]
  • PARABOLIC DISH ANTENNAS Paul Wade N1BWT © 1994,1998
    Chapter 4 PARABOLIC DISH ANTENNAS Paul Wade N1BWT © 1994,1998 Introduction Parabolic dish antennas can provide extremely high gains at microwave frequencies. A 2- foot dish at 10 GHz can provide more than 30 dB of gain. The gain is only limited by the size of the parabolic reflector; a number of hams have dishes larger than 20 feet, and occasionally a much larger commercial dish is made available for amateur operation, like the 150-foot one at the Algonquin Radio Observatory in Ontario, used by VE3ONT for the 1993 EME Contest. These high gains are only achievable if the antennas are properly implemented, and dishes have more critical dimensions than horns and lenses. I will try to explain the fundamentals using pictures and graphics as an aid to understanding the critical areas and how to deal with them. In addition, a computer program, HDL_ANT is available for the difficult calculations and details, and to draw templates for small dishes in order to check the accuracy of the parabolic surface. Background In September 1993, I finished my 10 GHz transverter at 2 PM on the Saturday of the VHF QSO Party. After a quick checkout, I drove up Mt. Wachusett and worked four grids using a small horn antenna. However, for the 10 GHz Contest the following weekend, I wanted to have a better antenna ready. Several moderate-sized parabolic dish reflectors were available in my garage, but lacked feeds and support structures. I had thought this would be no problem, since lots of people, both amateur and commercial, use dish antennas.
    [Show full text]
  • Characteristics of Naval Fire . Control Radar
    COPY~­ CO NFI oP 1895· CHARACTERISTICS OF ,. NAVAL FIRE .CONTROL RADAR • ~ r' -i8Nfi6ENtiAt• ABUREAU OF ORDNANCE PUBLICATION ~ OP 1895 CHARACTERISTICS OF NAVAL FIRE CONTROL RADAR 12 NOVEMBER 1954 DEPARTMENT OF THE NAVY BUREAU OF ORDNANCE WASHINGTON 25, D. C. 12 November 1954 ORDNANCE PAMPHLET 1895 CHARACTERISTICS OF NAVAL FIRE CONTROL RADAR 1. Ordnance Pamphlet 1895 describes both the fundamental principles of operation of radar equipment in general and the characteristics of specific United States Naval fire control radar equipment. 2. This publication is intended for use by all personnel concerned with radar operation in general, and with the application of basic radar principles to fire control radar. 3. This publication does not supersede any existing publication. 4. This publication is El8N¥'1!HU! AitL and shall be safeguarded in ac­ cordance with the security provisions of U. S. Navy Regulations. It is for­ bidden to make extracts from or to copy this classified document, except as provided for in Article 0910 of the United States Navy Security Manual for Classified Matter. M. F. ScHoEFFEL Rear Admiral, U. S. Navy Ohief, Bureau of Ordnance .tONFIDENTIAL- 'i!Qt 'FilEt 'IJ,ll CONTENTS Chapter Page Chapte1· Page FOREWORD vi 2. Close-in Targets ............. 28 (cont) Merging Targets ............. 28 PART I-GENERAL Propeller Modulation ......... 28 1. PRINCIPLES OF THE RADAR ART 1 Geographical and Atmospheric The Echo Principle ............. 1 Conditions ................ 28 The Radio Echo at Work ......... 1 Low-flying Targets ........... 29 Radar Measurements ........... 2 Land Echoes ................ 29 Factors Affecting Radar Radar Countermeasures ...... 31 Measurements ............... 6 Spotting Surface Gun Fire ...... 32 Power and Range ............ 6 Range Spotting .............
    [Show full text]
  • Highlights of Antenna History
    ~~ IEEE COMMUNICATIONS MAGAZINE HlOHLlOHTS OF ANTENNA HISTORY JACK RAMSAY A look at the major events in the development of antennas. wires. Antenna systems similar to Edison’s were used by A. E. Dolbear in 1882 when he successfully and somewhat mysteriously succeeded in transmitting code and even speech to significant ranges, allegedly by groundconduction. NINETEENTH CENTURY WIRE ANTENNAS However, in one experiment he actually flew the first kite T is not surprising that wire antennas were inaugurated antenna.About the same time, the Irish professor, in 1842 by theinventor of wire telegraphy,Joseph C. F. Fitzgerald, calculated that a loop would radiate and that Henry, Professor’ of Natural Philosophy at Princeton, a capacitance connected to a resistor would radiate at VHF NJ. By “throwing a spark” to a circuit of wire in an (undoubtedly due to radiation from the wire connecting leads). Iupper room,Henry found that thecurrent received in a In Hertz launched,processed, and received radio 1887 H. parallel circuit in a cellar 30 ft below codd.magnetize needies. waves systematically. He used a balanced or dipole antenna With a vertical wire from his study to the roof of his house, he attachedto ’ an induction coilas a transmitter, and a detected lightning flashes 7-8 mi distant. Henry also sparked one-turn loop (rectangular) containing a sparkgap as a to a telegraph wire running from his laboratory to his house, receiver. He obtained “sympathetic resonance” by tuning the and magnetized needles in a coil attached to a parailel wire dipole with sliding spheres, and the loop by adding series 220 ft away.
    [Show full text]
  • Day 2 Session 3
    Day 2 Session 3 VSAT installation 1 1- VSAT Installation IDU Satellite receivers and routers are versatile and powerful networking platforms that receive and manage content at the network edge Modern IDUs incorporate many functions: • Routing • Encryption • Compression • Acceleration • QoS • Modem • NMS 2 1- VSAT Installation Satellite Modems Satellite modems have several options that must be considered: • 70/140 MHz or L-band IF • BUC power supply • Voltage of BUC power supply (24 or 48) 3 1- VSAT Installation Router Routers are available from a variety of manufacturers but most modern satellite modems and IDU’s incorporate this functionality internally. Modem based routers provide features not generally found in terrestrial routers: • Compatibility with encapsulators • TCP spoofing (to reduce latency and improve speed) 4 1- VSAT Installation Firewall Firewalls provide proactive threat defense that stops attacks before they spread through the network. 5 1- VSAT Installation Typical configuration 6 1- VSAT Installation Sample Hardware list The VSAT system consists of the following hardware: • The Indoor unit • The Outdoor unit assembly 7 1- VSAT Installation Sample Hardware list The outdoor unit assembly consists of: TRF FEED OMT • OMT (Orthomode Transducer) separates the transmit signal from the received signal, taking advantage of their different polarization. • TRF (Transmit Reject Filter) prevents the high power transmit signal from entering (and overloading) the receive chain. 8 1- VSAT Installation Sample Hardware list The outdoor unit assembly consists of: LNB BUC • LNB (for the receiving signal). The LNB converts the C/Ku band signal received from the satellite into an L band signal. • BUC. The BUC converts the L band signal from the IDU into a C/Ku band signal for transmission.
    [Show full text]
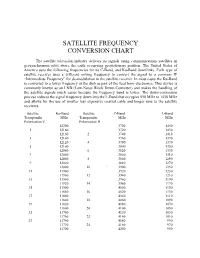
  • Satellite Frequency Conversion Chart
    SATELLITE FREQUENCY CONVERSION CHART The satellite television industry delivers its signals using communications satellites in geosynchronous orbit above the earth occupying geostationary position. The United States of America uses the following frequencies for its C-Band, and Ku-Band downlinks. Each type of satellite receiver uses a different mixing frequency to convert the signal to a common IF “Intermediate Frequency” for de-modulation in the satellite receiver. In most cases the Ku-Band is converted to a lower frequency at the dish as part of the feed horn electronics. This device is commonly known as an LNB (Low-Noise Block Down-Converter) and makes the handling of the satellite signals much easier because the frequency band is lower. The down-conversion process reduces the signal frequency down into the L-Band that occupies 950 MHz to 1450 MHz and allows for the use of smaller less expensive coaxial cable and longer runs to the satellite receivers. Satellite Ku-Band Satellite C-Band L-Band Transponder MHz Transponder MHz MHz Polarization V Polarization H 12200 3700 1450 1 12180 3720 1430 12160 2 3740 1410 3 12140 3760 1390 12120 4 3780 1370 5 12100 3800 1350 12080 6 3820 1330 7 12060 3840 1310 12040 8 3860 1290 9 12020 3880 1270 12000 10 ` 3900 1250 11 11980 3920 1230 11960 12 3940 1210 13 11940 3960 1190 11920 14 3980 1170 15 11900 4000 1150 11880 16 4020 1130 17 11860 4040 1110 11840 18 4060 1090 19 11820 4080 1070 11800 20 4100 1050 21 11780 4120 1030 11760 22 4140 1010 23 11740 4160 990 11720 24 4180 970 11700 4200 950 As you can see each of the frequencies are separated by 20 MHz, however each transponder occupies 40 MHz of bandwidth to transmit a channel.
    [Show full text]
  • Optimization Procedure for Wideband Matched Feed Design
    Optimization Procedure for Wideband Matched Feed Design Michael Forum Palvig1,2, Erik Jørgensen2, Peter Meincke2, Olav Breinbjerg1 1Department of Electrical Engineering, Electromagnetic Systems, Technical University of Denmark, Kgs. Lyngby, Denmark 2TICRA, Copenhagen, Denmark Abstract—The inherently high cross polarization of prime focus of these feeds quickly deteriorate when the frequency moves offset reflector antennas can be compensated by launching higher away from the design frequency. To improve this, the full order modes in the feed horn. Traditionally, the bandwidth of desired frequency band must be included in the design op- such systems is in the order of a few percent. We present a novel design procedure where the entire matched feed and timizations. reflector system can be efficiently optimized. This allows the design parameters of the matched feed to be directly related II. REQUIRED MODES FOR MATCHED CONDITION to the desired design goals in the secondary pattern over a specified band. Using this procedure, we present a design of a As mentioned in the previous section, the fact that the die-castable axially corrugated matched feed horn that provides required extra circular waveguide mode is TE , is usually an XPD improvement better than 7 dB over a 12% bandwidth 21 for a reflector with an f/D of 0.5. An investigation of the mode justified from the focal region fields when a plane wave is requirement for an arbitrary circular aperture feed is also incident on the reflector [1] (described in more detail in [9]). presented. The method gives a good indication of the solution to the Index Terms—matched feed, reflector antenna, horn antenna, problem, but is not strictly rigorous.
    [Show full text]
  • Fundamentals of Horn Antennas with Low Cross-Polarization Levels for Radioastronomy and Satellite Communications
    Prepared for submission to JINST Fundamentals of Horn Antennas with Low Cross-polarization Levels for Radioastronomy and Satellite Communications Javier De Miguel-Hernández,a;b;1 Roger J. Hoylanda;b aInstituto de Astrofísica de Canarias, E-38200 La Laguna, Tenerife, Spain bDepartamento de Astrofísica, Universidad de La Laguna, E-38206 La Laguna, Tenerife, Spain E-mail: [email protected] Abstract: The literature on horn antennas dedicated to radio astronomy and satellite communica- tions applications is very extensive and at times disjointed, relevant contributions being distributed as far back as from the 60’s until the present today. This work combines a compact but complete review of the different theories, methodologies and techniques used to describe corrugations and metamaterials in their application to feedhorns used in radio astronomy and satellite communica- tions along with some new work to help explain the theory in a more practical way. Starting with the hybrid-mode condition firstly corrugated horns are explained describing soft and hard boundaries and also the theory from a plasmonic optics point of view. Following this the use of metamaterials in order to design horn antennas with quasi-null cross-polarization and low E-Plane sidelobes level over an ultra-wideband is described. The objective of this work is to help to ease the learning curve of the post graduate students and young professionals dedicated to these tasks, and try to inspire the work of the senior professionals toward a new direction and approach. Keywords: Antennas, Microwave Antennas, Polarimeters, Microwave radiometers, polarization ArXiv ePrint: XXX arXiv:1910.01832v1 [astro-ph.IM] 4 Oct 2019 1Corresponding author.
    [Show full text]