DOCSLIB.ORG

Geologic Cross Sections, Maps, and Plans

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Geologic Cross Sections, Maps, and Plans CHAPTER V GEOLOGIC CROSS SECTIONS, MAPS, AND PLANS After geologic samples have been properly collected and logged, the resultant information is used to construct geologic maps and cross sections. These maps and sections will provide a graphical account of the area geology that can then be used, along with other data, to develop a site-specific description of the proposed permit and adjacent area (See Chapter VI). All such maps and sections must be prepared and certified by a qualified individual approved by the Commissioner. The following sections describe the methods of construction and the types of maps and sections that may be required. A. CONSTRUCTION AND CORRECTION TECHNIQUES Because of the lack of detailed geologic mapping in the West Virginia coal field, most cross sections and maps will have to be prepared by the applicant using information collected during the geologic sampling program. This section briefly describes methods of calculating and correcting for inclined strata. 1. Determination of Strike and Dip Strike and dip can be measured through a variety of methods, both by direct field measurement and by calculation. However, because the majority of the West Virginia coal field consists of essentially horizontal rock (<10°), the indirect method is preferable because it is not affected by minor undulations in the bedding. The easiest method of calculation is the three-point method. The three-point method utilizes three points that lie at different elevations on one bedding surface, such as the bottom of a coal seam. This bedding surface must be consistent throughout the area and be positively identified in each drill hole or outcrop. The calculation of strike and dip also requires that the distances and directions between the three points be known, along with the differences in elevation. The lateral distances can normally be determined from a topographic map and elevations from methods described in section B.l of Chapter 3. EXAMPLE Figure V- 1 illustrates a three-point problem using the elevation of the bottom of the coal seam taken from drill holes A, B, and C. The strike is found by locating a point D, where the coal would have the same elevation as drill hole B (intermediate elevation), and is on the line joining the highest and lowest coal elevations, drill holes C and A. The point D can be located by solving the equation: ___ ___ difference in elevation between A and B length of AD = length of AC x difference in elevation between A and C 72 Geologic Cross Sections, Maps, and Plans Figure V-1.-Example of Strike and Dip Calculations Using a Three-Point Problem 73 West Virginia Geologic Handbook The strike is now shown as line BD. To determine dip, a new point E is established at some distance that will create a perpendicular line to the lowest elevation point A. Once this line AE is established, dip angle can be calculated by the following equation: difference in elevation between A and E (rise) dip ∠ = inverse tangent of length of line AE (run) 2. Correction for Strike and Dip Where geologic strata are dipping off the horizontal, corrections must be made before drill hole data can be projected to the surface as a cropline. Also, drill hole data that are outside the plane or line of a geologic cross section, can be extrapolated into that cross section, if it is first adjusted for the area strike and dip. However, this extrapolation should only be used in areas of consistent stratigraphy and over relatively short distances. In areas of complex stratigraphy or structure, a fence diagram should be used instead of extrapolation techniques. The following formulas can be used to determine the vertical rise or fall of a coal seam or drill hole over a known horizontal distance. EXAMPLE 1 Where the true strike and dip are known, the rise or fall of a coal seam in any direction from a point of known elevation can be calculated using the following formula: sin x true dip angle = adjusted dip angle Where = the angle between the true strike and the direction of concern Once the adjusted dip angle is known, a simple cross section can be used to project the coal seam to its surface outcrop. Several such cross sections can be used to define the coal outcrop line. However, in cross sections using vertical exaggeration to better illustrate the local topography, the dip must be converted from degrees to slope. Once the slope is known, a slope line is projected to the surface in the same manner as described above. Figure V-2 illustrates the use of this method for the determination of coal outcrop elevations. EXAMPLE 2 For geologic cross sections where additional drill hole data are available, but not in the actual plane of the cross section, a correction factor must be determined prior to use in 74 Geologic Cross Sections, Maps, and Plans Figure V-2.-Example for Determination of Coal Outcrop Elevation 75 West Virginia Geologic Handbook the section. This correction factor is the number of feet the drill hole or strata must be raised or lowered to compensate for the area strike and dip. The correction factor can be calculated by the following formula: sin x tan x (d) = vertical correction factor in feet Where: = the angle between the true strike line and the line on which the drill hole or observation point will be moved to intercept the cross-section line or plane = the true dip angle d = the lateral distance between the drill hole or observation point to the cross-section line or plane Figure V-3 illustrates the use of this formula to calculate the amount of vertical rise which must be compensated for by the use of a drill hole located outside the cross-sectional plane. Note: The correction factor is an absolute number. To determine if this distance is added or subtracted from the actual elevations, it must be determined if the movement from the drill hole to the cross-sectional plane is up-dip or down-dip. If the movement is in the down-dip hemisphere, it is subtracted from the actual elevation; if the movement is in the up-dip hemisphere, it is added to the actual elevation. B. DRAWING DETAILS This section briefly describes the types of cross sections and maps that may be needed to adequately characterize the site geology. The actual types of drawings that might be required will be based on site-specific conditions and needs. 1. Geologic Cross Sections A geologic cross section is a diagram or drawing, made from actual observations or inferred from other evidence, of underground geologic conditions along a given line or plane of the earth's crust (Thrush et al., 1968). Each geologic cross section should depict the overburden or other material from the upper limit of disturbance down to, and including, the deeper of either the stratum immediately below the lowest coal seam to be mined or any aquifer below the lowest coal seam to be mined that may be adversely impacted by mining. For underground mining operations, a cross section should extend through the entire area of proposed workings, including the maximum depth of cover. All geologic cross sections should label all coal seams and marine zones to be disturbed using presently recognized by the West Virginia Geologic and Economic Survey. 76 Geologic Cross Sections, Maps, and Plans A cross section should be drawn from a minimum of two data points, such as drill hole sites and/or highwall/outcrop observation points. Usually, at least one cross section should be drawn as nearly parallel to the strata dip as possible, but primary consideration should always be given to an accurate portrayal of the permit area. The number of cross sections needed to depict an area may vary, depending upon the geology of the area and the size and type of mining operation. 77 West Virginia Geologic Handbook At least one cross section should be drawn to represent the areas of disturbance associated with both surface or underground mining operations. For area type surface mines, cross sections should depict both the length and width of the proposed site, and at least one cross section should Figure V-3.-Example of Correcting for Elevation Differences in Inclined Strata 78 Geologic Cross Sections, Maps, and Plans intercept any pronounced structural feature such as a fault, fold, or significant fracture zone (lineament). Each geologic cross-section should portray the nature, depth, and thickness of all strata, including coal seams and rider seams, using standard geologic terminology and symbols (See Appendix 1-3). The nature of each stratum refers to the type of material and its lithologic characteristics. A legend, and both horizontal and vertical scales (including elevations), should be indicated on the drawing, with any scale exaggerations noted. Cross sections should always include the surface topography in concert with the subsurface geology. The cross-section line should also be shown on the appropriate permit map(s). EXAMPLE 1 A site-specific geologic cross-section is provided in Figure V-4. This indicates that cross section, X-X’, is based on drill holes A, B, and C through the projected workings of a hypothetical underground mine. EXAMPLE 2 Locations of the cross section and drill holes in plan view can be shown as illustrated on the map in Figure V -5. Where sufficient ground-water information is known, a geologic cross-section should also show seasonal fluctuations in the hydraulic head. This type of information can then be used to determine the minimum elevation or relative position in the backfill, where acid- or toxic-forming materials can be disposed and remain above the postmining water table.
Load more

Recommended publications
  • Planetary Geologic Mappers Annual Meeting
    Program Lunar and Planetary Institute 3600 Bay Area Boulevard Houston TX 77058-1113 Planetary Geologic Mappers Annual Meeting June 12–14, 2018 • Knoxville, Tennessee Institutional Support Lunar and Planetary Institute Universities Space Research Association Convener Devon Burr Earth and Planetary Sciences Department, University of Tennessee Knoxville Science Organizing Committee David Williams, Chair Arizona State University Devon Burr Earth and Planetary Sciences Department, University of Tennessee Knoxville Robert Jacobsen Earth and Planetary Sciences Department, University of Tennessee Knoxville Bradley Thomson Earth and Planetary Sciences Department, University of Tennessee Knoxville Abstracts for this meeting are available via the meeting website at https://www.hou.usra.edu/meetings/pgm2018/ Abstracts can be cited as Author A. B. and Author C. D. (2018) Title of abstract. In Planetary Geologic Mappers Annual Meeting, Abstract #XXXX. LPI Contribution No. 2066, Lunar and Planetary Institute, Houston. Guide to Sessions Tuesday, June 12, 2018 9:00 a.m. Strong Hall Meeting Room Introduction and Mercury and Venus Maps 1:00 p.m. Strong Hall Meeting Room Mars Maps 5:30 p.m. Strong Hall Poster Area Poster Session: 2018 Planetary Geologic Mappers Meeting Wednesday, June 13, 2018 8:30 a.m. Strong Hall Meeting Room GIS and Planetary Mapping Techniques and Lunar Maps 1:15 p.m. Strong Hall Meeting Room Asteroid, Dwarf Planet, and Outer Planet Satellite Maps Thursday, June 14, 2018 8:30 a.m. Strong Hall Optional Field Trip to Appalachian Mountains Program Tuesday, June 12, 2018 INTRODUCTION AND MERCURY AND VENUS MAPS 9:00 a.m. Strong Hall Meeting Room Chairs: David Williams Devon Burr 9:00 a.m.
    [Show full text]
  • The Mathematics of Fels Sculptures
    THE MATHEMATICS OF FELS SCULPTURES DAVID FELS AND ANGELO B. MINGARELLI Abstract. We give a purely mathematical interpretation and construction of sculptures rendered by one of the authors, known herein as Fels sculptures. We also show that the mathematical framework underlying Ferguson's sculpture, The Ariadne Torus, may be considered a special case of the more general constructions presented here. More general discussions are also presented about the creation of such sculptures whether they be virtual or in higher dimensional space. Introduction Sculptors manifest ideas as material objects. We use a system wherein an idea is symbolized as a solid, governed by a set of rules, such that the sculpture is the expressed material result of applying rules to symbols. The underlying set of rules, being mathematical in nature, may thus lead to enormous abstraction and although sculptures are generally thought of as three dimensional objects, they can be created in four and higher dimensional (unseen) spaces with various projections leading to new and pleasant three dimensional sculptures. The interplay of mathematics and the arts has, of course, a very long and old history and we cannot begin to elaborate on this matter here. Recently however, the problem of creating mathematical programs for the construction of ribbed sculptures by Charles Perry was considered in [3]. For an insightful paper on topological tori leading to abstract art see also [5]. Spiral and twirling sculptures were analysed and constructed in [1]. This paper deals with a technique for sculpting works mostly based on wood (but not necessarily restricted to it) using abstract ideas based on twirls and tori, though again, not limited to them.
    [Show full text]
  • Lesson 4–How to Read a Topographic Map
    Lesson 4–How to Read a Topographic Map Key teaching points Suggestions for teaching Ask students to answer these ques- this lesson (3, 35-minute sessions) tions and fill in their answers on A topographic map is a representa- Activity Sheet #4: tion of a three-dimensional surface on On the poster is a topographic map a flat piece of paper. The digital eleva- of Salt Lake City. This lesson will help Which is higher, hill A or hill B? tion model on the poster is helpful in students learn how to read that map. (Answer: hill B) understanding topographic maps. Learning to use a topographic map is a difficult skill, because it requires stu- Which is steeper, hill A or hill B? Contour lines, sometimes called "level dents to visualize a three-dimensional (Answer: hill B) lines," join points of equal elevation. surface from a flat piece of paper. The closer together the contour lines Students need both practice and imag- 3. Compare a topographic map to a picture of the same place. Now have appear on a topographic map, the ination to learn to visualize hills and steeper the slope (assuming constant valleys from the contour lines on a the students look at the topographic of the same two hills. Say, "The contour intervals). topographic map. map lines you see on this map are called contour lines. Can you see why they Topographic maps have a variety of A digital terrain model of Salt Lake City uses, from planning the best route for is shown on the poster.
    [Show full text]
  • Survey of India Department of Science & Technology Rashtriya Manchitran Niti NATIONAL MAP POLICY 1
    Survey of India Department of Science & Technology Rashtriya Manchitran Niti NATIONAL MAP POLICY 1. PREAMBLE All socio-economic developmental activities, conservation of natural resources, planning for disaster mitigation and infrastructure development require high quality spatial data. The advancements in digital technologies have now made it possible to use diverse spatial databases in an integrated manner. The responsibility for producing, maintaining and disseminating the topographic map database of the whole country, which is the foundation of all spatial data vests with the Survey of India (SOI). Recently, SOI has been mandated to take a leadership role in liberalizing access of spatial data to user groups without jeopardizing national security. To perform this role, the policy on dissemination of maps and spatial data needs to be clearly stated. 2. OBJECTIVES • To provide, maintain and allow access and make available the National Topographic Database (NTDB) of the SOI conforming to national standards. • To promote the use of geospatial knowledge and intelligence through partnerships and other mechanisms by all sections of the society and work towards a knowledge-based society. 3. TWO SERIES OF MAPS To ensure that in the furtherance of this policy, national security objectives are fully safeguarded, it has been decided that there will be two series of maps namely (a) Defence Series Maps (DSMs)- These will be the topographical maps (on Everest/WGS-84 Datum and Polyconic/UTM Projection) on various scales (with heights, contours and full content without dilution of accuracy). These will mainly cater for defence and national security requirements. This series of maps (in analogue or digital forms) for the entire country will be classified, as appropriate, and the guidelines regarding their use will be formulated by the Ministry of Defence.
    [Show full text]
  • Paleoproterozoic Tectonic Evolution of the Trans-North China Orogen: Toward a Comprehensive Model
    Paleoproterozoic tectonic evolution of the Trans-North China Orogen: toward a comprehensive model. Pierre Trap, Michel Faure, Wei Lin, Nicole Le Breton, Patrick Monié To cite this version: Pierre Trap, Michel Faure, Wei Lin, Nicole Le Breton, Patrick Monié. Paleoproterozoic tectonic evolution of the Trans-North China Orogen: toward a comprehensive model.. Precambrian Research, Elsevier, 2012, 222-223, pp.191-211. 10.1016/j.precamres.2011.09.008. insu-00628119 HAL Id: insu-00628119 https://hal-insu.archives-ouvertes.fr/insu-00628119 Submitted on 2 Jan 2012 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Paleoproterozoic tectonic evolution of the Trans-North China Orogen: Toward a comprehensive model Pierre Trapa, Michel Faureb, Wei Linc, Nicole Le Bretonb, Patrick Moniéd UMR-CNRS 6249 Chrono-Environnement, Université de Franche-Comté, 16 route de Gray a 25030 Besançon Cedex, France Institut des Sciences de la Terre d‟Orléans, CNRS, Université d‟Orléans (UMR 6113), b 45071 Orléans Cedex 2, France State Key Laboratory of Lithosphere Evolution, Institute of Geology and Geophysics, c Chinese Academy of Sciences, Beijing 100029, China Géosciences Montpellier, UMR CNRS 5243, Université Montpellier II, 34095 Montpellier d Cedex 5, France Abstract In this contribution we present a reconstruction of the overall lithotectonic architecture, from inner zones to external ones, of the Paleoproterozoic Trans-North China Orogen, within the North China Craton.
    [Show full text]
  • Dairy Syncline Mine Project Record of Decision
    United States Department of Agriculture U.S. Forest Service Caribou-Targhee National Forest Final Record of Decision Dairy Syncline Mine Project, Caribou County, Idaho April 2020 Forest Service – Caribou-Targhee National Forest – April 2020 In accordance with Federal civil rights law and U.S. Department of Agriculture (USDA) civil rights regulations and policies, the USDA, its Agencies, offices, and employees, and institutions participating in or administering USDA programs are prohibited from discriminating based on race, color, national origin, religion, sex, gender identity (including gender expression), sexual orientation, disability, age, marital status, family/parental status, income derived from a public assistance program, political beliefs, or reprisal or retaliation for prior civil rights activity, in any program or activity conducted or funded by USDA (not all bases apply to all programs). Remedies and complaint filing deadlines vary by program or incident. Persons with disabilities who require alternative means of communication for program information (e.g., Braille, large print, audiotape, American Sign Language, etc.) should contact the responsible Agency or USDA’s TARGET Center at (202) 720-2600 (voice and TTY) or contact USDA through the Federal Relay Service at (800) 877-8339. Additionally, program information may be made available in languages other than English. To file a program discrimination complaint, complete the USDA Program Discrimination Complaint Form, AD- 3027, found online at http://www.ascr.usda.gov/complaint_filing_cust.html and at any USDA office or write a letter addressed to USDA and provide in the letter all of the information requested in the form. To request a copy of the complaint form, call (866) 632-9992.
    [Show full text]
  • Lab 7: Relative Dating and Geological Time
    LAB 7: RELATIVE DATING AND GEOLOGICAL TIME Lab Structure Synchronous lab work Yes – virtual office hours available Asynchronous lab work Yes Lab group meeting No Quiz None – Test 2 this week Recommended additional work None Required materials Pencil Learning Objectives After carefully reading this chapter, completing the exercises within it, and answering the questions at the end, you should be able to: • Apply basic geological principles to the determination of the relative ages of rocks. • Explain the difference between relative and absolute age-dating techniques. • Summarize the history of the geological time scale and the relationships between eons, eras, periods, and epochs. • Understand the importance and significance of unconformities. • Explain why an understanding of geological time is critical to both geologists and the general public. Key Terms • Eon • Original horizontality • Era • Cross-cutting • Period • Inclusions • Relative dating • Faunal succession • Absolute dating • Unconformity • Isotopic dating • Angular unconformity • Stratigraphy • Disconformity • Strata • Nonconformity • Superposition • Paraconformity Time is the dimension that sets geology apart from most other sciences. Geological time is vast, and Earth has changed enough over that time that some of the rock types that formed in the past could not form Lab 7: Relative Dating and Geological Time | 181 today. Furthermore, as we’ve discussed, even though most geological processes are very, very slow, the vast amount of time that has passed has allowed for the formation of extraordinary geological features, as shown in Figure 7.0.1. Figure 7.0.1: Arizona’s Grand Canyon is an icon for geological time; 1,450 million years are represented by this photo.
    [Show full text]
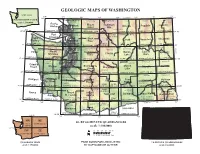
  • Geologic Maps of Washington
    GEOLOGIC MAPS OF WASHINGTON DGER GM-53 124° 117° 123° 122° 121° 120° CANADA 119° 118° 49° 49° WASHINGTON STATE PEND DGER OFR 2000-5 WHATCOM DGER OFR 90-5 USA FERRY (scale 1:500,000) OREILLE Roche Mount Bellingham Robinson Oroville Republic Colville Harbor Baker Mtn 125° OKANOGAN DGER OFR 2003-17 48°30 USGS Map I-2660 DGER OFR 90-10 DGER OFR 90-13 48°30 CANADA DGER OFR 90-11 SAN USA Port JUAN SKAGIT DGER DGER OFR 90-12 ISLAND OFR 90-9 Cape Angeles Port Sauk Nespelem Chewelah Flattery Townsend River Twisp Omak USGS Map I-1198F DGER OFR 2003-5 DGER OFR 2003-6 DGER DGER OFR 90-14 48° USGS Map I-1198G USGS Map I -2592 OFR 95-3 DGER OFR 90-16 48° CLALLAM USGS OFR 93-233 STEVENS IDAHO SNOHOMISH DOUGLAS JEFFERSON USGS OFR 91-147 CHELAN Mount Coulee Forks Seattle Skykomish Banks Spokane Olympus River Chelan Lake Dam DGER OFR 2000-4 DGER OFR 2003-4 DGER OFR 90-17 47°30 KITSAP USGS Map I-1963 USGS Map I-1661 DGER OFR 90-6 DGER OFR 90-15 47°30 GRAYS GIS data only KING LINCOLN SPOKANE Copalis HARBOR GRANT Snoqualmie Moses Beach Shelton Tacoma Wenatchee Ritzville Rosalia MASON Pass Lake DGER OFR 2003-16 KITTITAS DGER OFR 2003-15 47° DGER OFR 87-3 USGS Map I-2538 USGS Map I-1311 DGER OFR 90-1 DGER OFR 90-2 DGER OFR 90-7 47° WHITMAN PIERCE ADAMS THURSTON Westport Chehalis Mount Priest Pullman River Centralia Yakima Connell LEWIS Rainier Rapids FRANKLIN DGER DGER OFR 87-8 DGER OFR 87-8 DGER 46°30 DGER OFR 87-11 DGER OFR 87-16 OFR 86-4 OFR 94-12 DGER OFR 94-13 DGER OFR 94-14 DGER OFR 94-6 46°30 PACIFIC GARFIELD YAKIMA DGER COLUMBIA OFR 86-3 BENTON Ilwaco WAHKIAKUM Mount Clarkston Mount Richland Walla Walla Astoria St.
    [Show full text]
  • Geomorphology, Stratigraphy, and Paleohydrology of the Aeolis Dorsa Region, Mars, with Insights from Modern and Ancient Terrestrial Analogs
    University of Tennessee, Knoxville TRACE: Tennessee Research and Creative Exchange Doctoral Dissertations Graduate School 12-2016 Geomorphology, Stratigraphy, and Paleohydrology of the Aeolis Dorsa region, Mars, with Insights from Modern and Ancient Terrestrial Analogs Robert Eric Jacobsen II University of Tennessee, Knoxville, [email protected] Follow this and additional works at: https://trace.tennessee.edu/utk_graddiss Part of the Geology Commons Recommended Citation Jacobsen, Robert Eric II, "Geomorphology, Stratigraphy, and Paleohydrology of the Aeolis Dorsa region, Mars, with Insights from Modern and Ancient Terrestrial Analogs. " PhD diss., University of Tennessee, 2016. https://trace.tennessee.edu/utk_graddiss/4098 This Dissertation is brought to you for free and open access by the Graduate School at TRACE: Tennessee Research and Creative Exchange. It has been accepted for inclusion in Doctoral Dissertations by an authorized administrator of TRACE: Tennessee Research and Creative Exchange. For more information, please contact [email protected]. To the Graduate Council: I am submitting herewith a dissertation written by Robert Eric Jacobsen II entitled "Geomorphology, Stratigraphy, and Paleohydrology of the Aeolis Dorsa region, Mars, with Insights from Modern and Ancient Terrestrial Analogs." I have examined the final electronic copy of this dissertation for form and content and recommend that it be accepted in partial fulfillment of the equirr ements for the degree of Doctor of Philosophy, with a major in Geology. Devon M. Burr,
    [Show full text]
  • Sculptures in S3
    Sculptures in S3 Saul Schleimer and Henry Segerman∗ Abstract We describe the construction of a number of sculptures. Each is based on a geometric design native to the three- sphere: the unit sphere in four-dimensional space. Via stereographic projection, we transfer the design to three- dimensional space. All of the sculptures are then fabricated by the 3D printing service Shapeways. 1 Introduction The three-sphere, denoted S3, is a three-dimensional analog of the ordinary two-dimensional sphere, S2. In n+ general, the n–dimensional sphere is a subset of R 1 as follows: n n+1 2 2 2 S = f(x0;x1;:::;xn) 2 R j x0 + x1 + ··· + xn = 1g: Thus S2 can be seen as the usual unit sphere in R3. Visualising objects in dimensions higher than three is non-trivial. However for S3 we can use stereographic projection to reduce the dimension from four to three. n n n Let N = (0;:::;0;1) be the north pole of S . We define stereographic projection r : S − fNg ! R by x0 x1 xn−1 r(x0;x1;:::;xn) = ; ;:::; : 1 − xn 1 − xn 1 − xn See [1, page 27]. Figure 1a displays the one-dimensional case; this is also a cross-section of the n– dimensional case. For any point (x;y) 2 S1 − fNg draw the straight line L between N and (x;y). Then L meets R1 at a single point; this is r(x;y). N x 1−y (x;y) (a) Stereographic projection from S1 − (b) Two-dimensional stereographic projection applied to the Earth.
    [Show full text]
  • US Topo Map Users Guide
    US Topo Map Users Guide April 2018. Based on Adobe Reader XI version 11.0.20 (Minor updates and corrections, November 2017.) April 2018 Updates Based on Adobe Reader DC version 2018.009.20050 In 2017, US Topo production systems were redesigned. This system change has few impacts on the design and appearance of US Topo maps, but does affect the geospatial characteristics. The previous version of this Users Guide is frozen in its current form, and applies to US Topo maps created The previous version of this Users Guide, which before approximately June 2017 and to all HTMC applies to US Topo maps created before June maps. The document you are now reading applies 2017 and to all HTMC maps, is linked from to US Topo maps created after June 2017, and https://nationalmap.gov/ustopo will be maintained into the future. US Topo maps are the current generation of USGS topographic maps. The first of these maps were published in 2009. They are modeled on the legacy 7.5-minute series of the mid-20th century, but unlike traditional topographic maps they are mass produced from GIS databases, and are published as PDF documents instead of as paper maps. US Topo maps include base data from The National Map and other sources, including roads, hydrography, contours, boundaries, woodland cover, structures, geographic names, an aerial photo image, Federal land boundaries, and shaded relief. For more information see the project web page at https://nationalmap.gov/ustopo. The Historical Topographic Map Collection (HTMC) includes all editions and all scales of USGS standard topographic quadrangle maps originally published as paper maps in the period 1884-2006.
    [Show full text]
  • Chapter 13.2: Topographic Maps 1
    Chapter 13.2: Topographic Maps 1 A map is a model or representation of objects and terrain in the actual environment. There are numerous types of maps. Some of the types of maps include mental, planimetric, topographic, and even treasure maps. The concept of mapping was introduced in the section using natural features. Maps are created for numerous purposes. A treasure map is used to find the buried treasure. Topographic maps were originally used for military purposes. Today, they have been used for planning and recreational purposes. Although other types of maps are mentioned, the primary focus of this section is on topographic maps. Types of Maps Mental Maps – The mind makes mental maps all the time. You drive to the grocery store. You turn right onto the boulevard. You identify a street sign, building or other landmark and know where this is where you turn. You have made a mental map. This was discussed under using natural features. Planimetric Maps – A planimetric map is a two dimensional representation of objects in the environment. Generally, planimetric maps do not include topographic representation. Road maps, Rand McNally ® and GoogleMaps ® (not GoogleEarth) are examples of planimetric maps. Topographic Maps – Topographic maps show elevation or three-dimensional topography two dimensionally. Topographic maps use contour lines to show elevation. A chart refers to a nautical chart. Nautical charts are topographic maps in reverse. Rather than giving elevation, they provide equal levels of water depth. Topographic Maps Topographic maps show elevation or three-dimensional topography two dimensionally. Topographic maps use contour lines to show elevation.
    [Show full text]