Bernoulli Runs Using 'Book Cricket' to Evaluate Cricketers
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Captain Cool: the MS Dhoni Story
Captain Cool The MS Dhoni Story GULU Ezekiel is one of India’s best known sports writers and authors with nearly forty years of experience in print, TV, radio and internet. He has previously been Sports Editor at Asian Age, NDTV and indya.com and is the author of over a dozen sports books on cricket, the Olympics and table tennis. Gulu has also contributed extensively to sports books published from India, England and Australia and has written for over a hundred publications worldwide since his first article was published in 1980. Based in New Delhi from 1991, in August 2001 Gulu launched GE Features, a features and syndication service which has syndicated columns by Sir Richard Hadlee and Jacques Kallis (cricket) Mahesh Bhupathi (tennis) and Ajit Pal Singh (hockey) among others. He is also a familiar face on TV where he is a guest expert on numerous Indian news channels as well as on foreign channels and radio stations. This is his first book for Westland Limited and is the fourth revised and updated edition of the book first published in September 2008 and follows the third edition released in September 2013. Website: www.guluzekiel.com Twitter: @gulu1959 First Published by Westland Publications Private Limited in 2008 61, 2nd Floor, Silverline Building, Alapakkam Main Road, Maduravoyal, Chennai 600095 Westland and the Westland logo are the trademarks of Westland Publications Private Limited, or its affiliates. Text Copyright © Gulu Ezekiel, 2008 ISBN: 9788193655641 The views and opinions expressed in this work are the author’s own and the facts are as reported by him, and the publisher is in no way liable for the same. -

History of Men Test Cricket: an Overview Received: 14-11-2020
International Journal of Physiology, Nutrition and Physical Education 2021; 6(1): 174-178 ISSN: 2456-0057 IJPNPE 2021; 6(1): 174-178 © 2021 IJPNPE History of men test cricket: An overview www.journalofsports.com Received: 14-11-2020 Accepted: 28-12-2020 Sachin Prakash and Dr. Sandeep Bhalla Sachin Prakash Ph.D., Research Scholar, Abstract Department of Physical The concept of Test cricket came from First-Class matches, which were played in the 18th century. In the Education, Indira Gandhi TMS 19th century, it was James Lillywhite, who led England to tour Australia for a two-match series. The first University, Ziro, Arunachal official Test was played from March 15 in 1877. The first-ever Test was played with four balls per over. Pradesh, India While it was a timeless match, it got over within four days. The first notable change in the format came in 1889 when the over was increased to a five-ball, followed by the regular six-ball over in 1900. While Dr. Sandeep Bhalla the first 100 Tests were played as timeless matches, it was since 1950 when four-day and five-day Tests Director - Sports & Physical were introduced. The Test Rankings was introduced in 2003, while 2019 saw the introduction of the Education Department, Indira World Test Championship. Traditionally, Test cricket has been played using the red ball, as it is easier to Gandhi TMS University, Ziro, spot during the day. The most revolutionary change in Test cricket has been the introduction of Day- Arunachal Pradesh, India Night Tests. Since 2015, a total of 11 such Tests have been played, which three more scheduled. -

Tournament Rules Match Rules Net Run Rate
Tournament Rules - Only employees nominated by member AMCs holding valid employment card shall be allowed to participate. - Organizing committee is providing all teams with 15 color kits. No one will be allowed to wear any other kit. Extra kits (on request) would cost PKR 2,000 per kit. Teams may give names of maximum 18 players. - The tournament will consist of 12 teams in total, divided in 2 groups with each team playing 5 group matches. - At the end of the league matches, top 2 teams from each group will qualify for the semi-finals. - Points shall be awarded on the following system: win/walkover (3pts), tie/washout (1pt), lost (0pts). - In case the points are equal, the team with better net run rate (NRR) will qualify for the semi- finals (the formula is given below). - The reporting time for the morning match will be 9:00am sharp (toss at 9:15am and match would start at 9:30am) and for the afternoon match the reporting time will be 1:00pm sharp (toss at 1:15pm and match would start at 1:30pm). - Walkover will be awarded in the event if a team (minimum of 7 players) fails to appear within 30 minutes of the scheduled time of the allotted time. - In the case of a tie in a knockout match, the result will be decided by a super-over. - The team's captain will have the responsibility of maintaining discipline and healthy atmosphere during the matches, any grievances should be brought to committee's notice by the captain only. -
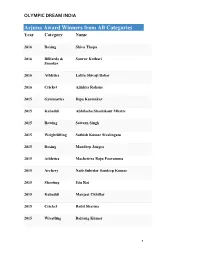
Arjuna Award Winners from All Categories Year Category Name
OLYMPIC DREAM INDIA Arjuna Award Winners from All Categories Year Category Name 2016 Boxing Shiva Thapa 2016 Billiards & Sourav Kothari Snooker 2016 Athletics Lalita Shivaji Babar 2016 Cricket Ajinkya Rahane 2015 Gymnastics Dipa Karmakar 2015 Kabaddi Abhilasha Shashikant Mhatre 2015 Rowing Sawarn Singh 2015 Weightlifting Sathish Kumar Sivalingam 2015 Boxing Mandeep Jangra 2015 Athletics Machettira Raju Poovamma 2015 Archery Naib Subedar Sandeep Kumar 2015 Shooting Jitu Rai 2015 Kabaddi Manjeet Chhillar 2015 Cricket Rohit Sharma 2015 Wrestling Bajrang Kumar 1 OLYMPIC DREAM INDIA 2015 Wrestling Babita Kumari 2015 Wushu Yumnam Sanathoi Devi 2015 Swimming Sharath M. Gayakwad (Paralympic Swimming) 2015 RollerSkating Anup Kumar Yama 2015 Badminton Kidambi Srikanth Nammalwar 2015 Hockey Parattu Raveendran Sreejesh 2014 Weightlifting Renubala Chanu 2014 Archery Abhishek Verma 2014 Athletics Tintu Luka 2014 Cricket Ravichandran Ashwin 2014 Kabaddi Mamta Pujari 2014 Shooting Heena Sidhu 2014 Rowing Saji Thomas 2014 Wrestling Sunil Kumar Rana 2014 Volleyball Tom Joseph 2014 Squash Anaka Alankamony 2014 Basketball Geetu Anna Jose 2 OLYMPIC DREAM INDIA 2014 Badminton Valiyaveetil Diju 2013 Hockey Saba Anjum 2013 Golf Gaganjeet Bhullar 2013 Athletics Ranjith Maheshwari (Athlete) 2013 Cricket Virat Kohli 2013 Archery Chekrovolu Swuro 2013 Badminton Pusarla Venkata Sindhu 2013 Billiards & Rupesh Shah Snooker 2013 Boxing Kavita Chahal 2013 Chess Abhijeet Gupta 2013 Shooting Rajkumari Rathore 2013 Squash Joshna Chinappa 2013 Wrestling Neha Rathi 2013 Wrestling Dharmender Dalal 2013 Athletics Amit Kumar Saroha 2012 Wrestling Narsingh Yadav 2012 Cricket Yuvraj Singh 3 OLYMPIC DREAM INDIA 2012 Swimming Sandeep Sejwal 2012 Billiards & Aditya S. Mehta Snooker 2012 Judo Yashpal Solanki 2012 Boxing Vikas Krishan 2012 Badminton Ashwini Ponnappa 2012 Polo Samir Suhag 2012 Badminton Parupalli Kashyap 2012 Hockey Sardar Singh 2012 Kabaddi Anup Kumar 2012 Wrestling Rajinder Kumar 2012 Wrestling Geeta Phogat 2012 Wushu M. -

The Biography of Kevin Pietersen Pdf, Epub, Ebook
KP - THE BIOGRAPHY OF KEVIN PIETERSEN PDF, EPUB, EBOOK Marcus Stead | 288 pages | 01 Oct 2013 | John Blake Publishing Ltd | 9781782194316 | English | London, United Kingdom KP - the Biography of Kevin Pietersen PDF Book Pietersen captained England in the fifth ODI against New Zealand after Paul Collingwood was banned for four games for a slow over-rate during the previous match. With the recent introduction of more entertaining players - Jos Buttler, Moeen Ali, the resurgent Joe Root, Gary Ballance Trott with several more higher gears , Ben Stokes - it might become easier to forget Pietersen quicker than he imagines. Lists with This Book. But I just sat back and laughed at the opposition, with their swearing and 'traitor' remarks In that series he made 90 not out and got 2—22 with the ball. No trivia or quizzes yet. C'mon Kevin this is an autobiography not a case study on the behaviour of Andy Flower and Matt Prior. Aug 23, John rated it did not like it. Night of the LongWinded. I am just fortunate that I am able to hit it a bit further. Showing He edged his fifth ball to Chamara Silva at slip, who flicked the ball up for wicketkeeper Kumar Sangakkara to complete the catch. He had a good partnership with Andrew Flintoff where the pair put on very quickly. Retrieved on 5 June Kevin Pietersen is without doubt one of the most gifted players of his generation. Andrew Strauss is respected but also portrayed as a deluded, fogeyish figure. To some extent, he was certainly his own worst enemy. -

The Late Dr H. B. Singh
T he Late Dr H. B. Singh (L916-1974) WILD EDIBLE PLANTS OF INDIA H. B. SINGH AND R. K. ARORA National Bureau of Plant Genetie Resources 1. A. R. 1. Campus, New Delhi . !CAB INDIAN COUNCIL OF AGRIOULTURAL RESEAROH NEW DELHI FIRST PRINTED, MARCH 1978 Chiif Editor : P. L. JAISWAL Editor,' K. B. NAIR Asstt. Editor,' I. J. LALL Clti~f Production o'{jiccr " KRlSHAN KUMAR ProdllctiDn Assistant : J. L. CULlAN! Price : Rs 8.20 A'~S\\~ ~i fa, ii, It, l.H'i.~.4.1l.~. IJ.lWDJlLBl. Printed in Indi;; by n .. D. Sen .at the N,,\J;I :h1u(lr;1.n (P) Ltd., 170~! Acharya .Prafulla Chandxa Road, Calcutta and publi,hed by P.j.:Toseph, Uncler Secretary for the Indian Council of Agricultural Rcse,!rch, New Delhi. Dr HARBHAJAN SINGH (19l6-l974) DR Harbhajan Singh was born at Pusa (Bihar) on February 6, 1916. After obtaining the degree of Master of Science in Botany fi'om Agra Uni versity in 1938, he joined the Indian (then Imperial) Agricultural Research Institute for a t-wo-year Diploma course of Associateship in Economic Botany. Thereafter, he was taken up on the research staff of the Division of Botany where h.e pursued his scientific career with imlllcnse zeal and devotion, and rose to the position of the Head of the Division of Plant Introduction in that Institute. Dr Singh was among the first to l'calisc the immense possibilities of crop improvcment in India through systematic plant introduction and exploration. He was a plant explorer of eminence with regard to cultivated plants and their wild relatives, and carried out one-man trips, as well as led teams of agricultural plant explorers to different parts of India and the neighbouring countries such as Nepal. -

Will T20 Clean Sweep Other Formats of Cricket in Future?
Munich Personal RePEc Archive Will T20 clean sweep other formats of Cricket in future? Subhani, Muhammad Imtiaz and Hasan, Syed Akif and Osman, Ms. Amber Iqra University Research Center 2012 Online at https://mpra.ub.uni-muenchen.de/45144/ MPRA Paper No. 45144, posted 16 Mar 2013 09:41 UTC Will T20 clean sweep other formats of Cricket in future? Muhammad Imtiaz Subhani Iqra University Research Centre-IURC , Iqra University- IU, Defence View, Shaheed-e-Millat Road (Ext.) Karachi-75500, Pakistan E-mail: [email protected] Tel: (92-21) 111-264-264 (Ext. 2010); Fax: (92-21) 35894806 Amber Osman Iqra University Research Centre-IURC , Iqra University- IU, Defence View, Shaheed-e-Millat Road (Ext.) Karachi-75500, Pakistan E-mail: [email protected] Tel: (92-21) 111-264-264 (Ext. 2010); Fax: (92-21) 35894806 Syed Akif Hasan Iqra University- IU, Defence View, Shaheed-e-Millat Road (Ext.) Karachi-75500, Pakistan E-mail: [email protected] Tel: (92-21) 111-264-264 (Ext. 1513); Fax: (92-21) 35894806 Bilal Hussain Iqra University Research Centre-IURC , Iqra University- IU, Defence View, Shaheed-e-Millat Road (Ext.) Karachi-75500, Pakistan Tel: (92-21) 111-264-264 (Ext. 2010); Fax: (92-21) 35894806 Abstract Enthralling experience of the newest format of cricket coupled with the possibility of making it to the prestigious Olympic spectacle, T20 cricket will be the most important cricket format in times to come. The findings of this paper confirmed that comparatively test cricket is boring to tag along as it is spread over five days and one-days could be followed but on weekends, however, T20 cricket matches, which are normally played after working hours and school time in floodlights is more attractive for a larger audience. -

Run Rule Max Per Inning, Unlimited Runs on Sixth Inning Only If Reached. ● Coach Conferences with Team: 1 Per Inning, 2Nd Will Result in Removal of Pitcher
10U Division Softball Rules Revised 2/2015 Game Length: Games will be six (6) innings in length with no new inning to start after 1 hour and 30 minutes or with safe light conditions exist as determined by the umpire. If unsafe light conditions exist, the score reverts back to the last completed inning. Rules: Playing rules will follow in order of precedent: Hemet Youth house rules, followed by PONY Softball rule book. ● Pitching distance will be set at 35’ ● An 11” softball shall be used for league play ● All players attending the game will bat. Players arriving after the start of the game will bat at the end of the line up. ● Player(s) leaving the game early due to injury or illness will receive an “out” the first time the players batting turn occurs. Any subsequent atbats for the same player will be skipped with no penalty. ● Mandatory Play Rule: No player will sit in the dugout consecutively more than one defensive inning. Penalty: Manager ejected from game. ● Leadoffs are allowed only after the ball has left the pitcher’s hand. Leaving the base prior to the ball leaving the pitcher’s hand constitutes an out. ● Ball is DEAD when hit into foul territory. ● 2 minutes between innings and 5 warm up pitches. ● When changing a pitcher in the middle of an inning, the pitcher is allowed 2 minutes for warm ups and/or 5 warm up pitches. ● Pitchers can pitch three (3) innings a game, six (6) innings in a calendar week, with mandatory 48 hours rest in between games if two (2) innings are pitched in the prior game. -

Objective Measures of Performance in the World Cup of Cricket
OBJECTIVE MEASURES OF PERFORMANCE IN THE WORLD CUP OF CRICKET. Stephen R Clarke, Swinburne University of Technology, PO Box 218, Hawthorn, 3122, Australia, +61 3 9214 8885, sclarke@swin, edu. au Paul Allsopp, Swinburne University of Technology, Hawthorn, 3122, Australia, +61 3 9307 000, paulalls@telstra, easymail, com.au ABSTRACT Since luck can play a big part in tournament success, team management should use more objective measures of performance. A Linear model is used to fit least squares ratings to margins of victory in the World Cup of cricket. The Duckworth/Lewis (D/L) rain interruption rules are applied to second innings victories to create a margin of victory in runs, equivalent to that for the team batting first. Results show that while the better teams progressed through the first round of the competition, some injustices occurred in the Super-Six round. Ordering teams by average margin of victory in runs gives similar results to the linear model, and its official publication and use as a tie breaker is suggested. INTRODUCTION The 1999 World Cup of (one-day) cricket was contested by 12 teams comprising the nine test match playing countries plus Scotland, Kenya and Bangladesh. These were 'seeded' and divided into two groups. Group A comprised Sri Lanka, India, South Africa, England, Zimbabwe and Kenya. Group B comprised Australia, West Indies, Pakistan, New Zealand, Bangladesh and Scotland. After the round robin group matches, the top three teams from Group A (South Africa, India and Zimbabwe) and Group 13 (Pakistan, Australia and New Zealand) progressed to the Super-Six, where they played each team from the other group. -

The Natwest Series 2001
The NatWest Series 2001 CONTENTS Saturday23June 2 Match review – Australia v England 6 Regulations, umpires & 2002 fixtures 3&4 Final preview – Australia v Pakistan 7 2000 NatWest Series results & One day Final act of a 5 2001 fixtures, results & averages records thrilling series AUSTRALIA and Pakistan are both in superb form as they prepare to bring the curtain down on an eventful tournament having both won their last group games. Pakistan claimed the honours in the dress rehearsal for the final with a memo- rable victory over the world champions in a dramatic day/night encounter at Trent Bridge on Tuesday. The game lived up to its billing right from the onset as Saeed Anwar and Saleem Elahi tore into the Australia attack. Elahi was in particularly impressive form, blast- ing 79 from 91 balls as Pakistan plundered 290 from their 50 overs. But, never wanting to be outdone, the Australians responded in fine style with Adam Gilchrist attacking the Pakistan bowling with equal relish. The wicketkeep- er sensationally raced to his 20th one-day international half-century in just 29 balls on his way to a quick-fire 70. Once Saqlain Mushtaq had ended his 44-ball knock however, skipper Waqar Younis stepped up to take the game by the scruff of the neck. The pace star is bowling as well as he has done in years as his side come to the end of their tour of England and his figures of six for 59 fully deserved the man of the match award and to take his side to victory. -

Brand Ambassadors
DESIZN CIRCLE Fashion GK – Module 2020 • Reebok – Katrina Kaif • Pro-Kabbadi team Patna Pirates – Neetu Chandra • V-Nourish – Shahrukh Khan • Brune & Bareskin – Harbhajan Singh • Gatorade – Hima Das • Havells male grooming products – Vicky Kaushal • Bharat-Pe – Salman Khan • MG Motor India – Benedict Cumberbatch • Indian Terrain – M.S. Dhoni • Himalaya Men – Virat Kohli & Rishab Pant • PolicyX.com – Virendra Sehwag • Lloyd – Ranveer Singh & Deepika Padukone • Puma – M.C. Mary Kom • Swasth Immunised India Campaign – Kareena Kapoor • Denver – Mahesh Babu • Mobile Premier League – Virat Kohli • Clean India Mission – PV Sindhu & Sakshi Malik • Kurkure – Taapsee Pannu • Mwoop – Sakshi Maggo • Poker Starts India – Nawazuddin SiddiQui • Kent – Shahrukh Khan • Bharat Matrimony – MS Doni • Apollo Tyres – Sachin Tendulkar • Uber Eats – Alia Bhatt • SBI – Swapna Barman • Datsun India – Amir Khan • Holosuit – Yuvraj Singh • Maruti Suzuki Arena – Varun Dhawan • DishTV – Ranveer Singh • Mastercard – MS Doni • Nokia – Alia Bhatt • Siyarams – Ranveer Singh • Rupa & Company – Anushka Sharma (Softline) • Dabur Honey – JacQueline Fernandez • Isuzu India – Jonty Rhodes • Road Safety – Akshay Kumar • Flipkart – Ranbir Kapoor & Shraddha Kapoor • Assam (Sports) – Hima Das • Philips (Male) – Virat Kohli • Indigo Paints – MS Dhoni • Dabur FEM – Kirti Sanon • Dollar Missy – Chitrangda Singh • Reebok – Nathalie Emmanuel • L’oreal – Amber Heard • Kraftz India – Sourav Ganguly • Educate Girls (Non-Profit Organisation) – Katrina Kaif • BATA India – Kirti Sanon • Whirlpool -
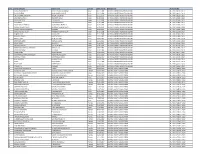
Sl. No. Name of Players Father Name Gender Date of Birth Member Unit
Sl. No. Name of Players Father Name Gender Date of Birth Member Unit PLAYER ID NO 1 VIKAS VISHNU PILLAY PILLAY VISHNU MANIKAM Male 20.11.1989 AIR INDIA SPORTS PROMOTION BOARD PL / AIR / 00042 / 2013 2 YOUSUF AFFAN MOHAMMED YOUSUF Male 29.12.1994 AIR INDIA SPORTS PROMOTION BOARD PL / AIR / 00081 / 2013 3 LALIT KUMAR UPADHYAY SATISH UPADHYAY Male 01.12.1993 AIR INDIA SPORTS PROMOTION BOARD PL / AIR / 00090 / 2013 4 SHIVENDRA SINGH JHAMMAN SINGH Male 09.06.1983 AIR INDIA SPORTS PROMOTION BOARD PL / AIR / 01984 / 2014 5 ARJUN HALAPPA B K HALAPPA Male 17.12.1980 AIR INDIA SPORTS PROMOTION BOARD PL / AIR / 01985 / 2014 6 JOGA SINGH HARJINDER SINGH Male 01.01.1986 AIR INDIA SPORTS PROMOTION BOARD PL / AIR / 01986 / 2014 7 GIRISH RAVAJI PIMPALE RAVAJI BHIKU PIMPALE Male 06.05.1983 AIR INDIA SPORTS PROMOTION BOARD PL / AIR / 01987 / 2014 8 VIKRAM VISHNU PILLAY MANIKAM VISHNU PILLAY Male 27.11.1981 AIR INDIA SPORTS PROMOTION BOARD PL / AIR / 01988 / 2014 9 VINAYA VAKKALIGA SWAMY B SWAMY Male 24.11.1985 AIR INDIA SPORTS PROMOTION BOARD PL / AIR / 01989 / 2014 10 VINOD VISHNU PILLAY MANIKAM VISHNU PILLAY Male 05.12.1988 AIR INDIA SPORTS PROMOTION BOARD PL / AIR / 01990 / 2014 11 SAMEER DAD KHUDA DAD Male 25.11.1978 AIR INDIA SPORTS PROMOTION BOARD PL / AIR / 01991 / 2014 12 PRABODH TIRKEY WALTER TIREKY Male 15.12.1985 AIR INDIA SPORTS PROMOTION BOARD PL / AIR / 01992 / 2014 13 BIMAL LAKRA MARCUS LAKRA Male 04.05.1980 AIR INDIA SPORTS PROMOTION BOARD PL / AIR / 01993 / 2014 14 BIRENDAR LAKRA MARCUS LAKRA Male 22.12.1985 AIR INDIA SPORTS PROMOTION BOARD