Goals Rotational Quantities As Vectors Angular Momentum Q Math: Cross
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Rotational Motion (The Dynamics of a Rigid Body)
University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln Robert Katz Publications Research Papers in Physics and Astronomy 1-1958 Physics, Chapter 11: Rotational Motion (The Dynamics of a Rigid Body) Henry Semat City College of New York Robert Katz University of Nebraska-Lincoln, [email protected] Follow this and additional works at: https://digitalcommons.unl.edu/physicskatz Part of the Physics Commons Semat, Henry and Katz, Robert, "Physics, Chapter 11: Rotational Motion (The Dynamics of a Rigid Body)" (1958). Robert Katz Publications. 141. https://digitalcommons.unl.edu/physicskatz/141 This Article is brought to you for free and open access by the Research Papers in Physics and Astronomy at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in Robert Katz Publications by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. 11 Rotational Motion (The Dynamics of a Rigid Body) 11-1 Motion about a Fixed Axis The motion of the flywheel of an engine and of a pulley on its axle are examples of an important type of motion of a rigid body, that of the motion of rotation about a fixed axis. Consider the motion of a uniform disk rotat ing about a fixed axis passing through its center of gravity C perpendicular to the face of the disk, as shown in Figure 11-1. The motion of this disk may be de scribed in terms of the motions of each of its individual particles, but a better way to describe the motion is in terms of the angle through which the disk rotates. -

Position, Displacement, Velocity Big Picture
Position, Displacement, Velocity Big Picture I Want to know how/why things move I Need a way to describe motion mathematically: \Kinematics" I Tools of kinematics: calculus (rates) and vectors (directions) I Chapters 2, 4 are all about kinematics I First 1D, then 2D/3D I Main ideas: position, velocity, acceleration Language is crucial Physics uses ordinary words but assigns specific technical meanings! WORD ORDINARY USE PHYSICS USE position where something is where something is velocity speed speed and direction speed speed magnitude of velocity vec- tor displacement being moved difference in position \as the crow flies” from one instant to another Language, continued WORD ORDINARY USE PHYSICS USE total distance displacement or path length traveled path length trav- eled average velocity | displacement divided by time interval average speed total distance di- total distance divided by vided by time inter- time interval val How about some examples? Finer points I \instantaneous" velocity v(t) changes from instant to instant I graphically, it's a point on a v(t) curve or the slope of an x(t) curve I average velocity ~vavg is not a function of time I it's defined for an interval between instants (t1 ! t2, ti ! tf , t0 ! t, etc.) I graphically, it's the \rise over run" between two points on an x(t) curve I in 1D, vx can be called v I it's a component that is positive or negative I vectors don't have signs but their components do What you need to be able to do I Given starting/ending position, time, speed for one or more trip legs, calculate average -

Physics B Topics Overview ∑
Physics 106 Lecture 1 Introduction to Rotation SJ 7th Ed.: Chap. 10.1 to 3 • Course Introduction • Course Rules & Assignment • TiTopics Overv iew • Rotation (rigid body) versus translation (point particle) • Rotation concepts and variables • Rotational kinematic quantities Angular position and displacement Angular velocity & acceleration • Rotation kinematics formulas for constant angular acceleration • Analogy with linear kinematics 1 Physics B Topics Overview PHYSICS A motion of point bodies COVERED: kinematics - translation dynamics ∑Fext = ma conservation laws: energy & momentum motion of “Rigid Bodies” (extended, finite size) PHYSICS B rotation + translation, more complex motions possible COVERS: rigid bodies: fixed size & shape, orientation matters kinematics of rotation dynamics ∑Fext = macm and ∑ Τext = Iα rotational modifications to energy conservation conservation laws: energy & angular momentum TOPICS: 3 weeks: rotation: ▪ angular versions of kinematics & second law ▪ angular momentum ▪ equilibrium 2 weeks: gravitation, oscillations, fluids 1 Angular variables: language for describing rotation Measure angles in radians simple rotation formulas Definition: 360o 180o • 2π radians = full circle 1 radian = = = 57.3o • 1 radian = angle that cuts off arc length s = radius r 2π π s arc length ≡ s = r θ (in radians) θ ≡ rad r r s θ’ θ Example: r = 10 cm, θ = 100 radians Æ s = 1000 cm = 10 m. Rigid body rotation: angular displacement and arc length Angular displacement is the angle an object (rigid body) rotates through during some time interval..... ...also the angle that a reference line fixed in a body sweeps out A rigid body rotates about some rotation axis – a line located somewhere in or near it, pointing in some y direction in space • One polar coordinate θ specifies position of the whole body about this rotation axis. -

Oscillations
CHAPTER FOURTEEN OSCILLATIONS 14.1 INTRODUCTION In our daily life we come across various kinds of motions. You have already learnt about some of them, e.g., rectilinear 14.1 Introduction motion and motion of a projectile. Both these motions are 14.2 Periodic and oscillatory non-repetitive. We have also learnt about uniform circular motions motion and orbital motion of planets in the solar system. In 14.3 Simple harmonic motion these cases, the motion is repeated after a certain interval of 14.4 Simple harmonic motion time, that is, it is periodic. In your childhood, you must have and uniform circular enjoyed rocking in a cradle or swinging on a swing. Both motion these motions are repetitive in nature but different from the 14.5 Velocity and acceleration periodic motion of a planet. Here, the object moves to and fro in simple harmonic motion about a mean position. The pendulum of a wall clock executes 14.6 Force law for simple a similar motion. Examples of such periodic to and fro harmonic motion motion abound: a boat tossing up and down in a river, the 14.7 Energy in simple harmonic piston in a steam engine going back and forth, etc. Such a motion motion is termed as oscillatory motion. In this chapter we 14.8 Some systems executing study this motion. simple harmonic motion The study of oscillatory motion is basic to physics; its 14.9 Damped simple harmonic motion concepts are required for the understanding of many physical 14.10 Forced oscillations and phenomena. In musical instruments, like the sitar, the guitar resonance or the violin, we come across vibrating strings that produce pleasing sounds. -
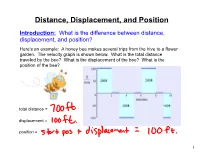
Distance, Displacement, and Position
Distance, Displacement, and Position Introduction: What is the difference between distance, displacement, and position? Here's an example: A honey bee makes several trips from the hive to a flower garden. The velocity graph is shown below. What is the total distance traveled by the bee? What is the displacement of the bee? What is the position of the bee? total distance = displacement = position = 1 Warm-up A particle moves along the x-axis so that the acceleration at any time t is given by: At time , the velocity of the particle is and at time , the position is . (a) Write an expression for the velocity of the particle at any time . (b) For what values of is the particle at rest? (c) Write an expression for the position of the particle at any time . (d) Find the total distance traveled by the particle from to . 2 Warm-up Answers (a) (b) (c) (d) Total Distance = 3 Now, using the equation from the warm-up find the following (WITHOUT A CALCULATOR): (a) the total distance from 0 to 4 (b) the displacement from 0 to 4 4 To find the displacement (position shift) from the velocity function, we just integrate the function. The negative areas below the x-axis subtract from the total displacement. Displacement = To find the distance traveled we have to use absolute value. Distance traveled = To find the distance traveled by hand you must: Find the roots of the velocity equation and integrate in pieces, just like when we found the area between a curve and x-axis. -

Force-Based Element Vs. Displacement-Based Element
Force-based Element vs. Displacement-based Element Vesna Terzic UC Berkeley December 2011 Agenda • Introduction • Theory of force-based element (FBE) • Theory of displacement-based element (DBE) • Examples • Summary and conclusions • Q & A with web participants Introduction • Contrary to concentrated plasticity models (elastic element with rotational springs at element ends) force-based element (FBE) and displacement- based element (DBE) permit spread of plasticity along the element (distributed plasticity models). • Distributed plasticity models allow yielding to occur at any location along the element, which is especially important in the presence of distributed element loads (girders with high gravity loads). Introduction • OpenSees commands for defining FBE and DBE have the same arguments: element forceBeamColumn $eleTag $iNode $jNode $numIntgrPts $secTag $transfTag element displacementBeamColumn $eleTag $iNode $jNode $numIntgrPts $secTag $transfTag • However a beam-column element needs to be modeled differently using these two elements to achieve a comparable level of accuracy. • The intent of this seminar is to show users how to properly model frame elements with both FBE and DBE. • In order to enhance your understanding of these two elements and to assure their correct application I will present the theory of these two elements and demonstrate their application on two examples. Transformation of global to basic system Element u p u p p aT q v = af u GeometricTran = f q3,v3 q1,v1 v q Basic System q2,v 2 Displacement-based element • The displacement-based approach follows standard finite element procedures where we interpolate section deformations from an approximate displacement field then use the PVD to form the element equilibrium relationship. -

Angular Kinematics Contents of the Lesson
Angular Kinematics Contents of the Lesson Angular Motion and Kinematics Angular Distance and Angular Displacement. Angular Speed and Angular Velocity Angular Acceleration Questions. Motion “change in the position of an object with respect to some reference frame.” Planes and Axis. Angular Motion “Rotation of a object around a central imaginary line” Characteristics: ◦ Axis of rotation. ◦ Whole object moves. Identify the angular motion Angular motion in the human body “most of movement are angular” In the human body; ◦ Joint= Axis of rotation. ◦ Body segment= object or rotatory body. ◦ Initial position= anatomical position. Kinematics; Angular Kinematics “Description of Angular Motion” Seeks to answer? “How much something has rotated?” “How fast something is rotating?” etc. Units of measurements Degrees. Radian Units of measurement Revolutions 1 revolution= 1 circle= 360 degrees= 2휋.radians Angular Distance “Sum of all angular changes undergone by a rotatory body” Unit: degrees, radian revolution. Angular Displacement “difference between the initial and final position of a rotatory body around an axis of rotation with regards to direction.” Direction= counter clockwise or clockwise In Human movement= Flexion,Extension,etc. What will be the angular displacement? Angular Speed “Scalar quantity” “angular distance covered divided by time interval over which the motion occurred” Angular Velocity “Vector quantity” “rate of change of angular position or angular displacement w.r.t time” Angular speed and Velocity Angular speed = degree/sec, rad/sec, or revolution/sec. Angular Velocity= degree/sec, rad/sec, or revolution/sec counterclockwise, clockwise or flexion or extension, etc. Angular Acceleration “Rate of change of angular velocity w.r.t time.” Unit= degree/sec² Calculate acceleration. -

Analysis on Torque, Flowrate, and Volumetric Displacement of Gerotor Pump/Motor
연구논문 Journal of Drive and Control, Vol.17 No.2 pp.28-37 Jun. 2020 ISSN 2671-7972(print) ISSN 2671-7980(online) http://dx.doi.org/10.7839/ksfc.2020.17.2.028 Analysis on Torque, Flowrate, and Volumetric Displacement of Gerotor Pump/Motor Hongsik Yun1, Young-Bog Ham2 and Sungdong Kim1* Received: 02 Apr. 2020, Revised: 14 May 2020, Accepted: 18 May 2020 Key Words:Torque Equilibrium, Energy Conservation, Volumetric Displacement, Flowrate, Rotation Speed, Gerotor Pump/Motor Abstract: It is difficult to analytically derive the relationship among volumetric displacement, flowrate, torque, and rotation speed regarding an instantaneous position of gerotor hydraulic pumps/motors. This can be explained by the geometric shape of the rotors, which is highly complicated. Herein, an analytical method for the instantaneous torque, rotation speed, flowrate, and volumetric displacement of a pump/motor is proposed. The method is based on two physical concepts: energy conservation and torque equilibrium. The instantaneous torque of a pump/motor shaft is determined for the posture of rotors from the torque equilibrium. If the torque equilibrium is combined with the energy conservation between the hydraulic energy of the pump/motor and the mechanical input/output energy, the formula for determining the instantaneous volumetric displacement and flowrate is derived. The numerical values of the instantaneous volumetric displacement, torque, rotation speed, and flowrate are calculated via the MATLAB software programs, and they are illustrated for the case in which inner and outer rotors rotate with respect to fixed axes. The degrees of torque fluctuation, speed fluctuation, and flowrate fluctuation can be observed from their instantaneous values. -

Hydraulophone Design Considerations: Absement, Displacement, and Velocity-Sensitive Music Keyboard in Which Each Key Is a Water Jet
Hydraulophone Design Considerations: Absement, Displacement, and Velocity-Sensitive Music Keyboard in which each key is a Water Jet Steve Mann, Ryan Janzen, Mark Post University of Toronto, Dept. of Electrical and Computer Engineering, Toronto, Ontario, Canada For more information, see http://funtain.ca ABSTRACT General Terms We present a musical keyboard that is not only velocity- Measurement, Performance, Design, Experimentation, Hu- sensitive, but in fact responds to absement (presement), dis- man Factors, Theory placement (placement), velocity, acceleration, jerk, jounce, etc. (i.e. to all the derivatives, as well as the integral, of Keywords displacement). Fluid-user-interface, tangible user interface, direct user in- Moreover, unlike a piano keyboard in which the keys reach terface, water-based immersive multimedia, FUNtain, hy- a point of maximal displacement, our keys are essentially draulophone, pneumatophone, underwater musical instru- infinite in length, and thus never reach an end to their key ment, harmelodica, harmelotron (harmellotron), duringtouch, travel. Our infinite length keys are achieved by using water haptic surface, hydraulic-action, tracker-action jet streams that continue to flow past the fingers of a per- son playing the instrument. The instrument takes the form 1. INTRODUCTION: VELOCITY SENSING of a pipe with a row of holes, in which water flows out of KEYBOARDS each hole, while a user is invited to play the instrument by High quality music keyboards are typically velocity-sensing, interfering with the flow of water coming out of the holes. i.e. the notes sound louder when the keys are hit faster. The instrument resembles a large flute, but, unlike a flute, Velocity-sensing is ideal for instruments like the piano, there is no complicated fingering pattern. -

Force Transmissibility Versus Displacement Transmissibility
Journal of Sound and Vibration ] (]]]]) ]]]–]]] Contents lists available at ScienceDirect Journal of Sound and Vibration journal homepage: www.elsevier.com/locate/jsvi Force transmissibility versus displacement transmissibility Y.E. Lage a, M.M. Neves a,n, N.M.M. Maia a, D. Tcherniak b a LAETA, IDMEC, Instituto Superior Técnico, Universidade de Lisboa, Av. Rovisco Pais 1, 1049-001 Lisboa, Portugal b Brüel & Kjaer Sound and Vibration Measurement A/S, Skodsborgvej 307, DK 2850 Naerum, Denmark article info abstract Article history: It is well-known that when a single-degree-of-freedom (sdof) system is excited by a Received 5 June 2013 continuous motion of the foundation, the force transmissibility, relating the force transmitted Received in revised form to the foundation to the applied force, equals the displacement transmissibility. Recent 18 May 2014 developments in the generalization of the transmissibility to multiple-degree-of-freedom Accepted 19 May 2014 (mdof) systems have shown that similar simple and direct relations between both types of Handling Editor: H. Ouyang transmissibility do not appear naturally from the definitions, as happens in the sdof case. In this paper, the authors present their studies on the conditions under which it is possible to establish a relation between force transmissibility and displacement transmissibility for mdof systems. As far as the authors are aware, such a relation is not currently found in the literature, which is justified by being based on recent developments in the transmissibility concept for mdof systems. Indeed, it does not appear naturally, but the authors observed that the needed link is present when the displacement transmissibility is obtained between the same coordinates where the applied and reaction forces are considered in the force transmissibility case; this implies that the boundary conditions are not exactly the same and instead follow some rules. -

Chapter 24 Physical Pendulum
Chapter 24 Physical Pendulum 24.1 Introduction ........................................................................................................... 1 24.1.1 Simple Pendulum: Torque Approach .......................................................... 1 24.2 Physical Pendulum ................................................................................................ 2 24.3 Worked Examples ................................................................................................. 4 Example 24.1 Oscillating Rod .................................................................................. 4 Example 24.3 Torsional Oscillator .......................................................................... 7 Example 24.4 Compound Physical Pendulum ........................................................ 9 Appendix 24A Higher-Order Corrections to the Period for Larger Amplitudes of a Simple Pendulum ..................................................................................................... 12 Chapter 24 Physical Pendulum …. I had along with me….the Descriptions, with some Drawings of the principal Parts of the Pendulum-Clock which I had made, and as also of them of my then intended Timekeeper for the Longitude at Sea.1 John Harrison 24.1 Introduction We have already used Newton’s Second Law or Conservation of Energy to analyze systems like the spring-object system that oscillate. We shall now use torque and the rotational equation of motion to study oscillating systems like pendulums and torsional springs. 24.1.1 Simple -

Rotation: Kinematics
Rotation: Kinematics Rotation refers to the turning of an object about a fixed axis and is very commonly encountered in day to day life. The motion of a fan, the turning of a door knob and the opening of a bottle cap are a few examples of rotation. Rotation is also commonly observed as a component of more complex motions that result as a combination of both rotation and translation. The motion of a wheel of a moving bicycle, the motion of a blade of a moving helicopter and the motion of a curveball are a few examples of combined rotation and translation. This module focuses on the kinematics of pure rotation. This module begins by defining the angular variables and then proceeds to describe the relation between these variables and the variables of linear motion. Angular Variables Angular Position Consider an object rotating about a fixed axis. Let us define a coordinate system such that the axis of rotation passes through the origin and is perpendicular to the x- and y- axes. Fig. 1 shows a view of the x-y plane. If a reference line is drawn through the origin and a fixed point in the object, the angle between this line and a fixed direction is used to define the angular position of the object. In Fig. 1, the angular position is measured from the positive x-direction. Fig. 1: Rotating object - Angular position. Also, from geometry, the angular position can be written as the ratio of the length of the path traveled by any point on the reference line measured from the fixed direction to the radius of the path, ...Eq.