DOCSLIB.ORG

Any Molecule Is Said to Have N-Fold Axis of Symmetry, Cn, If the Rotation

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Any Molecule Is Said to Have N-Fold Axis of Symmetry, Cn, If the Rotation Glossary A Axis of Symmetry: Any molecule is said to have n-fold axis of symmetry, Cn, if the rotation of the molecule about that axis by 3600/n produces an orientation which is indistinguishable from the initial one. The general symbol of the proper axis of rotation is Cn where the subscript n denotes the order of axis I Improper Axes of Symmetry: If the rotation of a molecule about an axis through an axis by 3600/n followed by reflection through a plane perpendicular to the axis produces an orientation which is indistinguishable from the initial one ,it is called improper rotation symmetry and the axis is called n-fold axis of improper rotation(Sn). Inversion Operation: If the reflection of all the atoms of a molecule through a point within the molecule produces an orientation which is indistinguishable from the initial one, it is called inversion operation and that point is called centre of symmetry. M Metal Carbonyl: Metal carbonyls are coordination complexes of transition metals with carbon monoxide ligands. Metal carbonyls are useful in organic synthesis and as catalysts or catalyst precursors in homogeneous catalysis, such as hydroformylation and Reppe chemistry. In the Mond process, nickel carbonyl is used to produce pure nickel. In organometallic chemistry, metal carbonyls serve as precursors for the preparation of other organometalic complexes P Plane of Symmetry: Reflection symmetry, line symmetry, mirror symmetry, mirror-image symmetry, or bilateral symmetry is symmetry with respect to reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry. The plane of symmetry may be regarded as the hypothetical plane passing through a molecule which bisects the molecule into two equal halves which are just mirror-images of each other. The standard symbol for the plane of symmetry is σ. The same symbol is also used for the reflection operation. There are three types of plane of symmetry: i) Vertical plane of symmetry (σv): The plane of symmetry which is parallel to the principal axis or which contains the principal axis is called vertical plane of symmetry. ii) Horizontal plane of symmetry (σh): The plane of symmetry which is perpendicular to the principal axis of symmetry is called horizontal plane of symmetry. iii) Dihedral plane of symmetry (σd): The plane of symmetry which bisects the angle between two C2 axes of symmetry is called the dihedral plane of symmetry. S Symmetry Operation: In the context of molecular symmetry, a symmetry operation is a permutation of atoms such that the molecule or crystal is transformed into a state indistinguishable from the starting state. Two basic facts follow from this definition, which emphasize its usefulness. 1. Physical properties must be invariant with respect to symmetry operations. 2. Symmetry operations can be collected together in groups which are isomorphous to permutation groups. SymmetryElement: A symmetry element is a point of reference about which symmetry operations can take place. In particular, symmetry elements can be centers of inversion, axes of rotation and mirror planes. Do You Know? Beautiful Examples of Symmetry In Nature: Sun-Moon Symmetry: while the sun’s width is about four hundred times larger than that of the moon, the sun is also about four hundred times further away. The symmetry in this ratio makes the sun and the moon appear almost the same size when seen from Earth, and therefore makes it possible for the moon to block the sun when the two are aligned Milky Way Glaxy: Having recently discovered a new section on the edges of the Milky Way Galaxy, astronomers now believe that the galaxy is a near-perfect mirror image of itself. Based on this new information, scientists are more confident in their theory that the galaxy has only two major arms: the Perseus and the Scutum- Centaurus. In addition to having mirror symmetry, the Milky Way has another incredible design—similar to nautilus shells and sunflowers—whereby each “arm” of the galaxy represents a logarithmic spiral beginning at the center of the galaxy and expanding outwards Spider Webs: There are around 5,000 types of orb web spiders, and all create nearly perfect circular webs with almost equidistant radial supports coming out of the middle and a spiral woven to catch prey. Animals: Most animals have bilateral symmetry—which means that they can be split into two matching halves, if they are evenly divided down a center line. Even humans possess bilateral symmetry, and some scientists believe that a person’s symmetry is the most important factor in whether we find them physically beautiful or not. In other words, if you have a lopsided face, you’d better hope you have a lot of other redeeming qualities Sunflowers Sunflowers boast radial symmetry and an interesting type of numerical symmetry known as the Fibonacci sequence. The Fibonacci sequence is 1, 2, 3, 5, 8, 13, 21, 24, 55, 89, 144, and so on (each number is determined by adding the two preceding numbers together). If we took the time to count the number of seed spirals in a sunflower, we’d find that the amount of spirals adds up to a Fibonacci number. In fact, a great many plants (including romanesco broccoli) produce petals, leaves, and seeds in the Fibonacci sequence,which is why it’s so hard to find a four-leaf clover. Time line: Year Description Image 1929 Hans Bethe used characters of point group operations in his study of ligand field theory in 1929, 1933 Eugene Wigner used group theory to explain the selection rules of atomic spectroscopy. 1934 Robert Mulliken was the first to publish character tables in English (1933), and E. Bright Wilson used them in 1934 to predict the symmetry of vibrational normal modes Weblinks : 1. https://www.staff.ncl.ac.uk/j.p.goss/symmetry/Molecules_pov.html 2. www.mathsisfun.com/geometry/symmetry-artist.html 3. www.ics.uci.edu/~eppstein/junkyard/sym.html 4. www.wileyindia.com 5. pubs.acs.org/doi/abs/10.1021/ic50015a049 Suggestive Reading: Elschenbroich, C. (2006). Organometallics. Weinheim: Wiley-VCH. ISBN 3-527-29390-6. Symmetry And Group Theory For Chemist (English) 01 Edition A Simple Approach to Group Theory in Chemistry by swarnalakshmi, T Saroja, R M Ezhilarasi Chemical Applications of Group Theory : F. Albert Cotton .
Load more

Recommended publications
  • Reflection Invariant and Symmetry Detection
    1 Reflection Invariant and Symmetry Detection Erbo Li and Hua Li Abstract—Symmetry detection and discrimination are of fundamental meaning in science, technology, and engineering. This paper introduces reflection invariants and defines the directional moments(DMs) to detect symmetry for shape analysis and object recognition. And it demonstrates that detection of reflection symmetry can be done in a simple way by solving a trigonometric system derived from the DMs, and discrimination of reflection symmetry can be achieved by application of the reflection invariants in 2D and 3D. Rotation symmetry can also be determined based on that. Also, if none of reflection invariants is equal to zero, then there is no symmetry. And the experiments in 2D and 3D show that all the reflection lines or planes can be deterministically found using DMs up to order six. This result can be used to simplify the efforts of symmetry detection in research areas,such as protein structure, model retrieval, reverse engineering, and machine vision etc. Index Terms—symmetry detection, shape analysis, object recognition, directional moment, moment invariant, isometry, congruent, reflection, chirality, rotation F 1 INTRODUCTION Kazhdan et al. [1] developed a continuous measure and dis- The essence of geometric symmetry is self-evident, which cussed the properties of the reflective symmetry descriptor, can be found everywhere in nature and social lives, as which was expanded to 3D by [2] and was augmented in shown in Figure 1. It is true that we are living in a spatial distribution of the objects asymmetry by [3] . For symmetric world. Pursuing the explanation of symmetry symmetry discrimination [4] defined a symmetry distance will provide better understanding to the surrounding world of shapes.
    [Show full text]
  • Symmetry and Beauty in the Living World I Thank the Governing Body and the Director of the G.B
    SYMMETRY AND BEAUTY IN THE LIVING WORLD I thank the Governing Body and the Director of the G.B. Pant Institute of Himalayan Environment & Development for providing me this opportunity to deliver the 17th Govind Ballabh Pant Memorial Lecture. Pt. Pant, as I have understood, was amongst those who contributed in multiple ways to shape and nurture the nation in general and the Himalayan area in particular. Established to honour this great ‘Son of the Mountains’, the Institute carries enormous responsibilities and expectations from millions of people across the region and outside. Undoubtedly the multidisciplinary skills and interdisciplinary approach of the Institute and the zeal of its members to work in remote areas and harsh Himalayan conditions will succeed in achieving the long term vision of Pt. Pant for the overall development of the region. My talk ‘Symmetry and Beauty in the Living World’ attempts to discuss aspects of symmetry and beauty in nature and their evolutionary explanations. I shall explain how these elements have helped developmental and evolutionary biologists to frame and answer research questions. INTRODUCTION Symmetry is an objective feature of the living world and also of some non-living entities. It forms an essential element of the laws of nature; it is often sought by human beings when they create artefacts. Beauty has to do with a subjective assessment of the extent to which something or someone has a pleasing appearance. It is something that people aspire to, whether in ideas, creations or people. Evolutionary biology tells us that it is useful to look for an evolutionary explanation of anything to do with life.
    [Show full text]
  • Radial Symmetry Or Bilateral Symmetry Or "Spherical Symmetry"
    Symmetry in biology is the balanced distribution of duplicate body parts or shapes. The body plans of most multicellular organisms exhibit some form of symmetry, either radial symmetry or bilateral symmetry or "spherical symmetry". A small minority exhibit no symmetry (are asymmetric). In nature and biology, symmetry is approximate. For example, plant leaves, while considered symmetric, will rarely match up exactly when folded in half. Radial symmetry These organisms resemble a pie where several cutting planes produce roughly identical pieces. An organism with radial symmetry exhibits no left or right sides. They have a top and a bottom (dorsal and ventral surface) only. Animals Symmetry is important in the taxonomy of animals; animals with bilateral symmetry are classified in the taxon Bilateria, which is generally accepted to be a clade of the kingdom Animalia. Bilateral symmetry means capable of being split into two equal parts so that one part is a mirror image of the other. The line of symmetry lies dorso-ventrally and anterior-posteriorly. Most radially symmetric animals are symmetrical about an axis extending from the center of the oral surface, which contains the mouth, to the center of the opposite, or aboral, end. This type of symmetry is especially suitable for sessile animals such as the sea anemone, floating animals such as jellyfish, and slow moving organisms such as sea stars (see special forms of radial symmetry). Animals in the phyla cnidaria and echinodermata exhibit radial symmetry (although many sea anemones and some corals exhibit bilateral symmetry defined by a single structure, the siphonoglyph) (see Willmer, 1990).
    [Show full text]
  • In Square Units)
    INVESTIGATIONS and EXPLORATIONS 1.1.1 – 1.1.5 By asking questions such as “What happens if…?” and “What if I change this…?” and answering them by trying different things, we can find out quite a lot of information about different shapes. In the first five sections of this first chapter, we explore symmetry, making predictions, perimeter, area, logical arguments, and angles by investigating each of them with interesting problems. These five sections are introductory and help the teacher determine students’ prior knowledge and preview some of the ideas that will be studied in this course. The following examples illustrate the geometry ideas in this section as well as some of the algebra review topics. See the Math Notes Boxes on pages 5, 10, 15, 19, and 24. Example 1 Suppose the rug in Figure 1 is enlarged as shown. one unit one square unit Figure 1 Figure 2 Figure 3 Fill in the table below to show how the perimeter and the area of the rug change as it is enlarged. Figure Number 1 2 3 4 5 20 Perimeter (in units) Area (in square units) The perimeter of a figure is the distance (length) around the outside of the figure while the area measures the surface within the figure. The area is measured in square units while the perimeter is simply a unit of length, such as inches or centimeters. Counting the units around the outside of Figure 1, we get a perimeter of 16 units. By counting the number of square units within Figure 1, we find the area is 12 square units.
    [Show full text]
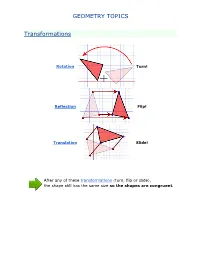
  • Geometry Topics
    GEOMETRY TOPICS Transformations Rotation Turn! Reflection Flip! Translation Slide! After any of these transformations (turn, flip or slide), the shape still has the same size so the shapes are congruent. Rotations Rotation means turning around a center. The distance from the center to any point on the shape stays the same. The rotation has the same size as the original shape. Here a triangle is rotated around the point marked with a "+" Translations In Geometry, "Translation" simply means Moving. The translation has the same size of the original shape. To Translate a shape: Every point of the shape must move: the same distance in the same direction. Reflections A reflection is a flip over a line. In a Reflection every point is the same distance from a central line. The reflection has the same size as the original image. The central line is called the Mirror Line ... Mirror Lines can be in any direction. Reflection Symmetry Reflection Symmetry (sometimes called Line Symmetry or Mirror Symmetry) is easy to see, because one half is the reflection of the other half. Here my dog "Flame" has her face made perfectly symmetrical with a bit of photo magic. The white line down the center is the Line of Symmetry (also called the "Mirror Line") The reflection in this lake also has symmetry, but in this case: -The Line of Symmetry runs left-to-right (horizontally) -It is not perfect symmetry, because of the lake surface. Line of Symmetry The Line of Symmetry (also called the Mirror Line) can be in any direction. But there are four common directions, and they are named for the line they make on the standard XY graph.
    [Show full text]
  • Symmetry Operations and Symmetry Oparators
    Dr. Lokesh Chandra Pati Dept. of Chemistry, J. K. College, Purulia Symmetry Operations and Symmetry Oparators: On order to study the symmetry of a molecule, certain operations such as rotation and reflection are performed and if by so doing, an arrangement is obtained which is indistinguishable from (superposable on) the original one, the operations is called a symmetry operation and the molecule is said to possess an element of symmetry defined by the operation performed. The symmetry operations are the ways of interchanging parts of a molecule. The symmetry operation and symmetry element are thus inseparably linked and often represented by the same symbols. Symmetry based solely on simple rotation is called symmetry of the first kind whereas symmetry on reflection or rotation- reflection is known as symmetry of second kind. Four fundamental elements of symmetry are present in the organic molecules. They are (i) Rotational axis of symmetry (Cn) (ii) Plane of symmetry (v) (iii) Centre of symmetry (i) (iv) Alternating of symmetry (Sn). Different manipulations of elements of symmetry that transform molecules into indistinguishable and identical structures are called symmetry operations and operation of identity respectively. The element of identity is designated as E or I. (i) Rotational axis of symmetry or proper axis of symmetry (Cn, where C stands for circulate and n is the fold):- If a molecule is rotated around an appropriate imaginary axis by an angle of 360/n and arrives at an arrangement indistinguishable from the original, the axis is called an n-fold simple or proper axis of symmetry or a rotational axis of symmetry of order n.
    [Show full text]
  • 39 Symmetry of Plane Figures
    39 Symmetry of Plane Figures In this section, we are interested in the symmetric properties of plane figures. By a symmetry of a plane figure we mean a motion of the plane that moves the figure so that it falls back on itself. The two types of symmetry that we discuss are Reflection Symmetry: A plane figure is symmetric about a line if it is its own image when flipped across the line. We call the reflection line the line of symmetry. In other words, a figure has a line symmetry if it can be folded along the line so that one half of the figure matches the other half. Reflection symmetry is also known as mirror symmetry, since the line of symmetry acts like a double-sided mirror. Points on each side are reflected to the opposite side. Many plane figures have several line symmetries. Figure 39.1 shows some of the plane figures with their line symmetries shown dashed. Figure 39.1 Remark 39.1 Using reflection symmetry we can establish properties for some plane figures. For example, since an isosceles triangle has one line of symmetry then the 1 base angles, i.e. angles opposed the congruent sides, are congruent. A similar property holds for isosceles trapezoids. Rotational Symmetry: A plane figure has rotational symmetry if and only if it can be rotated more than 0◦ and less than or equal to 360◦ about a fixed point called the center of rotation so that its image coincides with its original position. Figure 39.2 shows the four different rotations of a square.
    [Show full text]
  • Lesson 18 Reflection Symmetry 2017-18
    Classwork 18 NEW MATERIAL Symmetry. Symmetry is when one shape becomes exactly like another if you flip, slide or turn it. Symmetry: Reflection Reflection Symmetry (sometimes called Line Symmetry or Mirror Symmetry) is easy to spot, because one half of the shape is the reflection of the other half. The Line of Symmetry (also called the Mirror Line) can be oriented in any direction. Shapes may have several lines of symmetry, one line of symmetry or none. For example, a Triangle can have 3, or 1 or no lines of symmetry: Lesson 18 Reflection Symmetry 2017-18 1. a) Is the line drawn a symmetry line for each figure? You can cut out the images and fold them along the dashed line to check. a) b) c) d) e) f) g) h) i) 2. Some shapes you can fold in two different ways so that the sides meet. The cross-shapes below have two different symmetry lines: 2 Lesson 18 Reflection Symmetry 2017-18 Draw as many different symmetry lines as you can into these shapes. 3. REVIEW 4. 12 + 12 + 12 = 12 × x 15 + 15 = 15 × y 21 + 21 + 21 + 21 = 21 × q x = ______ y = _______ q = ______ Metric Units of Volume: A milliliter (that is "milli" and "liter" put together) is a very small amount of liquid, like a drop of water. 1000 milliliters makes up 1 liter: 1 liter = 1,000 milliliters. 3 Lesson 18 Reflection Symmetry 2017-18 a) Chris has 1 liter of water in a jug. On the way to a table he spilled some.
    [Show full text]
  • The Cytoskeleton Regulates Symmetry Transitions in Moving Amoeboid Cells Peter J
    © 2018. Published by The Company of Biologists Ltd | Journal of Cell Science (2018) 131, jcs208892. doi:10.1242/jcs.208892 RESEARCH ARTICLE The cytoskeleton regulates symmetry transitions in moving amoeboid cells Peter J. M. van Haastert*, Ineke Keizer-Gunnink and Arjan Kortholt ABSTRACT Starvation of Dictyostelium cells induces a developmental program Symmetry and symmetry breaking are essential in biology. Symmetry that is accompanied by major changes in cell shape. During the first comes in different forms: rotational symmetry, mirror symmetry three hours of starvation cells are relatively round, extend protrusions and alternating right–left symmetry (for example, gliding reflection in many directions and are unpolarized. After five hours of starvation, symmetry). Especially the transitions between the different symmetry cells become elongated and polarized, because they frequently extend forms are important because they specify crucial points in cell biology, protrusions only at the front of the cell. These polarized cells exhibit a including gastrulation in development, formation of the cleavage correlated random walk with persistence of cell movement, which furrow in cell division, or the front in cell polarity. However, the facilitates foraging and chemotaxis (Van Haastert and Bosgraaf, mechanisms of these symmetry transitions are not well understood. 2009; Li et al., 2008; Bosgraaf and Van Haastert, 2009a). We have Here, we have investigated the fundamental properties of symmetry investigated the molecular mechanism underlying these changes in and symmetry transitions of the cytoskeleton during cell movement. cell shapes. The actin-based cytoskeleton in the cortex and in Our data show that the dynamic shape changes of amoeboid cells are protrusions is the major determinant of amoeboid cell shape.
    [Show full text]
  • Geometry As Transforming Shapes
    CHAPTER 9 Geometry as Transforming Shapes Copyright © Cengage Learning. All rights reserved. SECTION 9.2 Symmetry and Tessellations Copyright © Cengage Learning. All rights reserved. Symmetry Symmetry: a transformation that places the object directly on top of itself. Chinese Yin – Yang Canadian flag "Unity of opposites" Butterfly Snowflake 3 Reflection and Rotation Symmetry 4 Reflection and Rotation Symmetry A figure has reflection symmetry if there is a line, called the line of symmetry, that can be drawn through the figure such that when we fold the paper on the line, the part of the figure on one side will lie directly on top of the other part. Imagine tracing a figure and putting the traced image directly on top of the figure. Informally, we say that the figure has rotation symmetry if we can pick up the tracing, turn it by some amount less than a full turn, and place it down so that it lies directly on the original figure. 5 Example - Reflection and Rotation Symmetry in Triangles Describe the reflection and rotation symmetries you see in the equilateral triangle, the isosceles triangle, and the scalene triangle below. 6 Example - Reflection and Rotation Symmetry in Triangles We find that the equilateral triangle has three lines of symmetry, the isosceles triangle has one line, and the scalene triangle has none. With respect to rotation symmetry, only the equilateral triangle has rotation symmetry. 7 Finding the Amount of Rotation in Rotation Symmetry 8 Finding the Amount of Rotation in Rotation Symmetry The triangle at the left in the figure below is in its original position, with the vertex angles labeled 1, 2, and 3, respectively.
    [Show full text]
  • RM - Collect the Resource Box and Homework Check Sheets and Report Slip
    RM - collect the resource box and homework check sheets and report slip. Send someone to pick up books. Facilitators - get everyone checking their homework. Remind them to show corrections. ™ Keep an eye on the time, need to Return report paper before time runs Out and then team needs to be listening. RR - fill in homework report and return to me. 24 Oct 2018 Agenda - Homework check and report submitted - Lesson 3.1.4 Facts about Isosceles triangles - Learning Log - 3.1.5 Using Transformations to make polygons - 3.51 - 3.1.6 Symmetry - Must do: 3-61,3-62, 3-65 (finish at home) - Homework 3-44 Facts about Isosceles Triangles a) Copy the B diagram and then draw A’B, the reflection of AB across line l A A’ l 3-44 Facts about Isosceles Triangles When points A B and A’ are connected, what special polygon is formed by A A’ points A, B and A’? 3-44 Facts about Isosceles Triangles When points A B and A’ are This is an connected, what isosceles special polygon triangle. is formed by A A’ points A, B and A’? 3-44 Facts about Isosceles Triangles b) What can we say about B this triangle? A A’ 3-44 Facts about Isosceles Triangles The triangle has two equal B sides since reflection is a rigid transformation. A A’ 3-44 Facts about Isosceles Triangles The line of reflection makes angle with point B and the B line segment BA that is the same as the angle between the line of reflection and BA’ A A’ 3-44 Facts about Isosceles Triangles The angles opposite the B equal sides are also equal to each other (congruent).
    [Show full text]
  • Symmetry-Based Generative Design: a Teaching Experiment
    3B-011.qxd 4/29/2013 12:28 PM Page 303 R. Stouffs, P. Janssen, S. Roudavski, B. Tunçer (eds.), Open Systems: Proceedings of the 18th International Conference on Computer-Aided Architectural Design Research in Asia (CAADRIA 2013), 303–312. © 2013, The Association for Computer-Aided Architectural Design Research in Asia (CAADRIA), Hong Kong, and Center for Advanced Studies in Architecture (CASA), Department of Architecture-NUS, Singapore. SYMMETRY-BASED GENERATIVE DESIGN: A TEACHING EXPERIMENT José Pedro SOUSA and João Pedro XAVIER University of Porto, Porto, Portugal [email protected], [email protected] Abstract. Throughout history, symmetry has been widely explored as a geometric strategy to conceive architectural forms and spaces. Nonetheless, its concept has changed and expanded overtime, and its design exploration does not mean anymore the generation of simple and predictable solutions. By framing in history this idea, the present paper discusses the relevance of exploring symmetry in architectural design today, by means of computa- tional design and fabrication processes. It confirms the emergence of a renewed interest in the topic based on two main ideas: On the one hand, symmetry-based design supports the generation of unique and apparent complex solutions out of simple geometric rules, in a bottom-up fashion. On the other hand, despite this intricacy, it assures modularity in the design components, which can bring benefits at the construction level. As the back- ground for testing and illustrating its theoretical arguments, this paper describes the work produced in the Constructive Geometry course at FAUP. Keywords. Geometry; symmetry; computational design; digital manufac- turing; education.
    [Show full text]