DOCSLIB.ORG

Smartest Report on Design of Basic Flood Barrier Prepared For: Project Officer European Commission DRAFT May 2012

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Smartest Report on Design of Basic Flood Barrier Prepared For: Project Officer European Commission DRAFT May 2012 SMARTeST Report on Design of Basic Flood Barrier Prepared for: Project Officer European Commission DRAFT May 2012 D… Flood Barrier Design Prepared by Name Cyprus Partner, under co-ordination of Antonis Toumazis, Position Cyprus Partner Signature D3.2 FReS design List of content 1 Introduction ________________________________________________________________ 4 2 The structure _______________________________________________________________ 5 3 River and Rainwater Floods ____________________________________________________ 7 3.1 Problem Definition ______________________________________________________________ 7 3.2 Hydrostatic Loading _____________________________________________________________ 7 3.3 Wind Loading __________________________________________________________________ 8 3.4 Wave Loading __________________________________________________________________ 8 3.5 Debris Impact Loading ___________________________________________________________ 9 3.6 Hydrodynamic Loading __________________________________________________________11 4 Coastal and Wave Overtopping Floods __________________________________________ 12 4.1 Problem Definition _____________________________________________________________12 4.2 Broken wave __________________________________________________________________12 5 Stress Analysis _____________________________________________________________ 14 5.1 Load Path ____________________________________________________________________14 5.2 Secondary members ____________________________________________________________14 6 Loading Combinations _______________________________________________________ 15 7 Design Tool ________________________________________________________________ 16 7.1 Bending Moments, Shear Forces __________________________________________________16 8 Examples _________________________________________________________________ 17 8.1 River / rainwater flood case ______________________________________________________17 8.2 Coastal/ Wave Overtopping flood case _____________________________________________20 9 Prototype Barrier ___________________________________________________________ 25 9.1 Development stages ____________________________________________________________25 D3.2 FReS design 4 1 Introduction During the case study for coastal flooding in Paphos Sea front area it was found that there are cases in which the requirements for flood barriers are very specific and most demanding. Potential clients and licensing authorities were raising genuine questions concerning the environment, the appearance, the traffic loading, the wave loading, the obstruction of utilities etc. There are numerous products in the market which are suitable for many applications. In cases like Paphos barrier manufacturers were prepared to listen to the project requirements and provide solutions. In order to improve the road-to-market for flood resilience technology a design tool was developed which enables consultants to design flood barriers specific to particular project requirements and derive the dimensions of the structural components. Consultants and Employers together will have the option to select non-structural components, deployment parts and water-tightness seals, depending on the flood resilience system adopted. Suppliers will be encouraged to produce innovative components, parts, seals. Contactors will be enabled to assemble and build the barriers using conventional contracts for firm designs. Figure 1-1. Flood Barrier. During normal conditions (left), During flood conditions (right) D3.2 FReS design 5 2 The structure The analysis model for the proposed barrier include s three (3) typical support conditions (figure 2-1): Hbarrier Hbarrier Hbarrier Hflood Hflood Hflood Pin - Pin Cantilever Fixed- Pin Figure 2-1. Typical barrier support arrangements (a) Pin-pin (restraint in movement at base, reaction with some flexibility to move horizontally at top) (b) Cantilever (fixed support at base, free at top) (c) Fixed-pin (fixed support at base, reaction with some flexibility to move horizontally at top) D3.2 FReS design 6 It consists from the parts as shown below : Figure 2-2. Barrier parts D3.2 FReS design 7 3 River and Rainwater Floods 3.1 Problem Definition A typical barrier arrangement is shown in figure 3-1. The barrier is raised a distance Hbarrier above pavement level. The design flood level is a distance Hflood above pavement level. The loading acting on the mounted barrier is: 1. Hydrostatic and hydrodynamic loading 2. Short surface gravity waves with a wavelength L and wave height H s, approaching at an angle β to the barrier 3. Debris impact loading, the debris having a mass m and a velocity u, at an angle δ 4. Wind loading on the barrier surface above the flood level u Barrier Hs, L Debris m u m Hbarrier Hflood Debris ä â Figure 3-1. Problem Definition Cross section (left), Plan (right) 3.2 Hydrostatic Loading The hydrostatic loading has a triangular distribution, starting at the flood level and increasing to the maximum pressure at the toe of the barrier. (figure 3-2) The maximum hydrostatic, P hydrost, pressure is equal to: Phydrost = ρ g H flood (eqn 3-2.1) D3.2 FReS design 8 Hflood P Hydrost Figure 3-2. Hydrostatic pressure Distribution 3.3 Wind Loading The barrier surface above the still (flood) water level is exposed to the wind loading. The pressure acting on the exposed surface is equal to: 2 Pwind = 0.5 ρair Vwind (eqn 3-3.1) PWind Hbarrier Hflood Figure 3-3. Wind pressure Distribution 3.4 Wave Loading Short period gravity surface waves may be generated in the flooded area due to wind or other disturbances. The wave loading may be expressed as pressure distribution along the whole length of the wetted barrier height, i.e up to elevation η* above still (flood) water level. The wave induced pressure distribution may be derived using Goda (1974) equations. D3.2 FReS design 9 p1=Pressure at crest of barrier p2=Pressure at flood level p3=Pressure at bottom support = ĕĔĥĥĜĘĥ ͯ ęğĢĢė for dz > else = (eqn 3-4.1) ͤͦ ʠ1 Ǝ Vdz ʡ ͤͥ ͂--$ - Ǝ ͂!'** ͤͦ 0 p1= ͦ (eqn 3-4.2) 0.5 ʚ1 ƍ ͗ͣͧ ʛʚ ͥ ƍ ͦ ͗ͣͧ ʛ 2 ͛ ͂ . p3=α3 p1 (eqn 3-4.3) dz (eqn 3-4.4) Ɣ 0.75 ʚ1 ƍ ͗ͣͧ ʛ͂ . xŗāęğĢĢė = ą ͦ (eqn 3-4.5) ͥ 0,6 ƍ 0,5 ʞ ʟ .$)#ʚͨ_ ęğĢĢė / ʛ (eqn 3-4.6) ͦ Ɣ 0 ͥ (eqn 3-4.7) ͕ͧ Ɣ vŗāęğĢĢė *.#ƴ ą Ƹ Where is the maximum wave height in front of the barrier = 1.8 H s (where H s is the significant ͂ . wave height) P * 2 η P1 Hbarrier Hflood P3 Figure 3-4. Wave induced pressure loading 3.5 Debris Impact Loading An accidental load that may be the critical one is debris impact loading. 3.5.1 Hard impact D3.2 FReS design 10 The force induced in case of hard impact by a mass m hitting the barrier with a velocity u at an angle δ is given by equation 3-5.1. (Annex C of Eurocode 1part 7 (EN 1991-1-7:2003). 1/2 Fdebris =u·cos δ·(m·k) (eqn 3-5.1) Where k is the equivalent elastic rigidity of debris k= E·A / L (eqn 3-5.2) m is the mass of debris m= ρ·A·L The shape of the force due to impact can be assumed as rectangular pulse of duration ∆Τ = (m/k) 1/2 thus F ·∆Τ = m·v. 3.5.2 Soft impact In case where the structure is assumed elastic and the colliding object rigid, the above formulae still apply, with k being the stiffness of the structure. If the structure is designed to absorb the impact energy by plastic deformations then it must be ensured that its ductility is sufficient to absorb the total kinetic energy 2 ½ m v r of the colliding object. 3.5.3 Rigid-plastic response In the limit case of rigid-plastic response of the structure, the above requirement is satisfied if 2 ½·m·vr ≤ F 0·y0 Where F0 is the plastic strength of the structure y0 is its defomation capacity 3.5.4 Impact force by FEMA Another equation recommended by FEMA Technical Bulletin 3-93, Non-Residential Floodproofing – Requirement and Certification for Buildings Located in Special Flood Hazard Areas in accordance with the National Flood Insurance Program is equation 2-4.3. Fi= W V / (gt) (eqn 3-5.3) Where Fi is the impact force W is the weight of the object (1000 pounds but can be reduced to 500 pounds for areas subject to minor debris flow potential. V is the velocity of the object g is the acceleration of gravity t is the duration of impact. t= 1 second in this equation Both equations are equivalent. The impact force increases with the debris mass and the debris velocity. The more flexible the barrier, the longer the duration of impact, the smaller the impact force (for the same debris mass and velocity). D3.2 FReS design 11 Equation 3-5.1 allows the user to optimise the barrier rigidity/ stiffness and thus reduce the impact force. The more the flexibility the less the rigidity, the less the force but the larger the displacements. 3.6 Hydrodynamic Loading This is the force exerted on vertical surfaces exposed to moving floodwaters. It has a triangular distribution starting with maximum value at the top of the flood and decreasing to zero at the toe of the barrier. The determination of hydrodynamic force is based on the expected velocity of the floodwaters with depths to the floodproofing design level and the shape of structure.(EN 1991-1-7:2005) 2 Fwa =0.5 k ρwa h b u (eqn 3-6.1) Where k is the shape factor (1.44 for rectangular horizontal cross section ,0.70 for circular horizontal cross section) h is the water depth b is the width of the object ρwa is the density of water u is the mean velocity of water Figure 3-5. Pressure and force due to currents D3.2 FReS design 12 4 Coastal and Wave Overtopping Floods 4.1 Problem Definition A typical barrier along the sea front is shown in figure 4-1. In such cases the design wave conditions are depth limited. The waves that overtop the sea front and impinge on the barrier are usually broken waves. The barrier is raised a distance H barrier above pavement level. The wave crest level, or the flood level, is at distance H flood above pavement level. FLOOD LEVEL Hbarrier Hflood NORMAL WATER LEVEL d Figure 4-1. Vertical Cross-section – Coastal/ Wave overtopping Flood Barrier The loading acting on the mounted barrier is: 1.
Load more

Recommended publications
  • Resilient Cambridge Summary Report
    Resilient City ↓ Resilient People This a public summary for Resilient Cambridge. 6 What is climate change? 8 What we’re doing about climate change. ↳ Closer Neighborhoods ↳ Better Buildings ↳ Stronger Infrastructure ↳ Greener City 22 How Cambridge is adapting for a resilient future. 30 Your role in our future: What you can do to help. 32 A broad view of a serious issue. 34 Let’s work together to build a Resilient Cambridge. Resilient City → Resilient People City → Resilient Resilient City of Cambridge Cambridge City of 5 While climate change poses a growing threat to our City, there are many things we can do to reduce the risk and severity of its effects. Among them: → Strengthen community → Plant more trees and organizations that provide create additional green essential services to spaces on public and residents and businesses private property to combat rising temperatures and → Make our buildings flood- energy demand and heat-resilient, and require climate-resilience → Work together with design standards on new neighboring cities and the developments state to minimize flooding What is climate change? Climate change refers to long-term changes in weather patterns that impact our environment and way of life. The science is clear: Our climate is not the same as the one that our cities were built to accommodate, and the pace of change is accelerating. Climate change will The City of Cambridge bring extreme heat, is ready to meet these severe storms, and challenges. extensive flooding. In this document, you’ll learn All three may affect our health about what needs to be done, what and comfort, cause damage to our Cambridge is already doing, and the homes and schools, and threaten our important role that you can play in access to reliable energy and safe making our City more resilient in the drinking water.
    [Show full text]
  • Kopeopeo Canal Remediation Project Flood Management Plan Condition 7.1 Resource Consent 67173
    Kopeopeo Canal Remediation Project Flood Management Plan Condition 7.1 Resource Consent 67173 BOPRC ID: A2708898 MEMORANDUM To: Brendon Love Project Manager - Kopeopeo Canal Remediation From: Peter West B.E. (Hons), CPEng, MIPENZ Date: 28 September 2017 Contract Engineer File Ref: Objective Id: Subject: Kopeopeo East Canal Remediation Project; Flood Management Plan 1 Executive Summary Bay of Plenty Regional Council has received resource consent to remove and treat contaminated sediment from within the Kopeopeo East Canal (the Canal) by a wet-dredging method. This report primarily addresses the detailed conceptual flood-management and drainage aspects of the project specific to the proposed dredging method. It is intended that this report should provide a complete treatment of the relevant material, but in places to improve readability, reference has been made to our previous and/or supporting memoranda (references at the end). This report is in two parts: Part 1 discusses relevant aspects of flood management that form necessary background material, or that have not been previously addressed – either from changes in the proposed method; or from developments in supporting information as the project has unfolded. Part 2 forms the Flood Management Plan proper, with the necessary matrix of preparation, monitoring and response procedures and actions. This flood management plan and its supporting documents (see references below) fulfil the requirements of consent condition 7.1 including all items from 7.1a through 7.1g (Resource Consent 67173; 28 September 2016). This flood management plan is consistent with the Site Management Principles and the Flood Management Principles (reproduced below) that were identified in our January 2016 memo that now form the basis of the resource consent conditions relating to flood management.
    [Show full text]
  • Baseline, Historic and Background Rates of Deposition of Lead-Rich Sediments on the Floodplain of the Coeur D’Alene River, Idaho
    In cooperation with the Coeur d’Alene Tribe Baseline, Historic and Background Rates of Deposition of Lead-Rich Sediments on the Floodplain of the Coeur d’Alene River, Idaho By Arthur A. Bookstrom1, Stephen E. Box1, Robert S. Fouseck2, John C. Wallis1, Helen Z. Kayser1 and Berne L. Jackson3 2004, revised 2013 1 USGS, 904 West Riverside Avenue, Room 202, Spokane, WA 99201 2 PO Box 2756, Auburn, AL 36831 3 Coeur d’Alene Tribe, Plummer, ID 83851 Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government Open-File Report 2004-1211, Version 1.1 U.S. Department of the Interior U.S. Geological Survey U.S. Department of the Interior Gale A. Norton, Secretary U.S. Geological Survey Charles G. Groat, Director U.S. Geological Survey, Reston, Virginia 2006 For product and ordering information: World Wide Web: http://www.usgs.gov/pubprod Telephone: 1-888-ASK-USGS For more information on the USGS—the Federal source for science about the Earth, its natural and living resources, natural hazards, and the environment: World Wide Web: http://www.usgs.gov Telephone: 1-888-ASK-USGS Although this report is in the public domain, permission must be secured from the individual copyright owners to reproduce any copyrighted material contained within this report. 2 Contents Contents .......................................................................................................................................................................................... 3 Abstract ..........................................................................................................................................................................................
    [Show full text]
  • Stop Log Flood Barriers
    PRODUCT STOP LOG FLOOD BARRIERS Flood Control International Incorporated offers removable stop log barriers that are engineered to provide similar levels of protection to permanent flood defenses, but with the distinct advantage of being fully removable when not required. They comprise aluminum panels that are inserted into steel channels. Custom made clamps compress specialist gaskets to create a reliable barrier against flood water. These stop log barriers can be supplied for virtually any configuration including arcs, closed rectangles or circles and straight runs of any length. The system can be used on slopes up to 20° and can be stepped for steeper gradients. USES Each system is load calculated based on application and the prevailing flood • Single building openings. conditions and can be configured for flood depths up to 13 feet. A four-sided • Openings in flood walls. detail is available for openings that may become fully submerged. • Stainless / aluminum system for marine environments. To facilitate installation in new builds, we can supply preformed ground plates • Fully removable perimeter defense to with integral anchors for the demountable supports. The systems can be buildings. also retrospectively fitted to suitable existing foundations in which case load • A ‘usually stored’ system for erection certified, chemically fixed sleeve anchors are used to attach the demountable when flood warnings received. supports. This leaves only stainless steel bolt blanks at each post BENEFITS location. Due to the strength of our beams, this can • Low cost system. be at 10 feet spacing. • Lightweight - sections allow safe lifting of 10ft beams by one person for rapid Purpose designed gaskets that resist silt clogging and reform even after deployment.
    [Show full text]
  • Protecting Building Utilities from Flood Damage
    FirstEdition FEMA348 November1999 Protecting BuildingUtilities HVAC FromFloodDamage PrinciplesandPracticesfortheDesign andConstructionofFloodResistant BuildingUtilitySystems FUEL ELECTRICAL SEWAGE WATER FEDERALEMERGENCYMANAGEMENTA GENCY MitigationDirectorate 500CStreet,SW Washington,DC20472 IMPORTANT If you ordered and received your copy of Protecting Building Utilites From Flood Damage directly from the FEMA Publications Center, you will automatically receive future updates. If you received your copy of Protecting Building Utilities From Flood Damage through a source other than directly from the FEMA Publications Center, you must complete the coupon below and mail it to the Center or you will not receive future updates. ............................................................................................................ Please add my name to the FEMA Mailing List FE 30 and send me updates of Protecting Building Utilities From Flood Damage Name Address City State Zip Code Fold ........................................................................................................... Place Postage Here Federal Emergency Management Agency P.O. Box 2012 Jessup, MD 20794-2012 Table of Contents CONTENTS Page CHAPTER 1 - Introduction/Overview 1.0 Introduction 1-2 1.1 How to Use this Manual 1-3 1.2 Introduction to Hazards 1-8 1.3 Basic Protection Methods 1-13 CHAPTER 2 - Regulatory Framework 2.0 Introduction 2-2 2.1 Background of the National Flood Insurance Program (NFIP) 2-2 2.2 Community Floodplain Management Permitting Process 2-5
    [Show full text]
  • Water Control Just Got Easier
    Protect Against: THE NEXT GENERATION IN FLOOD PROTECTION TM Water Control Just Got Easier Prevent Water Damage Stop Flowing Water Contain the Mess Prevent Slip & Falls Finally, a solution to these situations: Protect Against: What is the cost? • Storm preparedness • Pipe, roof & equipment leaks Property & Equipment Damage $$$ • Overflowing appliances Downtime Cost $$$ • Cafeteria accidents & spills Price of Restoration $$$ • Water runoff • A/C & refrigeration condensate control Preventing Costly • Water main breaks & sewage back up • Parking garage & elevator shaft Flood Damage PRICELESS protection & more 1 | www.quickdams.com WHY BE PREPARED? Floods are the # natural1 disaster in the United States Gate % d 2 o Feet 25 lo Absorbs Percentage of s F at ts reported work M Absorbs a 1.5 ip Quarts accidents caused r 1 M D Quart from slip and fall iverter D k a e L Pads r Absorbs A 1/8-in. pipe crack m o Da lo can result in a leak - 2 F 1.5 ta Glns rate of s Inches 250 gal/day n I ms ags Da B r 2.5 iers d te rr o 31 a Inches a B o Average number of 3.5 l W d Inches F days of missed work o o from slip and fall l F te Ga r- e 5 t Feet a W 46% of business production loss is due to water damage 2 3 CONTROL PREVENT SLIP & FALL ACCIDENTS FLUIDS Hi-Vis Gray Water Dams Activates • Absorbs water on contact & swells to create a dam when wet! • Compact & lays flat until activated & grows 2.5in high in just 5 minutes • Contain & control the flow of problem water Drip Mats Ideal for: • Absorbent Mats catch leaks, drips & spills • Condensation build up •
    [Show full text]
  • Design of Movable Weirs and Storm Surge Barriers
    InCom Working Group 26 Design of Movable Weirs and Storm Surge Barriers ----- Final Report Version 6.7 1st August 2005 Design of Movable Weirs and Storm Surge Barriers – WG26 –PIANC p. 2 SUMMARY The PIANC InCom-WG26 (Working Group) performed a - Interactions between the technical aspects of a comprehensive review (state-of-the-art) of the modern weir/barrier design with environmental and aesthetic technologies, design tools, and recent researches used to considerations (Section 5.7) design and build structures controlling water level and flow in rivers, waterways, and ports (for navigation and flood - Procedure to assess the global construction cost of a protection). weir at the design stage (Section 5.8) - Design assessment tools for preliminary and detailed The WG considered regulatory structures of river control design stages (Section 6 and Annex A) weirs and storm surge barriers, focussing on the gate design. This includes: - Prefabrication techniques (Section 7) - Gates controlling water level and flow in rivers (even - Codes, rules and standards: at national and international those not navigable) and waterways (lifting gate, tilting level; including the use of the semi-probabilistic gate, radial gate, sector, etc.; designed in one piece or Eurocode format (Section 8) with an upper flap). These are MOVABLE WEIRS. - An extensive list of relevant technical books, web sites, - Gates controlling water level and flow in estuaries with and guidelines (Section 10). regard to high tides and storms (lifting gate, articulated, tilting, rolling, floating, sliding, etc.). These are flood BARRIERS. The present hardcopy WG-26 report is a reduced version of the full report, which is available on the companion CD- The WG Report focuses on the following aspects: ROM, attached to this PIANC hardcopy report (Directory /A2- REPORT WG-26 (Extended Version)/.
    [Show full text]
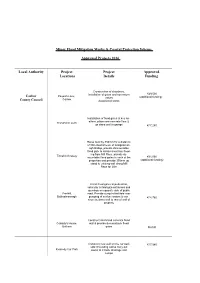
  • Minor Flood Mitigation Works & Studies Scheme (Non-Coastal )
    Minor Flood Mitigation Works & Coastal Protection Scheme Approved Projects 2016 Local Authority Project Project Approved Locations Details Funding Construction of chambers, installation of gates and non-return €49,500 Carlow Paupish Lane, valves (additional funding) Carlow County Council Associated works Installation of flood gates at key loc- ations, place new concrete floor & Tinnahinch Loch up stand wall in garage €17,280 Raise level by 350mm for a distance of 80m downstream of Graignaman- agh Bridge, provide demountable flood gate to isolate area from flood- ing from Mill Race, provide de- Tinnahinch Quay mountable flood gates to each of the €31,050 properties and provide 350mm up (additional funding) stand to existing wall along Mill Race for 20m Install flood gates at pedestrian, vehicular & field gate entrances and openings on opposite side of public Fonthill, road. Provide sump to facilitate over Ballinabrannagh pumping of surface waters & con- €14,760 struct buttress wall to rear of wall of property Construct reinforced concrete flood Cassidy's House, wall & provide demountable flood Gotham gates €6,030 Construct new wall on the car park €17,985 side of existing wall & carry out Kennedy Car Park works to include drainage and sumps Removal of trees Clare Reconstruction of embankment- set back from channel edge, graded at County Council Mountcatherine €49,500 approximately 1:3 on both sides and flat on top (width of 1.5 to 2m) Associated works Tree & shrub removal from Inchinossig Bridge to the Bunsheelin River, on Bunsheelin River
    [Show full text]
  • Mosquito Creek Debris Flood Barrier – the First Line of Defence in Protecting the Public from Geohazards
    Mosquito Creek Debris Flood Barrier – The First Line of Defence in Protecting the Public from Geohazards Charles Hunt, M.Sc., P.Eng., ACSM., Jamie Stirling, M.Sc., P.Geo., Jack Price, EIT., ACSM Tetra Tech EBA, Vancouver, BC, Canada Fiona Dercole, Michelle Weston District of North Vancouver, North Vancouver, BC, Canada ABSTRACT In the District of North Vancouver, the Mosquito Creek watershed drains water from Grouse and Fromme Mountains through a densely populated residential area down to Burrard Inlet. The upper part of the watershed has had a number of landslides which have the potential to create debris floods, a significant geohazard to the residents of North Vancouver. The District of North Vancouver (DNV) requested the design and installation of a debris flood barrier at an optimal point on Mosquito Creek. Critical to this installation was careful sizing of the barrier for a 200-year debris flood event, locating the barrier within a fish bearing creek containing rare long tailed frogs and providing the most cost effective solution to the DNV. This paper presents the investigation of the mainstem of Mosquito Creek, including a detailed geohazard inventory map documenting notable features such as; significant sediment sources, natural barriers, landslides, bedrock canyons, waterfalls and debris jams. The paper also details some of the engineering design undertaken to construct the debris net within a bedrock canyon. The flexible net debris barrier at Mosquito Creek is only the second barrier of this type to be installed in British Columbia and when compared to alternatives is more cost effective, less intrusive and more easily repaired, making it a more sustainable solution.
    [Show full text]
  • Joint Emergency Action Plan for Severe Storm and Flood Response in City of San José
    Joint Emergency Action Plan for Severe Storm and Flood Response in City of San José Last Revised: December 2018 (THIS PAGE INTENTIONALLY LEFT BLANK) Joint Emergency Action Plan for Severe Storm and Flood Response in City of San José MC14104 December 2018 EXECUTIVE SUMMARY—JOINT EMERGENCY ACTION PLAN The first version of the Joint Emergency Action Plan for Severe Storm and Flood Response in City of San Jose (EAP) was approved by the Santa Clara Valley Water District (District) Board of Directors and San Jose City (City) Council at a joint meeting held on November 3, 2017. The EAP provided guidance on how the District and City would coordinate, communicate, and make decisions during storm and flood events and established a new method of classifying Flood Emergency Operational and Severity Levels. Since there was flooding on Coyote Creek in February of 2017, the EAP included an appendix of specific guidance related to Coyote Creek. The EAP is to be reviewed and/or exercised annually and updated/revised as appropriate. The District Board of Directors and San Jose City Council delegated approval authority for updates and revisions of the EAP to the City Manager and District Chief Executive Officer (CEO) or their designee. In addition to an annual review and revision of the EAP in 2018, three new appendices are being added to provide specific guidance related to flood risks on Guadalupe River, Canoas Creek and Ross Creek. The 2018 review and update to the EAP was initiated in April under the direction of a Joint Management Team and continues to be based on the concept of a Multi-Agency Coordination (MAC) Group.
    [Show full text]
  • The Impact of Flooding on Aquatic Ecosystem Services
    Biogeochemistry https://doi.org/10.1007/s10533-018-0449-7 The impact of flooding on aquatic ecosystem services Ceara J. Talbot . Elena M. Bennett . Kelsie Cassell . Daniel M. Hanes . Elizabeth C. Minor . Hans Paerl . Peter A. Raymond . Rodrigo Vargas . Philippe G. Vidon . Wilfred Wollheim . Marguerite A. Xenopoulos Received: 20 October 2017 / Accepted: 27 April 2018 Ó The Author(s) 2018 Abstract Flooding is a major disturbance that people through freshwater aquatic ecosystem services, impacts aquatic ecosystems and the ecosystem ser- which often go unrecognized because they are less vices that they provide. Predicted increases in global evident and can be difficult to evaluate. Here, we flood risk due to land use change and water cycle identify the effects that small magnitude frequently intensification will likely only increase the frequency occurring floods (\ 10-year recurrence interval) and and severity of these impacts. Extreme flooding events extreme floods ([ 100-year recurrence interval) have can cause loss of life and significant destruction to on ten aquatic ecosystem services through a system- property and infrastructure, effects that are easily atic literature review. We focused on ecosystem recognized and frequently reported in the media. services considered by the Millennium Ecosystem However, flooding also has many other effects on Assessment including: (1) supporting services (pri- mary production, soil formation), (2) regulating ser- vices (water regulation, water quality, disease Responsible Editor: Sujay Kaushal. regulation, climate regulation), (3) provisioning ser- Electronic supplementary material The online version of vices (drinking water, food supply), and (4) cultural this article (https://doi.org/10.1007/s10533-018-0449-7) con- services (aesthetic value, recreation and tourism).
    [Show full text]
  • Flood Guide for Homeowners
    Homeowners guide to flood resilience A living document Homeowners guide to flood resilience: a living document A SECTION ONE SECTION THREE Learn about your flood risk 2 Protecting your home 20 Why should I think about flood risk? 3 The flood protection product information tables 21 Flood Re 4 Permanent resistance 22 What is the risk to houses from flooding? 6 Temporary resistance 27 How do I find out if my home Ancillary products 30 is at risk from flooding? 7 Resilience 34 Should I consider protecting Community solutions 38 my home from flooding? 8 How best to protect myself, my family and my home from flooding 10 SECTION FOUR Sustainable drainage solutions 42 Another piece of the jigsaw: ‘SuDS’ 43 SECTION TWO Flood expertise around the UK 16 Who does what in the UK? 17 SECTION FIVE Contents Contents Case studies 46 SECTION SIX Directory of manufacturers 72 This guide is best viewed using Adobe Acrobat. To download a free version of this application visit www.get.adobe.com/uk/reader/ B Homeowners guide to flood resilience: a living document Foreword Having been flooded ourselves, we know that flooding can This guide which is written especially with the home have a devastating impact on homes and families. This owner in mind hopes to reduce the worry about what was clearly shown by the terrible floods caused by storms flood protection products to use, and illustrates the Desmond, Eva and Frank in December 2015 and January variety of ways a home can be protected, how dificult 2016, which hit northern England and parts of Scotland, the product is to fit and when it is appropriate to Wales and Ireland.
    [Show full text]