Solvency II's One-Year Time Horizon
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

2020-2021 Districtwide School Year Calendar
FINAL 2020 – 2021 Districtwide School Year Calendar AUGUST FEBRUARY 2020-21 Calendar M T W T F M T W T F 3 4 5 6 7 1 2 3 4 5 Aug 17 Professional Meeting Day. No Students 8 Aug 18 -21 Staff Professional Development Day. 10 11 12 13 14 9 10 11 12 M No Students. Aug 24 Schools Open. Students Report. 17 18 19 20 21 15 16 17 18 19 Sept 7 Labor Day. Holiday. Schools Closed Sep 14 Midterm Week 24 25 26 27 28 22 23 24 25 26 Sep 21 –Oct 9 Fall Gifted Screening 31 Sep 28- Oct 9 INVIEW / Terra Nova (Elementary) Oct 14 PSAT (High Schools) Oct 16 End of First Quarter. Students Report. SEPTEMBER MARCH (39 Instructional Days, 44 Staff Days). M T W T F M T W T F Oct 21 – 27 3rd Grade Fall ELA. 1 2 3 4 1 2 3 4 5 Nov 2 Conference Comp Day –School Closed Nov 3 Election Day – Conference Day. 7 8 9 10 11 8 9 10 11 12 Q No Students. 14 M 15 16 17 18 15 16 17 18 19 Nov 9 Midterm Week 21 22 23 24 25 22 23 24 25 26 Nov 11 Veterans’ Day. Holiday Observance. Schools Closed. 28 29 30 29 30 31 Nov 25 Conference Day. No Students. Nov 26 Thanksgiving. Holiday Observance. OCTOBER APRIL Nov 27 Schools Closed. Dec 1 – 11 Fall HS End of Course M T W T F M T W T F Dec 14 -18 Semester 1 Exams (High Schools) 1 2 1 2 Dec 18 End of Second Quarter. -

The Mathematics of the Chinese, Indian, Islamic and Gregorian Calendars
Heavenly Mathematics: The Mathematics of the Chinese, Indian, Islamic and Gregorian Calendars Helmer Aslaksen Department of Mathematics National University of Singapore [email protected] www.math.nus.edu.sg/aslaksen/ www.chinesecalendar.net 1 Public Holidays There are 11 public holidays in Singapore. Three of them are secular. 1. New Year’s Day 2. Labour Day 3. National Day The remaining eight cultural, racial or reli- gious holidays consist of two Chinese, two Muslim, two Indian and two Christian. 2 Cultural, Racial or Religious Holidays 1. Chinese New Year and day after 2. Good Friday 3. Vesak Day 4. Deepavali 5. Christmas Day 6. Hari Raya Puasa 7. Hari Raya Haji Listed in order, except for the Muslim hol- idays, which can occur anytime during the year. Christmas Day falls on a fixed date, but all the others move. 3 A Quick Course in Astronomy The Earth revolves counterclockwise around the Sun in an elliptical orbit. The Earth ro- tates counterclockwise around an axis that is tilted 23.5 degrees. March equinox June December solstice solstice September equinox E E N S N S W W June equi Dec June equi Dec sol sol sol sol Beijing Singapore In the northern hemisphere, the day will be longest at the June solstice and shortest at the December solstice. At the two equinoxes day and night will be equally long. The equi- noxes and solstices are called the seasonal markers. 4 The Year The tropical year (or solar year) is the time from one March equinox to the next. The mean value is 365.2422 days. -

2021-22 Official District Calendar
Perrysburg AMENDED JUNE 21, 2021 Public Schools Tuesday August 10 HPI - Grade 6 orientation, Junior High Orientation 2021-2022 Wednesday August 11 JH &HPI (grade 5) orientation Thursday August 12 Teacher Inservice School Year Calendar Friday August 13 Teacher Inservice Monday August 16 Teacher Inservice/Workday Tuesday-Thursday August 17-19 Elementary - Jacket Jump Start Appointments Tuesday August 17 HS-Freshman only attend, JH-Grade 8 only attend, HPI-Grade 6 only attend AUGUST 2021 SEPTEMBER 2021 OCTOBER 2021 Wednesday August 18 HS-Freshman only attend, JH-Grade 7 only attend, HPI-Grade 5 only attend M T W T F M T W T F M T W T F Thursday August 19 All High School, Junior High and HPI attend school 2 3 4 5 6 1 2 3 1 Thursday August 19 High School Open House - evening Elementary - First day 9 10 11 12 13 6 7 8 9 10 4 5 6 7 8 Friday August 20 Monday August 23 Preschool First Day 16 17 18 19 20 13 14 15 16 17 11 12 13 14 15 1 Thursday August 26 Junior High Open House - evening 23 24 25 26 27 20 21 22 23 24 18 19 20 21 22 Monday September 6 Labor Day - No School Preschool-12 30 31 27 28 29 30 25 26 27 28 29 Thursday September 23 High School Evening Conferences NOVEMBER 2021 DECEMBER 2021 JANUARY 2022 Friday October 15 End of first quarter M T W T F M T W T F M T W T F Monday & Wed. -

Critical Analysis of Article "21 Reasons to Believe the Earth Is Young" by Jeff Miller
1 Critical analysis of article "21 Reasons to Believe the Earth is Young" by Jeff Miller Lorence G. Collins [email protected] Ken Woglemuth [email protected] January 7, 2019 Introduction The article by Dr. Jeff Miller can be accessed at the following link: http://apologeticspress.org/APContent.aspx?category=9&article=5641 and is an article published by Apologetic Press, v. 39, n.1, 2018. The problems start with the Article In Brief in the boxed paragraph, and with the very first sentence. The Bible does not give an age of the Earth of 6,000 to 10,000 years, or even imply − this is added to Scripture by Dr. Miller and other young-Earth creationists. R. C. Sproul was one of evangelicalism's outstanding theologians, and he stated point blank at the Legionier Conference panel discussion that he does not know how old the Earth is, and the Bible does not inform us. When there has been some apparent conflict, either the theologians or the scientists are wrong, because God is the Author of the Bible and His handiwork is in general revelation. In the days of Copernicus and Galileo, the theologians were wrong. Today we do not know of anyone who believes that the Earth is the center of the universe. 2 The last sentence of this "Article In Brief" is boldly false. There is almost no credible evidence from paleontology, geology, astrophysics, or geophysics that refutes deep time. Dr. Miller states: "The age of the Earth, according to naturalists and old- Earth advocates, is 4.5 billion years. -

The Throughput Year Clock: Defining “One Year” for AB 705
The Throughput Year Clock: Defining “one year” for AB 705 December 2020 | www.rpgroup.org The term “throughput” refers to the percentage of a student cohort who complete a course sequence within a set period after having begun that sequence at the same point in time. Under AB 705 the set period for observing throughput rates is described in law as “one year”. While that time frame seems intuitive enough, the operational definition of “one year” (or the “year clock”) has varied somewhat across sources. For instance, the operational definition of the year clock used by MMAP has evolved over time and been refined. This document provides an overview of how the MMAP team defined the year clock prior to September 2020, as well as a revised definition of the year clock that the team implemented in September 2020. Additionally, it is argued that consistency across cohorts of students with different starting terms within reports is more critical than maintaining a problematic definition simply for future reports to use the same definition as historical reports. Previously Used Throughput Timeframes For the purposes of AB 705 research, a year has been defined as two primary terms plus one or two minor terms or three primary terms (for quarter-based colleges). A minor term such as summer or winter intersession may be included in the three primary term sequence because its inclusion is necessary to satisfy the three primary terms requirement. Summer is a minor term for both the quarter and semester systems, whereas winter intersession is only considered a minor term for semester systems. -

2021-2022 School Year Calendar June 2021 June 21-July 29 - Summer School 17 - Martin Luther King Jr
2021-2022 School Year Calendar June 2021 June 21-July 29 - Summer school 17 - Martin Luther King Jr. Day January 2022 (Fridays off) S M T W T F S 27 - Second Quarter Ends S M T W T F S 1 2 3 4 5 28 - Teacher Record Keeping Day 1 6 7 8 9 10 11 12 31 - Third Quarter Begins 2 3 4 5 6 7 8 13 14 15 16 17 18 19 9 10 11 12 13 14 15 20 21 22 23 24 25 26 16 17 18 19 20 21 22 27 28 29 30 23 24 25 26 27 28 29 30 31 July 2021 4 - Independence Day S M T W T F S June 21-July 29 - Summer school 21 - Presidents Day February 2022 (Fridays off) 1 2 3 22 - Parent Teacher Conferences S M T W T F S 4 5 6 7 8 9 10 1 2 3 4 5 11 12 13 14 15 16 17 6 7 8 9 10 11 12 18 19 20 21 22 23 24 13 14 15 16 17 18 19 25 26 27 28 29 30 31 20 21 22 23 24 25 26 27 28 August 2021 19-20 - New Teacher Orientation* S M T W T F S Aug. 23-Sept. 3 - Teacher Prep/PD Days* 31 - Third Quarter Ends March 2022 1 2 3 4 5 6 7 S M T W T F S 8 9 10 11 12 13 14 1 2 3 4 5 15 16 17 18 19 20 21 6 7 8 9 10 11 12 22 23 24 25 26 27 28 13 14 15 16 17 18 19 29 30 31 20 21 22 23 24 25 26 27 28 29 30 31 September 2021 Aug. -

Calculating Percentages for Time Spent During Day, Week, Month
Calculating Percentages of Time Spent on Job Responsibilities Instructions for calculating time spent during day, week, month and year This is designed to help you calculate percentages of time that you perform various duties/tasks. The figures in the following tables are based on a standard 40 hour work week, 174 hour work month, and 2088 hour work year. If a recurring duty is performed weekly and takes the same amount of time each week, the percentage of the job that this duty represents may be calculated by dividing the number of hours spent on the duty by 40. For example, a two-hour daily duty represents the following percentage of the job: 2 hours x 5 days/week = 10 total weekly hours 10 hours / 40 hours in the week = .25 = 25% of the job. If a duty is not performed every week, it might be more accurate to estimate the percentage by considering the amount of time spent on the duty each month. For example, a monthly report that takes 4 hours to complete represents the following percentage of the job: 4/174 = .023 = 2.3%. Some duties are performed only certain times of the year. For example, budget planning for the coming fiscal year may take a week and a half (60 hours) and is a major task, but this work is performed one time a year. To calculate the percentage for this type of duty, estimate the total number of hours spent during the year and divide by 2088. This budget planning represents the following percentage of the job: 60/2088 = .0287 = 2.87%. -

'IOLANI SCHOOL 2021-2022 Year-At-A-Glance (Subject to Change) Check for Calendar Changes/Updates
'IOLANI SCHOOL 2021-2022 Year-at-a-Glance (Subject to Change) Check www.iolani.org for Calendar Changes/Updates 2021 Monday, August 16 Residential Life New Student Arrival and Registration Thursday, August 19 Residential Life Returning Student Arrival and Registration Tuesday, August 24 FIRST DAY of 2021-2022 School Year Monday, September 6 Labor Day | School Holiday (Offices Closed) Monday, September 27 Head of School Holiday (Offices Closed) Monday, October 11 Discoverers' Day | School Holiday (Offices Closed) Wednesday, October 13 PSAT Exam/Faculty Professional Development Day | US Early Dismissal/No LS Classes Friday, October 22 Fall Break | No US/LS Classes (Offices OPEN) Friday, October 29 K-3 Parent-Teacher Conferences | No K-3 Classes Friday, November 5 K-3 Parent-Teacher Conferences | No K-3 Classes Thursday, November 11 Veterans' Day | School Holiday (Offices Closed) Wednesday, November 24 Residence Hall Closes at 6:00 pm Thursday, November 25 Thanksgiving Day | Campus Closed-No Events Friday, November 26 Thanksgiving Holiday | School Holiday (Offices Closed) Saturday, November 27 Residence Hall Opens at 8:00 am Friday, December 17 Christmas Vacation Begins (Offices OPEN) Friday, December 17 Residence Hall Closes at 4:00 pm 2022 Saturday, January 1 Residence Hall Opens at 8:00 am Monday, January 3 School Resumes Thursday, January 13 US Semester Exams/LS Faculty Professional Development Day (No US/LS Classes) Friday, January 14 US Semester Exams/LS Faculty Work Day (No US/LS Classes) Monday, January 17 Martin Luther King Jr. -

2020–2021District Calendar
2020–2021 DISTRICT CALENDAR August 10-14 ...........................New Leader Institute November 11 .................... Veterans Day: No school Major Religious & Cultural Holidays August 17-20 ........ BPS Learns Summer Conference November 25 ..... Early release for students and staff 2020 2021 (TSI, ALI, English Learner Symposium, November 26-27 ....Thanksgiving Recess: No school July 31 ..........Eid al-Adha Jan. 1 ........New Year’s Day Early Childhood/UPK Conference, December 24- January 1 ..Winter Recess: No school Sep. 19-20 ..Rosh Hashanah Jan. 6 ......Three Kings Day New Teacher Induction) January 4.................... All teachers and paras report . Sep. 28 .........Yom Kippur Feb. 12 .... Lunar New Year September 1 ......REMOTE: UP Academies: Boston, January 5...................... Students return from recess Nov. 14 ...... Diwali begins Feb. 17 ... Ash Wednesday Dorchester, and Holland, January 18..................M.L. King Jr. Day: No school all grades − first day of school Nov. 26 .......Thanksgiving Mar. 27-Apr. 3 ..... Passover February 15 .................... Presidents Day: No school September 7 .......................... Labor Day: No school Dec. 10-18 .......Hanukkah Apr. 2 ............ Good Friday February 16-19.............February Recess: No school September 8 .............. All teachers and paras report Dec. 25 ............Christmas Apr. 4 ...................... Easter April 2 ...................................................... No school September 21 ..........REMOTE: ALL Students report Dec. -
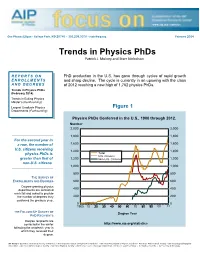
Trends in Physics Phds Patrick J
www.aip.org/statistics One Physics Ellipse • College Park, MD 20740 • 301.209.3070 • [email protected] February 2014 Trends in Physics PhDs Patrick J. Mulvey and Starr Nicholson REPORTS ON PhD production in the U.S. has gone through cycles of rapid growth ENROLLMENTS and sharp decline. The cycle is currently in an upswing with the class AND DEGREES of 2012 reaching a new high of 1,762 physics PhDs. Trends in Physics PhDs (February 2014) Trends in Exiting Physics Master’s (Forthcoming) Largest Graduate Physics Figure 1 Departments (Forthcoming) Physics PhDs Conferred in the U.S., 1900 through 2012. Number 2,000 2,000 1,800 1,800 For the second year in a row, the number of 1,600 1,600 U.S. citizens receiving 1,400 1,400 physics PhDs is Total U.S. Citizens greater than that of 1,200 Non-U.S. Citizens 1,200 non-U.S. citizens. 1,000 1,000 800 800 THE SURVEY OF ENROLLMENTS AND DEGREES 600 600 Degree-granting physics 400 400 departments are contacted each fall and asked to provide the number of degrees they 200 200 conferred the previous year. 0 0 1900 10 20 30 40 50 60 70 80 90 00 12 THE FOLLOW-UP SURVEY OF Degree Year PHD RECIPIENTS Degree recipients are contacted in the winter http://www.aip.org/statistics following the academic year in which they received their degree. AIP Member Societies: Acoustical Society of America • American Association of Physicists in Medicine • American Association of Physics Teachers • American Astronomical Society • American Crystallographic Association • American Meteorological Society • American Physical Society • AVS Science and Technology of Materials, Interfaces and Processing • The Optical Society • The Society of Rheology Page 2 focus on Trends in Physics PhDs This focus on provides an in-depth analysis of physics PhD production in the U.S. -
![Work Year Calendar [PDF]](https://docslib.b-cdn.net/cover/0109/work-year-calendar-pdf-1080109.webp)
Work Year Calendar [PDF]
PERSONNEL SUPPORT SERVICES DEPARTMENT EMPLOYEE WORK START/END DATES 2021-2022 SCHOOL YEAR POWAY FEDERATION OF TEACHERS (PFT) Employee Contract Year Start Date End Date 186 Contract Days 8/16/2021 6/10/2022 Abraxas High School 7/13/2021 6/22/2022 Valley Elementary School 7/28/2021 6/10/2022 New Teachers 8/12/2021 6/10/2022 (8/12/2021 & 8/13/2021 New Teacher Day/Prep) Certificated Librarians 8/03/2021 6/23/2022 POWAY SCHOOL EMPLOYEES ASSOCIATION (PSEA) UNIT I AND UNIT II Employee Contract Year Start Date* End Date 9.5 months (185 work days) 8/16/2021 6/09/2022 10 months (195 work days) 8/05/2021 6/14/2022 10.5 months (202 work days) 8/03/2021 6/21/2022 11 months (209 work days) 8/02/2021 6/29/2022 11.5 months (220 work days) 7/19/2021 6/30/2022 12 months (244 work days) 7/01/2021 6/30/2022 (**7/02/2021 non workday, non-paid) *With mutual agreement between the supervisor and the employee, the start and end date may be modified. Notification to the Payroll Department is required. **PUSD salary schedules are based on 260 workdays per year. The 2021-2022 school year contains 261 possible work days. As a result, 12-month employees will have one non-paid non-workday in July (July 2). Transportation may have out of district schools in session on July 1 & July 2 which some staff will work on an optional basis: Operations (Schedulers/Supervisors), Safety & Training and Shop Staff (mechanics). -

Working Towards a Coordinated Effort in Science
A TIME FOR PHYS I CS FI RS T AC A DEMY FOR TE A CHERS - INQU I RY A ND MODEL I NG EXPER I ENCES FOR PHYS I CS FI RS T For 9th grade science teachers NEWSLETTER: Vol 1, No. 2, August 2007 CON te N T S PHYS I CS FI RS T DUR I NG Physics First during the Academic Year����������������������������������1 T H E C A D emi C ea R Spend June with Physics First ������������������������������������������������2 A Y The Star Farm �������������������������������������������������������������������������3 Sara Torres, Columbia Public Schools End-of-Course Assessments ���������������������������������������������������4 Notebooking ����������������������������������������������������������������������������5 Working Towards a Coordinated Effort in Science and Math he 2007 Physics First Summer Academy was a Education ���������������������������������������������������������������������������������6 Twonderful learning opportunity by all who partici- Physics First - The Second Time Around��������������������������������7 pated. During the academy, 50 teachers returned for A Special Visit by a Physics First Pioneer �������������������������������8 year 2, 22 protégés attended the academy for 4 weeks, From Math Teacher to Physics Protégé ����������������������������������9 12 math teachers attended one week, and 14 adminis- Melissa Reed, Webb City R-7 ��������������������������������������������������9 trators attended two days. In addition, Dr. Leon Leder- Physics First Participation Yields Gains for Teachers and Stu- man, Physics Nobel Prize Winner, visited