Accounting for Regional Poverty Differences in Croatia: Exploring the Role of Disparities in Average Income and Inequality
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

FEEFHS Journal Volume VII No. 1-2 1999
FEEFHS Quarterly A Journal of Central & Bast European Genealogical Studies FEEFHS Quarterly Volume 7, nos. 1-2 FEEFHS Quarterly Who, What and Why is FEEFHS? Tue Federation of East European Family History Societies Editor: Thomas K. Ecllund. [email protected] (FEEFHS) was founded in June 1992 by a small dedicated group Managing Editor: Joseph B. Everett. [email protected] of American and Canadian genealogists with diverse ethnic, reli- Contributing Editors: Shon Edwards gious, and national backgrounds. By the end of that year, eleven Daniel Schlyter societies bad accepted its concept as founding members. Each year Emily Schulz since then FEEFHS has doubled in size. FEEFHS nows represents nearly two hundred organizations as members from twenty-four FEEFHS Executive Council: states, five Canadian provinces, and fourteen countries. lt contin- 1998-1999 FEEFHS officers: ues to grow. President: John D. Movius, c/o FEEFHS (address listed below). About half of these are genealogy societies, others are multi-pur- [email protected] pose societies, surname associations, book or periodical publish- 1st Vice-president: Duncan Gardiner, C.G., 12961 Lake Ave., ers, archives, libraries, family history centers, on-line services, in- Lakewood, OH 44107-1533. [email protected] stitutions, e-mail genealogy list-servers, heraldry societies, and 2nd Vice-president: Laura Hanowski, c/o Saskatchewan Genealogi- other ethnic, religious, and national groups. FEEFHS includes or- cal Society, P.0. Box 1894, Regina, SK, Canada S4P 3EI ganizations representing all East or Central European groups that [email protected] have existing genealogy societies in North America and a growing 3rd Vice-president: Blanche Krbechek, 2041 Orkla Drive, group of worldwide organizations and individual members, from Minneapolis, MN 55427-3429. -

Croatia. 'Virovitica on Cadastral Maps'
CO-295 VIROVITICA ON CADASTRAL MAPS KICINBACI S. State geodetic administration, VIROVITICA, CROATIA Virovitica is a town in northern Croatia with a population of 15,000. The town is situated in the valley of the Drava river, in the southern part of the Pannonian Basin. The year 1234, when Virovitica was made a free trade town, is regarded the town’s founding year. The regular form of Virovitica indicates that the town was founded on a crossroads of two important traffic routes. The first route runs from the West to the East parallel with the Drava river, which is a tributary to the Danube; the second route runs from the North to the South. Being situated near the Hungarian border Virovitica also has a Hungarian name – Veröcé, which means “a small door”, a name that reminds of that there is a passage there from the Drava river valley to the Sava river valley through the Bilogora mountainous range. Some of the wealthy landowners had made the maps of their own estates even before any systematic survey was done, but these maps are not dealt with in this paper. The subject matter here is the systematic surveys and maps that are the result of the surveys. My wish was to analyse our cartographic heritage and link it with modern technologies. THE 19th CENTURY The Virovitica Town Museum keeps some of the cadastral records from the time of Emperor Joseph II, when the survey of the 18th century locality of Virovitica was carried out. This preserved data does not contain any graphic supplements. -

Karlovačka Županija Najjača Je «Bike&Bed» Destinacija Ne Samo Kontinentalnog Dijela Već Cijele Hrvatske
gradova: KARLOVAC, DUGA RESA, OGULIN, OZALJ, SLUNJ 5 Karlovac. Mjesto susreta u kojem se susreću kontinentalna i mediteranska Hrvatska jest administrativno i gospodarsko središte županije. U sjecištu riječnih tokova Kupe, Korane, Mrežnice i Dobre, smješten u u središnjoj Hrvatskoj, jedan je od najvažnijih prometnih čvorišta u Hrvatskoj. Kroz grad prolaze željeznički i cestovni pravci koji povezuju Jadan i Podunavlje. Duga Resa. Smještena uz rijeku Mrežnicu i na prometno značajnoj sastavnici hrvatskog kopna i mora. TuKARLOVAC, prolaze prometni OGULIN, pravci Karolina SLUNJ, i Jozefina DUGA koji RESA,su ucrtali OZALJ osnovne pravce povezanosti hrvatske unutrašnjosti i primorja. Ogulin. U samom središtu hrvatske potkove, između centara Zagreba i Rijeke, smjestio se grad Ogulin. Uz kulturno-povijesnu baštinu ovaj grad bajki poznat je i kao grad sa nevjerojatno lijepom okolicom / gora čudesnog oblika i zastrašujuće ljepote –Klek, prekrasne rijeke Dobra i Mrežnica kao i Jezero Sabljaci . Ozalj. Uz granicu sa Slovenijom nalazi se grad Ozalj. Dobro je cestovno i željeznički povezan te stoga ima dobre uvjete za međudržavnu pograničnu suradnju. Svoj gospodarski razvoj temelji na iskorištavanju prirodnih resursa. Slunj. Na magistralnoj cesti koja povezuje Zagreb sa srednjim i južnim Jadranom, uz rijeku Koranu smješten je grad Slunj. Zahvaljujući ruralnim karakteristikama i okruženju, razvija se uslužna djelatnost-turizam, trgovina, ugostiteljstvo, te obrtništvo i ekološki čiste industrije. Njegovu prepoznatljivost čine Rastoke-prirodni fenomen sa mnoštvo slapova, brzaca, kaskada i malih jezera. rijeke: DOBRA, MREŽNICA, KUPA, KORANA 4 Naše rijeke , netaknuti prirodni biseri pružaju posebne doživljaje za ljubitelje izvorne ljepote. Uz ribolov, splavarenje, lov i boravak u zdravim planinskim zračnim lječilištima pravi su raj u oazi mira i odmora. -

JANAF Oil Pipeline & Storage Company
JANAF Oil Pipeline & Storage Company JANAF IN EUROPEAN OIL PIPELINE NETWORK 2 JANAF pipeline has significant role in oil supply to refineries of SE & Central Europe 1979-2014 - 201 mil. tons , oil transport JANAF JANAF – ADRIA PIPELINES EU PROJECT OF COMMON INTEREST 3 JANAF is recognized as EU strategic pipeline through project of common interest entitled JANAF-Adria pipelines: reconstruction, upgrade, maintenance and capacity increase of the existing JANAF and Adria oil pipelines linking Croatian Omišalj seaport to the Southern Druzhba JANAF – Adria is one of six oil pipelines PCI and one of 248 energy PCI adopted by EC in 2013 Promoters of the PCI are JANAF (Croatia), MOL (HU) and Transpetrol (SK) JANAF OIL PIPELINE ALLOWS FREE FLOW OF CRUDE OIL ACROSS BORDERS AND SECURE SUPPLY IN EU AND SE EUROPEAN COUNTRIES ENERGY UNION PRINCIPLE 4 Refinery capacities (MT): Total 37,7 MT Rijeka (Croatia) 4,5 Sisak (Croatia) 2,2 Pancevo (Serbia) 4,8 Novi Sad (Serbia) 2,5 Brod (Bosnia and Herz.) 1,3 Szazhalombatta (Hungary) 8,1 Slovnaft (Slovakia) 6,1 Kralupy & Lilvinov (Czech R.) 8,2 JANAF STORES COMPULSORY CRUDE OIL & PETROLEUM PRODUCTS STOCKS 5 Omišalj Terminal 240.000 m3 (crude oil) Sisak Terminal 240.000 m3 (crude oil) Žitnjak, Zagreb Terminal 100.000 m3 (petrolum products) Small shareholders DUUDI / DAB JANAF OIL PIPELINE & 5% 4% HEP 5% DUUDI / RH DUUDI / STORAGE SYSTEMS 11% HZMO 37% COMPANY PROFILE INA 12% 6 CERP 26% JANAF Plc. performs the activities of crude oil transport, as well as storage and reloading of crude oil and petroleum products Designed capacity - 34 million tons of crude oil transported annually (MTA), while the installed capacity amounts to 20 MTA Length of pipeline - 622 km Omišalj-Urinj subsea oil pipeline linking Omišalj Terminal and INA- Oil Refinery Rijeka Reversal flow on the Sisak-Coatian/Hungarian border-Sisak and Omišalj-Sisak sections (permitting procedure under way) Terminals: Crude oil: Omišalj, Sisak, Virje, Slavonski Brod Capacities:1,540 mil. -

Oligarchs, King and Local Society: Medieval Slavonia
Antun Nekić OLIGARCHS, KING AND LOCAL SOCIETY: MEDIEVAL SLAVONIA 1301-1343 MA Thesis in Medieval Studies Central European University CEU eTD Collection Budapest May2015 OLIGARCHS, KING AND LOCAL SOCIETY: MEDIEVAL SLAVONIA 1301-1343 by Antun Nekić (Croatia) Thesis submitted to the Department of Medieval Studies, Central European University, Budapest, in partial fulfillment of the requirements of the Master of Arts degree in Medieval Studies. Accepted in conformance with the standards of the CEU. ____________________________________________ Chair, Examination Committee ____________________________________________ Thesis Supervisor ____________________________________________ Examiner CEU eTD Collection ____________________________________________ Examiner Budapest Month YYYY OLIGARCHS, KING AND LOCAL SOCIETY: MEDIEVAL SLAVONIA 1301-1343 by Antun Nekić (Croatia) Thesis submitted to the Department of Medieval Studies, Central European University, Budapest, in partial fulfillment of the requirements of the Master of Arts degree in Medieval Studies. Accepted in conformance with the standards of the CEU. CEU eTD Collection ____________________________________________ External Reader Budapest Month YYYY OLIGARCHS, KING AND LOCAL SOCIETY: MEDIEVAL SLAVONIA 1301-1343 by Antun Nekić (Croatia) Thesis submitted to the Department of Medieval Studies, Central European University, Budapest, in partial fulfillment of the requirements of the Master of Arts degree in Medieval Studies. Accepted in conformance with the standards of the CEU. ____________________________________________ External Supervisor CEU eTD Collection Budapest Month YYYY I, the undersigned, Antun Nekić, candidate for the MA degree in Medieval Studies, declare herewith that the present thesis is exclusively my own work, based on my research and only such external information as properly credited in notes and bibliography. I declare that no unidentified and illegitimate use was made of the work of others, and no part of the thesis infringes on any person’s or institution’s copyright. -

Croatia's Cities
National Development Strategy Croatia 2030 Policy Note: Croatia’s Cities: Boosting the Sustainable Urban Development Through Smart Solutions August 2019 Contents 1 Smart Cities – challenges and opportunities at European and global level .......................................... 3 1.1 Challenges .................................................................................................................................. 4 1.2 Opportunities .............................................................................................................................. 5 1.3 Best practices ............................................................................................................................. 6 2 Development challenges and opportunities of Croatian cities based on their territorial capital .......... 7 3 Key areas of intervention and performance indicators ....................................................................... 23 3.1 Key areas of intervention (KAI)............................................................................................... 23 3.2 Key performance indicators (KPI) ........................................................................................... 24 4 Policy mix recommendations ............................................................................................................. 27 4.1 Short-term policy recommendations (1-3 years) ...................................................................... 27 4.2 Medium-term policy recommendations (4-7 years) ................................................................ -

Neolithisation of Sava-Drava-Danube Interfluve at the End of the 6600–6000 BC Period of Rapid Climate Change> a New Solutio
Documenta Praehistorica XLIII (2016) Neolithisation of Sava-Drava-Danube interfluve at the end of the 6600–6000 BC period of Rapid Climate Change> a new solution to an old problem Katarina Botic´ Institute of Archaeology, Zagreb, CR [email protected] ABSTRACT – The idea of the Neolithisation of the Sava-Drava-Danube interfluve has undergone very little change since S. Dimitrijevi≤'s time. Despite their many shortcomings, new archaeological exca- vations and radiocarbon dates of Early Neolithic sites have provided us with new insight into the process of Neolihisation of this region. Using the recently published work by B. Weninger and L. Clare (Clare, Weninger 2010; Weninger et al. 2009; Weninger et al. 2014) as a starting point, the available radiocarbon and archaeological data are used to build up a time frame comparable to the wider region of Southeast Europe and climate conditions for specific period. The results fit the model of Neolithisation well (Weninger et al. 2014.9, Fig. 4), filling in the geographical gaps. IZVLE∞EK – Premise o neolitizaciji v medre≠ju Save, Drave in Donave se od ≠asa S. Dimitrijevi≤a niso veliko spremenile. Nova arheolo∏ka izkopavanja in radiokarbonski datumi zgodnjega neolitika so, kljub mnogim pomanjkljivostim, prinesli nove vpoglede v proces neolitizacije na tem obmo≠ju. Za os- novo pri interpretaciji smo uporabili nedavno objavljena dela B. Weningerja in L. Clarea (Clare, We- ninger 2010; Weninger et al. 2009; Weninger et al. 2014), dosegljive radiokarbonske datume in arheo- lo∏ke podatke pa smo uporabili za izdelavo ≠asovnega okvirja, ki je primerljiv s ∏ir∏im obmo≠jem ju- govzhodne Evrope in s klimatskimi pogoji za posamezna obdobja. -

Embassy of India Zagreb *** India - Croatia Relations
Embassy of India Zagreb *** India - Croatia Relations Political Relations Relations between India and Croatia have been friendly since the days of the former Yugoslavia (SFRY). Marshal Tito, a Croat, who ruled Yugoslavia for more than three decades, maintained close relations with the then Indian leadership. Nehru and Tito were also pioneers of NAM. Croatia dominated bilateral trade relations accounting for more than two-thirds of trade between India and the former Yugoslavia. This included large scale purchases of Croatian ships by India in the 1970s and 1980s. India recognized Croatia in May 1992 and established diplomatic relations MOS (IC) / C&I, N.Sitharaman in Croatia on 9 July 1992. Croatia opened its resident (14-15 Feb 2017) mission at New Delhi in February 1995. The Indian Mission in Zagreb was opened on 28 April 1996, and upgraded to Ambassadorial level in January 1998. Bilateral relations have remained friendly at the political level but the economic ties have lagged since the Tito era, and the effort is to provide resurgence to this aspect of the relationship. There is good cooperation between the two countries at the multilateral level. VVIP Visits: (a) From Croatia: Former Croatian President Stjepan Mesić paid a State Visit to India, 12-16 November 2002. In the Joint Statement, Croatia expressed support for India’s claim for permanent membership of the UNSC. (b) From India: Vice-President M. Hamid Ansari visited Croatia, 9-11 June 2010 at the invitation of Croatian President Ivo Josipovic. Ministerial Level Visits: (a) From Croatia: 1. Dr. Zvonimir Separović, Foreign Minister (April 1992). -

Vina Croatia
Wines of CROATIA unique and exciting Croatia as a AUSTRIA modern country HUNGARY SLOVENIA CROATIA Croatia, having been eager to experience immediate changes, success and recognition, has, at the beginning of a new decade, totally altered its approach to life and business. A strong desire to earn quick money as well as rapid trade expansion have been replaced by more moderate, longer-term investment projects in the areas of viticulture, rural tourism, family hotels, fisheries, olive growing, ecological agriculture and superior restaurants. BOSNIA & The strong first impression of international brands has been replaced by turning to traditional HERZEGOVINA products, having their origins in a deep historic heritage. The expansion of fast-food chains was brought to a halt in the mid-1990’s as multinational companies understood that investment would not be returned as quickly as had been planned. More ambitious restaurants transformed into centres of hedonism, whereas small, thematic ones offering several fresh and well-prepared dishes are visited every day. Tradition and a return to nature are now popular ITALY Viticulture has been fully developed. Having superior technology at their disposal, a new generation of well-educated winemakers show firm personal convictions and aims with clear goals. The rapid growth of international wine varietals has been hindered while local varietals that were almost on the verge of extinction, have gradually gained in importance. Not only have the most prominent European regions shared their experience, but the world’s renowned wine experts have offered their consulting services. Biodynamic movement has been very brisk with every wine region bursting with life. -

Obstacles to Cross-Border Cooperation – Case of Croatia and Hungary
European Journal of Geography Volume 9, Number 2: 116-133, June 2018 ©Association of European Geographers OBSTACLES TO CROSS-BORDER COOPERATION – CASE OF CROATIA AND HUNGARY Sanja TIŠMA Institute for Development and International Relations, IRMO, Zagreb, Croatia [email protected] Krešimir JURLIN Institute for Development and International Relations, IRMO, Zagreb, Croatia [email protected] Helena ČERMAK Institute for Development and International Relations, IRMO, Zagreb, Croatia [email protected] Abstract The focus of this paper is to identify most significant obstacles that hinder bilateral trade between Hungary and Croatia and propose solutions for improvements by using the gravity models, precisely the Newtonian model of gravitation. The results of the research show that in spite of interest for cross-border cooperation being expressed by the stakeholders from both sides of the border, Somogy County and Virovitica-Podravina County belong to less developed, deprived rural areas of Hungary and Croatia. The key weaknesses for cross-border cooperation include lack of transport connections and language barrier, while strengths reflect in entrepreneurial spirit and opportunity to apply and implement joint entrepreneurial projects financed by the European Union (EU) funds. Keywords: Cross-border cooperation, Croatia and Hungary, gravity models, entrepreneurship, transport infrastructure, EU funds 1. INTRODUCTION When considering bilateral trade, often the crucial question is what trade intensity shall be considered as appropriate or "normal". It has been known since the work of Tinbergen (1962) and Poyhonen (1963) that the size of bilateral trade flows between any two countries can be approximated by a law called the gravity equation which originates from the Newtonian theory of gravitation. -
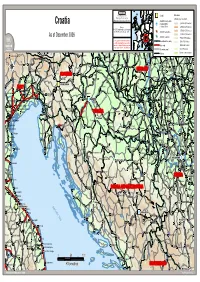
Croatia Atlas
FF II CC SS SS Field Information and Capital Elevation Coordination Support Section (Above mean sea level) Division of Operational Services UNHCR Country Office Croatia / National Office 3,250 to 4,000 metres Sources: / Liaison Office 2,500 to 3,250 metres UNHCR, Global Insight digital mapping 1,750 to 2,500 metres © 1998 Europa Technologies Ltd. UNHCR Field Office As of December 2009 1,000 to 1,750 metres UNHCR Field Unit 750 to 1,000 metres The boundaries and names shown International boundary 500 to 750 metres and the designations used on this map do not imply official endorsement Main road 250 to 500 metres or acceptance by the United Nations. Secondary road 0 to 250 metres g Name_of_the_workspace.WOR !! Villach !! !! !! !! Below mean sea level !! !! Davograd Railway !! Marcali !! Orosháza !! Maribor !! Szank !! !! Cortina d'Ampezzo !! !! !! Mursko Sredisce !! Kalocsa!! Kecel !! Mindszent !! !! !! Kiskunmajsa !! !! Nagykanizsa !! Jesenice Tolna !! Kiskunhalas !! !! Ptuj !! !! Hajós !! !! Hódmezövásárhely!! !! !! !! Tolmezzo !! Böhönye !! !! !! !! !! !! Cakovec !! !! Sostanj !! !! !! Forraaskut !! !! Kaposvár !! !! Balotaszállás!! !! !! !! !! Mezöhe !! Varazdin HUNGARY!! !! Jánoshalma !! !! !! !! !! !! !! !! !! Legrad !! !! Ruzsa !! !! !! !! !! !! !! !! !! !! !! !! !! !! !! Gemona del Friuli !! !! !! !! !! !! !! !! Csurgó !! !! Szeged !! Kranj !! Celje !! Nagyatád !! !! !! Ivanec !! !! SLOVENIA !! !! !! Makó !! Durmanec !! Komló !! Maniago !! !! !! !! !! !! !! Koprivnica !! Baja !! Horgos !! Nadlac ! !! Belluno !! -

Egypt in Croatia Croatian Fascination with Ancient Egypt from Antiquity to Modern Times
Egypt in Croatia Croatian fascination with ancient Egypt from antiquity to modern times Mladen Tomorad, Sanda Kočevar, Zorana Jurić Šabić, Sabina Kaštelančić, Marina Kovač, Marina Bagarić, Vanja Brdar Mustapić and Vesna Lovrić Plantić edited by Mladen Tomorad Archaeopress Egyptology 24 Archaeopress Publishing Ltd Summertown Pavilion 18-24 Middle Way Summertown Oxford OX2 7LG www.archaeopress.com ISBN 978-1-78969-339-3 ISBN 978-1-78969-340-9 (e-Pdf) © Authors and Archaeopress 2019 Cover: Black granite sphinx. In situ, peristyle of Diocletian’s Palace, Split. © Mladen Tomorad. All rights reserved. No part of this book may be reproduced, or transmitted, in any form or by any means, electronic, mechanical, photocopying or otherwise, without the prior written permission of the copyright owners. Printed in England by Severn, Gloucester This book is available direct from Archaeopress or from our website www.archaeopress.com Contents Preface ���������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������xiii Chapter I: Ancient Egyptian Culture in Croatia in Antiquity Early Penetration of Ancient Egyptian Artefacts and Aegyptiaca (7th–1st Centuries BCE) ..................................1 Mladen Tomorad Diffusion of Ancient Egyptian Cults in Istria and Illyricum (Late 1st – 4th Centuries BCE) ................................15 Mladen Tomorad Possible Sanctuaries of Isaic Cults in Croatia ...................................................................................................................26