The Hamiltonian Property of Generalized De Bruijn Digraphs
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Alphabets, Letters and Diacritics in European Languages (As They Appear in Geography)
1 Vigleik Leira (Norway): [email protected] Alphabets, Letters and Diacritics in European Languages (as they appear in Geography) To the best of my knowledge English seems to be the only language which makes use of a "clean" Latin alphabet, i.d. there is no use of diacritics or special letters of any kind. All the other languages based on Latin letters employ, to a larger or lesser degree, some diacritics and/or some special letters. The survey below is purely literal. It has nothing to say on the pronunciation of the different letters. Information on the phonetic/phonemic values of the graphic entities must be sought elsewhere, in language specific descriptions. The 26 letters a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z may be considered the standard European alphabet. In this article the word diacritic is used with this meaning: any sign placed above, through or below a standard letter (among the 26 given above); disregarding the cases where the resulting letter (e.g. å in Norwegian) is considered an ordinary letter in the alphabet of the language where it is used. Albanian The alphabet (36 letters): a, b, c, ç, d, dh, e, ë, f, g, gj, h, i, j, k, l, ll, m, n, nj, o, p, q, r, rr, s, sh, t, th, u, v, x, xh, y, z, zh. Missing standard letter: w. Letters with diacritics: ç, ë. Sequences treated as one letter: dh, gj, ll, rr, sh, th, xh, zh. -

Recharge NY (RNY) Description
ReCharge New York A New York Power Authority Program As of April 2016 2 Overview NYPA and ReCharge NY (RNY) Description Application and Contract Process Evaluation Criteria Statistics 3 ReCharge NY (RNY) Program Description 4 NYPA/ReCharge NY (RNY) o NYPA is the largest state public power organization in the U.S. o Owns and operates 16 power plants o Operates 1,400 circuit-miles of the NYS transmission system o RNY is Governor Cuomo’s statewide economic development electric power program o 910 Megawatts (MW) o 50% NYPA hydropower o 50% market power procured by NYPA o Focuses on job creation or retention for existing, expanding, or new businesses 5 ReCharge NY (RNY) Program Description o Minimum of 350 MW for applicants within NYSEG, National Grid, and RG&E territories o All NYS utility customers can participate in RNY o Minimum 200 MW for attracting new businesses to New York State and expanding existing businesses o 100 MW for small businesses and not-for-profits 6 Eligibility Criteria • Large businesses (above 400 kW peak demand) • Small businesses (equal or less than 400 kW peak demand) Who’s • A corporation defined in Section 102 of the state’s Not-For-Profit Corporation Eligible? Law, subdivision five of paragraph (a) • Retail businesses • Sports venues Who’s not • Gaming or entertainment related establishments Eligible? • Places of overnight accommodations 7 Application & Contract Process 8 RNY Application Process Applicants must apply online through the Consolidated Funding Application (CFA): o The CFA is a single application for multiple funding sources o To access the CFA, please visit http://regionalcouncils.ny.gov Regional Economic Development Councils: o Developed strategic plans o Provide input on RNY applications to determine consistency with strategies and priorities for their respective regions 9 Application Review o Regional Councils: Score each application, contributing to 20% of the applicants’ overall score. -
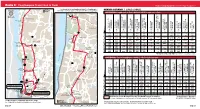
Dutchess County Public Transit Route C
Route C: Poughkeepsie Transit Hub to Tivoli Please see map on page 24 / Favor ver el mapa en la página 24 See map at left for continuation of Route C to Poughkeepsie / To/From MONDAY–SATURDAY / LUNES–SABADO NORTH / NORTE Ver el mapa a la derecha para la continuación de la Ruta C a Poughkeepsie Tivoli N Cross Rd NORTHBOUND: Poughkeepsie to Tivoli / HACIA EL NORTE: Poughkeepsie a Tivoli Tivoli Free Old Post Rd Library 13 Pine St Map not to scale 15 Broadway Mapa no a escala Tivoli Village of 14 Staatsburg Tivoli Hall W Anderson Center K erl S Cross Rd ey for Autism C or Kidd Ln n er s Rd Route 9 & CR 41 St) (East Market PARK HYDE Budds C Red Hook County Dutchess Hub Transit POUGHKEEPSIE Poughkeepsie StationTrain POUGHKEEPSIE Fulton St E & Beck Pl College Marist POUGHKEEPSIE DCC Lot E Bus Shelter POUGHKEEPSIE Ln Dorsey West & Route 9 (CIA) PARK HYDE Route 9 S (Across from Stop & Shop) PARK HYDE Stop Shop & PARK HYDE Route 9G (Violet & Ave) East Market St CR 41) PARK HYDE Stop Shop & RHINEBECK Route & 199 9G Route HOOK RED Bard College (Kline Bus Stop) HOOK RED Pine St & Katherine Ln TIVOLI orners Rd Stop # 1 2 3 4 5 6 7 8 9 10 11 12 13 1 3 117 89 93 88 94 116 80 104 96 81 100 Cruger Island Rd 9G Albany Post Rd 5:35 5:40 — — 5:47 5:50 * — — 6:16 6:27 * 6:39 6:05 6:10 — — 6:17 6:20 * — — 6:46 6:57 — 7:09 9G 12 W halesback R d 7:30 7:35 — 7:46 — — — 8:04 8:07 8:20 — — — Bard AM 8:30 8:35 — 8:46 8:54 8:57 8:58 — — 9:20 9:31 9:36 9:43 College 9:15 9:20 — 9:31 9:39 9:42 9:43 — — 10:08 10:19 10:24 10:30 Town of Hyde Hyde Park 11:00 11:05 — 11:16 -

Reminiscences of Red Hook" in November, 1926
Reminiscences of Red Hook (A story of the Village) by Edmund Bassett Edmund Bassett was born in Red Hook about 1865. He studied telegraphy and held various positions with the New York Central Railroad, among them Stationmaster at Tivoli. Later in life he went to New York City where he was very successful. Like most people who move to a big city life in a small town is remembered with great fondness. Mr. Bassett was no exception and these reminiscences were an expression of his feeling. Mr. Bassett started his "Reminiscences of Red Hook" in November, 1926. These were published weekly over a period of three months in the REV HOOK AVVERTISER. The second series, "Reminisoenoes of Some of the Highways and Byways of Red Hook" were written in 1928 and published in the REV HOOK AVVERTISER over a period of several months from April 10, 1930 to October 9, 1930. By using the enclosed 1867 map of the Village of Red Hook, it is possible to follow Mr. Bassett's travels.and identify families, buildings, and streets mentioned in the articles. Reprinted June 1976 by Red Hook-Tivoli Bicentennial Committee REMINISCENCES OF RED HOOK By Edmund Bassett As good "Americans" we should love our native country, but no part of same is so dear to me as Red Hook, the spot where I first saw the light of day. We should all follow the commandment, "Love your neighbor as yourself" and all men are our neighbors; but the poor and down trodden should ever have a special appeal to us, and they do; but the old neighbors at home, in dear old Red Hook, have an appeal all their own to me. -

New York Standards Alignment ELA: Kindergarten Through Grade 3
New York Standards Alignment 2011 New York State P-12 Common Core Learning Standards, produced by the State Department of Education ELA: Kindergarten through Grade 3 English Language Arts and Literacy in History/Social Studies Math: Prekindergarten through Grade 1 Trademark of Renaissance Learning, Inc., and its subsidiaries, registered, common law, or pending registration in the United States and other countries . P.O. Box 8036 • Wisconsin Rapids, WI 54495-8036 Phone: (800) 338-4204 • Fax: (715) 424-4242 www.renlearn.com New York Standards Alignment Standards List with Aligned Product Skills The Standards List with Aligned Product Skills Report is a standards-oriented document showing the entire list of standards for the subject, discipline, and grade and the product skills aligned to those standards. This alignment report shows the breadth of standards coverage for the purpose and focus of this product. Note to Educator ................................................................................................... iii ELA: Kindergarten English Language Arts and Literacy in History/Social Studies ........................... 1 ELA: Grade 1 English Language Arts and Literacy in History/Social Studies ................................ 5 ELA: Grade 2 English Language Arts and Literacy in History/Social Studies ................................ 9 ELA: Grade 3 English Language Arts and Literacy in History/Social Studies ................................ 12 Math: Prekindergarten ............................................................................................. -

Interim Guidance for Office-Based Work During the Covid-19 Public Health Emergency
INTERIM GUIDANCE FOR OFFICE-BASED WORK DURING THE COVID-19 PUBLIC HEALTH EMERGENCY When you have read this document, you can affirm at the bottom. As of June 8, 2021 Purpose This Interim Guidance for Office-Based Work during the COVID-19 Public Health Emergency (“Interim COVID-19 Guidance for Office-Based Work”) was created to provide businesses and entities that operate in office spaces and their employees and contractors with precautions to help protect against the spread of COVID-19 as their businesses reopen or continue to operate. This guidance addresses business activities where the core function takes place within an office setting. This guidance may apply – but is not limited – to businesses and entities in the following sectors: Professional services, nonprofit, technology, administrative support, and higher education administration (excluding full campus reopening). Please note that these guidelines may also apply to business operating parts of their business functions under different guidelines (e.g. front office for a construction company). This guidance does not address medical offices, such as doctors’ offices or dentists’ offices. This guidance also does not address building owners/managers and their employees or contractors. For more information on building management, see, “Interim COVID-19 Guidance for Commercial Building Management.” Owners and operators of offices are authorized to require masks and six feet of social distancing for employees within their establishments or adhere to DOH guidance, consistent with the Centers for Disease Control and Prevention’s (CDC) “Interim Public Health Recommendations for Fully Vaccinated People.” If choosing to adhere to CDC guidance, offices generally do not congregate patrons or operate above the State’s social gathering limits, and must follow applicable guidelines for masks, distancing, and capacity as outlined in New York State’s guidelines on Implementing CDC Guidance. -

Multiple Feature Affixation in Seenku Plural Formation
Pre-publication version, please use caution in citing, to appear in Morphology (journal) Multiple feature affixation in Seenku plural formation Laura McPherson (Dartmouth College) Abstract Nominal plural formation in Seenku involves two surface changes: fronting of the final vowel and raising of the final tone. Diachronically, the plural patterns likely derive from a suffix *-˝ı, which has been obscured through the loss of falling sonority diphthongs. By comparing plural formation to other morphophonological processes in Seenku, this paper argues that the plural suffix has been restructured as a featural suffix consisting of two features: the vocalic feature [+front], resulting in vowel fronting, and the tonal feature [+raised], resulting in tone raising. Given the atomic nature of the morphosyntactic feature plural, Seenku plural formation represents a strong case of multiple feature affixation, albeit a case that can be ac- counted for through Max constraints on feature values (Lombardi 1998, 2001, etc.) and Realize-Morpheme (van Oostendorp 2005, Trommer 2012) rather than the constraint Max-Flt argued for by Wolf (2007). A level-ordered approach retaining the vocalic suffix is also considered but is shown to suffer from a number of short- comings, particularly with respect to tone and a challenging class of nasal stems. In short, this paper explores how the synchronic grammar copes with the vestiges of affixal morphology in a language that has undergone heavy reduction. 1 Introduction Seenku (ISO 639-3 [sos], exonym Sambla or Sembla) is a Northwestern Mande language of Burkina Faso with very little apparent affixation. The majority of morphosyntactic meanings are conveyed either analytically or through what appear to be patterns of base modification. -

Instructions for Form IT-201 Full-Year Resident Income Tax Return
Department of Taxation and Finance IT-201-I Instructions Instructions for Form IT-201 Full-Year Resident Income Tax Return New York State • New York City • Yonkers • MCTMT (including instructions for Forms IT-195 and IT-201-ATT) Before you prepare a paper return, consider filing electronically • Electronic preparation and filing is fast, easy, and secure. • Electronic filers get their refunds up to twice as fast as paper filers. • The user-friendly software ensures you file all the right forms and don’t miss out on valuable credits. Visit www.tax.ny.gov to file and learn more. If you do file a paper return, you may need these additional forms, as well as credit claim forms. Use Form: to: IT-2 report wages and NYS, NYC, or Yonkers tax withheld (do not submit Form W-2). IT-195 allocate all or a portion of your personal income tax refund to a NYS 529 account. IT-196 claim the New York itemized deduction IT-201-V make a payment by check or money order with your return. IT-1099-R report NYS, NYC, or Yonkers tax withheld from annuities, pensions, retirement pay, or IRA payments (do not submit Form 1099-R). IT-201-ATT report other NYS or NYC taxes or to claim credits other than those reported on Form IT-201. IT-225 report NY addition and subtraction modifications not reported directly on Form IT-201. IT-227 make voluntary contributions IT-558 report addition and subtraction adjustments to federal amounts due to decoupling from the IRC. Reminder: To claim a tax credit (with the exception of the household credit and NYC school tax credit) you must complete and submit the appropriate credit form. -

MUFI Character Recommendation V. 3.0: Code Chart Order
MUFI character recommendation Characters in the official Unicode Standard and in the Private Use Area for Medieval texts written in the Latin alphabet ⁋ ※ ð ƿ ᵹ ᴆ ※ ¶ ※ Part 2: Code chart order ※ Version 3.0 (5 July 2009) ※ Compliant with the Unicode Standard version 5.1 ____________________________________________________________________________________________________________________ ※ Medieval Unicode Font Initiative (MUFI) ※ www.mufi.info ISBN 978-82-8088-403-9 MUFI character recommendation ※ Part 2: code chart order version 3.0 p. 2 / 245 Editor Odd Einar Haugen, University of Bergen, Norway. Background Version 1.0 of the MUFI recommendation was published electronically and in hard copy on 8 December 2003. It was the result of an almost two-year-long electronic discussion within the Medieval Unicode Font Initiative (http://www.mufi.info), which was established in July 2001 at the International Medi- eval Congress in Leeds. Version 1.0 contained a total of 828 characters, of which 473 characters were selected from various charts in the official part of the Unicode Standard and 355 were located in the Private Use Area. Version 1.0 of the recommendation is compliant with the Unicode Standard version 4.0. Version 2.0 is a major update, published electronically on 22 December 2006. It contains a few corrections of misprints in version 1.0 and 516 additional char- acters (of which 123 are from charts in the official part of the Unicode Standard and 393 are additions to the Private Use Area). There are also 18 characters which have been decommissioned from the Private Use Area due to the fact that they have been included in later versions of the Unicode Standard (and, in one case, because a character has been withdrawn). -

Phonics Progress Monitoring: Sound-Spellings Word Recognition Assessments
z y L x I r K H a g G Q F p w f J E Q o P D B C A n e v P I m O l i j k d c Y N Ssd e f g h u O c X H M t L OE J K b b G H I N s W a z G gp q r y M r G s t x Ff u v w L a V q q F K Y Z A B J C I p z p D E H E U F G o f d e gd e n D y o c f m T g h i j k l b M a C x S S n U V B T W r S X Y Z A L R R w R v Unit 2 o p m o n q r t u K s Q l O m J l J K P k I L M N O k H j I K i Assessment and Remediation Guide G b c d h a e f g H a DStrand Skills • Edition York New • B C F G Core Knowledge Language Arts® Arts® Language DKnowledge Core E A 1 Grade A Unit 2 Assessment and Remediation Guide Skills Strand Grade 1 Core Knowledge Language Arts® New York Edition Creative Commons Licensing This work is licensed under a Creative Commons Attribution- NonCommercial-ShareAlike 3.0 Unported License. You are free: to Share — to copy, distribute and transmit the work to Remix — to adapt the work Under the following conditions: Attribution — You must attribute the work in the following manner: This work is based on an original work of the Core Knowledge® Foundation made available through licensing under a Creative Commons Attribution- NonCommercial-ShareAlike 3.0 Unported License. -

Design and Positioning of Diacritical Marks in Latin Typefaces Authors
Turčić et al.: Design and Positioning of Diacritical..., acta graphica 22(2010)3-4, 5-15 udc 655.244 original scientific paper received: 07-12-2010 acta graphica 185 accepted: 23-02-2011 Design and Positioning of Diacritical Marks in Latin Typefaces Authors Maja Turčić1*, Antun Koren2, Vesna Uglješić1, Ivan Rajković1 1Polytechnic of Zagreb 2Faculty of Graphic Arts, Croatia University of Zagreb, Croatia *E-mail: [email protected] Abstract: This paper presents relevant information concerning the types, shape and posi- tioning of diacritical marks in Latin typefaces. The aim is to increase the aware- ness of the importance of diacritics, their design and use. The design of the low- ercase dcroat letter presents a particular problem, because it is present only in the Croatian and Vietnamese script and is therefore often incorrectly designed or it is missing the respective font. Data on the most common methods of shaping and positioning of this diacritical sign was collected by measuring the geometry of the dcroat letter in various fonts. Most common designers’ mistakes were shown and evaluated. Suggestions for the design of diacritical marks are proposed taking into account asymmetry, width, uppercase, vertical and horizontal positioning and cul- tural preferences. Keywords: Diacritical Mark, Typography, Character Design 1. Introduction characters in a particular language. Diacritics are signs that change the meaning or the pro- Despite a large number of fonts, available nunciation of certain letters, and without them, technology (both software and hardware), and correct grammar and written communication technical capabilities in the form of coding come into question. systems, there are many fonts that lack certain characters, thus disturbing proper written com- When designing diacritics one should be munication of non-Western Latin script users. -

On the Creation of a Pronunciation Dictionary for Hungarian
On the creation of a pronunciation dictionary for Hungarian Stephen M. Grimes [email protected] August 2007 Abstract This report describes the process of creating a pronunciation dictionary and phonological lexicon for Hungarian for the purpose of aiding in linguistic research on Hungarian phonology and phonotactics. The pronunciation dictionary was created by transforming orthographic forms to pronunciation representations by taking advantage of systematic deviations between Hungarian orthography and pronunciation. It is argued that the “automated” creation of such a dictionary is reasonably expected to be accurate due to the relative similarity of Hungarian orthography to actual pronunciation. This document includes discussion of goals and standards for creating a Hungarian pronunciation dictionary, and each phonological change creating a mismatch between orthography and pronunciation is highlighted. Future developments and additions to the current dictionary are also suggested as well as strategies for evaluating the quality of the dictionary. Finally, potential applications to linguistic research are discussed. 1 Introduction While students of the English language quickly learn that English spelling is by no means consistent, many Hungarians believe that the Hungarian alphabet is completely phonetic. Here, a phonetic alphabet refers to the existence of a one-to-one mapping between symbol and sound. It can quite easily be demonstrated by counter-example that 1 Hungarian orthography is not phonetic, and in fact several types of orthographic- pronunciation discrepancies exist. Consider as an example the word /szabadság/ 1 [sabatʃ:a:g] ‘freedom, liberty’ , in which no fewer than four orthographic-pronunciation discrepancies can be identified with the written form of this word: (1) a.