DOCSLIB.ORG

Real World Performance Tasks

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Real World Performance Tasks Cedar Point Real World Performance Tasks Real World Real Life, Real Data, Real-Time - These activities put students into real life scenarios where they use real-time, real data to solve proBlems. In the Relationship Status series, we use data from theme parks and update our data regularly. Note - some data has been rounded or simplified in order to adjust the math to the appropriate level. Engaging Relevant – Students today are familiar with and enjoy amusement park rides, making these activities very relevant to children’s everyday lives. To pique their interest further, try asking the Your Challenge question to the class first. Authentic Tasks - Through these activity sheets students learn how the amusement park industry works and are prompted to form opinions and ideas about how they would solve real life proBlems. A glossary is included to help them with the unfamiliar terms used. Student Choice - Each set of activity sheets is available in multiple versions where students will do the same activities using data for different amusement parks (e.g., Busch Gardens, Hershey Park, Six Flags, etc.) You or your students can pick the location that most interests them. Modular Principal Activity - The activity sheets always start with repeated practice of a core skill matched to a common core standard, as set out in the Teacher Guide. This principal activity (or Level 1 as it is labeled to students) can Be used in isolation. This should generally take around 10-15 minutes. Step Up Activity - For the Level 2 questions, students are required to integrate a different skill or set of skills with increasing complexity. The additional skills used to answer these questions are set out in the Teacher Guide. This should generally take around 20-30 minutes. Challenge - This is designed to require critical thinking skills and stretch students to reason with math and data to come to conclusions. They are matched up with one of the Common Core Standards for Mathematical Practice. These activities work well with students in pairs or small groups where they can discuss the math. Cross-Curricular Activity - Every activity sheet also includes a finale that you can use to extend the math lesson into another suBject (usually ELA). These could Be assigned in a second lesson or for homework. Customizable All of the activity sheets are provided in Word so that they can Be differentiated to add remove or edit questions or even add space for students to show their work. Suggested customizations for each activity sheet are given in the Teacher Guide. Community We would love you and your students to tell us about your experience. Join the conversation on Twitter starting your tweet with @nextlesson and using #Coasters. Updated July 2014 © NextLesson 2014 Scatter Plots Teacher Guide Sound bite for Students: “In the real world, we use graphs to model relationships between quantities so that it is easier to investigate patterns and interpret the data.” Skills Practiced: Principal Activity (Level 1): - Construct and interpret scatter plots Step Up Activity (Level 2): - Draw and interpret a line of Best fit Common Core Math Standards Addressed: Construct and interpret scatter plots for Bivariate measurement data to Principal investigate patterns of association Between two quantities. DescriBe patterns 8.SP.A.1 Activity: such as clustering, outliers, positive or negative association, linear association, and nonlinear association. Know that straight lines are widely used to model relationships Between two quantitative variables. For scatter plots that suggest a linear association, 8.SP.A.2 Step Up informally fit a straight line, and informally assess the model fit By judging the Activity: closeness of the data points to the line. Use the equation of a linear model to solve proBlems in the context of 8.SP.A.3 Bivariate measurement data, interpreting the slope and intercept. Differentiation Tips: You can edit any of the activity sheets to: - change the numbers or tasks given (e.g. construct one scatter plot in L1 for the students and ask them to simply interpret it) - add or remove hints for differentiation purposes (e.g. provide a scale for the plots in L1, include terminology for students to use when describing the associations in L1) - remove/add questions (e.g. eliminate the data in L2 relating to inversions) - encourage students to create scatter plots in Excel or use graphing calculators Due to school paper restriction, the spacing provided is only for answers. However, you could modify the spacing to add room for work if desired. Updates: At NextLesson we strive to engage students with data that is real and real-time. This lesson uses data as of July 2014. Please come Back for the most recent updates. Updated July 2014 © NextLesson 2014 Cedar Point Name: ________________________________ You are an engineer working for a company that designs rides for amusement parks. You are investigating the construction of various attractions at Cedar Point. Your Challenge: How do the thrill features of a ride’s construction influence the design process? LEVEL 1 You decide to begin your investigation with two of the features that thrill riders often seek. 1. Construct a scatter plot that shows the relationship between the maximum speed and the drop height. Max. Drop Attraction Speed Height (mph) (feet) Millennium Force 93 299 Maverick 70 328 Wicked Twister 72 206 Magnum XL-200 72 639 Disaster Transport 40 50 2. Interpret the scatter plot. a. What tends to happen as the maximum speed increases? b. Describe the association between the two quantities. c. Identify any outliers, gaps, or clusters. 1 Updated June 2014 © NextLesson 2014 Cedar Point Next, you examine two of the features that are considered at the start of any design project: length and duration of the ride. 3. Construct a scatter plot that shows the relationship between the track length and the duration of the ride. Length Attraction Duration (feet) Millennium Force 6,595 02:20 Maverick 4,450 02:30 Wicked Twister 675 00:40 Magnum XL-200 5,106 02:00 Disaster Transport 1,932 02:32 4. Interpret the scatter plot. a. Describe the association between the two quantities. b. How does this relationship compare to the relationship between speed and height? c. Identify any outliers, gaps, or clusters. 2 Updated July 2014 © NextLesson 2014 Cedar Point LEVEL 2 Now that you have found relationships between some of the design features, you want to make predictions to help the design team make decisions about new construction. You know a line of best fit can be used to estimate and predict and you decide to draw one on a graph and write an equation to calculate the best fit. 5. Draw a line of best fit in the scatter plot that shows the relationship between the maximum speed and the drop height. a. Write an equation of the line of best fit. b. Interpret the slope of the line of best fit. c. Predict the maximum speed with a drop height of 50 feet. d. Estimate the drop height needed for a maximum speed of 100 miles per hour. 6. Draw a line of best fit in the scatter plot that shows the relationship between the track length and the duration of the ride. a. Is it possible to draw a line of fit for the data? If so, write an equation of the line of fit and interpret the slope. b. Is it reasonable to use the scatter plot to predict the duration of a ride based on the length of the track? Explain. 7. You have also gathered data on the number of inversions each ride has. Relate this data to the other variables. Do you expect to find any correlations? Attraction Inversions Millennium Force 0 Maverick 2 Wicked Twister 0 Magnum XL-200 0 Disaster Transport 0 3 Updated July 2014 © NextLesson 2014 Cedar Point Challenge Before presenting your findings to the park’s management team, you decide to expand your investigation to include attractions from another park, Busch Gardens Tampa Bay. Max Speed Drop Height Length Attraction Duration Inversions (mph) (feet) (feet) Cheetah Hunt 60 130 4,429 3:30 1 Gwazi 51 92 3,508 2:30 0 Kumba 60 135 3,978 2:54 7 Montu 60 128 3,983 3:00 7 Sand Serpent 28 46 1,214 1:50 0 Scorpion 41 45 1,818 1:30 1 1. Revise your scatter plots to include the data from the attractions at both theme parks. Use another color to represent the Busch Gardens Tampa Bay. What do you notice? 2. Use a graphing calculator to find the line of best fit for each scatter plot. a. Differentiate between your equation of the line of fit and the calculator’s line of best fit. b. Identify and interpret the correlation coefficient. 3. Explain the difference between estimating the line of best fit with more data points rather than with fewer data points. 4. Synthesize your findings to explain how different features of a ride’s construction may influence the design process. Think about their relationships with each other and how they influence each other. 4 Updated July 2014 © NextLesson 2014 Cedar Point Finale You could give students one of the following ideas or have them choose themselves. 1. Create a presentation to give to your design team to share your findings on how different features of a ride’s construction may influence the design process. Be sure to use the data trends to cite evidence as support. 2. Safety is a major concern for the engineering design team. Create an infographic to suggest appropriate maximum speeds to consider in relation to other features for a new ride you are designing.
Load more

Recommended publications
  • Golden Ticket Awards • September 16 & 17, 2011 COURTESY S
    GOLDEN TICKET BONUS ISSUE TM www.GoldenTicketAwards.com Vol. 15 • Issue 6.2 SEPTEMBER 2011 Holiday World hosts Golden Ticket event for third time Amusement Today sees the biggest voter response in survey history 2011 . P . I GOLDEN TICKET . V AWARDS BEST OF THE BEST! Holiday World & Splashin’ Safari Host Park • 2011 Golden Ticket Awards • September 16 & 17, 2011 COURTESY S. MADONNA HORCHER STORY: Tim Baldwin strate the big influx of additional voters. [email protected] Tabulating hundreds of ballots can seem SANTA CLAUS, Indiana — It was Holiday like a somewhat tedious and daunting task, World’s idea for Amusement Today to pres- but a few categories were such close races, ent the Golden Ticket Awards live in 2000. that a handful of winners were not determined The ceremony was on the simple side, and until the very last ballots in the last hour of now over a decade later, the park welcomes tabulation. These ‘nail biters’ always keep us AT for the third time. A lot has changed since on our toes that there is never a guarantee of that time, as the Golden Ticket Awards cere- any category. mony has grown into a popular industry event, The dedication of our voters is also admi- filled with networking opportunities and occa- rable. People have often gone to great lengths sions to see what is considered the best in the to make sure we receive their ballot in time. industry. And as mentioned before, every vote abso- What has also grown is the voter response. lutely counts as just a few ballots determined The 2011 awards saw the biggest response some winning categories.
    [Show full text]
  • 2020 High School Workbook
    Schedule of Events TIME EVENT LOCATION 8:45 Lagoon Autopark (parking lot) opens 9:30 Lagoon Main Gates to rides opens Main Gate 9:00 - 11:00 School & teacher registration Main Gate Main Gate 9:30 - 11:00 Contest registration & safety approval inspections Davis Pavilion 10:00-11:00 Utah/Idaho FIRST Robotics Grudge Match—Semifinals 10:00-2:00 Mindstorm Activities Maple Terrace 10:00-2:00 MESA Arduino Clean Air Solutions and Mouse Trap Car Oak Terrace 12:00 - 1:00 Faculty and staff complimentary lunch Canyon Terrace High School Student Workbook 2:30 - 3:30 Contest winners are posted as judging is completed Davis Pavilion Prizes may be picked up then. 2:00-2:45 Utah/Idaho FIRST Robotics Grudge Match—Finals 2:30-3:45 Mindstorm Competitions Maple Terrace USU PHYSICS DAY 3:30 Awards Ceremony in Davis Pavilion Davis Pavilion 9:30 All rides close 10:00 Park closes AT Sky Drop Contest 10:00-12:00 Registration for the Sky Drop is open Drop Site 11:00-1:30 Eggs can be dropped from the Sky Coaster. Drop Site Line will close at 1:00, or as soon as the line is finished. 2:30 Winners will be announced as soon as the contest is judged. Drop Site Colossus’ Colossal G-Forces Contest 9:30-10:30 Contest registration & safety approval inspections Davis Pavilion 10:30-12:30 Colossus open for measurements Colossus May 15, 2020 2:00 Entry forms due Davis Pavilion Physics Bowl Competition (Bighorn Pavilion) 9:30 - 10:30 Contest registration Bighorn Pavilion 10:20 Rules Review/Contest Information/Round 1 time slots Drawing Bighorn Pavilion 10:30 – 11:00 Preliminary
    [Show full text]
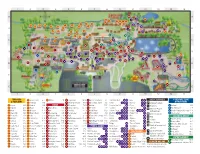
  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 a B C D E F G a B C D E F G 1 2 3 4
    1 2 3 4 5 6 7 8 9 10 11 12 13 14 A 44 A 23 37 G 28 35 36 32 31 30 29 14 16 34 33 12 22 24 1 3 4 10 11 2 5 6 13 15 43 21 9 B G B 20 7 8 17 18 3 19 4 24 27 5 6 19 25 20 21 7 C 25 C 22 23 6 12 3 4 2 45 1 2 18 28 3 6 13 16 19 30 1 G 7 17 23 2 15 31 D 2 20 25 27 D 10 29 32 3 G G G 21 G 26 5 1 8 4 12 1 33 G 34 G 1 5 G 24 G 14 1 6 G 9 22 G 13 G G 18 11 11 42 G 5 G G 8 E 4 10 35 E 9 15 G 7 40 41 16 36 14 2 G 4 F 37 F 3 39 17 38 G G 1 2 3 4 5 6 7 8 9 10 11 12 13 14 TERRACES 21 Group Foods 4-C 16 Willow 7-B 43 Log Flume 10-B 11 Space Scrambler 3-E Cinnamon Roll 9 21 Milk 2 9 GUEST SERVICES X-VENTURE ZONE & PAVILIONS ATTRACTIONS 34 Irontown 9-B 24 Merry-Go-Round 9-D 23 Speedway Junior 9-D Coffee 2 9 19 Nachos 10 25 Drinking Fountain 13 Aspen 6-B 12 Juniper 6-B RIDES 18 Moonraker 7-D 39 Spider 11-F Corn on the Cob 22 Pizza 4 10 Telephone 1 Catapult 2-D 9 Bighorn 4-B Maple 6-C 25 Baby Boats 9-D 36 Musik Express 14-E 22 Terroride 7-E Corndog 10 15 Popcorn 7 Strollers, Wagons 2 Top Eliminator 2-F 15 Birch 6-B 22 Meadow 3-C 12 Bat 4-C 13 OdySea 5-C 31 Tidal Wave 10-D Cotton Candy 7 9 13 Pretzel 4 10 13 21 & Wheelchairs 3 Double Thunder Raceway 3-F 7 Black Hills 3-B 31 Miners Basin 9-A 9 Boomerang 3-E 5 Paratrooper 2-E 10 Tilt-A-Whirl 3-E Dip N Dots5 7 12 18 24 Pulled Pork 22 Gifts & Souvenirs 4 Sky Coaster 4-E 17 Bonneville 5-B 24 Oak 5-C 15 Bulgy the Whale 7-D 28 Puff 9-C 32 Turn of the Century 11-D Floats 9 16 23 Ribs 22 ATM LAGOON A BEACH 10 Bridger 4-B 36 Park Valley 8-A 40 Cliffhanger 11-E 44 Rattlesnake Rapids 10-A 38 Wicked 12-G Frozen 1 11 17
    [Show full text]
  • Cedar Point Welcomes 2016 Golden Ticket Awards Ohio Park and Resort Host Event for Second Time SANDUSKY, Ohio — the First Chapter in Cedar and Beyond
    2016 GOLDEN TICKET AWARDS V.I.P. BEST OF THE BEST! TM & ©2016 Amusement Today, Inc. September 2016 | Vol. 20 • Issue 6.2 www.goldenticketawards.com Cedar Point welcomes 2016 Golden Ticket Awards Ohio park and resort host event for second time SANDUSKY, Ohio — The first chapter in Cedar and beyond. Point's long history was written in 1870, when a bath- America’s top-rated park first hosted the Gold- ing beach opened on the peninsula at a time when en Ticket Awards in 2004, well before the ceremony such recreation was finding popularity with lake island continued to grow into the “Networking Event of the areas. Known for an abundance of cedar trees, the Year.” At that time, the awards were given out be- resort took its name from the region's natural beauty. low the final curve of the award-winning Millennium It would have been impossible for owners at the time Force. For 2016, the event offered a full weekend of to ever envision the world’s largest ride park. Today activities, including behind-the-scenes tours of the the resort has evolved into a funseeker’s dream with park, dinners and receptions, networking opportuni- a total of 71 rides, including one of the most impres- ties, ride time and a Jet Express excursion around sive lineups of roller coasters on the planet. the resort peninsula benefiting the National Roller Tourism became a booming business with the Coaster Museum and Archives. help of steamships and railroad lines. The original Amusement Today asked Vice President and bathhouse, beer garden and dance floor soon were General Manager Jason McClure what he was per- joined by hotels, picnic areas, baseball diamonds and sonally looking forward to most about hosting the a Grand Pavilion that hosted musical concerts and in- event.
    [Show full text]
  • Michael James Elliott Last Updated:2007-08-09
    Rollercoaster List Name: Michael James Elliott Last Updated:2007-08-09 Year Year Roller Coaster Name Park Name Type Current Status Opened Built 1 Alpengeist Busch Gardens Williamsburg Steel-Inverted 1997 1997 Operating 2 Big Bad Wolf Busch Gardens Williamsburg Steel-Suspended 1984 1984 Operating 3 Drachen Fire Busch Gardens Williamsburg Steel-Sit Down 1992 1992 Scrapped 4 Loch Ness Monster Busch Gardens Williamsburg Steel-Sit Down 1978 1978 Operating 5 Big Dipper Camden Park Wood-Classic 1958 1958 Operating 6 Haunted House Camden Park Haunted House-WildMouse Operating 7 Lil' Dipper Camden Park Wood-Classic 1961 1961 Operating 8 Canobie Corkscrew Canobie Lake Park Steel-Looping 1987 1975 Operating 9 Dragon Canobie Lake Park Steel-Kiddie 1991 Operating 10 Borg Assilimator Carowinds Steel-Flying 2004 2000 Relocated from CA 11 Carolina Cyclone Carowinds Steel-Looping 1980 1980 Operating 12 Caroline Goldrusher Carowinds Mine Train 1973 1973 Operating 13 Fairly Odd Coaster (Scooby Doo) Carowinds Wood 1975 1975 No Longer Classic 14 Hurler Carowinds Wood 1994 1994 Operating 15 Rugrats Runaway Reptar Carowinds Steel-Inverted 2003 2003 Operating 16 Thunder Road Carowinds Wood-Racing 1976 1976 Operating 17 Top Gun Carowinds Steel-Inverted 1999 1999 Operating 18 Vortex Carowinds Steel-Stand Up 1992 1992 Operating 19 Yankee Cannonball Canobie Lake Park Wood 1936 1930 Operating 20 Blue Streak Cedar Point Wood-Classic 1964 1964 No Longer Classic 21 Cedar Creek Mine Ride Cedar Point Steel-Sit Down 1969 1969 Operating 22 Corkscrew Cedar Point Steel-Looping 1976 1976 Operating 23 Disaster Transport Cedar Point Bobsled 1990 1985 Operating 24 Gemini Cedar Point Steel-Racing 1978 1978 Operating 25 Iron Dragon Cedar Point Steel-Suspended 1987 1987 Operating 26 Jr.
    [Show full text]
  • New Provost Introduces Himself to Faculty
    .. --------------------------------------------------------------------------------------~----------- THE The Independent Newspaper Serving Notre Dame and Saint Mary's VOLUME 40: ISSUE 16 TUESDAY, SEPTEMBER 13,2005 NDSMCOBSERVER.COM New provost introduces himself to faculty provostship over presidency. Burish - Burish emphasizes ND's also a former Vanderbilt provost and Notre Dame graduate - gave morP Sl'ri­ quest to be even greater ous reasons for coming back to South Bend. By MADDIE HANNA "In addition to my family. two of thl' Associ are News Ediror most important things in my lifn an· my prol'!~ssion.... and my Catholi1: faith." Thomas Burish didn't have a hard timP said Burish. who f'XplainPd how th!'Sf' explaining why he lel't his job as presi­ personal prioritiPs Pach l'artorPd into his dent of Washington and LPe Univ1~rsity dncision. to brcornP tlw next provost of NotrP "What's most important to mf' profPs­ Dame in his address to faculty membPrs sionally is to lw at a gn•at arad!'mir Monday. institution that aspirns to lw gr!'atnr," ll!l rocalled a conversation with a Burish said. "Notre Danw now is a gn•at female freshman student about her institution of higher education ... but dorm shelves. cluttered with pictures of this University seeks to progress PV!'n male celebrities. farther. as all great universities do. It is "Then she said to me, unnecessarily I perhaps a feature of greatness, to aspire• thought, 'President Burish, I'd be happy to be even more." . to put your photograph up there too,"' Given the University's "wonderful. TIM SULLIVAN/The Observer Burish said, provoking hearty laughter.
    [Show full text]
  • Seaworld® Gives Back
    SeaWorld ® Gives Back FROM PARK TO PLANET A Commitment to Education Guests who pass through the gates of one of our parks will benefit from educational experiences intended to inspire a deeper understanding, respect and desire to protect all wildlife. The parks’ educational programs have helped schools, teachers, children and adults explore our world and its inhabitants. We offer our guests countless informal teaching experiences inside the parks including educators, show and exhibit narrations, and interpretive and interactive graphics. Wildlife Rescue With a legacy of animal rescue spanning more than 50 years and benefiting more than 36,000 animals and counting, responding to wildlife in crisis is a commitment we take to heart. Working in partnership with federal, state and local agencies, our rescue teams are on call 24/7 assisting animals that are orphaned, ill, injured or in need of expert care. Our goal is to successfully rehabilitate animals for return to the wild. The small percentage of animals whose injuries are too debilitating to permit release are given lifelong care. Conservation The SeaWorld® & Busch Gardens® Conservation Fund is just one way our guests can get involved in conservation. The fund supports wildlife research, habitat protection, animal rescue, and conservation education in the U.S. and countries all over the world. The fund provides a direct outlet for park visitors to support wildlife, SeaWorld Parks & Entertainment provides all administrative and development costs, staffing, and infrastructure, committing 100 percent of donations to on-the-ground wildlife conservation efforts. SeaWorldCares.com We are proudly accredited by SeaWorld Orlando has been designated a Certified Autism Center © Manta , FLORIDA Clyde & Seamore’s Sea Lion High ORLANDO Sesame Street Land™ USA Today’s 10Best New Attraction Animal Experiences Rides Antarctica: Empire of the Penguin® NEW! Ice Breaker™ Explore the majestic grandeur of the South Pole and see it through the penguins eyes on a first-of-its-kind family ride.
    [Show full text]
  • Rides Theatres & Attractions Games & Arcades Food Stands
    Rides Food Stands & Midway Carrousel Restaurants Demon Drop Hurricane Hannah’s Featuring Sandwiches & Pizza Sky Ride with a Caribbean Flair; Draught Beer Raptor Donut Time Freshly-Made Donuts, Giant Cinnamon Rolls, Sandcastle Blue Streak Muffins, Cookies, Specialty Breads, Juices, Milk, Fresh- Suites Hotel Calypso Brewed Starbucks Coffee Camper Village/ Turnpike Cars Toft’s Ice Cream Parlor Featuring Toft’s Ice Cream, Lighthouse Point Soda Fountain Treats, Sundaes & More. Cedar Downs Cadillac Cars Midway Market All-You-Can-Eat, One-Price, American & International Dinner & Luncheon Menus, Children’s Dodgem Favorites WildCat Johnny Rockets Full-Service Favorite ’40s Menu: CP & LE Railroad Specialty Burgers, Salads, Creamy Shakes & Malts Iron Dragon Kiddieland Refreshments Freshly-Made Sandwiches Mantis & Salads, Hot Dogs, ICEE Frozen Beverages, Special Millennium Force Desserts & Kiddy Meals Thunder Canyon Hot Potato Homemade French Fries, Garlic Fries Wave Swinger Game Day Grille Nachos, Onion Rings, Buffalo Wings, Antique Cars Steak Burgers, Chili, Salads, Lobster & Shrimp Bisque; Snake River Falls Draught Beer soak city Burger Patio Charbroiled Burgers & Fries waterpark Skyhawk Cedar Creek Mine Ride Subway Fresh Sub Sandwiches Made to Order Maverick Coasters Drive-In Restaurant presented by Pepsi® Mean Streak Specialty Sirloin Beef Burgers, Creamy Shakes & Malts, Favorite ’50s Menu Gemini Panda Express® Egg Rolls, Chow Mein, Camp Snoopy Snoopy Bounce, Tilt-a-Whirl, Kung Pao Chicken, Rice & More PEANUTS™ 500, Woodstock Express, Red Baron,
    [Show full text]
  • Adventuring with Books: a Booklist for Pre-K-Grade 6. the NCTE Booklist
    DOCUMENT RESUME ED 311 453 CS 212 097 AUTHOR Jett-Simpson, Mary, Ed. TITLE Adventuring with Books: A Booklist for Pre-K-Grade 6. Ninth Edition. The NCTE Booklist Series. INSTITUTION National Council of Teachers of English, Urbana, Ill. REPORT NO ISBN-0-8141-0078-3 PUB DATE 89 NOTE 570p.; Prepared by the Committee on the Elementary School Booklist of the National Council of Teachers of English. For earlier edition, see ED 264 588. AVAILABLE FROMNational Council of Teachers of English, 1111 Kenyon Rd., Urbana, IL 61801 (Stock No. 00783-3020; $12.95 member, $16.50 nonmember). PUB TYPE Books (010) -- Reference Materials - Bibliographies (131) EDRS PRICE MF02/PC23 Plus Postage. DESCRIPTORS Annotated Bibliographies; Art; Athletics; Biographies; *Books; *Childress Literature; Elementary Education; Fantasy; Fiction; Nonfiction; Poetry; Preschool Education; *Reading Materials; Recreational Reading; Sciences; Social Studies IDENTIFIERS Historical Fiction; *Trade Books ABSTRACT Intended to provide teachers with a list of recently published books recommended for children, this annotated booklist cites titles of children's trade books selected for their literary and artistic quality. The annotations in the booklist include a critical statement about each book as well as a brief description of the content, and--where appropriate--information about quality and composition of illustrations. Some 1,800 titles are included in this publication; they were selected from approximately 8,000 children's books published in the United States between 1985 and 1989 and are divided into the following categories: (1) books for babies and toddlers, (2) basic concept books, (3) wordless picture books, (4) language and reading, (5) poetry. (6) classics, (7) traditional literature, (8) fantasy,(9) science fiction, (10) contemporary realistic fiction, (11) historical fiction, (12) biography, (13) social studies, (14) science and mathematics, (15) fine arts, (16) crafts and hobbies, (17) sports and games, and (18) holidays.
    [Show full text]
  • List of Intamin Rides
    List of Intamin rides This is a list of Intamin amusement rides. Some were supplied by, but not manufactured by, Intamin.[note 1] Contents List of roller coasters List of other attractions Drop towers Ferris wheels Flume rides Freefall rides Observation towers River rapids rides Shoot the chute rides Other rides See also Notes References External links List of roller coasters As of 2019, Intamin has built 163roller coasters around the world.[1] Name Model Park Country Opened Status Ref Family Granite Park United [2] Unknown Unknown Removed Formerly Lightning Bolt Coaster MGM Grand Adventures States 1993 to 2000 [3] Wilderness Run Children's United Cedar Point 1979 Operating [4] Formerly Jr. Gemini Coaster States Wooden United American Eagle Six Flags Great America 1981 Operating [5] Coaster States Montaña Rusa Children's Parque de la Ciudad 1982 Closed [6] Infantil Coaster Argentina Sitting Vertigorama Parque de la Ciudad 1983 Closed [7] Coaster Argentina Super Montaña Children's Parque de la Ciudad 1983 Removed [8] Rusa Infantil Coaster Argentina Bob Swiss Bob Efteling 1985 Operating [9] Netherlands Disaster Transport United Formerly Avalanche Swiss Bob Cedar Point 1985 Removed [10] States Run La Vibora 1986 Formerly Avalanche Six Flags Over Texas United [11] Swiss Bob 1984 to Operating Formerly Sarajevo Six Flags Magic Mountain States [12] 1985 Bobsleds Woodstock Express Formerly Runaway Reptar 1987 Children's California's Great America United [13] Formerly Green Smile 1984 to Operating Coaster Splashtown Water Park States [14] Mine
    [Show full text]
  • BUSCH GARDENS GRAD NITE 2021 Student Guide
    BUSCH GARDENS GRAD NITE May 7, 2021 Student Guide EVENT OVERVIEW It’s been a wild ride for the class of 2021, but now High School Graduates can take their celebration to new heights at Florida’s Thrill Ride Leader with Busch Gardens Grad Nite event! Take on top-rated coasters during an exclusive, after-hours private event for seniors in an electrifying outdoor environment, including DJ music, live entertainment and much more! From the exhilarating launches of Tigris and Cheetah Hunt to the dramatic drops of Falcon’s Fury and SheiKra, this physically distant party packs endless thrills for graduates. This spacious, open-air event offers a one-of-a-kind opportunity for students to celebrate safely with enhanced health and safety measures throughout the park. Grad Nite Exclusive Event Hours: 7:00 p.m. – 12:00 a.m. Students will meet at their school at 5:00 pm and will return to their school at 1:15 am. The cost is $90.00, which includes, entrance to the park, a meal voucher and transportation. Tickets will be on sale through April 23, 2021. No refunds. SAFETY Busch Gardens Tampa Bay is committed to the health and safety of our guests, employees, and the animals in our care. The park has worked diligently with state and local health experts, outside consultants and attraction industry leaders to enhance our already strict health, safety, and cleanliness standards. These protocols and guidelines will be modified based on evolving industry standards and methodologies, public health and governmental directives, and advancing scientific knowledge on the transmissibility of COVID-19.
    [Show full text]
  • Guide for Guests with Disabilities
    Accessibility Guide Busch Gardens® Tampa Bay 1 WELCOME TO BUSCH GARDENS® IN TAMPA BAY, FLORIDA. We’re glad you’re here! This guide provides an overview of services and facilities available for guests with disabilities who are visiting Busch Gardens® in Tampa, Florida. We are committed to providing a safe and enjoyable environment to all guests. Please refer to Guest Relations at the Adventure Outpost if you have any questions. At Busch Gardens®, we have two programs in place to assist guests with disabilities. Our Ride Accessibility Program (RAP) matches the individual abilities of our guests to the requirements of each ride. When enrolled in the RAP, disabled guests will be able to participate in our Special Access Program which assists guests in enjoying attractions throughout the park as some queue lines are not accessible to mobility-impaired guests. These programs are described below. Ride Accessibility Program (RAP): Is designed to allow guests to fully participate and enjoy our parks while keeping in mind the safety requirements of our rides and attractions. The Program was developed based on the requirements of the manufacturer and by evaluating the physical and mental attributes required to safely ride each ride and participate in our other attractions. It is our policy to allow anyone to ride our rides and enjoy our attractions so long as they meet all of these requirements and such that it does not present a potential hazard to the guest or others. Special Access: Is designed to allow our guests to enjoy our attractions without waiting in queue lines due if the guest is not able to do so as a result of his/her disability.
    [Show full text]