Development of an Algebraic Model of Empirical Parameterization of Near Wakes Around a Vehicle
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

2017 Mustang Fastback & Convertible
STANDARD FEATURES 12-volt powerpoints (2) Mirrors – Power sideview with integrated Air conditioning blind spot mirrors 2017 MUSTANG FASTBACK & CONVERTIBLE Ambient lighting (Premium only) Power windows and door locks Rear sequential light-emitting diode (LED) 1 Audio – Premium AM/FM stereo/single-CD Sports Car Class player and clock turn signal lamps ® Models: V6, EcoBoost, EcoBoost Premium, GT, GT Premium Audio – SiriusXM® Satellite Radio with Rear-wheel drive (RWD) 6-month trial subscription (Premium only) Remote Keyless Entry System Cruise control Selectable-effort electronic Engine – 3.7L Ti-VCT V6 (V6 only) power-assisted steering ® Engine – 2.3L EcoBoost® I-4 (EcoBoost only) SYNC with 4.2" color LCD screen in center stack Engine – 5.0L Ti-VCT V8 (GT only) SYNC 3 with 8" LCD capacitive touchscreen with AppLink,™ 911 Assist® and 2 smart-charging Front and rear stabilizer bars USB ports (Premium only) Intelligent Access with push-button start Tilt/telescoping steering column Limited-slip rear differential Transmission – 6-speed manual STANDARD SAFETY & SECURITY AdvanceTrac® electronic stability control LATCH – Lower Anchors and Tether Anchors for Airbags – Driver’s knee, glove-box-door- Children in rear outboard seating positions integrated knee and front-seat side MyKey® Airbags – Side-curtain (fastback only) Perimeter alarm Brakes – 4-wheel Anti-Lock Brake System (ABS) Personal Safety System™ for driver and front Brakes – Power-assisted 4-wheel disc passenger with dual-stage front airbags Illuminated Entry System Rear view camera ® Individual Tire Pressure Monitoring System SecuriLock Passive Anti-Theft System (TPMS; excludes spare) Side-intrusion door beams SOS Post-Crash Alert System™ AVAILABLE FEATURES Adaptive cruise control and forward collision Reverse Sensing System warning with brake support, and rain-sensing Transmission – 6-speed SelectShift® automatic windshield wipers with paddle shifters, and Remote Start System Audio – Shaker™ Pro Audio System Mustang GT Premium. -

Automobile Engineering ) Model Answer
MAHARASHTRA STATE BOARD OF TECHNICAL EDUCATION (Autonomous) (ISO/IEC - 27001 - 2005 Certified) _____________________________________________________________________________________________ WINTER – 15 EXAMINATION Subject Code: 17526 (Automobile Engineering ) Model Answer Important Instructions to examiners: 1) The answers should be examined by key words and not as word-to-word as given in the model answer scheme. 2) The model answer and the answer written by candidate may vary but the examiner may try to assess the understanding level of the candidate. 3) The language errors such as grammatical, spelling errors should not be given more Importance (Not applicable for subject English and Communication Skills). 4) While assessing figures, examiner may give credit for principal components indicated in the figure. The figures drawn by candidate and model answer may vary. The examiner may give credit for any equivalent figure drawn. 5) Credits may be given step wise for numerical problems. In some cases, the assumed constant values may vary and there may be some difference in the candidate’s answers and model answer. 6) In case of some questions credit may be given by judgement on part of examiner of relevant answer based on candidate’s understanding. 7) For programming language papers, credit may be given to any other program based on equivalent concept. --------------------------------------------------------------------------------------------------------------------- Q1.A ( a) Functions of transmission system of an automobile like, (1M per point) i. To transmit power from the engine to the rear wheels of the VEHICLE, ii. To make reduced speed available, to rear wheels of the VEHICLE, iii. To alter the ratio of wheel speed and engine speed/torque in order to suit the field conditions and iv. -

Revology 1968 Mustang Gt 2+2 Fastback Models, Colors, Trim and Wheel Options Colors
REVOLOGY 1968 MUSTANG GT 2+2 FASTBACK MODELS, COLORS, TRIM AND WHEEL OPTIONS COLORS VINTAGE SOLID VINTAGE METALLIC CONTEMPORARY CANDY APPLE RED ACAPULCO BLUE METALLIC ARGENTO NURBURGRING RAVEN BLACK BRITTANY BLUE METALLIC CARRERA WHITE METALLIC WIMBLEDON WHITE SUNLIT GOLD METALLIC CHALK MEADOWLARK YELLOW LIME GOLD METALLIC GIALLO MODENA DIAMOND BLUE METALLIC JET BLACK METALLIC PRESIDENTIAL BLUE METALLIC LAVA ORANGE HIGHLAND GREEN METALLIC MIAMI BLUE GULFSTREAM AQUA NEBULA GRAY PEARL TAHOE TURQUOISE METALLIC ROSSO CORSA ROYAL MAROON METALLIC 1| COLORS GT STRIPES BLACK BLUE RED WHITE REVOLOGY 1965-1966 MUSTANG GT CONVERTIBLE 2| GT STRIPES WHEELS AMERICAN RACING MAGNUM AMERICAN RACING CLASSIC 500 VN500, 17x8 AND 17x9.5 TORQ THRUST VN215, 17x8 AND 17x9.5 REVOLOGY 1965-1966 MUSTANG GT CONVERTIBLE AMERICAN RACING SHELBY FORGELINE DS3, 17x10 FORGELINE GZ3, 17x10 VN427, 17x8 AND 17X9.5 3| WHEELS SPECIAL EDITION FEATURE PACKAGE BLACK INTERIOR WITH QUARTER 17” CLASSIC TORQ THRUST WHEELS WITH DELETE QUARTER PANEL ORNAMENTS CUT WALNUT TRIM DARK CHARCOAL GRAY PAINTED CENTERS AND ROCKER PANEL MOLDINGS REVOLOGY 1965-1966 MUSTANG GT CONVERTIBLE SATIN BLACK PAINTED LAMP PANEL DELETE SIDE EMBLEMS, SIDE STRIPES DUAL EXHAUST WITH CHROME AND TAIL LAMP BEZELS AND HORSE & CORRAL TIPS 4|SPECIAL EDITION FEATURE PACKAGE INTERIOR COLORS STANDARD LEATHERETTE TRIM FULL NAPPA LEATHER TRIM BLACK BLACK, PORSCHE RED, PORSCHE IVORY, MERCEDES CHARCOAL GRAY, SCHWARZ FLAMENCOROT PORZELLAN PORSCHE ACHATGRAU RED LIGHT BEIGE, NAVY BLUE, PORSCHE BROWN, MERCEDES MEDIUM TAN, FERRARI -
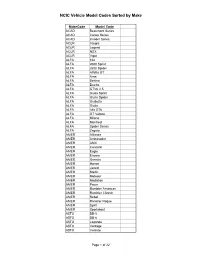
NCIC Vehicle Model Codes Sorted by Make
NCIC Vehicle Model Codes Sorted by Make MakeCode Model Code ACAD Beaumont Series ACAD Canso Series ACAD Invader Series ACUR Integra ACUR Legend ACUR NSX ACUR Vigor ALFA 164 ALFA 2600 Sprint ALFA 2600 Spider ALFA Alfetta GT ALFA Arna ALFA Berlina ALFA Duetto ALFA GTV6 2.5 ALFA Giulia Sprint ALFA Giulia Spider ALFA Giulietta ALFA Giulia ALFA Alfa GT6 ALFA GT Veloce ALFA Milano ALFA Montreal ALFA Spider Series ALFA Zagato AMER Alliance AMER Ambasador AMER AMX AMER Concord AMER Eagle AMER Encore AMER Gremlin AMER Hornet AMER Javelin AMER Marlin AMER Matador AMER Medallion AMER Pacer AMER Rambler American AMER Rambler Classic AMER Rebel AMER Rambler Rogue AMER Spirit AMER Sportabout ASTO DB-5 ASTO DB-6 ASTO Lagonda ASTO Vantage ASTO Volante Page 1 of 22 NCIC Vehicle Model Codes Sorted by Make MakeCode Model Code ASUN GT ASUN SE ASUN Sunfire ASUN Sunrunner AUDI 100 AUDI 100GL AUDI 100LS AUDI 200LS AUDI 4000 AUDI 5000 AUDI 850 AUDI 80 AUDI 90 AUDI S4 AUDI Avant AUDI Cabriolet AUDI 80 LS AUDI Quattro AUDI Super 90 AUDI V-8 AUHE 100 Series AUHE 3000 Series AUHE Sprite AUST 1100 AUST 1800 AUST 850 AUST A99 & 110 AUST A40 AUST A55 AUST Cambridge AUST Cooper "S" AUST Marina AUST Mini Cooper AUST Mini AUST Westminster AVTI Series A AVTI Series B BENT Brooklands BENT Continental Convertible BENT Corniche BENT Eight BENT Mulsanne BENT Turbo R BERO Cabrio BERO Palinuro BERO X19 BMC Princess BMW 2002 Series BMW 1600 Page 2 of 22 NCIC Vehicle Model Codes Sorted by Make MakeCode Model Code BMW 1800 BMW 200 BMW 2000 Series BMW 2500 Series BMW 2.8 BMW 2800 -

Vehicle Make, Vehicle Model
V8, V9 VEHICLE MAKE, VEHICLE MODEL Format: VEHICLE MAKE – 2 numeric VEHICLE MODEL – 3 numeric Element Values: MAKE: Blanks 01-03, 06-10, 12-14, 18-25, 29-65, 69-77, 80-89, 90-94, 98-99 MODEL: Blanks 001-999 Remarks: SEE REMARKS UNDER VEHICLE IDENTIFICATION NUMBER – V12 2009 181 ALPHABETICAL LISTING OF MAKES FARS MAKE MAKE/ NCIC FARS MAKE MAKE/ NCIC MAKE MODEL CODE* MAKE MODEL CODE* CODE TABLE CODE TABLE PAGE # PAGE # 54 Acura 187 (ACUR) 71 Ducati 253 (DUCA) 31 Alfa Romeo 187 (ALFA) 10 Eagle 205 (EGIL) 03 AM General 188 (AMGN) 91 Eagle Coach 267 01 American Motors 189 (AMER) 29-398 Excaliber 250 (EXCL) 69-031 Aston Martin 250 (ASTO) 69-035 Ferrari 251 (FERR) 32 Audi 190 (AUDI) 36 Fiat 205 (FIAT) 33 Austin/Austin 191 (AUST) 12 Ford 206 (FORD) Healey 82 Freightliner 259 (FRHT) 29-001 Avanti 250 (AVTI) 83 FWD 260 (FWD) 98-802 Auto-Union-DKW 269 (AUTU) 69-398 Gazelle 252 (GZL) 69-042 Bentley 251 (BENT) 92 Gillig 268 69-052 Bertone 251 (BERO) 23 GMC 210 (GMC) 90 Bluebird 267 (BLUI) 25 Grumman 212 (GRUM) 34 BMW 191 (BMW) 72 Harley- 253 (HD) 69-032 Bricklin 250 (BRIC) Davidson 80 Brockway 257 (BROC) 69-036 Hillman 251 (HILL) 70 BSA 253 (BSA) 98-806 Hino 270 (HINO) 18 Buick 193 (BUIC) 37 Honda 213 (HOND) 19 Cadillac 194 (CADI) 29-398 Hudson 250 (HUDS) 98-903 Carpenter 270 55 Hyundai 215 (HYUN) 29-002 Checker 250 (CHEC) 08 Imperial 216 (CHRY) 20 Chevrolet 195 (CHEV) 58 Infiniti 216 (INFI) 06 Chrysler 199 (CHRY) 84 International 261 (INTL) 69-033 Citroen 250 (CITR) Harvester 98-904 Collins Bus 270 38 Isuzu 217 (ISU ) 64 Daewoo 201 (DAEW) 88 Iveco/Magirus -

Fuel Efficient Road Transport System : a Review
International Journal of Engineering Research & Technology (IJERT) ISSN: 2278-0181 Vol. 3 Issue 11, November-2014 Fuel Efficient Road Transport System : A Review Telem Bishworjit Singh Dr. Th. Kiranbala Devi M.Tech. Student,Civil Engg. Dept. Faculty, Department of Civil Engineering NIT Silchar, Assam, India Manipur Institute of Technology Manipur, India Abstract - For developing a better economy there is a need of developing an energy-efficient and environment friendly road transport system. India is one of the fastest growing and largest emerging market economies. The Indian economy is one of the fastest growing economies and is the 12th largest in terms of the market exchange rate at $1,430.02 billion (2010 India GDP). In terms of purchasing power parity, the Indian economy ranks the fourth largest in the world. By 2020, India is expected to be in the top 10 largest economies of the world. Rapid economic growth is usually connected to a rapid expansion and highly profitable road transportation. Transportation is a major consumer of petroleum fuels whose prices are set to rise due to the decreasing reserves. There is a need of a more efficient transportation system. Key Words: Transportation, petroleum fuels, consumer, transport system, economies INTRODUCTION India is one of the fastest growing and largest emerging market economies (Wilson and Purushothaman, 2003;IJERTIJERT Economy Watch, 2010). According to W.H.O. the population of India is almost 1,245,910,000 (June 27, 2014) i.e. 17.4% billion people of the total population of the world. To support the population, huge amount of petroleum energy is being consumed in highway transportation sector which in turn cost a huge amount of Indian rupees. -

A Comparison of Electric Vehicles and Conventional Automobiles: Costs and Quality Perspective
A Comparison of Electric Vehicles and Conventional Automobiles: Costs and Quality Perspective Marek Palinski Bachelor thesis in Business Administration BACHELOR’S THESIS Author: Marek Palinski Degree Program: Business Administration Specialization: Marketing Supervisor: Thomas Finne Title: A Comparison of Electric Vehicles and Conventional Automobiles: Costs and Quality Perspective _________________________________________________________________________ Date: 7th April 2017 Number of pages: 60 Appendices: 1 _________________________________________________________________________ Abstract: This report covers the research area of electric vehicles dedicated for personal transportation and its relevant market including the necessary to know background information about the topic. Since the newly developed car market area of e-mobility has not experienced a long presence on the global personal vehicle market, the report is focusing on the research of current situation for the buyers and the less and more favorable conditions in different countries. The core of the report is a comparative research of BEV, PHEV and conventional types of vehicles with their real market costs situation of spring 2017. The three mentioned propulsion systems vehicles are put into test and finally delivering the true cost to own of each particular one, while considering their propulsion system related quality features as well. Ongoing, the researched assumptions are later on put into test in the form of a questionnaire focusing on finding out about the awareness of electric vehicles among the publicity nowadays. The final statement that is going to be approved or rejected is the electric vehicles as the future of the global car market. _________________________________________________________________________ Language: English Key words: electric vehicles, battery electric vehicles, plug-in hybrid vehicles, conventional vehicles, global car market _________________________________________________________________________ Table of Contents 1. -

Missing Child Report Florida Safe Families Network Reference Data
Missing Child Report Florida Safe Families Network Reference Data FSFN Missing Child Report Page: Tab Child Information Name: Field District Name: District 1 District 2 District 3 District 4 District 7 District 8 District 9 District 10 District 11 District 12 District 13 District 14 District 15 Suncoast District FSFN Missing Child Report Page: Tab Child Information Name: Field Eye Color Name: Black Blue Brown Dark Gray Green Hazel Light FSFN May 12, 2017 Page 1 Missing Child Report Florida Safe Families Network Reference Data Pink Unknown FSFN Missing Child Report Page: Tab Child Information Name: Field Hair Color Name: Auburn Bald Black Blonde Brown Grey Lt. Brown Other Red Salt & Pepper Sandy Unknown White FSFN Missing Child Report Page: Tab Child Information Name: Field Build Name: Heavy Medium Muscular Thin Unknown FSFN May 12, 2017 Page 2 Missing Child Report Florida Safe Families Network Reference Data FSFN Missing Child Report Page: Tab Child Information Name: Field Complexion Name: Albino Black Dark Dark Brown Fair Freckles Light Light Brown Medium Medium Brown Olive Ruddy Sallow Yellow FSFN Missing Child Report Page: Tab Child Information Name: Field Teeth Name: Braces Broken/Chipped Crooked Decayed Dirty/Stained FALSE Gapped Gold FSFN May 12, 2017 Page 3 Missing Child Report Florida Safe Families Network Reference Data Irregular Missing Normal Protruding Retainer Silver Unknown Very White FSFN Missing Child Report Page: Tab Child Information Name: Field Scar/Marks Name: Acne Amputee Body Piercing Deformity Disability Disfigured -

2021 PRICE CATALOG Auto Custom Carpets, Inc
2021 PRICE CATALOG Auto Custom Carpets, Inc. ACC was founded by Jack Holland and incorporated TABLE OF CONTENTS in October of 1977. Jack had been in the auto trim business for many years before starting Auto Custom Acura .............................................. 10 Carpets. He started out by purchasing the carpet used American Motors ......................... 10 in the molding operation from OEM suppliers such as Austin Healey ................................12 Collins & Aikman, J.P. Stevens and Masland. In April of BMW.................................................12 1984 he purchased Academy Carpets, Inc. in Dalton, Buick ................................................14 Cadillac ...........................................21 GA and began tufting his own carpet. In January Chevrolet ...................................... 25 of 1986 he purchased the plant that was formerly Chrysler ..........................................67 operated by the Automotive Division of E.T. Barwick Desoto ........................................... 69 Mills. For many years, this plant was a prime carpet Dodge .............................................70 supplier to General Motors and Chrysler Corporation. Eagle .............................................. 86 The first molded carpets used in the automotive Edsel ...............................................87 industry were developed at this plant in 1958. By Fiat ...................................................88 Jack Holland, purchasing this plant, ACC was not dependent upon Ford .................................................88 -

Official Online Magazine of the Mustang Six Association
August 21, 2015 VOLUME NO. 2 ISSUE NO. 14 Official Online Magazine of the Mustang Six Association A BIRTHDAY PRESENT MUSTANG IT’S NOT “JUST A SIX”, IT’S A PART OF THE LEGACY OF THE MUSTANG! WEBSITE FACEBOOK E-MAIL NATIONAL DIRECTOR FACEBOOK FORUM FOUNDER TERRY REINHART WADE SOVONICK ADAM SPARKS RICK MITCHELL DO WE HAVE YOUR SIX YET? CONTENTS Members Mustangs 4 INLINE 6 CLASSICS 6 A TAIL OF TWO PONIES 8 SIX CUSTOMS 9 V-6 CONNECTION 13 MUSTANG SIX SHOWCASE A FULL HOUSE 6 Articles 14 OLD SCHOOL OLD GEEZER 16 FOUNDER’S CORNER Departments HE DID, SO SHE DID 13 3 STABLE STATEMENTS 17 M6A AT THE SHOWS 19 M6A LOGOS 21 M6A’s NATIONAL CAR SHOW 22 SUPPORTERS OF M6A 23 SHOW FLYER M6A ON THE ROAD 19 24 THE PONY STOPS HERE THE M6A LOGO, M6A, THE MUSTANG SIX ASSOCIATION COPYRIGHT 2015 2 STABLE STATEMENTS ll I can say is WOW, the last three weeks have been amazing for M6A. In one day alone we added almost A40 members to our rolls, and we now have almost 750 members! I want to give a great big thanks to two individu- als who have really helped spread the word about M6A and who we are. First is Rob Kinnan, editor of Mustang Monthly, he featured a write up on the Mustang360 website, about M6A and the show. The other is Steve, who sends out “The Mustang Express” a weekly newsletter featuring MCA events and clubs. He published a story about M6A and in another edition listed our show and links. -

US EPA 86.1803-01 Definitions § 86.1803–01 40 CFR Ch
Appendix B US EPA 86.1803-01 Definitions § 86.1803–01 40 CFR Ch. I (7–1–11 Edition) applicable for the appropriate model ble hose connections; the number of year. high side service ports; the number of low side service ports; the number of § 86.1803–01 Definitions. switches, transducers, and expansion The following definitions apply to valves; the number of TXV refrigerant this subpart: control devices; the number and type of 505 Cycle means the test cycle that heat exchangers, mufflers, receiver/ consists of the first 505 seconds (sec- dryers, and accumulators; and the onds 1 to 505) of the EPA Urban Dyna- length and type of flexible hose (e.g., mometer Driving Schedule, described rubber, standard barrier or veneer, in § 86.115–00 and listed in appendix I, ultra-low permeation). paragraph (a), of this part. Alternative fuels means any fuel other 866 Cycle means the test cycle that than gasoline and diesel fuels, such as consists of the last 866 seconds (seconds methanol, ethanol, and gaseous fuels. 506 to 1372) of the EPA Urban Dyna- Approach angle means the smallest mometer Driving Schedule, described angle in a plan side view of an auto- in § 86.115–00 and listed in appendix I, mobile, formed by the level surface on paragraph (a), of this part. which the automobile is standing and a Abnormally treated vehicle means any line tangent to the front tire static diesel light-duty vehicle or diesel light- loaded radius arc and touching the un- duty truck that is operated for less derside of the automobile forward of than five miles in a 30 day period im- the front tire. -

The 1964 Rambler Tarpon Concept Car Article from Fish Tales
Marlin History The 1964 Rambler Tarpon Concept Car By Joe Howard, Fish Tales Editor Vol 9 No 1, March 2008 Distinctive! Different! That best describes the AMC Marlin. There certainly was nothing else like it on the road when it debuted in 1965. How did the Marlin come to be? How did the design concept begin? Viewing the Marlin in retrospect, we can see that it has proven to be one of the most popular of all collectible AMCs. Let’s look back and see how this unique automobile started. Early in 1963, American Motors management started angling for “a new car with a sports flair”. Richard (Dick) Teague, then AM’s Director of Styling, and his staff were happy to comply. Their average age hovered around 35, and they were excited about developing a car more suited to younger tastes. One opinion by Jim Alexander, a former AM designer, was that Teague chose a compact fastback because he had heard about Plymouth’s soon-to-be-released Barracuda “and felt that we could do something like that, too”. On the other hand, Vince Geraci, who managed Senior Car exteriors, couldn’t recall any mention of the Barracuda at that time but suggested that Teague “wanted a fighter for the Mustang. [And] we didn’t have the wherewithal that Ford had to retool. We either had to take it off the American body, or off the Classic body”. The 1964 Rambler Tarpon Concept Car Either way, Teague’s answer was a pillarless, fastback roofline grafted on to AM’s entry-level Rambler American.