DOCSLIB.ORG

Linear Algebra I Skills, Concepts and Applications

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Linear Algebra I Skills, Concepts and Applications Linear Algebra I Skills, Concepts and Applications Gregg Waterman Oregon Institute of Technology c 2016 Gregg Waterman This work is licensed under the Creative Commons Attribution 4.0 International license. The essence of the license is that You are free to: Share - copy and redistribute the material in any medium or format • Adapt - remix, transform, and build upon the material for any purpose, even commercially. • The licensor cannot revoke these freedoms as long as you follow the license terms. Under the following terms: Attribution - You must give appropriate credit, provide a link to the license, and indicate if changes • were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use. No additional restrictions - You may not apply legal terms or technological measures that legally restrict others from doing anything the license permits. Notices: You do not have to comply with the license for elements of the material in the public domain or where your use is permitted by an applicable exception or limitation. No warranties are given. The license may not give you all of the permissions necessary for your intended use. For example, other rights such as publicity, privacy, or moral rights may limit how you use the material. For any reuse or distribution, you must make clear to others the license terms of this work. The best way to do this is with a link to the web page below. To view a full copy of this license, visit https://creativecommons.org/licenses/by/4.0/legalcode. Contents 1 Systems of Linear Equations 1 1.1 Linear Equations and Systems of Linear Equations . ......... 2 1.2 Curve Fitting, Temperature Equilibrium and Electric Circuits........... 7 1.3 SolvingSystemsofLinearEquations . ..... 13 1.4 SolvingWithMatrices .............................. 17 1.5 “WhenThingsGoWrong”............................. 25 1.6 BacktoApplications............................... 31 1.7 Chapter1Exercises ................................ 35 2 Euclidean Space and Vectors 40 2.1 EuclideanSpace .................................. 41 2.2 IntroductiontoVectors . .. .. .. 45 2.3 Addition and Scalar Multiplication of Vectors, Linear Combinations . 48 2.4 LinearCombinationFormofaSystem. .... 54 2.5 SetsofVectors................................... 58 2.6 VectorEquationsofLinesandPlanes . ..... 62 2.7 Interpreting Solutions to Systems of Linear Equations . ............ 68 2.8 The Dot Product of Vectors, Projections . ...... 72 3 Matrices and Vectors 76 3.1 IntroductiontoMatrices. ... 78 3.2 MatrixTimesaVector............................... 82 3.3 Actions of Matrices on Vectors: Transformations in R2 ............. 90 3.4 MultiplyingMatrices .............................. .. 94 3.5 InverseMatrices .................................. 102 3.6 Determinants and Systems of Equations . ...... 108 3.7 Applications: Transformation Matrices, Graph Theory . ............ 115 4 Vector Spaces and Subspaces 121 4.1 SpanofaSetofVectors.............................. 122 4.2 ClosureofaSetUnderanOperation . 128 4.3 Vector Spaces and Subspaces . 131 4.4 ColumnSpaceandNullSpaceofaMatrix . 138 4.5 Least Squares Solutions to Inconsistent Systems . .......... 142 4.6 LinearIndependence ............................... 147 4.7 BasesofSubspaces,Dimension . 155 4.8 Bases for the Column Space and Null Space of a Matrix . ....... 160 4.9 SolutionstoSystemsofEquations. ..... 165 4.10Chapter4Exercises ............................... 168 5 Linear Transformations 170 5.1 TransformationsofVectors . 171 5.2 LinearTransformations. 176 5.3 Linear Transformations and Matrices . ...... 183 5.4 CompositionsofTransformations . ..... 186 5.5 Transformations and Homogeneous Coordinates . ........ 190 5.6 An Introduction to Eigenvalues and Eigenvectors . .......... 197 5.7 Finding Eigenvalues and Eigenvectors . ....... 202 i 5.8 DiagonalizationofMatrices . .... 211 5.9 Solving Systems of Differential Equations . ........ 214 A Index of Symbols 216 B Solutions to Exercises 218 B.1 Chapter1Solutions ................................ 218 B.2 Chapter2Solutions ................................ 219 B.3 Chapter3Solutions ................................ 219 B.4 Chapter4Solutions ................................ 220 B.5 Chapter5Solutions ................................ 223 B.6 Chapter6Solutions ................................ 223 B.7 Chapter7Solutions ................................ 224 B.8 Chapter8Solutions ................................ 226 B.9 Chapter9Solutions ................................ 228 B.10Chapter10Solutions. .. .. 230 C Solutions to Exercises 232 C.1 Chapter1Solutions ................................ 232 C.2 Chapter2Solutions ................................ 234 C.3 Chapter3Solutions ................................ 241 C.4 Chapter4Solutions ................................ 247 C.5 Chapter5Solutions ................................ 250 ii 1 Systems of Linear Equations Learning Outcome: 1. Solve systems of linear equations using Gaussian elimination, use systems of linear equations to solve problems. Performance Criteria: (a) Determine whether an equation in n unknowns is linear. (b) Set up a system of linear equations to find coefficients of a line or poly- nomial through a given set of points, or to model flow in a network or equilibrium temperatures in a solid object. (c) Determine whether an n-tuple is a solution to a linear equation or a system of linear equations. (d) Solve a system of two linear equations by the addition method. (e) Give the coefficient matrix and augmented matrix for a system of equa- tions. (f) Determine whether a matrix is in row-echelon form. Perform, by hand, elementary row operations to reduce a matrix to row-echelon form. (g) Determine whether a matrix is in reduced row-echelon form. Use tech- nology to reduce a matrix to reduced row-echelon form. (h) For a system of equations having a unique solution, determine the so- lution from either the row-echelon form or reduced row-echelon form of the augmented matrix for the system. (i) Use a calculator to solve a system of linear equations having a unique solution. (j) Given the row-echelon or reduced row-echelon form of an augmented matrix for a system of equations, determine the leading variables and free variables of the system. (k) Given the row-echelon or reduced row-echelon form for a system of equa- tions: Determine whether the system has a unique solution, and give the • solution if it does. If the system does not have a unique solution, determine whether it • is inconsistent (no solution) or dependent (infinitely many solutions). If the system is dependent, give the general form of a solution and • give some particular solutions. (l) Use systems of equations to solve network problems. 1 1.1 Linear Equations and Systems of Linear Equations Performance Criteria: 1. (a) Determine whether an equation in n unknowns is linear. (b) Set up a system of linear equations to find coefficients of a line or poly- nomial through a given set of points, or to model flow in a network or equilibrium temperatures in a solid object. (c) Determine whether an n-tuple is a solution to a linear equation or a system of linear equations. Linear Equations and Their Solutions It is natural to begin our study of linear algebra with the process of solving systems of linear equations, and applications of such systems. Definition 1.1.1: A linear equation in n unknowns is an equation that can be put in the form a x + a x + a x + + a x = b, (1) 1 1 2 2 3 3 · · · n n where a1, a2, ..., an and b are known constants and x1, x2, ... , xn are unknown values. A solution to a linear equation is a collection of values for the unknowns that makes the equation true. Example 1.1(a): Which of the equations ⋄ y = 2 x + 4 y = 16t2 + 61t + 7 5.3x + 7.2y + 1.4z = 16.9 − 3 − a x + a x + + a x = b , 41 1 42 2 · · · 4n n 4 where a11, a12, ..., a1n, b1 are all known numbers, are linear equations? 2 Solution: The first equation can be rewritten as 3 x + y = 4, so it is a linear equation. The second equation can be written 16t2 + 61t y = 4, but the t2 prevents this from being a − − − linear equation. The third and fourth equations are in exactly the form (1), so they are linear. A few comments are in order: For the third equation above we see that • 5.3(1) + 7.2(2) + 1.4( 2) = 16.9, − so x = 1, y = 2 and z = 2 is a solution to 5.3x + 7.2y + 1.4z = 16.9. To save writing we − usually write such a solution as (1, 2, 2), a form you are likely familiar with. − 2 The equation y = 2 x + 4 can also be rewritten as 2x + 3y = 12 instead of 2 x + y = 4. An • − 3 3 (x,y) pair that is a solution to any one of the forms is also a solution to the other two (and any pair that is NOT a solution to any one of them will not be a solution to the other two either). We can multiply or divide both sides of a linear equation by a value in order to make it easier to work with, if we wish. Although you may have used x and y, or x, y and z as the unknown quantities in the • past, like in the third equation above, we will often use x1, x2, ..., xn instead. Thus the third equation could be written 5.3x1 + 7.2x2 + 1.4x3 = 15.9, which is equivalent to the fourth equation with a41 = 5.3, a42 = 7.2, a43 = 1.4 and b4 = 15.9. One obvious advantage to using the letter a for all of the numbers is that we don’t have to fret about what letters to use, and there is no danger of running out of letters! You will eventually see that there is also a very good mathematical reason for using just x (or some other single letter), with subscripts denoting different values. It is important that you easily recognize the form (1) from the definition of a linear equation. Soon we will be interested in similar equations, but of the form number vector + number vector + + number vector = vector. · · · · · · We now move on to the concept that forms the beginning of our study of linear algebra: Definition 1.1.2: A system of linear equations is a set of linear equations containing the same unknowns. (Not every equation needs to contain every un- known.) A solution to a system of linear equations is a collection of values for the unknowns that makes every equation of the system true.
Load more

Recommended publications
  • Algebra II Level 1
    Algebra II 5 credits – Level I Grades: 10-11, Level: I Prerequisite: Minimum grade of 70 in Geometry Level I (or a minimum grade of 90 in Geometry Topics) Units of study include: equations and inequalities, linear equations and functions, systems of linear equations and inequalities, matrices and determinants, quadratic functions, polynomials and polynomial functions, powers, roots, and radicals, rational equations and functions, sequence and series, and probability and statistics. PROFICIENCIES INEQUALITIES -Solve inequalities -Solve combined inequalities -Use inequality models to solve problems -Solve absolute values in open sentences -Solve absolute value sentences graphically LINEAR EQUATION FUNCTIONS -Solve open sentences in two variables -Graph linear equations in two variables -Find the slope of the line -Write the equation of a line -Solve systems of linear equations in two variables -Apply systems of equations to solve real word problems -Solve linear inequalities in two variables -Find values of functions and graphs -Find equations of linear functions and apply properties of linear functions -Graph relations and determine when relations are functions PRODUCTS AND FACTORS OF POLYNOMIALS -Simplify, add and subtract polynomials -Use laws of exponents to multiply a polynomial by a monomial -Calculate the product of two or more polynomials -Demonstrate factoring -Solve polynomial equations and inequalities -Apply polynomial equations to solve real world problems RATIONAL EQUATIONS -Simplify quotients using laws of exponents -Simplify
    [Show full text]
  • Operations Per Se, to See If the Proposed Chi Is Indeed Fruitful
    DOCUMENT RESUME ED 204 124 SE 035 176 AUTHOR Weaver, J. F. TTTLE "Addition," "Subtraction" and Mathematical Operations. 7NSTITOTION. Wisconsin Univ., Madison. Research and Development Center for Individualized Schooling. SPONS AGENCY Neional Inst. 1pf Education (ED), Washington. D.C. REPORT NO WIOCIS-PP-79-7 PUB DATE Nov 79 GRANT OS-NIE-G-91-0009 NOTE 98p.: Report from the Mathematics Work Group. Paper prepared for the'Seminar on the Initial Learning of Addition and' Subtraction. Skills (Racine, WI, November 26-29, 1979). Contains occasional light and broken type. Not available in hard copy due to copyright restrictions.. EDPS PRICE MF01 Plum Postage. PC Not Available from EDRS. DEseR.TPT00S *Addition: Behavioral Obiectives: Cognitive Oblectives: Cognitive Processes: *Elementary School Mathematics: Elementary Secondary Education: Learning Theories: Mathematical Concepts: Mathematics Curriculum: *Mathematics Education: *Mathematics Instruction: Number Concepts: *Subtraction: Teaching Methods IDENTIFIERS *Mathematics Education ResearCh: *Number 4 Operations ABSTRACT This-report opens by asking how operations in general, and addition and subtraction in particular, ante characterized for 'elementary school students, and examines the "standard" Instruction of these topics through secondary. schooling. Some common errors and/or "sloppiness" in the typical textbook presentations are noted, and suggestions are made that these probleks could lend to pupil difficulties in understanding mathematics. The ambiguity of interpretation .of number sentences of the VW's "a+b=c". and "a-b=c" leads into a comparison of the familiar use of binary operations with a unary-operator interpretation of such sentences. The second half of this document focuses on points of vier that promote .varying approaches to the development of mathematical skills and abilities within young children.
    [Show full text]
  • The Computational Complexity of Polynomial Factorization
    Open Questions From AIM Workshop: The Computational Complexity of Polynomial Factorization 1 Dense Polynomials in Fq[x] 1.1 Open Questions 1. Is there a deterministic algorithm that is polynomial time in n and log(q)? State of the art algorithm should be seen on May 16th as a talk. 2. How quickly can we factor x2−a without hypotheses (Qi Cheng's question) 1 State of the art algorithm Burgess O(p 2e ) 1.2 Open Question What is the exponent of the probabilistic complexity (for q = 2)? 1.3 Open Question Given a set of polynomials with very low degree (2 or 3), decide if all of them factor into linear factors. Is it faster to do this by factoring their product or each one individually? (Tanja Lange's question) 2 Sparse Polynomials in Fq[x] 2.1 Open Question α β Decide whether a trinomial x + ax + b with 0 < β < α ≤ q − 1, a; b 2 Fq has a root in Fq, in polynomial time (in log(q)). (Erich Kaltofen's Question) 2.2 Open Questions 1. Finding better certificates for irreducibility (a) Are there certificates for irreducibility that one can verify faster than the existing irreducibility tests? (Victor Miller's Question) (b) Can you exhibit families of sparse polynomials for which you can find shorter certificates? 2. Find a polynomial-time algorithm in log(q) , where q = pn, that solves n−1 pi+pj n−1 pi Pi;j=0 ai;j x +Pi=0 bix +c in Fq (or shows no solutions) and works 1 for poly of the inputs, and never lies.
    [Show full text]
  • Section P.2 Solving Equations Important Vocabulary
    Section P.2 Solving Equations 5 Course Number Section P.2 Solving Equations Instructor Objective: In this lesson you learned how to solve linear and nonlinear equations. Date Important Vocabulary Define each term or concept. Equation A statement, usually involving x, that two algebraic expressions are equal. Extraneous solution A solution that does not satisfy the original equation. Quadratic equation An equation in x that can be written in the general form 2 ax + bx + c = 0 where a, b, and c are real numbers with a ¹ 0. I. Equations and Solutions of Equations (Page 12) What you should learn How to identify different To solve an equation in x means to . find all the values of x types of equations for which the solution is true. The values of x for which the equation is true are called its solutions . An identity is . an equation that is true for every real number in the domain of the variable. A conditional equation is . an equation that is true for just some (or even none) of the real numbers in the domain of the variable. II. Linear Equations in One Variable (Pages 12-14) What you should learn A linear equation in one variable x is an equation that can be How to solve linear equations in one variable written in the standard form ax + b = 0 , where a and b and equations that lead to are real numbers with a ¹ 0 . linear equations A linear equation has exactly one solution(s). To solve a conditional equation in x, . isolate x on one side of the equation by a sequence of equivalent, and usually simpler, equations, each having the same solution(s) as the original equation.
    [Show full text]
  • Hyperoperations and Nopt Structures
    Hyperoperations and Nopt Structures Alister Wilson Abstract (Beta version) The concept of formal power towers by analogy to formal power series is introduced. Bracketing patterns for combining hyperoperations are pictured. Nopt structures are introduced by reference to Nept structures. Briefly speaking, Nept structures are a notation that help picturing the seed(m)-Ackermann number sequence by reference to exponential function and multitudinous nestings thereof. A systematic structure is observed and described. Keywords: Large numbers, formal power towers, Nopt structures. 1 Contents i Acknowledgements 3 ii List of Figures and Tables 3 I Introduction 4 II Philosophical Considerations 5 III Bracketing patterns and hyperoperations 8 3.1 Some Examples 8 3.2 Top-down versus bottom-up 9 3.3 Bracketing patterns and binary operations 10 3.4 Bracketing patterns with exponentiation and tetration 12 3.5 Bracketing and 4 consecutive hyperoperations 15 3.6 A quick look at the start of the Grzegorczyk hierarchy 17 3.7 Reconsidering top-down and bottom-up 18 IV Nopt Structures 20 4.1 Introduction to Nept and Nopt structures 20 4.2 Defining Nopts from Nepts 21 4.3 Seed Values: “n” and “theta ) n” 24 4.4 A method for generating Nopt structures 25 4.5 Magnitude inequalities inside Nopt structures 32 V Applying Nopt Structures 33 5.1 The gi-sequence and g-subscript towers 33 5.2 Nopt structures and Conway chained arrows 35 VI Glossary 39 VII Further Reading and Weblinks 42 2 i Acknowledgements I’d like to express my gratitude to Wikipedia for supplying an enormous range of high quality mathematics articles.
    [Show full text]
  • Vocabulary Eighth Grade Math Module Four Linear Equations
    VOCABULARY EIGHTH GRADE MATH MODULE FOUR LINEAR EQUATIONS Coefficient: A number used to multiply a variable. Example: 6z means 6 times z, and "z" is a variable, so 6 is a coefficient. Equation: An equation is a statement about equality between two expressions. If the expression on the left side of the equal sign has the same value as the expression on the right side of the equal sign, then you have a true equation. Like Terms: Terms whose variables and their exponents are the same. Example: 7x and 2x are like terms because the variables are both “x”. But 7x and 7ͬͦ are NOT like terms because the x’s don’t have the same exponent. Linear Expression: An expression that contains a variable raised to the first power Solution: A solution of a linear equation in ͬ is a number, such that when all instances of ͬ are replaced with the number, the left side will equal the right side. Term: In Algebra a term is either a single number or variable, or numbers and variables multiplied together. Terms are separated by + or − signs Unit Rate: A unit rate describes how many units of the first type of quantity correspond to one unit of the second type of quantity. Some common unit rates are miles per hour, cost per item & earnings per week Variable: A symbol for a number we don't know yet. It is usually a letter like x or y. Example: in x + 2 = 6, x is the variable. Average Speed: Average speed is found by taking the total distance traveled in a given time interval, divided by the time interval.
    [Show full text]
  • The Evolution of Equation-Solving: Linear, Quadratic, and Cubic
    California State University, San Bernardino CSUSB ScholarWorks Theses Digitization Project John M. Pfau Library 2006 The evolution of equation-solving: Linear, quadratic, and cubic Annabelle Louise Porter Follow this and additional works at: https://scholarworks.lib.csusb.edu/etd-project Part of the Mathematics Commons Recommended Citation Porter, Annabelle Louise, "The evolution of equation-solving: Linear, quadratic, and cubic" (2006). Theses Digitization Project. 3069. https://scholarworks.lib.csusb.edu/etd-project/3069 This Thesis is brought to you for free and open access by the John M. Pfau Library at CSUSB ScholarWorks. It has been accepted for inclusion in Theses Digitization Project by an authorized administrator of CSUSB ScholarWorks. For more information, please contact [email protected]. THE EVOLUTION OF EQUATION-SOLVING LINEAR, QUADRATIC, AND CUBIC A Project Presented to the Faculty of California State University, San Bernardino In Partial Fulfillment of the Requirements for the Degre Master of Arts in Teaching: Mathematics by Annabelle Louise Porter June 2006 THE EVOLUTION OF EQUATION-SOLVING: LINEAR, QUADRATIC, AND CUBIC A Project Presented to the Faculty of California State University, San Bernardino by Annabelle Louise Porter June 2006 Approved by: Shawnee McMurran, Committee Chair Date Laura Wallace, Committee Member , (Committee Member Peter Williams, Chair Davida Fischman Department of Mathematics MAT Coordinator Department of Mathematics ABSTRACT Algebra and algebraic thinking have been cornerstones of problem solving in many different cultures over time. Since ancient times, algebra has been used and developed in cultures around the world, and has undergone quite a bit of transformation. This paper is intended as a professional developmental tool to help secondary algebra teachers understand the concepts underlying the algorithms we use, how these algorithms developed, and why they work.
    [Show full text]
  • 2.3 Solving Linear Equations a Linear Equation Is an Equation in Which All Variables Are Raised to Only the 1 Power. in This
    2.3 Solving Linear Equations A linear equation is an equation in which all variables are raised to only the 1st power. In this section, we review the algebra of solving basic linear equations, see how these skills can be used in applied settings, look at linear equations with more than one variable, and then use this to find inverse functions of a linear function. Basic Linear Equations To solve a basic linear equation in one variable we use the basic operations of +, -, ´, ¸ to isolate the variable. Example 1 Solve each of the following: (a) 2x + 4 = 5x -12 (b) 3(2x - 4) = 2(x + 5) Applied Problems Example 2 Company A charges a monthly fee of $5.00 plus 99 cents per download for songs. Company B charges a monthly fee of $7.00 plus 79 cents per download for songs. (a) Give a formula for the monthly cost with each of these companies. (b) For what number of downloads will the monthly cost be the same for both companies? Example 3 A small business is considering hiring a new sales rep. to market its product in a nearby city. Two pay scales are under consideration. Pay Scale 1 Pay the sales rep. a base yearly salary of $10000 plus a commission of 8% of the total yearly sales. Pay Scale 2 Pay the sales rep a base yearly salary of $13000 plus a commission of 6% of the total yearly sales. (a) For each scale above, give a function formula to express the total yearly earnings as a function of the total yearly sales.
    [Show full text]
  • Analysis of XSL Applied to BES
    Analysis of XSL Applied to BES By: Lim Chu Wee, Khoo Khoong Ming. History (2002) Courtois and Pieprzyk announced a plausible attack (XSL) on Rijndael AES. Complexity of ≈ 2225 for AES-256. Later Murphy and Robshaw proposed embedding AES into BES, with equations over F256. S-boxes involved fewer monomials, and would provide a speedup for XSL if it worked (287 for AES-128 in best case). Murphy and Robshaw also believed XSL would not work. (Asiacrypt 2005) Cid and Leurent showed that “compact XSL” does not crack AES. Summary of Our Results We analysed the application of XSL on BES. Concluded: the estimate of 287 was too optimistic; we obtained a complexity ≥ 2401, even if XSL works. Hence it does not crack BES-128. Found further linear dependencies in the expanded equations, upon applying XSL to BES. Similar dependencies exist for AES – unaccounted for in computations of Courtois and Pieprzyk. Open question: does XSL work at all, for some P? Quick Description of AES & BES AES Structure Very general description of AES (in F256): Input: key (k0k1…ks-1), message (M0M1…M15). Suppose we have aux variables: v0, v1, …. At each step we can do one of three things: Let vi be an F2-linear map T of some previously defined byte: one of the vj’s, kj’s or Mj’s. Let vi = XOR of two bytes. Let vi = S(some byte). Here S is given by the map: x → x-1 (S(0)=0). Output = 16 consecutive bytes vi-15…vi-1vi. BES Structure BES writes all equations over F256.
    [Show full text]
  • Algebra 1 WORKBOOK Page #1
    Algebra 1 WORKBOOK Page #1 Algebra 1 WORKBOOK Page #2 Algebra 1 Unit 1: Relationships Between Quantities Concept 1: Units of Measure Graphically and Situationally Lesson A: Dimensional Analysis (A1.U1.C1.A.____.DimensionalAnalysis) Concept 2: Parts of Expressions and Equations Lesson B: Parts of Expressions (A1.U1.C2.B.___.PartsOfExpressions) Concept 3: Perform Polynomial Operations and Closure Lesson C: Polynomial Expressions (A1.U1.C3.C.____.PolynomialExpressions) Lesson D: Add and Subtract Polynomials (A1.U1.C3.D. ____.AddAndSubtractPolynomials) Lesson E: Multiplying Polynomials (A1.U1.C3.E.____.MultiplyingPolynomials) Concept 4: Radicals and Rational and Irrational Number Properties Lesson F: Simplify Radicals (A1.U1.C4.F.___.≅SimplifyRadicals) Lesson G: Radical Operations (A1.U1.C4.G.___.RadicalOperations) Unit 2: Reasoning with Linear Equations and Inequalities Concept 1: Creating and Solving Linear Equations Lesson A: Equations in 1 Variable (A1.U2.C1.A.____.equations) Lesson B: Inequalities in 1 Variable (A1.U2.C1.B.____.inequalities) Lesson C: Rearranging Formulas (Literal Equations) (A1.U2.C1.C.____.literal) Lesson D: Review of Slope and Graphing Linear (A1.U2.C1.D.____.slopegraph) Equations Lesson E:Writing and Graphing Linear Equations (A1.U2.C1.E.____.writingequations) Lesson F: Systems of Equations (A1.U2.C1.F.____.systemsofeq) Lesson G: Graphing Linear Inequalities and Systems of (A1.U2.C1.G.____.systemsofineq) Linear Inequalities Concept 2: Function Overview with Notation Lesson H: Functions and Function Notation (A1.U2.C2.H.___.functions)
    [Show full text]
  • 'Doing and Undoing' Applied to the Action of Exchange Reveals
    mathematics Article How the Theme of ‘Doing and Undoing’ Applied to the Action of Exchange Reveals Overlooked Core Ideas in School Mathematics John Mason 1,2 1 Department of Mathematics and Statistics, Open University, Milton Keynes MK7 6AA, UK; [email protected] 2 Department of Education, University of Oxford, 15 Norham Gardens, Oxford OX2 6PY, UK Abstract: The theme of ‘undoing a doing’ is applied to the ubiquitous action of exchange, showing how exchange pervades a school’s mathematics curriculum. It is possible that many obstacles encountered in school mathematics arise from an impoverished sense of exchange, for learners and possibly for teachers. The approach is phenomenological, in that the reader is urged to undertake the tasks themselves, so that the pedagogical and mathematical comments, and elaborations, may connect directly to immediate experience. Keywords: doing and undoing; exchange; substitution 1. Introduction Arithmetic is seen here as the study of actions (usually by numbers) on numbers, whereas calculation is an epiphenomenon: useful as a skill, but only to facilitate recognition Citation: Mason, J. How the Theme of relationships between numbers. Particular relationships may, upon articulation and of ‘Doing and Undoing’ Applied to analysis (generalisation), turn out to be properties that hold more generally. This way of the Action of Exchange Reveals thinking sets the scene for the pervasive mathematical theme of inverse, also known as Overlooked Core Ideas in School doing and undoing (Gardiner [1,2]; Mason [3]; SMP [4]). Exploiting this theme brings to Mathematics. Mathematics 2021, 9, the surface core ideas, such as exchange, which, although appearing sporadically in most 1530.
    [Show full text]
  • Section 3: Linear Functions
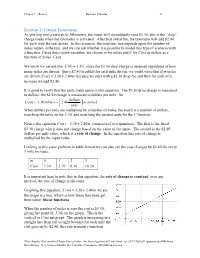
    Chapter 1 Review Business Calculus 31 Section 3: Linear Functions As you hop into a taxicab in Allentown, the meter will immediately read $3.30; this is the “drop” charge made when the taximeter is activated. After that initial fee, the taximeter will add $2.40 for each mile the taxi drives. In this scenario, the total taxi fare depends upon the number of miles ridden in the taxi, and we can ask whether it is possible to model this type of scenario with a function. Using descriptive variables, we choose m for miles and C for Cost in dollars as a function of miles: C(m). We know for certain that C(0) = 3.30 , since the $3.30 drop charge is assessed regardless of how many miles are driven. Since $2.40 is added for each mile driven, we could write that if m miles are driven, C(m) = 3.30 + 2.40m because we start with a $3.30 drop fee and then for each mile increase we add $2.40. It is good to verify that the units make sense in this equation. The $3.30 drop charge is measured in dollars; the $2.40 charge is measured in dollars per mile. So dollars C(m) = 3.30dollars + 2.40 (m miles) mile When dollars per mile are multiplied by a number of miles, the result is a number of dollars, matching the units on the 3.30, and matching the desired units for the C function. Notice this equation C(m) = 3.30 + 2.40m consisted of two quantities.
    [Show full text]