Magnetic Field Outside an Ideal Solenoid—C.E
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Electromagnetic Induction, Ac Circuits, and Electrical Technologies 813
CHAPTER 23 | ELECTROMAGNETIC INDUCTION, AC CIRCUITS, AND ELECTRICAL TECHNOLOGIES 813 23 ELECTROMAGNETIC INDUCTION, AC CIRCUITS, AND ELECTRICAL TECHNOLOGIES Figure 23.1 This wind turbine in the Thames Estuary in the UK is an example of induction at work. Wind pushes the blades of the turbine, spinning a shaft attached to magnets. The magnets spin around a conductive coil, inducing an electric current in the coil, and eventually feeding the electrical grid. (credit: phault, Flickr) 814 CHAPTER 23 | ELECTROMAGNETIC INDUCTION, AC CIRCUITS, AND ELECTRICAL TECHNOLOGIES Learning Objectives 23.1. Induced Emf and Magnetic Flux • Calculate the flux of a uniform magnetic field through a loop of arbitrary orientation. • Describe methods to produce an electromotive force (emf) with a magnetic field or magnet and a loop of wire. 23.2. Faraday’s Law of Induction: Lenz’s Law • Calculate emf, current, and magnetic fields using Faraday’s Law. • Explain the physical results of Lenz’s Law 23.3. Motional Emf • Calculate emf, force, magnetic field, and work due to the motion of an object in a magnetic field. 23.4. Eddy Currents and Magnetic Damping • Explain the magnitude and direction of an induced eddy current, and the effect this will have on the object it is induced in. • Describe several applications of magnetic damping. 23.5. Electric Generators • Calculate the emf induced in a generator. • Calculate the peak emf which can be induced in a particular generator system. 23.6. Back Emf • Explain what back emf is and how it is induced. 23.7. Transformers • Explain how a transformer works. • Calculate voltage, current, and/or number of turns given the other quantities. -

Magnetic Fields
Welcome Back to Physics 1308 Magnetic Fields Sir Joseph John Thomson 18 December 1856 – 30 August 1940 Physics 1308: General Physics II - Professor Jodi Cooley Announcements • Assignments for Tuesday, October 30th: - Reading: Chapter 29.1 - 29.3 - Watch Videos: - https://youtu.be/5Dyfr9QQOkE — Lecture 17 - The Biot-Savart Law - https://youtu.be/0hDdcXrrn94 — Lecture 17 - The Solenoid • Homework 9 Assigned - due before class on Tuesday, October 30th. Physics 1308: General Physics II - Professor Jodi Cooley Physics 1308: General Physics II - Professor Jodi Cooley Review Question 1 Consider the two rectangular areas shown with a point P located at the midpoint between the two areas. The rectangular area on the left contains a bar magnet with the south pole near point P. The rectangle on the right is initially empty. How will the magnetic field at P change, if at all, when a second bar magnet is placed on the right rectangle with its north pole near point P? A) The direction of the magnetic field will not change, but its magnitude will decrease. B) The direction of the magnetic field will not change, but its magnitude will increase. C) The magnetic field at P will be zero tesla. D) The direction of the magnetic field will change and its magnitude will increase. E) The direction of the magnetic field will change and its magnitude will decrease. Physics 1308: General Physics II - Professor Jodi Cooley Review Question 2 An electron traveling due east in a region that contains only a magnetic field experiences a vertically downward force, toward the surface of the earth. -

Transformed E&M I Homework Magnetic Vector Potential
Transformed E&M I homework Magnetic Vector Potential (Griffiths Chapter 5) Magnetic Vector Potential A Question 1. Vector potential inside current-carrying conductor Lorrain, Dorson, Lorrain, 15-1 pg. 272 Show that, inside a straight current-carrying conductor of radius R, µ Ι ρ 2 Α = 0 (1− ) 2π R 2 If A is set equal to zero at ρ = R. Question 2. Multipoles, dipole moment The vector potential of a small current loop (a magnetic dipole) with magnetic moment µ0 m × rˆ m is A = 2 4π r A) Assume that the magnetic dipole is at the origin and the magnetic moment is aligned with the +z axis. Use the vector potential to compute the B-field in spherical coordinates. B) Show that your expression for the B-field in part (a) can be written in the coordinate- € µ 1 0 ˆ ˆ free form B(r) = 3 3(m⋅r)r − m 4π r Note: The easiest way to do this one is by assuming the coordinate-free form and then showing that you get your expression in part (a) if you define your z axis to lie along m, rather than trying to go the other way around. Coordinate free formulas are nice, because now you can find B for more general situations. Question 3. Vector Potential of infinite sheet Lorrain, Dorson; Example, Pair of Long Parallel Currents pg. 252 Figure 14-10 shows two long parallel wires separated by a distance D and carrying equal currents I in opposite directions. To calculate A, we use the above result for the A of a single wire and add the two vector potentials: µ Ι L L A = 0 (ln − ln ) (14-37) 2π ρ a ρb Do Bx, By, and Bz at midpoint stretch? Question 4. -

Design and Optimization of Printed Circuit Board Inductors for Wireless Power Transfer System
University of Tennessee, Knoxville TRACE: Tennessee Research and Creative Exchange Engineering -- Faculty Publications and Other Faculty Publications and Other Works -- EECS Works 4-2013 Design and Optimization of Printed Circuit Board Inductors for Wireless Power Transfer System Ashraf B. Islam University of Tennessee - Knoxville Syed K. Islam University of Tennessee - Knoxville Fahmida S. Tulip Follow this and additional works at: https://trace.tennessee.edu/utk_elecpubs Part of the Electrical and Computer Engineering Commons Recommended Citation Islam, Ashraf B.; Islam, Syed K.; and Tulip, Fahmida S., "Design and Optimization of Printed Circuit Board Inductors for Wireless Power Transfer System" (2013). Faculty Publications and Other Works -- EECS. https://trace.tennessee.edu/utk_elecpubs/21 This Article is brought to you for free and open access by the Engineering -- Faculty Publications and Other Works at TRACE: Tennessee Research and Creative Exchange. It has been accepted for inclusion in Faculty Publications and Other Works -- EECS by an authorized administrator of TRACE: Tennessee Research and Creative Exchange. For more information, please contact [email protected]. Circuits and Systems, 2013, 4, 237-244 http://dx.doi.org/10.4236/cs.2013.42032 Published Online April 2013 (http://www.scirp.org/journal/cs) Design and Optimization of Printed Circuit Board Inductors for Wireless Power Transfer System Ashraf B. Islam, Syed K. Islam, Fahmida S. Tulip Department of Electrical Engineering and Computer Science, University of Tennessee, Knoxville, USA Email: [email protected] Received November 20, 2012; revised December 20, 2012; accepted December 27, 2012 Copyright © 2013 Ashraf B. Islam et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. -

THP40 Proceedings of the 12Th International Workshop on RF Superconductivity, Cornell University, Ithaca, New York, USA Cavity Region Is Less Than 40 Mt
Proceedings of the 12th International Workshop on RF Superconductivity, Cornell University, Ithaca, New York, USA Magnetic Field Studies in the ISAC-II Cryomodule R.E Laxdal, B. Boussier, K. Fong, I. Sekachev, G. Clark, V. Zvyagintsev, TRIUMF∗, Vancouver, BC, V6T2A3, Canada, R. Eichhorn, FZ-Juelich, Germany Abstract The medium beta section of the ISAC-II Heavy Ion Ac- celerator consists of five cryomodules each containing four quarter wave bulk niobium resonators and one supercon- ducting solenoid. The 9 T solenoid is not shielded but is equipped with bucking coils to reduce the magnetic field in the neighbouring rf cavities. A prototype cryomodule has been designed and assembled at TRIUMF. The cryomod- ule vacuum space shares the cavity vacuum and contains a mu-metal shield, an LN2 cooled, copper, thermal shield, plus the cold mass and support system. Several cold tests have been done to characterize the cryomodule. Early op- erating experience with a high field solenoid inside a cry- omodule containing SRF cavities will be given. The re- sults include measurements of the passive magnetic field in the cryomodule. We also estimate changes in the magnetic Figure 1: Cryomodule top assembly in the assembly frame field during the test due to trapped flux in the solenoid. prior to the cold test. Residual field reduction due to hysteresis cycling of the solenoid has been demonstrated. ISAC-II CAVITIES INTRODUCTION The ISAC-II medium beta cavity design goal is to op- erate up to 6 MV/m across an 18 cm effective length with TRIUMF is now preparing a new heavy ion supercon- Pcav ≤ 7 W. -

Coil Inductance Model Based Solenoid On–Off Valve Spool Displacement Sensing Via Laser Calibration
sensors Article Coil Inductance Model Based Solenoid on–off Valve Spool Displacement Sensing via Laser Calibration Hao Tian * and Yuren Zhao Department of Mechanical Engineering, Dalian Maritime University, Dalian 116026, China; [email protected] * Correspondence: [email protected]; Tel.: +86-0411-8472-5229 Received: 20 October 2018; Accepted: 17 December 2018; Published: 18 December 2018 Abstract: Direct acting solenoid on–off valves are key fluid power components whose efficiency is dependent upon the state of the spool’s axial motion. By sensing the trajectory of the valve spool, more efficient control schemes can be implemented. Therefore, the goal of this study is to derive an analytical model for spool displacement sensing based on coil inductance. First, a mathematical model of the coil inductance as a function of air gap width and lumped magnetic reluctance is derived. Second, to solve the inductance from coil current, an optimization to obtain an initial value based on physical constraints is proposed. Furthermore, an experiment using a laser triangulation sensor is designed to correlate the magnetic reluctance to the air gap. Lastly, using the obtained empirical reluctance model to eliminate unknowns from the proposed air gap-inductance model, the model in atmosphere or hydraulic oil environments was tested. Initial results showed that the proposed model is capable of calculating the spool displacement based on the coil current, and the estimation errors compared to the laser measurement are within ±7% in air environment. Keywords: on–off solenoid; air gap; spool displacement sensing; solenoid inductance; laser triangulation sensor 1. Introduction Solenoid on–off valves are key control elements in a fluid power system. -

Directional Characteristics of Wireless Power Transfer Via Coupled Magnetic Resonance
electronics Article Directional Characteristics of Wireless Power Transfer via Coupled Magnetic Resonance Yang Li, Jiaming Liu *, Qingxin Yang, Xin Ni, Yujie Zhai and Zhigang Lou Tianjin Key Laboratory of Advanced Electrical Engineering and Energy Technology, Tiangong University, Tianjin 300387, China; [email protected] (Y.L.); [email protected] (Q.Y.); [email protected] (X.N.); [email protected] (Y.Z.); [email protected] (Z.L.) * Correspondence: [email protected]; Tel.: +86-18622851377 Received: 11 October 2020; Accepted: 10 November 2020; Published: 13 November 2020 Abstract: The wireless power transfer (WPT) system via coupled magnetic resonance (CMR) is an efficient and practical power transmission technology that can realize medium- and long-distance power transmission. People’s requirements for the flexibility of charging equipment are becoming increasingly prominent. How to get rid of the “flitch plate type” wireless charging method and enhance the anti-offset performance is the main research direction. Directional characteristics of the system can affect the load receive power and system efficiency in practical applications. In this paper, the power and efficiency of the WPT system via CMR were analyzed according to the principle of near-field strong coupling at first. The expression of the mutual inductance between the transmitting and the receiving coils under angular offset was derived from the perspective of the mathematical model, and the influences of angular deviation were analyzed. Second, simulation models were established under different distance between coils, different coil types, and different coil radius ratios in symmetrical and asymmetrical systems. Afterwards, the directional law was obtained, providing reference for the optimal design of coupling coils. -

1 CHAPTER 9 MAGNETIC POTENTIAL 9.1 Introduction We Are Familiar with the Idea That an Electric Field E Can Be Expressed As
1 CHAPTER 9 MAGNETIC POTENTIAL 9.1 Introduction We are familiar with the idea that an electric field E can be expressed as minus the gradient of a potential function V. That is E = −grad V = −===V. 9.1.1 Note that V is not unique, because an arbitrary constant can be added to it. We can define a unique V by assigning a particular value of V to some point (such as zero at infinity). Can we express the magnetic field B in a similar manner as the gradient of some potential function ψ, so that, for example, B = −grad ψ = − ===ψ ? Before answering this, we note that there are some differences between E and B . Unlike E, the magnetic field B is sourceless ; there are no sources or sinks; the magnetic field lines are closed loops. The force on a charge q in an electric field is qE, and it depends only on where the charge is in the electric field – i.e. on its position. Thus the force is conservative , and we understand from any study of classical mechanics that only conservative forces can be expressed as the derivative of a potential function. The force on a charge q in a magnetic field is qv %%% B . This force (the Lorentz force) does not depend only on the position of the particle, but also on its velocity (speed and direction). Thus the force is not conservative. This suggests that perhaps we cannot express the magnetic field merely as the gradient of a scalar potential function – and this is correct; we cannot. -

Arxiv:Physics/0611099V1
Derivation of magnetic Coulomb’s law for thin, semi-infinite solenoids Masao Kitano∗ Department of Electronic Science and Engineering, Kyoto University, Katsura, Kyoto 615-8510, Japan and CREST, Japan Science and Technology Agency, Tokyo 103-0028, Japan (Dated: February 2, 2008) It is shown that the magnetic force between thin, semi-infinite solenoids obeys a Coulomb-type law, which corresponds to that for magnetic monopoles placed at the end points of each solenoid. We derive the magnetic Coulomb law from the basic principles of electromagnetism, namely from the Maxwell equations and the Lorentz force. I. INTRODUCTION from Maxwell’s equations and the Lorentz force, none of which contain the notion of magnetic monopoles. The derivation of magnetic Coulomb’s law was given A permanent magnet is an ensemble of microscopic 3 4 magnetic moments which are oriented along the magne- more than forty years ago by Chen and Nadeau . In tization direction. A magnetic moment can be modeled this paper a more detailed analysis based directly on the as a dipole, i.e., as a slightly displaced pair of magnetic fundamental laws will be provided. The field singularity monopoles with opposite polarities. It is analogous to the for infinitesimal loop currents, which plays crucial roles electric dipole. Another way of modeling is to consider but was not mentioned in the previous works, will be each magnetic moment as a circulating current loop. In treated rigorously. terms of far fields, the dipole model and the loop-current model give exactly the same magnetic field. The lat- ter model is more natural because there are no magnetic II. -

Chapter 10 Superconducting Solenoid Magnets
Chapter 10 Superconducting Solenoid Magnets 10.1 Introduction The Neutrino Factory [1], [2], [3], beyond approximately 18 m from the target, requires three solenoid-based magnetic channels. In total, more than 530 m of solenoids with di®erent magnetic strengths and bore sizes are used in order to prepare the muon beam for injection into the muon acceleration system. This is followed by the pre-acceleration linac with several di®erent low-stray-¯eld solenoids. 10.2 Decay and Phase Rotation Channel Solenoids The decay and phase rotation region includes the muon decay channel, an induction linac (IL1), the mini-cooler and two additional induction linacs (IL2, IL3). This region extends from z = 18 m (from the target) to z = 356 m; within it, there are four types of solenoids. From z = 18 m to z = 36 m, the decay section has a warm bore diameter of 600 mm. ² Around this warm bore is a water-cooled copper shield that is 100 mm thick. The solenoid cryostat warm bore is 800 mm. The 18 m of decay solenoid is divided into six cryostats, each 2.9-m long. This same type of magnet is used for the 9-m long mini-cooling sections on either side of the field-flip solenoid. As a result, there are twelve magnets of this type. The IL1 solenoids, which extend from z = 36 m to z = 146 m, have a beam ² aperture of 600 mm diameter. Around the bore is a 10-mm-thick water-cooled copper radiation shield. The warm bore of this magnet cryostat is 620 mm in diameter. -

Inductance Inductance
Inductance Important fact: Magnetic Flux ΦB is proportional to the current making the ΦB All our equations for B-fields show that B α I v v v v µ0 I dl × rˆ dB = ∫ B ⋅dl = µ0Ithru 4π r2 Biot-Savart Ampere Inductance Flux Φ B ∝ B ∝ I Flux Φ ∝ I Assumes leaving everything else B the same. If we double the current I, we will double the magnetic flux through any surface. i 1 Self-inductance Self-Inductance (L) of a coil of wire ΦB ≡ LI Φ This equation defines self-inductance. L B ≡ Note that since ΦB α I, L must be I independent of the current I. L has units [L] = [Tesla meter2]/[Amperes] New unit for inductance = [Henry]. Inductors (coil of wire) An inductor is just a coil of wire. The Magnetic Flux created by the coil, through the coil itself: v v Φ B = ∫ B ⋅dA This is quite hard to calculate for a single loop. Earlier we calculated B at the center, but it varies over the area. 2 Inductors Consider a simpler case of a solenoid v N | B |= µ nI = µ I inside 0 0 L Recall that the B-field inside a solenoid is uniform! N = number of loops L = length of solenoid * Be careful with symbol L ! Inductors v N | B |= µ nI = µ I inside 0 0 L v v Φ B = N ∫ B ⋅ dA = NBA = N(µ0nI)A Φ L = B = µ NnA = µ An2L I 0 0 Self-Inductance Length 3 Clicker Question Inductor 1 consists of a single loop of wire. -
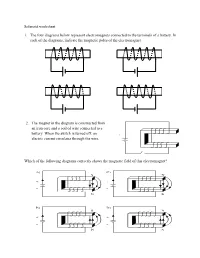
Solenoid Practice
Solenoid worksheet 1. The four diagrams below represent electromagnets connected to the terminals of a battery. In each of the diagrams, indicate the magnetic poles of the electromagnet 2. The magnet in the diagram is constructed from an iron core and a coil of wire connected to a battery. When the switch is turned off, an + electric current circulates through the wire. − Which of the following diagrams correctly shows the magnetic field of this electromagnet? A) C) S N + + − − N S B) D) S N + + − − N S 3. Two of the following diagrams correctly represent the magnetic field created by an electric current flowing through a solenoid. Which two diagrams are they? - + 1. - + 3. I I 2. 4. I I 4. In the solenoid below, which terminal (A or B) of the power supply is positive, and which is negative? 5. An electric current flows through a solenoid. Which diagram correctly illustrates the magnetic field produced by this solenoid? 6. A bar magnet is brought close to a current-bearing electromagnet. Indicate whether there will be attraction or repulsion between the electromagnet and the bar magnet. a) S N b) S N + − − + c) d) S N N S + − − + 7. Which of the following diagrams correctly represents the magnetic lines of force between two solenoids? A B C D 8. On each diagram, draw the magnetic lines of force that are present and indicate the magnetic poles when a current flows through the two solenoids. electron flow electron flow 9. Electric current flows through three solenoids aligned side by side. Solenoid 1 Solenoid 2 Solenoid 3 Determine if there will be attraction or repulsion between the three solenoids.