DOCSLIB.ORG

Critical Points. Local Maxima and Minima

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Critical Points. Local Maxima and Minima Calculus and Vectors – How to get an A+ 4.2 Critical Points. Local Maxima and Minima A Local Maximum B Local Minimum A function f has a local (relative) maximum at x = c if A function f has a local (relative) minimum at x = c if f (x) ≤ f (c) when x is sufficiently close to c (from both f (x) ≥ f (c) when x is sufficiently close to c (from both sides). sides). f (c) is called the local (relative) maximum value. f (c) is called the local (relative) minimum value. (c, f (c)) is called the local (relative) maximum point. (c, f (c)) is called the local (relative) minimum point. C Note Ex 1. A function is defined by the following graph. Find the local minimum or maximum points. The following points are neither local minimum or maximum points. Local minimum points are A(−5,2) , B(−1,1) , and C(5,2) . Local maximum points are D(−2,4) and E(2,5) . D Critical Numbers and Critical Points Ex 2. Find the critical points for: 3 2 The number c ∈ D f is a critical number if either a) f (x) = 2x + 3x f '(c) = 0 or f '(c) DNE f '(x) = 6x2 + 6x = 6x(x +1) The point P(c, f (c)) is called critical point. f '(x) = 0 ⇒ x = 0 or x = −1 f (0) = 0 f (−1) = 2(−1)3 + 3(−1)2 = −2 + 3 =1 The critical points are A(0,0) and B(−1,1) . b) f (x) = 3 x2 −1 ' 1 2x f '(x) = [(x2 −1)1/3 ] = (x2 −1)−2/3 (2x) = 3 3 3 (x2 −1)2 f '(x) = 0 ⇒ x = 0, y = −1 f '(x) DNE ⇒ x2 −1 = 0 ⇒ x = ±1, y = 0 The critical points are A(0,−1) , B(−1,0) , and C(1,0) . 4.2 Critical Points. Local Maxima and Minima ©2010 Iulia & Teodoru Gugoiu - Page 1 of 2 Calculus and Vectors – How to get an A+ E Fermat’s Theorem Note. If f has a local extremum (minimum or maximum) at If x = c then c is a critical number for f . So, at a local f '(c) = 0 or f '(c) DNE extremum: then the function f may have or not a local extremum f '(c) = 0 or f '(c) DNE (minimum or maximum) at x = c . F First Derivative Test Ex 3. Find the local extrema points for the functions in Let c be a critical number of a continuous function f . the previous example. If f '(x) changes sign from positive to negative at 3 2 c then f has a local maximum at c . a) f (x) = 2x + 3x f '(x) = 6x2 + 6x = 6x(x +1) Sign Chart: x −1 0 f (x) _ 1 ` 0 _ f '(x) + 0 - 0 + If f '(x) changes sign from negative to positive at The point A(0,0) is a local minimum point and the point c then f has a local minimum at c . B(−1,1) is a local maximum point. b) f (x) = 3 x2 −1 2x f '(x) = 3 3 (x2 −1)2 Sign Chart: If f '(x) does not change sign at c then f has no local extremum (minimum or maximum) at c . x −1 0 1 f (x) ` 0 ` −1 _ 0 _ f '(x) - DNE - 0 + DNE + The point A(0,−1) is a local minimum point. Ex 4. Find a function of the form f (x) = ax4 + bx2 + cx + d with a local maximum at (0,−6) and a local minimum at (1,−8) . f (0) = −6 ⇒ d = −6 (1) f (1) = −8 ⇒ a + b + c + d = −8 (2) f '(x) = 4ax3 + 2bx + c f '(0) = 0 ⇒ c = 0 (3) f '(1) = 0 ⇒ 4a + 2b + c = 0 (4) ⎧a + b + 0 − 6 = −8 ⎧a + b = −2 (1),(2),(3),(4) ⇒ ⎨ ⇒ ⎨ ⇒ ⎩4a + 2b + 0 = 0 ⎩2a + b = 0 a = 2 and b = −4 ∴ f (x) = 2x4 − 4x2 − 6 Reading: Nelson Textbook, Pages 172-178 Homework: Nelson Textbook: Page 178 #3ab, 5ad, 7adf, 10, 13, 15 4.2 Critical Points. Local Maxima and Minima ©2010 Iulia & Teodoru Gugoiu - Page 2 of 2 .
Load more

Recommended publications
  • Optimization and Gradient Descent INFO-4604, Applied Machine Learning University of Colorado Boulder
    Optimization and Gradient Descent INFO-4604, Applied Machine Learning University of Colorado Boulder September 11, 2018 Prof. Michael Paul Prediction Functions Remember: a prediction function is the function that predicts what the output should be, given the input. Prediction Functions Linear regression: f(x) = wTx + b Linear classification (perceptron): f(x) = 1, wTx + b ≥ 0 -1, wTx + b < 0 Need to learn what w should be! Learning Parameters Goal is to learn to minimize error • Ideally: true error • Instead: training error The loss function gives the training error when using parameters w, denoted L(w). • Also called cost function • More general: objective function (in general objective could be to minimize or maximize; with loss/cost functions, we want to minimize) Learning Parameters Goal is to minimize loss function. How do we minimize a function? Let’s review some math. Rate of Change The slope of a line is also called the rate of change of the line. y = ½x + 1 “rise” “run” Rate of Change For nonlinear functions, the “rise over run” formula gives you the average rate of change between two points Average slope from x=-1 to x=0 is: 2 f(x) = x -1 Rate of Change There is also a concept of rate of change at individual points (rather than two points) Slope at x=-1 is: f(x) = x2 -2 Rate of Change The slope at a point is called the derivative at that point Intuition: f(x) = x2 Measure the slope between two points that are really close together Rate of Change The slope at a point is called the derivative at that point Intuition: Measure the
    [Show full text]
  • Maxima and Minima
    Basic Mathematics Maxima and Minima R Horan & M Lavelle The aim of this document is to provide a short, self assessment programme for students who wish to be able to use differentiation to find maxima and mininima of functions. Copyright c 2004 [email protected] , [email protected] Last Revision Date: May 5, 2005 Version 1.0 Table of Contents 1. Rules of Differentiation 2. Derivatives of order 2 (and higher) 3. Maxima and Minima 4. Quiz on Max and Min Solutions to Exercises Solutions to Quizzes Section 1: Rules of Differentiation 3 1. Rules of Differentiation Throughout this package the following rules of differentiation will be assumed. (In the table of derivatives below, a is an arbitrary, non-zero constant.) y axn sin(ax) cos(ax) eax ln(ax) dy 1 naxn−1 a cos(ax) −a sin(ax) aeax dx x If a is any constant and u, v are two functions of x, then d du dv (u + v) = + dx dx dx d du (au) = a dx dx Section 1: Rules of Differentiation 4 The stationary points of a function are those points where the gradient of the tangent (the derivative of the function) is zero. Example 1 Find the stationary points of the functions (a) f(x) = 3x2 + 2x − 9 , (b) f(x) = x3 − 6x2 + 9x − 2 . Solution dy (a) If y = 3x2 + 2x − 9 then = 3 × 2x2−1 + 2 = 6x + 2. dx The stationary points are found by solving the equation dy = 6x + 2 = 0 . dx In this case there is only one solution, x = −1/3.
    [Show full text]
  • Calculus 120, Section 7.3 Maxima & Minima of Multivariable Functions
    Calculus 120, section 7.3 Maxima & Minima of Multivariable Functions notes by Tim Pilachowski A quick note to start: If you’re at all unsure about the material from 7.1 and 7.2, now is the time to go back to review it, and get some help if necessary. You’ll need all of it for the next three sections. Just like we had a first-derivative test and a second-derivative test to maxima and minima of functions of one variable, we’ll use versions of first partial and second partial derivatives to determine maxima and minima of functions of more than one variable. The first derivative test for functions of more than one variable looks very much like the first derivative test we have already used: If f(x, y, z) has a relative maximum or minimum at a point ( a, b, c) then all partial derivatives will equal 0 at that point. That is ∂f ∂f ∂f ()a b,, c = 0 ()a b,, c = 0 ()a b,, c = 0 ∂x ∂y ∂z Example A: Find the possible values of x, y, and z at which (xf y,, z) = x2 + 2y3 + 3z 2 + 4x − 6y + 9 has a relative maximum or minimum. Answers : (–2, –1, 0); (–2, 1, 0) Example B: Find the possible values of x and y at which fxy(),= x2 + 4 xyy + 2 − 12 y has a relative maximum or minimum. Answer : (4, –2); z = 12 Notice that the example above asked for possible values. The first derivative test by itself is inconclusive. The second derivative test for functions of more than one variable is a good bit more complicated than the one used for functions of one variable.
    [Show full text]
  • Mean Value, Taylor, and All That
    Mean Value, Taylor, and all that Ambar N. Sengupta Louisiana State University November 2009 Careful: Not proofread! Derivative Recall the definition of the derivative of a function f at a point p: f (w) − f (p) f 0(p) = lim (1) w!p w − p Derivative Thus, to say that f 0(p) = 3 means that if we take any neighborhood U of 3, say the interval (1; 5), then the ratio f (w) − f (p) w − p falls inside U when w is close enough to p, i.e. in some neighborhood of p. (Of course, we can’t let w be equal to p, because of the w − p in the denominator.) In particular, f (w) − f (p) > 0 if w is close enough to p, but 6= p. w − p Derivative So if f 0(p) = 3 then the ratio f (w) − f (p) w − p lies in (1; 5) when w is close enough to p, i.e. in some neighborhood of p, but not equal to p. Derivative So if f 0(p) = 3 then the ratio f (w) − f (p) w − p lies in (1; 5) when w is close enough to p, i.e. in some neighborhood of p, but not equal to p. In particular, f (w) − f (p) > 0 if w is close enough to p, but 6= p. w − p • when w > p, but near p, the value f (w) is > f (p). • when w < p, but near p, the value f (w) is < f (p). Derivative From f 0(p) = 3 we found that f (w) − f (p) > 0 if w is close enough to p, but 6= p.
    [Show full text]
  • Math 105: Multivariable Calculus Seventeenth Lecture (3/17/10)
    Daily Summary Fast Taylor Series Critical Points and Extrema Lagrange Multipliers Math 105: Multivariable Calculus Seventeenth Lecture (3/17/10) Steven J Miller Williams College [email protected] http://www.williams.edu/go/math/sjmiller/ public html/341/ Bronfman Science Center Williams College, March 17, 2010 1 Daily Summary Fast Taylor Series Critical Points and Extrema Lagrange Multipliers Summary for the Day 2 Daily Summary Fast Taylor Series Critical Points and Extrema Lagrange Multipliers Summary for the day Fast Taylor Series. Critical Points and Extrema. Constrained Maxima and Minima. 3 Daily Summary Fast Taylor Series Critical Points and Extrema Lagrange Multipliers Fast Taylor Series 4 Daily Summary Fast Taylor Series Critical Points and Extrema Lagrange Multipliers Formula for Taylor Series Notation: f twice differentiable function ∂f ∂f Gradient: f =( ∂ ,..., ∂ ). ∇ x1 xn Hessian: ∂2f ∂2f ∂x1∂x1 ∂x1∂xn . ⋅⋅⋅. Hf = ⎛ . .. ⎞ . ∂2f ∂2f ⎜ ∂ ∂ ∂ ∂ ⎟ ⎝ xn x1 ⋅⋅⋅ xn xn ⎠ Second Order Taylor Expansion at −→x 0 1 T f (−→x 0) + ( f )(−→x 0) (−→x −→x 0)+ (−→x −→x 0) (Hf )(−→x 0)(−→x −→x 0) ∇ ⋅ − 2 − − T where (−→x −→x 0) is the row vector which is the transpose of −→x −→x 0. − − 5 Daily Summary Fast Taylor Series Critical Points and Extrema Lagrange Multipliers Example 3 Let f (x, y)= sin(x + y) + (x + 1) y and (x0, y0) = (0, 0). Then ( f )(x, y) = cos(x + y)+ 3(x + 1)2y, cos(x + y) + (x + 1)3 ∇ and sin(x + y)+ 6(x + 1)2y sin(x + y)+ 3(x + 1)2 (Hf )(x, y) = − − , sin(x + y)+ 3(x + 1)2 sin(x + y) − − so 0 3 f (0, 0)= 0, ( f )(0, 0) = (1, 2), (Hf )(0, 0)= ∇ 3 0 which implies the second order Taylor expansion is 1 0 3 x 0 + (1, 2) (x, y)+ (x, y) ⋅ 2 3 0 y 1 3y = x + 2y + (x, y) = x + 2y + 3xy.
    [Show full text]
  • Lecture 13: Extrema
    Math S21a: Multivariable calculus Oliver Knill, Summer 2013 Lecture 13: Extrema An important problem in multi-variable calculus is to extremize a function f(x, y) of two vari- ables. As in one dimensions, in order to look for maxima or minima, we consider points, where the ”derivative” is zero. A point (a, b) in the plane is called a critical point of a function f(x, y) if ∇f(a, b) = h0, 0i. Critical points are candidates for extrema because at critical points, all directional derivatives D~vf = ∇f · ~v are zero. We can not increase the value of f by moving into any direction. This definition does not include points, where f or its derivative is not defined. We usually assume that a function is arbitrarily often differentiable. Points where the function has no derivatives are not considered part of the domain and need to be studied separately. For the function f(x, y) = |xy| for example, we would have to look at the points on the coordinate axes separately. 1 Find the critical points of f(x, y) = x4 + y4 − 4xy + 2. The gradient is ∇f(x, y) = h4(x3 − y), 4(y3 − x)i with critical points (0, 0), (1, 1), (−1, −1). 2 f(x, y) = sin(x2 + y) + y. The gradient is ∇f(x, y) = h2x cos(x2 + y), cos(x2 + y) + 1i. For a critical points, we must have x = 0 and cos(y) + 1 = 0 which means π + k2π. The critical points are at ... (0, −π), (0, π), (0, 3π),.... 2 2 3 The graph of f(x, y) = (x2 + y2)e−x −y looks like a volcano.
    [Show full text]
  • Some Recent Developments in the Calculus of Variations.*
    1920.] THE CALCULUS OF VARIATIONS. 343 SOME RECENT DEVELOPMENTS IN THE CALCULUS OF VARIATIONS.* BY PROFESSOR GILBERT AMES BLISS. IT is my purpose to speak this afternoon of a part of the theory of the calculus of variations which has aroused the interest and taxed the ingenuity of a sequence of mathe­ maticians beginning with Legendre, and extending by way of Jacobi, Clebsch, Weierstrass, and a numerous array of others, to the present time. The literature of the subject is very large and is still growing. I was discussing recently the title of this address with a fellow mathematician who remarked that he was not aware that there had been any recent progress in the calculus of variations. This was a very natural sus­ picion, I think, in view of the fact that the attention of most mathematicians of the present time seems irresistibly attracted to such subjects as integral equations and their generaliza­ tions, the theory of definite integration, and the theory of functions of lines. It is indeed in these latter domains that the activities especially characteristic of the present era are centered, and the progress already made in them, and the further progress inevitable in the near future, will doubtless be sufficient alone to insure for our generation of mathematical workers a noteworthy place in the history of the science. While speaking of present day mathematical tendencies I should like to take occasion to mention a remark which has been made to me a number of times by persons who are inter­ ested in mathematics primarily for its applications.
    [Show full text]
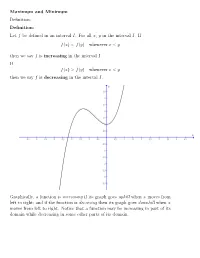
  • Maximum and Minimum Definition
    Maximum and Minimum Definition: Definition: Let f be defined in an interval I. For all x, y in the interval I. If f(x) < f(y) whenever x < y then we say f is increasing in the interval I. If f(x) > f(y) whenever x < y then we say f is decreasing in the interval I. Graphically, a function is increasing if its graph goes uphill when x moves from left to right; and if the function is decresing then its graph goes downhill when x moves from left to right. Notice that a function may be increasing in part of its domain while decreasing in some other parts of its domain. For example, consider f(x) = x2. Notice that the graph of f goes downhill before x = 0 and it goes uphill after x = 0. So f(x) = x2 is decreasing on the interval (−∞; 0) and increasing on the interval (0; 1). Consider f(x) = sin x. π π 3π 5π 7π 9π f is increasing on the intervals (− 2 ; 2 ), ( 2 ; 2 ), ( 2 ; 2 )...etc, while it is de- π 3π 5π 7π 9π 11π creasing on the intervals ( 2 ; 2 ), ( 2 ; 2 ), ( 2 ; 2 )...etc. In general, f = sin x is (2n+1)π (2n+3)π increasing on any interval of the form ( 2 ; 2 ), where n is an odd integer. (2m+1)π (2m+3)π f(x) = sin x is decreasing on any interval of the form ( 2 ; 2 ), where m is an even integer. What about a constant function? Is a constant function an increasing function or decreasing function? Well, it is like asking when you walking on a flat road, as you going uphill or downhill? From our definition, a constant function is neither increasing nor decreasing.
    [Show full text]
  • Chapter 11 Maxima and Minima in One Variable
    Chapter 11 Maxima and Minima in One Variable Finding a maximum or a minimum clearly is important in everyday experience. A manufacturer wants to maximize her profits, a contractor wants to minimize his costs subject to doing a good job, and a physicist wants to find the wavelength that produces the maximum intensity of radiation. Even a manufacturer with a monopoly cannot maximize her profits by charging a very high price because at some point consumers will stop buying. She seeks an optimal balance between supply and demand. In everyday experience, these optima are sought in intuitive ways, probably incorrectly in many cases. The problems are not usually simple, and often they are not even clearly formulated. Calculus can help. It can solve closed-form problems and offer guidance when the mathematical models are incomplete. Much of the success of science and engineering is based on finding symbolic optima for accurate models, but no one pretends to know closed-form models for the national health profile and similar interesting, but complicated facts of everyday life. This chapter starts with some basic mathematical theory and then looks at some ‘simple’ appli- cations. They are simple in terms of life’s big questions but still offer some challenge mathematically. They may not be major “real world” revelations but are a start and have some practical signifi- cance. We are not retreating from our basic philosophy in this course, which is to show you what good calculus is. We think you know that optimization is important, so we will begin with the easy part: the mathematical theory.
    [Show full text]
  • H. Jerome Keisler : Foundations of Infinitesimal Calculus
    FOUNDATIONS OF INFINITESIMAL CALCULUS H. JEROME KEISLER Department of Mathematics University of Wisconsin, Madison, Wisconsin, USA [email protected] June 4, 2011 ii This work is licensed under the Creative Commons Attribution-Noncommercial- Share Alike 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/ Copyright c 2007 by H. Jerome Keisler CONTENTS Preface................................................................ vii Chapter 1. The Hyperreal Numbers.............................. 1 1A. Structure of the Hyperreal Numbers (x1.4, x1.5) . 1 1B. Standard Parts (x1.6)........................................ 5 1C. Axioms for the Hyperreal Numbers (xEpilogue) . 7 1D. Consequences of the Transfer Axiom . 9 1E. Natural Extensions of Sets . 14 1F. Appendix. Algebra of the Real Numbers . 19 1G. Building the Hyperreal Numbers . 23 Chapter 2. Differentiation........................................ 33 2A. Derivatives (x2.1, x2.2) . 33 2B. Infinitesimal Microscopes and Infinite Telescopes . 35 2C. Properties of Derivatives (x2.3, x2.4) . 38 2D. Chain Rule (x2.6, x2.7). 41 Chapter 3. Continuous Functions ................................ 43 3A. Limits and Continuity (x3.3, x3.4) . 43 3B. Hyperintegers (x3.8) . 47 3C. Properties of Continuous Functions (x3.5{x3.8) . 49 Chapter 4. Integration ............................................ 59 4A. The Definite Integral (x4.1) . 59 4B. Fundamental Theorem of Calculus (x4.2) . 64 4C. Second Fundamental Theorem of Calculus (x4.2) . 67 Chapter 5. Limits ................................................... 71 5A. "; δ Conditions for Limits (x5.8, x5.1) . 71 5B. L'Hospital's Rule (x5.2) . 74 Chapter 6. Applications of the Integral........................ 77 6A. Infinite Sum Theorem (x6.1, x6.2, x6.6) . 77 6B. Lengths of Curves (x6.3, x6.4) .
    [Show full text]
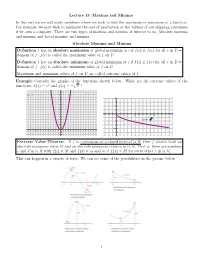
  • Lecture 15 :Maxima and Minima in This Section We Will Study Problems Where We Wish to find the Maximum Or Minimum of a Function
    Lecture 15 :Maxima and Minima In this section we will study problems where we wish to find the maximum or minimum of a function. For example, we may wish to minimize the cost of production or the volume of our shipping containers if we own a company. There are two types of maxima and minima of interest to us, Absolute maxima and minima and Local maxima and minima. Absolute Maxima and Minima Definition f has an absolute maximum or global maximum at c if f(c) ≥ f(x) for all x in D = domain of f. f(c) is called the maximum value of f on D. Definition f has an absolute minimum or global minimum at c if f(c) ≤ f(x) for all x in D = domain of f. f(c) is called the minimum value of f on D.12 24 Maximum and minimum22 values of f on D are called extreme values of f. 10 Example Consider the graphs20 of the functions shown below. What are the extreme values of the p 8 functions; h(x) = x2 and g18 (x) = − x ? 16 6 14 h(x) = x2 4 12 10 2 8 6 – 5 5 10 15 4 g(x) = – x – 2 2 – 4 15 – 10 – 5 5 10 15 – 2 – 6 – 4 Extreme Value Theorem If f is continuous on a closed interval [a; b], then f attains both an – 8 absolute maximum value – 6M and an absolute minimum value m in [a; b]. That is, there are numbers – 8 c and d in [a; b] with f(c) = M and f(d) = m and m ≤ f–(10x) ≤ M for every other x in [a; b].
    [Show full text]
  • MATH 1300: Calculus I 4.2 & 4.3 Part I, Absolute and Local Extrema
    MATH 1300: Calculus I 4.2 & 4.3 Part I, Absolute and Local Extrema Objectives: • Find local maxima and minima of a function graphically. • Find the absolute maximum and the absolute minimum of a function graphically. • Use the first derivative test to find local extrema analytically. Definitions: • CRITICAL NUMBER: A number c in the domain of a function f is a critical number of f if f 0(c) = 0 f 0(c) does not exist. • ABSOLUTE MAXIMUM VALUE: For a number c in the domain of a function f, the number f(c) is the absolute maximum value of f(x) if f(c) ≥ f(x) for all x in the domain of f: • ABSOLUTE MINIMUM VALUE: For a number c in the domain of a function f, the number f(c) is the absolute minimum value of f(x) if f(c) ≤ f(x) for all x in the domain of f: We refer to absolute maximum and minimum values as absolute extrema . Functions don't always have absolute extrema. Which of these functions have absolute extrema? a b a b a b a b a b You will work more with absolute extrema in your project tomorrow! 1 MATH 1300: Calculus I 4.2 & 4.3 Part I, Absolute and Local Extrema Definitions: • LOCAL MAXIMUM VALUE: The number f(c) is a local maximum value of f(x) if f(c) ≥ f(x) when x is near c: • LOCAL MINIMUM VALUE: The number f(c) is a local minimum value of f(x) if f(c) ≤ f(x) when x is near c: We refer to local maximums and minimums as local extrema .
    [Show full text]