Astronomical Evidence for an Alternative to Dark Matter?
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

190 Index of Names
Index of names Ancora Leonis 389 NGC 3664, Arp 005 Andriscus Centauri 879 IC 3290 Anemodes Ceti 85 NGC 0864 Name CMG Identification Angelica Canum Venaticorum 659 NGC 5377 Accola Leonis 367 NGC 3489 Angulatus Ursae Majoris 247 NGC 2654 Acer Leonis 411 NGC 3832 Angulosus Virginis 450 NGC 4123, Mrk 1466 Acritobrachius Camelopardalis 833 IC 0356, Arp 213 Angusticlavia Ceti 102 NGC 1032 Actenista Apodis 891 IC 4633 Anomalus Piscis 804 NGC 7603, Arp 092, Mrk 0530 Actuosus Arietis 95 NGC 0972 Ansatus Antliae 303 NGC 3084 Aculeatus Canum Venaticorum 460 NGC 4183 Antarctica Mensae 865 IC 2051 Aculeus Piscium 9 NGC 0100 Antenna Australis Corvi 437 NGC 4039, Caldwell 61, Antennae, Arp 244 Acutifolium Canum Venaticorum 650 NGC 5297 Antenna Borealis Corvi 436 NGC 4038, Caldwell 60, Antennae, Arp 244 Adelus Ursae Majoris 668 NGC 5473 Anthemodes Cassiopeiae 34 NGC 0278 Adversus Comae Berenices 484 NGC 4298 Anticampe Centauri 550 NGC 4622 Aeluropus Lyncis 231 NGC 2445, Arp 143 Antirrhopus Virginis 532 NGC 4550 Aeola Canum Venaticorum 469 NGC 4220 Anulifera Carinae 226 NGC 2381 Aequanimus Draconis 705 NGC 5905 Anulus Grahamianus Volantis 955 ESO 034-IG011, AM0644-741, Graham's Ring Aequilibrata Eridani 122 NGC 1172 Aphenges Virginis 654 NGC 5334, IC 4338 Affinis Canum Venaticorum 449 NGC 4111 Apostrophus Fornac 159 NGC 1406 Agiton Aquarii 812 NGC 7721 Aquilops Gruis 911 IC 5267 Aglaea Comae Berenices 489 NGC 4314 Araneosus Camelopardalis 223 NGC 2336 Agrius Virginis 975 MCG -01-30-033, Arp 248, Wild's Triplet Aratrum Leonis 323 NGC 3239, Arp 263 Ahenea -

Ω Cen 127 M96 = NGC 3377 116 582
INDEX OF OBJECTS Palomar 3 95 Palomar 4 95 Palomar 5 95 CLUSTERS OF GALAXIES Palomar 14 95 85 203 Abell Palomar 15 95 Abell 262 203 47 Tue 155 Abell 1060 203 Abell 1367 181 GALAXIES Abell 1795 189. 203 A0136-080 5, 315 Abell 2029 203 AM2020-5050 315 Abell 2199 203 Arp 220 432 Abell 2256 169-170 Abell 2319 203 Carina 145-147, 158-159, 247-249 Abell 2626 203 Cygnus A 208 AWM 4 167. 169 DDO 127 139, 141-142, 147-148, 152 AWM 7 169. 208 DDO 154 141 Cancer 59 Draco 5, 144-147, 149, 153-155, Canes-Venatici/Ursa Major complex 157-159, 247-249 115 ESO 415-G26 315 Centaurus 110, 168 ESO 474-G20 314 Coma 1, 15, 87, 97, 101, 112, 115, Fornax 5, 144-147, 158-159, 249, 165, 169, 181, 186-187, 283, 351 403, 408 Galaxy, The (Milky Way) 2, 16-20, DC1842-63 59-60 23-25, 33, 36, 39-41, 43-44, 46- Hercules 59 47, 49-50, 87-88, 95, 111, 119, Hickson 88 51-52 122, 127-130, 136, 197, 207, Local Group 43, 50, 100, 115, 250, 213, 237, 248-250, 289, 294-295, 253, 322, 331, 350, 362, 402, 297-298, 301, 322, 327, 331, 435, 439, 539, 541 356, 391, 397-398, 407, 411-413, MKW 4 169 433. 436, 473, 494, 496, 499, MKW 9 169 519, 525, 530-531, 535-536, 540, M96 Group 116 542, 551, 553, 555, 557 Pegasus I 59, 167 Hickson 88a 51-52 Perseus 15, 105, 186, 189, 197, IC 724 59 206-207, 313 IC 2233 416, 418 Sculptor Group 132 Magellanic Clouds 408 Virgo 97-104, 107-108, 110, 115, M31 49-50, 86-87, 127-128, 146, 162, 168, 175, 203, 216, 248, 249-250, 275, 297, 331, 334, 257, 322, 332, 350. -

Bibcode Main Author Title Full Author List 2015A&A...573L...4L Liseau, R
BibCode Main Author Title Full Author list 2015A&A...573L...4L Liseau, R. ALMA observations of α Centauri. First detection of main-sequence stars at 3 mm Liseau, R.; Vlemmings, W.; Bayo, A.; Bertone, E.; Black, J. H.; del Burgo, wavelength C.; Chavez, M.; Danchi, W.; De la Luz, V.; Eiroa, C.; Ertel, S.; Fridlund, M. C. W.; Justtanont, K.; Krivov, A.; Marshall, J. P.; Mora, A.; Montesinos, B.; Nyman, L. -A.; Olofsson, G.; Sanz-Forcada, J.; Thébault, P.; White, G. J. 2015A&A...575A..19R Riviere-Marichalar, P. Herschel-PACS observations of [OI] and H<SUB>2</SUB>O in Chamaeleon II Riviere-Marichalar, P.; Bayo, A.; Kamp, I.; Vicente, S.; Williams, J. P.; Barrado, D.; Eiroa, C.; Duchêne, G.; Montesinos, B.; Mathews, G.; Podio, L.; Dent, W. R. F.; Huélamo, N.; MerÃ-n, B. 2015A&A...575A..51L Liu, C. Quest for the lost siblings of the Sun Liu, C.; Ruchti, G.; Feltzing, S.; MartÃ-nez-Barbosa, C. A.; Bensby, T.; Brown, A. G. A.; Portegies Zwart, S. F. 2015A&A...574A.114V Varenius, E. Subarcsecond international LOFAR radio images of the M82 nucleus at 118 MHz and 154 MHz Varenius, E.; Conway, J. E.; MartÃ--Vidal, I.; Beswick, R.; Deller, A. T.; Wucknitz, O.; Jackson, N.; Adebahr, B.; Pérez-Torres, M. A.; Chyży, K. T.; Carozzi, T. D.; Moldón, J.; Aalto, S.; Beck, R.; Best, P.; Dettmar, R. - J.; van Driel, W.; Brunetti, G.; Brüggen, M.; Haverkorn, M.; Heald, G.; Horellou, C.; Jarvis, M. J.; Morabito, L. K.; Miley, G. K.; Röttgering, H. -

Popular Names of Deep Sky (Galaxies,Nebulae and Clusters) Viciana’S List
POPULAR NAMES OF DEEP SKY (GALAXIES,NEBULAE AND CLUSTERS) VICIANA’S LIST 2ª version August 2014 There isn’t any astronomical guide or star chart without a list of popular names of deep sky objects. Given the huge amount of celestial bodies labeled only with a number, the popular names given to them serve as a friendly anchor in a broad and complicated science such as Astronomy The origin of these names is varied. Some of them come from mythology (Pleiades); others from their discoverer; some describe their shape or singularities; (for instance, a rotten egg, because of its odor); and others belong to a constellation (Great Orion Nebula); etc. The real popular names of celestial bodies are those that for some special characteristic, have been inspired by the imagination of astronomers and amateurs. The most complete list is proposed by SEDS (Students for the Exploration and Development of Space). Other sources that have been used to produce this illustrated dictionary are AstroSurf, Wikipedia, Astronomy Picture of the Day, Skymap computer program, Cartes du ciel and a large bibliography of THE NAMES OF THE UNIVERSE. If you know other name of popular deep sky objects and you think it is important to include them in the popular names’ list, please send it to [email protected] with at least three references from different websites. If you have a good photo of some of the deep sky objects, please send it with standard technical specifications and an optional comment. It will be published in the names of the Universe blog. It could also be included in the ILLUSTRATED DICTIONARY OF POPULAR NAMES OF DEEP SKY. -

Super-Massive Black Hole Scaling Relations and Peculiar Ringed Galaxies
SUPER-MASSIVE BLACK HOLE SCALING RELATIONS AND PECULIAR RINGED GALAXIES A DISSERTATION SUBMITTED TO THE FACULTY OF THE GRADUATE SCHOOL OF THE UNIVERSITY OF MINNESOTA BY BURCIN MUTLU IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY MARC S. SEIGAR June, 2017 c BURCIN MUTLU 2017 ALL RIGHTS RESERVED Acknowledgements There are several people who I would like to acknowledge for directly or indirectly contributing to this dissertation. First and foremost, I would like to acknowledge the guidance and support of my ad- visor, Marc S. Seigar. I am thankful to him for his continuous encouragement, patience, and kindness. I appreciate all his contributions of knowledge, expertise, and time, which were invaluable to my success in graduate school. He has set an example of excellence as a researcher, mentor, and role model. In addition, I would like to thank my dissertation committee, Liliya L. R. Williams, M. Claudia Scarlata, and Robert Lysak, for their insightful input, constructive criticism and direction during the course of this dissertation. I have crossed paths with many collaborators who have influenced and enhanced my research. Patrick Treuthardt has been a collaborator for most of the work during my dissertation. The addition of his scientific point of view has improved the quality of the work in this dissertation tremendously. Our discussions have always been stimulating and rewarding. I am thankful to him for mentoring me and being a dear friend to me. I would also like to thank Benjamin L. Davis for numerous helpful advice and inspiring discussions. He has directly involved with many aspects of Chapter 1. -
DSO List V2 Current
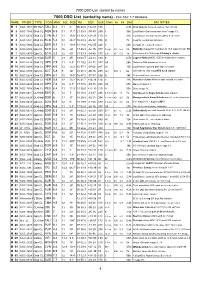
7000 DSO List (sorted by name) 7000 DSO List (sorted by name) - from SAC 7.7 database NAME OTHER TYPE CON MAG S.B. SIZE RA DEC U2K Class ns bs Dist SAC NOTES M 1 NGC 1952 SN Rem TAU 8.4 11 8' 05 34.5 +22 01 135 6.3k Crab Nebula; filaments;pulsar 16m;3C144 M 2 NGC 7089 Glob CL AQR 6.5 11 11.7' 21 33.5 -00 49 255 II 36k Lord Rosse-Dark area near core;* mags 13... M 3 NGC 5272 Glob CL CVN 6.3 11 18.6' 13 42.2 +28 23 110 VI 31k Lord Rosse-sev dark marks within 5' of center M 4 NGC 6121 Glob CL SCO 5.4 12 26.3' 16 23.6 -26 32 336 IX 7k Look for central bar structure M 5 NGC 5904 Glob CL SER 5.7 11 19.9' 15 18.6 +02 05 244 V 23k st mags 11...;superb cluster M 6 NGC 6405 Opn CL SCO 4.2 10 20' 17 40.3 -32 15 377 III 2 p 80 6.2 2k Butterfly cluster;51 members to 10.5 mag incl var* BM Sco M 7 NGC 6475 Opn CL SCO 3.3 12 80' 17 53.9 -34 48 377 II 2 r 80 5.6 1k 80 members to 10th mag; Ptolemy's cluster M 8 NGC 6523 CL+Neb SGR 5 13 45' 18 03.7 -24 23 339 E 6.5k Lagoon Nebula;NGC 6530 invl;dark lane crosses M 9 NGC 6333 Glob CL OPH 7.9 11 5.5' 17 19.2 -18 31 337 VIII 26k Dark neb B64 prominent to west M 10 NGC 6254 Glob CL OPH 6.6 12 12.2' 16 57.1 -04 06 247 VII 13k Lord Rosse reported dark lane in cluster M 11 NGC 6705 Opn CL SCT 5.8 9 14' 18 51.1 -06 16 295 I 2 r 500 8 6k 500 stars to 14th mag;Wild duck cluster M 12 NGC 6218 Glob CL OPH 6.1 12 14.5' 16 47.2 -01 57 246 IX 18k Somewhat loose structure M 13 NGC 6205 Glob CL HER 5.8 12 23.2' 16 41.7 +36 28 114 V 22k Hercules cluster;Messier said nebula, no stars M 14 NGC 6402 Glob CL OPH 7.6 12 6.7' 17 37.6 -03 15 248 VIII 27k Many vF stars 14.. -

Local Superclusters
13-1 How Far Away Is It – Local Superclusters Local Superclusters {Abstract – In this segment of our “How far away is it” video book, we cover the superclusters closest to our supercluster, Virgo. First we discuss the overall structure of the nearest 20 superclusters and illustrate the galactic structures of galaxy filaments, walls and voids including: the Sculuptor void; the Perseus-Pegasus filament; the Fornax, Centaurus, and Sculptor walls as well as the Great Wall or Coma wall. Then we take a look at several of these superclusters and some of the galaxies in each one we examine. We start with the Hydra Supercluster with the Hydra Galaxy Cluster at its center. We examine NGC 2314, a rare double aligned pair of galaxies. We then move to the Centaurus Supercluster with the Centaurus Galaxy Cluster at its center. We then take a look at some of the galaxies in this supercluster including NGC 4603, NGC 4622, the unusual NGC 4650A, and NGC 4696. We then move on to the Perseus-Pisces Supercluster and the Perseus galaxy cluster within it and the remarkable galaxy NGC 1275 within it. Then we cover the Coma Supercluster with the Coma galaxy cluster at its center. We then take a look at the beautiful and wispy galaxy NGC 4921 along with NGC 4911. Next we review the distances to some of the other local superclusters including Hercules, Leo, Shapely, Horologium, and the 1 billion light years distant Corona-Borealis Supercluster. We also cover the unusual peculiar motion superimposed on the normal Hubble flow that all the galaxies within a billion light years have. -

O Personenregister
O Personenregister A alle Zeichnungen von Sylvia Gerlach Abbe, Ernst (1840 – 1904) 100, 109 Ahnert, Paul Oswald (1897 – 1989) 624, 808 Airy, George Biddell (1801 – 1892) 1587 Aitken, Robert Grant (1864 – 1951) 1245, 1578 Alfvén, Hannes Olof Gösta (1908 – 1995) 716 Allen, James Alfred Van (1914 – 2006) 69, 714 Altenhoff, Wilhelm J. 421 Anderson, G. 1578 Antoniadi, Eugène Michel (1870 – 1944) 62 Antoniadis, John 1118 Aravamudan, S. 1578 Arend, Sylvain Julien Victor (1902 – 1992) 887 Argelander, Friedrich Wilhelm August (1799 – 1875) 1534, 1575 Aristarch von Samos (um −310 bis −230) 627, 951, 1536 Aristoteles (−383 bis −321) 1536 Augustus, Kaiser (−62 bis 14) 667 Abbildung O.1 Austin, Rodney R. D. 907 Friedrich W. Argelander B Baade, Wilhelm Heinrich Walter (1893 – 1960) 632, 994, 1001, 1535 Babcock, Horace Welcome (1912 – 2003) 395 Bahtinov, Pavel 186 Baier, G. 408 Baillaud, René (1885 – 1977) 1578 Ballauer, Jay R. (*1968) 1613 Ball, Sir Robert Stawell (1840 – 1913) 1578 Balmer, Johann Jokob (1825 – 1898) 701 Abbildung O.2 Bappu, Manali Kallat Vainu (1927 – 1982) 635 Aristoteles Barlow, Peter (1776 – 1862) 112, 114, 1538 Bartels, Julius (1899 – 1964) 715 Bath, KarlLudwig 104 Bayer, Johann (1572 – 1625) 1575 Becker, Wilhelm (1907 – 1996) 606 Bekenstein, Jacob David (*1947) 679, 1421 Belopolski, Aristarch Apollonowitsch (1854 – 1934) 1534 Benzenberg, Johann Friedrich (1777 – 1846) 910, 1536 Bergh, Sidney van den (*1929) 1166, 1576, 1578 Bertone, Gianfranco 1423 Bessel, Friedrich Wilhelm (1784 – 1846) 628, 630, 1534 Bethe, Hans Albrecht (1906 – 2005) 994, 1010, 1535 Binnewies, Stefan (*1960) 1613 Blandford, Roger David (*1949) 723, 727 Blazhko, Sergei Nikolajewitsch (1870 – 1956) 1293 Blome, HansJoachim 1523 Bobrovnikoff, Nicholas T. -

The COLOUR of CREATION Observing and Astrophotography Targets “At a Glance” Guide
The COLOUR of CREATION observing and astrophotography targets “at a glance” guide. (Naked eye, binoculars, small and “monster” scopes) Dear fellow amateur astronomer. Please note - this is a work in progress – compiled from several sources - and undoubtedly WILL contain inaccuracies. It would therefor be HIGHLY appreciated if readers would be so kind as to forward ANY corrections and/ or additions (as the document is still obviously incomplete) to: [email protected]. The document will be updated/ revised/ expanded* on a regular basis, replacing the existing document on the ASSA Pretoria website, as well as on the website: coloursofcreation.co.za . This is by no means intended to be a complete nor an exhaustive listing, but rather an “at a glance guide” (2nd column), that will hopefully assist in choosing or eliminating certain objects in a specific constellation for further research, to determine suitability for observation or astrophotography. There is NO copy right - download at will. Warm regards. JohanM. *Edition 1: June 2016 (“Pre-Karoo Star Party version”). “To me, one of the wonders and lures of astronomy is observing a galaxy… realizing you are detecting ancient photons, emitted by billions of stars, reduced to a magnitude below naked eye detection…lying at a distance beyond comprehension...” ASSA 100. (Auke Slotegraaf). Messier objects. Apparent size: degrees, arc minutes, arc seconds. Interesting info. AKA’s. Emphasis, correction. Coordinates, location. Stars, star groups, etc. Variable stars. Double stars. (Only a small number included. “Colourful Ds. descriptions” taken from the book by Sissy Haas). Carbon star. C Asterisma. (Including many “Streicher” objects, taken from Asterism. -
Selected Hubble Image Descriptions
Background on HST Images on Lesson Slides Disk • Information given in same order as images in HST directory on lesson slides on disk. • Information taken from STScI's hubblesite.org. • Image numbers from STScI's catalogue. Einstein Cross, Image 1990-20 The European Space Agency's Faint Object Camera on board NASA's Hubble Space Telescope has provided astronomers with the most detailed image ever taken of the gravitational lens G2237 + 0305--sometimes referred to as the "Einstein Cross.” The photograph shows four images of a very distant quasar which has been multiple-imaged by a relatively nearby galaxy acting as a gravitational lens. Black Eye Galaxy, 2004-04 A collision of two galaxies has left a merged star system with an unusual appearance as well as bizarre internal motions. Messier 64 (M64) has a spectacular dark band of absorbing dust in front of the galaxy's bright nucleus, giving rise to its nicknames of the "Black Eye" or "Evil Eye" galaxy. Dusty Spiral Galaxy, NGC 1275, Image 2003-14 A dusty spiral galaxy appears to be rotating on edge, like a pinwheel, as it slides through the larger, bright galaxy NGC 1275, in this HST image. These images show traces of spiral structure accompanied by dramatic dust lanes and bright blue regions that mark areas of active star formation. Face On Galaxy, NGC 4622, Image 2002-03 Astronomers have found a spiral galaxy that may be spinning to the beat of a different cosmic drummer. To the surprise of astronomers, the galaxy, called NGC 4622, appears to be rotating in the opposite direction to what they expected. -

Galaxies Astro 322 Winter 2011 Feb
Galaxies Astro 322 Winter 2011 Feb. 7 Monday, February 7, 2011 normal spirals irregu ellipticals lars lenticulars barred spirals “tuning-fork” diagram Monday, February 7, 2011 Monday, February 7, 2011 Galaxies classification: key differences: total mass, gas/stars ratio, mass-to-light ratio gas/stars ratio is connected with: •flatness of galaxy •current SFR •ages of stellar population, colors of stars •spiral structure Monday, February 7, 2011 Surface brightness, isophote, profile 15 Night sky at 22.7 20 µB 25 30 radius µB R1/4 Vaucouleurs law Monday, February 7, 2011 elliptical galaxies sequence: oblate/prolate classification based on ratio 10 (1-b/a) of galaxy’s isophotes M32 E2 M87 E0p NGC 4660, E7 7 13 10 - 10 Msun M110 E6 Monday, February 7, 2011 elliptical galaxies sequence: oblate/prolate classification based on ratio 10 (1-b/a) of galaxy’s isophotes M32 E2 M87 E0p NGC 4660, E7 7 13 10 - 10 Msun M110 E6 Monday, February 7, 2011 elliptical galaxies sequence: oblate/prolate classification based on ratio 10 (1-b/a) of galaxy’s isophotes M32 E2 M87 E0p NGC 4660, E7 7 13 10 - 10 Msun M110 E6 Monday, February 7, 2011 lenticular galaxies: some dust/gas, no spiral arms NGC 2787 SB0 Spindle galaxy, S0 NGC 4526, SB0 Monday, February 7, 2011 lenticular galaxies: some dust/gas, no spiral arms Cartwheel galaxy (S pec ring) Monday, February 7, 2011 Supergiant ellipticals/lenticular: centrally dominant (cD) more diffuse, larger haloes, more akin to lenticular IC 1101 Galaxy: NGC 1275: cD galaxy + high velocity system 14 diameter 1700 kpc,10 stars origin -

Elliptical Galaxies
Today in Astronomy 142: normal galaxies The Hubble sequence for the shapes of normal galaxies Distribution of mass and light in normal galaxies Dark matter in spiral galaxies Sa galaxy M104 (the Sombrero), by the Hubble Heritage Team (STScI/NASA). 28 March 2013 Astronomy 142, Spring 2013 1 The Hubble sequence Galaxies are classified by shape into the so-called Hubble types, listed here in this “tuning- fork” diagram. Different spiral galaxy types are distinguished by the shapes of their disks and bulges; different ellipticals by their ellipticity. Chaisson and McMillan, SloanAstronomy Digital Today Sky Survey (SDSS) 28 March 2013 Astronomy 142, Spring 2013 2 The Hubble sequence (continued) Hubble originally thought that the shape of a galaxy indicates evolution- ary status, and proposed this “Late type” arrangement of “Early shapes as the type” corresponding evo- lutionary sequence. (We know now that this isn’t right, but the scheme still has utility.) Sloan Digital Sky Survey (SDSS) 28 March 2013 Astronomy 142, Spring 2013 3 M74 (NGC 628), an Sc galaxy Color composite image from the Gemini North observatory 8 m telescope. Note the relatively small bulge, very strong spiral structure, very blue color of the spiral arms, and the dust lanes on the trailing edges of the arms. 28 March 2013 Astronomy 142, Spring 2013 4 M33 (NGC 598), an Sc galaxy Photograph by Tom Davis. Note the diffuse spiral structure, compared to M74. M74 is a grand design spiral galaxy; M33 is a flocculent spiral galaxy. 28 March 2013 Astronomy 142, Spring 2013 5 NGC 1288, an Sb galaxy BVI color composite image from the FORS1 camera on the 8.2 m VLT Antu telescope (European Southern Observatory).