5.61 F17 Lecture 26: Qualitative Molecular Orbital Theory
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Polar Covalent Bonds: Electronegativity
Polar Covalent Bonds: Electronegativity Covalent bonds can have ionic character These are polar covalent bonds Bonding electrons attracted more strongly by one atom than by the other Electron distribution between atoms is not symmetrical Bond Polarity and Electronegativity Symmetrical Covalent Bonds Polar Covalent Bonds C – C + - C – H C – O (non-polar) (polar) Electronegativity (EN): intrinsic ability of an atom to attract the shared electrons in a covalent bond Inductive Effect: shifting of sigma bonded electrons in resppygonse to nearby electronegative atom The Periodic Table and Electronegativity C – H C - Br and C - I (non-pol)lar) (po l)lar) Bond Polarity and Inductive Effect Nonpolar Covalent Bonds: atoms with similar EN Polar Covalent Bonds: Difference in EN of atoms < 2 Ionic Bonds: Difference in EN > 2 C–H bonds, relatively nonpolar C-O, C-X bonds (more electronegative elements) are polar Bonding electrons shift toward electronegative atom C acqqppuires partial positive char g,ge, + Electronegative atom acquires partial negative charge, - Inductive effect: shifting of electrons in a bond in response to EN of nearby atoms Electrostatic Potential Maps Electrostatic potential maps show calculated charge distributions Colors indicate electron- rich (red) and electron- poor (blue ) reg ions Arrows indicate direction of bond polarity Polar Covalent Bonds: Net Dipole Moments Molecules as a whole are often polar from vector summation of individual bond polarities and lone-pair contributions Strongly polar substances soluble in polar solvents like water; nonpolar substances are insoluble in water. Dipole moment ( ) - Net molecular polarity, due to difference in summed charges - magnitude of charge Q at end of molecular dipole times distance r between charges = Q r, in debyes (D), 1 D = 3.336 1030 coulomb meter length of an average covalent bond, the dipole moment would be 1.60 1029 Cm, or 4.80 D. -

Heterocycles 2 Daniel Palleros
Heterocycles 2 Daniel Palleros Heterocycles 1. Structures 2. Aromaticity and Basicity 2.1 Pyrrole 2.2 Imidazole 2.3 Pyridine 2.4 Pyrimidine 2.5 Purine 3. Π-excessive and Π-deficient Heterocycles 4. Electrophilic Aromatic Substitution 5. Oxidation-Reduction 6. DNA and RNA Bases 7. Tautomers 8. H-bond Formation 9. Absorption of UV Radiation 10. Reactions and Mutations Heterocycles 3 Daniel Palleros Heterocycles Heterocycles are cyclic compounds in which one or more atoms of the ring are heteroatoms: O, N, S, P, etc. They are present in many biologically important molecules such as amino acids, nucleic acids and hormones. They are also indispensable components of pharmaceuticals and therapeutic drugs. Caffeine, sildenafil (the active ingredient in Viagra), acyclovir (an antiviral agent), clopidogrel (an antiplatelet agent) and nicotine, they all have heterocyclic systems. O CH3 N HN O O N O CH 3 N H3C N N HN N OH O S O H N N N 2 N O N N O CH3 N CH3 caffeine sildenafil acyclovir Cl S N CH3 N N H COOCH3 nicotine (S)-clopidogrel Here we will discuss the chemistry of this important group of compounds beginning with the simplest rings and continuing to more complex systems such as those present in nucleic acids. Heterocycles 4 Daniel Palleros 1. Structures Some of the most important heterocycles are shown below. Note that they have five or six-membered rings such as pyrrole and pyridine or polycyclic ring systems such as quinoline and purine. Imidazole, pyrimidine and purine play a very important role in the chemistry of nucleic acids and are highlighted. -
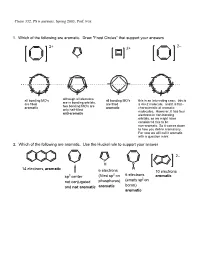
PS 6 Answers, Spring 2003, Prof
Chem 332, PS 6 answers, Spring 2003, Prof. Fox 1. Which of the following are aromatic. Draw "Frost Circles" that support your answers 2– 2+ 2+ + all bonding MO's although all electrons all bonding MO's this is an interesting case: this is are in bonding orbitals, are filled are filled a 4n+2 molecule, and it is flat-- two bonding MO's are aromatic aromatic characteristic of aromatic only half-filled molecules. However, it has four anti-aromatic electrons in non-bonding orbitals, so we might have considered this to be non-aromatic. So it comes down to how you define aromaticity. For now we will call it aromatic with a question mark. 2. Which of the following are aromatic. Use the Huckel rule to support your answer 2– P H B 14 electrons, aromatic H 6 electrons 10 electrons 2 6 electrons sp3 center (filled sp on aromatic (empty sp2 on not conjugated phosphorus) boron) and not aromatic aromatic aromatic 3. Compound 1 has an unusually large dipole moment for an organic hydrocarbon. Explain why (consider resonance structures for the central double bond) We need to remember that for any double bond compound, we can draw two polar resonance structure. Normally, these resonance structures are unimportant unimportant unimportant However, for 1 the story is different because there is a polar resonance form that has two aromatic components. In other words, 'breaking' the double bond gives rise to aromaticity, and therefore the polar resonance structure is important and leads to the observed dipole. dipole 1 8 e– 4 e– 6 e– 6 e– anti- anti- aromatic aromatic aromatic aromatic important resonance unimportant resonance structure structure 5. -

Structure of Benzene, Orbital Picture, Resonance in Benzene, Aromatic Characters, Huckel’S Rule B
Dr.Mrityunjay Banerjee, IPT, Salipur B PHARM 3rd SEMESTER BP301T PHARMACEUTICAL ORGANIC CHEMISTRY –II UNIT I UNIT I Benzene and its derivatives 10 Hours A. Analytical, synthetic and other evidences in the derivation of structure of benzene, Orbital picture, resonance in benzene, aromatic characters, Huckel’s rule B. Reactions of benzene - nitration, sulphonation, halogenationreactivity, Friedelcrafts alkylation- reactivity, limitations, Friedelcrafts acylation. C. Substituents, effect of substituents on reactivity and orientation of mono substituted benzene compounds towards electrophilic substitution reaction D. Structure and uses of DDT, Saccharin, BHC and Chloramine Benzene and its Derivatives Chemists have found it useful to divide all organic compounds into two broad classes: aliphatic compounds and aromatic compounds. The original meanings of the words "aliphatic" (fatty) and "aromatic" (fragrant/ pleasant smell). Aromatic compounds are benzene and compounds that resemble benzene in chemical behavior. Aromatic properties are those properties of benzene that distinguish it from aliphatic hydrocarbons. Benzene: A liquid that smells like gasoline Boils at 80°C & Freezes at 5.5°C It was formerly used to decaffeinate coffee and component of many consumer products, such as paint strippers, rubber cements, and home dry-cleaning spot removers. A precursor in the production of plastics (such as Styrofoam and nylon), drugs, detergents, synthetic rubber, pesticides, and dyes. It is used as a solvent in cleaning and maintaining printing equipment and for adhesives such as those used to attach soles to shoes. Benzene is a natural constituent of petroleum products, but because it is a known carcinogen, its use as an additive in gasoline is now limited. In 1970s it was associated with leukemia deaths. -

Resonance 1. Lone Pair Next to Empty 2P Orbital
1 Lecture 5 Resonance 1. Lone pair next to empty 2p orbital electron pair acceptors - lack of electrons C C CC sp2 R+ is more common sp R+ is less common R+ needs electrons, has to overlap with a. an adjacent 2p lone pair with electrons b. an adjacent pi bond a. an adjacent 2p lone pair with electrons on a neutral atom (+ overall, delocalization of positive charge) R R X = neutral atom with lone pair R R C C R X 2D resonance R X C C R X R X R R R R C R C R CX CX R N R N R 3D resonance R R R R R R R C R C R CX R O CX 3D resonance R O R R R R C better, more bonds, full octets C R F R F b. an adjacent 2p lone pair with electrons on a negative atom (neutral overall, delocalization of electrons) R R X =anion with lone pair R R C C R X 2D resonance R X C C R X R X R R R R C R C R CX CX R C R C R 3D resonance R R R R R R R C R C R CX R N CX 3D resonance R N R R R R C C better, more bonds, full octets R O R O 2 Lecture 5 Problem 1 – All of the following examples demonstrate delocalization of a lone pair of electrons into an empty 2p orbital. Usually in organic chemistry this is a carbocation site, but not always. -

Evaluation of Gaussian Molecular Integrals I
The Mathematica® Journal Evaluation of Gaussian Molecular Integrals I. Overlap Integrals Minhhuy Hô Julio Manuel Hernández-Pérez This article discusses the evaluation of molecular overlap integrals for Gaussian-type functions with arbitrary angular dependence. As an example, we calculate the overlap matrix for the water molecule in the STO-3G basis set. ‡ Introduction Computational quantum chemistry makes extensive use of various integrals (and their derivatives) of the general form [1, 2, 3] ¶ ‡ caHrL O cbHrL dr, (1) -¶ where caHrL is an unnormalized Cartesian Gaussian function centered at A = 9Ax, Ay, Az=: 2 ax ay az -a r-A caHr; a, A, aL = Hx - AxL Iy - AyM Hz - AzL e , (2) where A is normally taken at the nucleus, a is the orbital exponent, and the polynomial rep- resents the angular part, in that the sum of the Cartesian angular momenta ax + ay + az = 0, 1, 2, … corresponds to functions of type s, p, d, f, …. When the operator O is 1, one simply has the overlap/density integral; otherwise it can be the energy operator for kinetic energy - 1 2, electron-nuclear attraction r - R -1, or electron-electron 2 ! -1 repulsion ri - rj (which would involve double integrals). Other molecular properties involving external fields (response functions) or transition moments can also be computed from integrals of this form. The Mathematica Journal 14 © 2012 Wolfram Media, Inc. 2 Minhhuy Hô and Julio Manuel Hernández-Pérez · Gaussian-Type Functions Gaussian-type functions are not the most natural choice for expanding the wavefunction. Slater-type functions, where the exponent is -a r - A instead, can describe atomic systems more realistically. -

Physics of Resonating Valence Bond Spin Liquids Julia Saskia Wildeboer Washington University in St
Washington University in St. Louis Washington University Open Scholarship All Theses and Dissertations (ETDs) Summer 8-13-2013 Physics of Resonating Valence Bond Spin Liquids Julia Saskia Wildeboer Washington University in St. Louis Follow this and additional works at: https://openscholarship.wustl.edu/etd Recommended Citation Wildeboer, Julia Saskia, "Physics of Resonating Valence Bond Spin Liquids" (2013). All Theses and Dissertations (ETDs). 1163. https://openscholarship.wustl.edu/etd/1163 This Dissertation is brought to you for free and open access by Washington University Open Scholarship. It has been accepted for inclusion in All Theses and Dissertations (ETDs) by an authorized administrator of Washington University Open Scholarship. For more information, please contact [email protected]. WASHINGTON UNIVERSITY IN ST. LOUIS Department of Physics Dissertation Examination Committee: Alexander Seidel, Chair Zohar Nussinov Michael C. Ogilvie Jung-Tsung Shen Xiang Tang Li Yang Physics of Resonating Valence Bond Spin Liquids by Julia Saskia Wildeboer A dissertation presented to the Graduate School of Arts and Sciences of Washington University in partial fulfillment of the requirements for the degree of Doctor of Philosophy August 2013 St. Louis, Missouri TABLE OF CONTENTS Page LIST OF FIGURES ................................ v ACKNOWLEDGMENTS ............................. ix DEDICATION ................................... ix ABSTRACT .................................... xi 1 Introduction .................................. 1 1.1 Landau’s principle of symmetry breaking and topological order .... 2 1.2 From quantum dimer models to spin models .............. 5 1.2.1 The Rokhsar-Kivelson (RK) point ................ 12 1.3 QDM phase diagrams ........................... 14 1.4 Z2 quantum spin liquid and other topological phases .......... 15 1.4.1 Z2 RVB liquid ........................... 16 1.4.2 U(1) critical RVB liquid .................... -

Physical Organic Chemistry
PHYSICAL ORGANIC CHEMISTRY Yu-Tai Tao (陶雨台) Tel: (02)27898580 E-mail: [email protected] Website:http://www.sinica.edu.tw/~ytt Textbook: “Perspective on Structure and Mechanism in Organic Chemistry” by F. A. Corroll, 1998, Brooks/Cole Publishing Company References: 1. “Modern Physical Organic Chemistry” by E. V. Anslyn and D. A. Dougherty, 2005, University Science Books. Grading: One midterm (45%) one final exam (45%) and 4 quizzes (10%) homeworks Chap.1 Review of Concepts in Organic Chemistry § Quantum number and atomic orbitals Atomic orbital wavefunctions are associated with four quantum numbers: principle q. n. (n=1,2,3), azimuthal q.n. (m= 0,1,2,3 or s,p,d,f,..magnetic q. n. (for p, -1, 0, 1; for d, -2, -1, 0, 1, 2. electron spin q. n. =1/2, -1/2. § Molecular dimensions Atomic radius ionic radius, ri:size of electron cloud around an ion. covalent radius, rc:half of the distance between two atoms of same element bond to each other. van der Waal radius, rvdw:the effective size of atomic cloud around a covalently bonded atoms. - Cl Cl2 CH3Cl Bond length measures the distance between nucleus (or the local centers of electron density). Bond angle measures the angle between lines connecting different nucleus. Molecular volume and surface area can be the sum of atomic volume (or group volume) and surface area. Principle of additivity (group increment) Physical basis of additivity law: the forces between atoms in the same molecule or different molecules are very “short range”. Theoretical determination of molecular size:depending on the boundary condition. -

Localized Electron Model for Bonding What Does Hybridization Mean?
190 Localized electron model for bonding 1. Determine the Lewis Structure for the molecule 2. Determine resonance structures 3. Determine the shape of the molecule 4. Determine the hybridization of the atoms What does hybridization mean? Why hybridize? Look at the shape of many molecules, and compare this to the shape of the orbitals of each of the atoms. Shape of orbitals Orbitals on atoms are s, p, d, and f, and there are certain shapes associated with each orbital. an s orbital is a big sphere the f orbitals look like two four leaf the p orbitals looks like “8” ’s clovers each one points in along an axis three f orbitals look like weird “8”’s with two doughnuts around each four of the d orbitals look like four one leaf clovers one d orbital looks like an “8” with a doughnut around the middle Shape of molecules Remember we determine the shape of molecules by determining the number of sets of electrons around the atom. count double and triple bonds as one set, count single bonds as one set of electrons and count lone pairs as a set 2 sets—each pair of electrons points 180° away from the other 5 sets—each pair points toward the corner of a trigonal bipyramid 3 sets—each pair points toward the corner of a triangle 6 sets—each pair points toward the corners of an octahedron 4 sets—each pair points toward the corner of a tetrahedron 191 To make bonds we need orbitals—the electrons need to go some where. -

Heterocyclic Chemistrychemistry
HeterocyclicHeterocyclic ChemistryChemistry Professor J. Stephen Clark Room C4-04 Email: [email protected] 2011 –2012 1 http://www.chem.gla.ac.uk/staff/stephenc/UndergraduateTeaching.html Recommended Reading • Heterocyclic Chemistry – J. A. Joule, K. Mills and G. F. Smith • Heterocyclic Chemistry (Oxford Primer Series) – T. Gilchrist • Aromatic Heterocyclic Chemistry – D. T. Davies 2 Course Summary Introduction • Definition of terms and classification of heterocycles • Functional group chemistry: imines, enamines, acetals, enols, and sulfur-containing groups Intermediates used for the construction of aromatic heterocycles • Synthesis of aromatic heterocycles • Carbon–heteroatom bond formation and choice of oxidation state • Examples of commonly used strategies for heterocycle synthesis Pyridines • General properties, electronic structure • Synthesis of pyridines • Electrophilic substitution of pyridines • Nucleophilic substitution of pyridines • Metallation of pyridines Pyridine derivatives • Structure and reactivity of oxy-pyridines, alkyl pyridines, pyridinium salts, and pyridine N-oxides Quinolines and isoquinolines • General properties and reactivity compared to pyridine • Electrophilic and nucleophilic substitution quinolines and isoquinolines 3 • General methods used for the synthesis of quinolines and isoquinolines Course Summary (cont) Five-membered aromatic heterocycles • General properties, structure and reactivity of pyrroles, furans and thiophenes • Methods and strategies for the synthesis of five-membered heteroaromatics -

HETEROLEPTIC PADDLEWHEEL COMPLEXES and MOLECULAR ASSEMBLIES of DIMOLYBDENUM and DITUNGSTEN: a Study of Electronic and Structural Control
HETEROLEPTIC PADDLEWHEEL COMPLEXES AND MOLECULAR ASSEMBLIES OF DIMOLYBDENUM AND DITUNGSTEN: A Study of Electronic and Structural Control DISSERTATION Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By DOUGLAS J. BROWN, B.S., M.S. ***** The Ohio State University 2006 Dissertation Committee: Approved by Professor MALCOLM H. CHISHOLM, Advisor Professor CLAUDIA TURRO _________________________________ Professor CHRISTOPHER M. HADAD Advisor Graduate Program in Chemistry ABSTRACT Molybdenum and tungsten have a rich chemistry in quadruply-bonded paddlewheel complexes that are very similar in many ways, yet significantly different in other ways. Details and findings from Density Functional Theory studies of homoleptic and heteroleptic ligand complexes as well as simple pairs of dimers linked by a bifunctional oxalate bridge are discussed. Special interest is given to metal-to-ligand interactions in paddlewheel complexes and metal-to-bridge interactions in simple pairs of dimers. Computational studies provide great insight, reliable explanations, and qualitative predictions of physicochemical properties. A new series of dimolybdenum and ditungsten paddlewheel complexes with i i mixed amidinate-carboxylate ligands of the form trans-M2(O2CCH3)2( PrNC(R)N Pr)2 where M = Mo, W and R = Me, C≡CtBu, C≡CPh, or C≡CFc have been synthesized and characterized with the exception of the tungsten complex where R = Me. The synthesis of a series of complexes with each metal allowed for the analysis and comparison of molecular structural features, spectroscopic properties, and electrochemical behavior. The dinuclear centers exhibit redox chemistry which is dependent upon the nature of the ancillary ligand, and the electrochemical properties can be tuned through ligand ii modifications. -

Molecular Orbital Description of the Allyl Radical
Chapter 13 Conjugated Unsaturated Systems 13.1) Introduction: §Conjugated unsaturated systems have a p orbital on a carbon adjacent to a double bond. ·The p orbital can come from another double or triple bond ·The p orbital may be the empty p orbital of a carbocation or a p orbital with a single electron in it (a radical) ·Conjugation affords special stability to the molecule ·Conjugated molecules can be detected using UV spectroscopy. 13.2) Allylic Substitution and the Allylic Radical: §Reaction of propene with bromine varies depending on reaction conditions ·At low temperature the halogen adds across the double bond ·At high temperature or at very low concentration of halogen an allylic substitution occurs l Allylic Chlorination (High Temperature): § Allylic chlorination can be performed at high temperature in the gas phase 73 PDF Creator - PDF4Free v2.0 http://www.pdf4free.com § The reaction is a free radical chain reaction, including initiation step, first propagation and second propagation steps. § The relative stability of some carbon radicals is as follows: This trend is reflected in their respective C-H bond dissociation energies l Allylic Bromination with N-Bromosuccinimide: § Propene undergoes allylic bromination with N- bromosuccinimide (NBS) in the presence of light or peroxides. NBS provides a continuous low concentration of bromine for the radical reaction, which favors allylic substitution over alkene addition. 74 PDF Creator - PDF4Free v2.0 http://www.pdf4free.com §The radical reaction is initiated by a small amount of