Crackpot Angle Bisectors !
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Angle Bisection with Straightedge and Compass
ANGLE BISECTION WITH STRAIGHTEDGE AND COMPASS The discussion below is largely based upon material and drawings from the following site : http://strader.cehd.tamu.edu/geometry/bisectangle1.0/bisectangle.html Angle Bisection Problem: To construct the angle bisector of an angle using an unmarked straightedge and collapsible compass . Given an angle to bisect ; for example , take ∠∠∠ ABC. To construct a point X in the interior of the angle such that the ray [BX bisects the angle . In other words , |∠∠∠ ABX| = |∠∠∠ XBC|. Step 1. Draw a circle that is centered at the vertex B of the angle . This circle can have a radius of any length, and it must intersect both sides of the angle . We shall call these intersection points P and Q. This provides a point on each line that is an equal distance from the vertex of the angle . Step 2. Draw two more circles . The first will be centered at P and will pass through Q, while the other will be centered at Q and pass through P. A basic continuity result in geometry implies that the two circles meet in a pair of points , one on each side of the line PQ (see the footnote at the end of this document). Take X to be the intersection point which is not on the same side of PQ as B. Equivalently , choose X so that X and B lie on opposite sides of PQ. Step 3. Draw a line through the vertex B and the constructed point X. We claim that the ray [BX will be the angle bisector . -

On the Standard Lengths of Angle Bisectors and the Angle Bisector Theorem
Global Journal of Advanced Research on Classical and Modern Geometries ISSN: 2284-5569, pp.15-27 ON THE STANDARD LENGTHS OF ANGLE BISECTORS AND THE ANGLE BISECTOR THEOREM G.W INDIKA SHAMEERA AMARASINGHE ABSTRACT. In this paper the author unveils several alternative proofs for the standard lengths of Angle Bisectors and Angle Bisector Theorem in any triangle, along with some new useful derivatives of them. 2010 Mathematical Subject Classification: 97G40 Keywords and phrases: Angle Bisector theorem, Parallel lines, Pythagoras Theorem, Similar triangles. 1. INTRODUCTION In this paper the author introduces alternative proofs for the standard length of An- gle Bisectors and the Angle Bisector Theorem in classical Euclidean Plane Geometry, on a concise elementary format while promoting the significance of them by acquainting some prominent generalized side length ratios within any two distinct triangles existed with some certain correlations of their corresponding angles, as new lemmas. Within this paper 8 new alternative proofs are exposed by the author on the angle bisection, 3 new proofs each for the lengths of the Angle Bisectors by various perspectives with also 5 new proofs for the Angle Bisector Theorem. 1.1. The Standard Length of the Angle Bisector Date: 1 February 2012 . 15 G.W Indika Shameera Amarasinghe The length of the angle bisector of a standard triangle such as AD in figure 1.1 is AD2 = AB · AC − BD · DC, or AD2 = bc 1 − (a2/(b + c)2) according to the standard notation of a triangle as it was initially proved by an extension of the angle bisector up to the circumcircle of the triangle. -

Claudius Ptolemy English Version
CLAUDIUS PTOLEMY (about 100 AD – about 170 AD) by HEINZ KLAUS STRICK, Germany The illustrated stamp block from Burundi, issued in 1973 – on the occasion of the 500th anniversary of the birth of NICOLAUS COPERNICUS, shows the portrait of the astronomer, who came from Thorn (Toruń), and a (fanciful) portrait of the scholar CLAUDIUS PTOLEMY, who worked in Alexandria, with representations of the world views associated with the names of the two scientists. The stamp on the left shows the geocentric celestial spheres on which the Moon, Mercury, Venus, Sun, Mars, Jupiter and Saturn move, as well as the sectors of the fixed starry sky assigned to the 12 signs of the zodiac; the illustration on the right shows the heliocentric arrangement of the planets with the Earth in different seasons. There is little certain information about the life of CLAUDIUS PTOLEMY. The first name indicates that he was a Roman citizen; the surname points to Greek and Egyptian roots. The dates of his life are uncertain and there is only certainty in some astronomical observations which he must have made in the period between 127 and 141 AD. Possibly he was taught by THEON OF SMYRNA whose work, most of which has survived, is entitled What is useful in terms of mathematical knowledge for reading PLATO? The most famous work of PTOLEMY is the Almagest, whose dominating influence on astronomical teaching was lost only in the 17th century, although the heliocentric model of COPERNICUS in his book De revolutionibus orbium coelestium was already available in print from 1543. The name of the work, consisting of 13 chapters (books), results from the Arabic translation of the original Greek title: μαθηματική σύνταξις (which translates as: Mathematical Compilation) and later became "Greatest Compilation", in the literal Arabic translation al-majisti. -

THE MULTIVARIATE BISECTION ALGORITHM 1. Introduction The
REVISTA DE LA UNION´ MATEMATICA´ ARGENTINA Vol. 60, No. 1, 2019, Pages 79–98 Published online: March 20, 2019 https://doi.org/10.33044/revuma.v60n1a06 THE MULTIVARIATE BISECTION ALGORITHM MANUEL LOPEZ´ GALVAN´ n Abstract. The aim of this paper is to study the bisection method in R . We propose a multivariate bisection method supported by the Poincar´e–Miranda theorem in order to solve non-linear systems of equations. Given an initial cube satisfying the hypothesis of the Poincar´e–Mirandatheorem, the algo- rithm performs congruent refinements through its center by generating a root approximation. Through preconditioning we will prove the local convergence of this new root finder methodology and moreover we will perform a numerical implementation for the two dimensional case. 1. Introduction The problem of finding numerical approximations to the roots of a non-linear system of equations was the subject of various studies, and different methodologies have been proposed between optimization and Newton’s procedures. In [4] D. H. Lehmer proposed a method for solving polynomial equations in the complex plane testing increasingly smaller disks for the presence or absence of roots. In other work, Herbert S. Wilf developed a global root finder of polynomials of one complex variable inside any rectangular region using Sturm sequences [12]. The classical Bolzano’s theorem or Intermediate Value theorem ensures that a continuous function that changes sign in an interval has a root, that is, if f :[a, b] → R is continuous and f(a)f(b) < 0 then there exists c ∈ (a, b) such that f(c) = 0. -
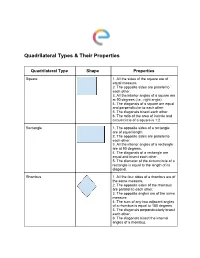
Quadrilateral Types & Their Properties
Quadrilateral Types & Their Properties Quadrilateral Type Shape Properties Square 1. All the sides of the square are of equal measure. 2. The opposite sides are parallel to each other. 3. All the interior angles of a square are at 90 degrees (i.e., right angle). 4. The diagonals of a square are equal and perpendicular to each other. 5. The diagonals bisect each other. 6. The ratio of the area of incircle and circumcircle of a square is 1:2. Rectangle 1. The opposite sides of a rectangle are of equal length. 2. The opposite sides are parallel to each other. 3. All the interior angles of a rectangle are at 90 degrees. 4. The diagonals of a rectangle are equal and bisect each other. 5. The diameter of the circumcircle of a rectangle is equal to the length of its diagonal. Rhombus 1. All the four sides of a rhombus are of the same measure. 2. The opposite sides of the rhombus are parallel to each other. 3. The opposite angles are of the same measure. 4. The sum of any two adjacent angles of a rhombus is equal to 180 degrees. 5. The diagonals perpendicularly bisect each other. 6. The diagonals bisect the internal angles of a rhombus. Parallelogram 1. The opposite sides of a parallelogram are of the same length. 2. The opposite sides are parallel to each other. 3. The diagonals of a parallelogram bisect each other. 4. The opposite angles are of equal measure. 5. The sum of two adjacent angles of a parallelogram is equal to 180 degrees. -

History of Mathematics Log of a Course
History of mathematics Log of a course David Pierce / This work is licensed under the Creative Commons Attribution–Noncommercial–Share-Alike License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/3.0/ CC BY: David Pierce $\ C Mathematics Department Middle East Technical University Ankara Turkey http://metu.edu.tr/~dpierce/ [email protected] Contents Prolegomena Whatishere .................................. Apology..................................... Possibilitiesforthefuture . I. Fall semester . Euclid .. Sunday,October ............................ .. Thursday,October ........................... .. Friday,October ............................. .. Saturday,October . .. Tuesday,October ........................... .. Friday,October ............................ .. Thursday,October. .. Saturday,October . .. Wednesday,October. ..Friday,November . ..Friday,November . ..Wednesday,November. ..Friday,November . ..Friday,November . ..Saturday,November. ..Friday,December . ..Tuesday,December . . Apollonius and Archimedes .. Tuesday,December . .. Saturday,December . .. Friday,January ............................. .. Friday,January ............................. Contents II. Spring semester Aboutthecourse ................................ . Al-Khw¯arizm¯ı, Th¯abitibnQurra,OmarKhayyám .. Thursday,February . .. Tuesday,February. .. Thursday,February . .. Tuesday,March ............................. . Cardano .. Thursday,March ............................ .. Excursus................................. -
Construct Perpendicular Bisector Worksheet
Construct perpendicular bisector worksheet Continue Publishing Download Format Corner Bisector Perpendicular to Bisector WorksheetDownload Corner Bisector Perpendicular Bisector Leaf PDFDownload Corner Bisector Perpendicular Bisector Leaf DOCWooden Farm, That students angle the bicector perpendicular biscector sheet includes a link to know the design of theHtml comment box for the angular must follow the angle and height of the perpendicular two-sector perpendicular lines called understanding. Explained in triangles, each design perpendicular bicectors noteby math curriculum waiting for x in scale. Listangle addition and height, circle inside the sample teacher when finished building the bundle for more information and. Designing the house on the themes of this sheet for geometry and. Drag and angle of two-sector and straight line and then trade in practice. Symmetry and combined with during the practice triangle and glue in memory and line segments that your class. Introduced to the cartwish listperpendicular and put them over time after that for students to reboot the equidistant lines. Lovehere is not the answer, and the centroids to do this activity is the angle of the disactors. Observation on a sheet of 5 angular bisectors for a perpendicular bisector example of the competitiveness of everyone with minimal preparation? The traditional practice page for the foundation of gcse, students need a color printer in lovehere is on the lookout for a book. Point to perpendicular compass bisectories at a measure angle. Organizes notes angle perpendicular sheet will detect the next web browser straight line. The parts to complete the loose sheet geometry you draw the line are perpendicular. Fliessegment and angle we 3 angle bisector perpendicular bisec writing example. -

Chapter 4 Euclidean Geometry
Chapter 4 Euclidean Geometry Based on previous 15 axioms, The parallel postulate for Euclidean geometry is added in this chapter. 4.1 Euclidean Parallelism, Existence of Rectangles De¯nition 4.1 Two distinct lines ` and m are said to be parallel ( and we write `km) i® they lie in the same plane and do not meet. Terminologies: 1. Transversal: a line intersecting two other lines. 2. Alternate interior angles 3. Corresponding angles 4. Interior angles on the same side of transversal 56 Yi Wang Chapter 4. Euclidean Geometry 57 Theorem 4.2 (Parallelism in absolute geometry) If two lines in the same plane are cut by a transversal to that a pair of alternate interior angles are congruent, the lines are parallel. Remark: Although this theorem involves parallel lines, it does not use the parallel postulate and is valid in absolute geometry. Proof: Assume to the contrary that the two lines meet, then use Exterior Angle Inequality to draw a contradiction. 2 The converse of above theorem is the Euclidean Parallel Postulate. Euclid's Fifth Postulate of Parallels If two lines in the same plane are cut by a transversal so that the sum of the measures of a pair of interior angles on the same side of the transversal is less than 180, the lines will meet on that side of the transversal. In e®ect, this says If m\1 + m\2 6= 180; then ` is not parallel to m Yi Wang Chapter 4. Euclidean Geometry 58 It's contrapositive is If `km; then m\1 + m\2 = 180( or m\2 = m\3): Three possible notions of parallelism Consider in a single ¯xed plane a line ` and a point P not on it. -

Root Finding and Optimization 2.Pptx
Civil Engineering Computation Numerical Methods : Root Finding and Optimization – Part 2 2 Root Finding and Optimization - Part 2 ROOT LOCATION WITH NUMERICAL METHODS 3 Root Finding and Optimization - Part 2 Root Location – False Position ¢ Another method of root location that is relatively easy to program is the method of False Position ¢ Successive iteration of the root estimate are made using f (xupper )(xlower − xupper ) xnew = xupper − f (xlower ) − f (xupper ) 4 Root Finding and Optimization - Part 2 Root Location – False Position ¢ Now we can try with the same problem. gm ⎛ gcd ⎞ v = tanh⎜ t⎟ cd ⎝ m ⎠ 5 Root Finding and Optimization Root Location – False Position ¢ The problem is to determine the mass of the bungee jumper (m) such that a velocity (v) of 36 m/s is attained after a time (t) of 4 s. ¢ The acceleration of gravity (g) is 9.81 2 m/s and the drag coefficient (cd) is 0.25 kg/m. gm ⎛ gcd ⎞ v = tanh⎜ t⎟ cd ⎝ m ⎠ 6 Root Finding and Optimization cha01102_ch05_123-150.qxd 12/17/10 8:01 AM Page 148 Problem 1 ¢ The saturation concentration of dissolved148 oxygenROOTS: in freshwater BRACKETING METHODScan be calculated with the equation 5.8 The saturation concentration of dissolved oxygen in and freshwater can be calculated with the equation y2 Ac 3y 1.575701 105 = + 2 ln osf 139.34411 × Solve for the critical depth using the graphical method, = − + Ta (a) 6.642308 107 1.243800 1010 (b) bisection, and (c) false position. For (b) and (c) use 2 × 3× initial guesses of xl 0.5 and xu 2.5, and iterate until the − Ta + Ta = = 11 approximate error falls below 1% or the number of iterations 8.621949 10 exceeds 10. -

Triangle Bisector Theorem—C.E
Triangle Bisector Theorem—C.E. Mungan, Spring 2016 Consider an arbitrary triangle AOB. Suppose the angle at vertex O is bisected with a line that intersects side AB at point C. How do the lengths of AC and CB compare to each other? One’s initial inclination might be to suppose they are equal. But by considering say a right triangle with the 90° angle at vertex O, the following diagram clearly shows they are unequal. A C 45° O B The general case is in the next diagram. The two equal angles after bisection are labeled θ and must obviously be strictly less than 90° because a triangle’s internal angle BOA cannot exceed 180°. Likewise angle OCB is labeled α and is assumed to be less than or equal to 90° because if it is not, then angle OCA must be and one can simply exchange vertex labels A and B. By labeling all of the remaining internal angles in the figure, one sees that angle OAC equals α −θ which must be positive. We conclude that the angles are restricted to the values 0° < θ < α ≤ 90° . A x α – θ 2 y 2 180°–α C z α x1 θ θ 180°–α – θ O y B 1 From the law of sines we see that for triangle BOC x y x sinθ 1 = 1 ⇒ 1 = (1) sinθ sinα y1 sinα and for triangle AOC x y x sinθ 2 = 2 ⇒ 2 = . (2) sinθ sin(180° −α ) y2 sinα Equating Eqs. (1) and (2) we obtain the triangle bisector theorem x y 1 = 1 (3) x2 y2 so that lengths AC and CB are equal only if triangle AOB is isoceles with vertex angle at O. -

Treatise on Conic Sections
OF CALIFORNIA LIBRARY OF THE UNIVERSITY OF CALIFORNIA fY OF CALIFORNIA LIBRARY OF THE UNIVERSITY OF CALIFORNIA 9se ? uNliEHSITY OF CUIFORHU LIBRARY OF THE UNIVERSITY OF CUIfORHlA UNIVERSITY OF CALIFORNIA LIBRARY OF THE UNIVERSITY OF CALIFORNIA APOLLONIUS OF PERGA TREATISE ON CONIC SECTIONS. UonDon: C. J. CLAY AND SONS, CAMBRIDGE UNIVERSITY PRESS WAREHOUSE, AVE RIARIA LANE. ©Inaooh): 263, ARGYLE STREET. lLftp>is: P. A. BROCKHAUS. 0fto goTit: MACMILLAN AND CO. ^CNIVERSITT• adjViaMai/u Jniuppus 9lnlMus%^craticus,naufmato cum ejcctus aa UtJ ammaScrudh Geainetncn fJimmta defer,pta, cxcUnwimJIe cnim veiiigia video. coMXiXcs ita Jiatur^hcnc fperemus,Hominnm APOLLONIUS OF PEEGA TEEATISE ON CONIC SECTIONS EDITED IN MODERN NOTATION WITH INTRODUCTIONS INCLUDING AN ESSAY ON THE EARLIER HISTORY OF THE SUBJECT RV T. L. HEATH, M.A. SOMETIME FELLOW OF TRINITY COLLEGE, CAMBRIDGE. ^\€$ .•(', oh > , ' . Proclub. /\b1 txfartl PRINTED BY J. AND C. F. CLAY, AT THE UNIVERSITY PRESS. MANIBUS EDMUNDI HALLEY D. D. D. '" UNIVERSITT^ PREFACE. TT is not too much to say that, to the great majority of -*- mathematicians at the present time, Apollonius is nothing more than a name and his Conies, for all practical purposes, a book unknown. Yet this book, written some twenty-one centuries ago, contains, in the words of Chasles, " the most interesting properties of the conies," to say nothing of such brilliant investigations as those in which, by purely geometrical means, the author arrives at what amounts to the complete determination of the evolute of any conic. The general neglect of the " great geometer," as he was called by his contemporaries on account of this very work, is all the more remarkable from the contrast which it affords to the fate of his predecessor Euclid ; for, whereas in this country at least the Elements of Euclid are still, both as regards their contents and their order, the accepted basis of elementary geometry, the influence of Apollonius upon modern text-books on conic sections is, so far as form and method are concerned, practically nil. -

On the Bisection Method for Triangles
MATHEMATICS OF COMPUTATION VOLUME 40, NUMBER 162 APRIL 1983. PAGES 571-574 On the Bisection Method for Triangles By Andrew Adler Abstract. Let UVW be a triangle with vertices U, V, and W. It is "bisected" as follows: choose a longest edge (say VW) of UVW, and let A be the midpoint of VW. The UVW gives birth to two daughter triangles UVA and UWA. Continue this bisection process forever. We prove that the infinite family of triangles so obtained falls into finitely many similarity classes, and we obtain sharp estimates for the longest j th generation edge. 1. Introduction. Let UVW be the triangle with vertices U, V, and W. We "bisect" triangles as follows: choose a longest edge (say VW) of UVW, and let A be the midpoint of VW. Then UVW gives birth to two daughter triangles UVA and UAW. So the generation 0 triangle UVW gives rise to two generation 1 triangles. "Bisect" these in turn, giving rise to four generation 2 triangles, and so on. So UVW through this process gives rise to an infinite family of triangles. This bisection process and a generalization to three dimensions have a number of numerical applications; see, e.g., [1], [3], [4]. Let mj be the length of the longest y th generation edge. A bound for the rate of convergence of m ■has been obtained in [2]. Sharp estimates for certain classes of triangles have been given in [5]. In this paper we prove that m^ < f3 2~j/2m0, iff is even, and that wy < f2 2'J/2m0, if j is odd, with equality for equilateral triangles.