Reservoir Computing Using Non-Uniform Binary Cellular Automata
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Apparent Entropy of Cellular Automata
Apparent Entropy of Cellular Automata Bruno Martin Laboratoire d’Informatique et du Parallelisme,´ Ecole´ Normale Superieure´ de Lyon, 46, allee´ d’Italie, 69364 Lyon Cedex 07, France We introduce the notion of apparent entropy on cellular automata that points out how complex some configurations of the space-time diagram may appear to the human eye. We then study, theoretically, if possible, but mainly experimentally through natural examples, the relations between this notion, Wolfram’s intuition, and almost everywhere sensitivity to initial conditions. Introduction A radius-r one-dimensional cellular automaton (CA) is an infinite se- quence of identical finite-state machines (indexed by Ÿ) called cells. Each finite-state machine is in a state and these states change simultane- ously according to a local transition function: the following state of the machine is related to its own state as well as the states of its 2r neigh- bors. A configuration of an automaton is the function which associates to each cell a state. We can thus define a global transition function from the set of all the configurations to itself which associates the following configuration after one step of computation. Recently, a lot of articles proposed classifications of CAs [5, 8, 13] but the canonical reference is still Wolfram’s empirical classification [14] which has resisted numerous attempts of formalization. Among the lat- est attempts, some are based on the mathematical definitions of chaos for dynamical systems adapted to CAs thanks to Besicovitch topol- ogy [2, 6] and [11] introduces the almost everywhere sensitivity to initial conditions for this topology and compares this notion with information propagation formalization. -
![Arxiv:1607.02291V3 [Cs.FL] 8 May 2018](https://docslib.b-cdn.net/cover/3689/arxiv-1607-02291v3-cs-fl-8-may-2018-1473689.webp)
Arxiv:1607.02291V3 [Cs.FL] 8 May 2018
Noname manuscript No. (will be inserted by the editor) A Survey of Cellular Automata: Types, Dynamics, Non-uniformity and Applications (Draft version) Kamalika Bhattacharjee · Nazma Naskar · Souvik Roy · Sukanta Das Received: date / Accepted: date Abstract Cellular automata (CAs) are dynamical systems which exhibit complex global be- havior from simple local interaction and computation. Since the inception of cellular au- tomaton (CA) by von Neumann in 1950s, it has attracted the attention of several researchers over various backgrounds and fields for modelling different physical, natural as well as real- life phenomena. Classically, CAs are uniform. However, non-uniformity has also been in- troduced in update pattern, lattice structure, neighborhood dependency and local rule. In this survey, we tour to the various types of CAs introduced till date, the different characteriza- tion tools, the global behaviors of CAs, like universality, reversibility, dynamics etc. Special attention is given to non-uniformity in CAs and especially to non-uniform elementary CAs, which have been very useful in solving several real-life problems. Keywords Cellular Automata (CAs) · Types · Characterization tools · Dynamics · Non-uniformity · Technology Mathematics Subject Classification (2010) 68Q80 · 37B15 1 Introduction From the end of the first half of 20th century, a new approach has started to come in scien- tific studies, which after questioning the so called Cartesian analytical approach, says that interconnections among the elements of a system, be it physical, biological, artificial or any other, greatly effect the behavior of the system. In fact, according to this approach, knowing the parts of a system, one can not properly understand the system as a whole. -

Abstract Collection of the 2017 International Symposium on Nonlinear Theory and Its Applications (NOLTA2017)
Abstract Collection of the 2017 International Symposium on Nonlinear Theory and its Applications (NOLTA2017) Cancun International Convention Center, Cancun,´ Mexico December 4–7, 2017. Abstract Collection of NOLTA2017 ⃝C IEICE Japan 2017 Typesetting: Data conversion by the authors. Final processing by T. Tsubone and W. Kurebayashi with LATEX. Printed in Japan 2 Contents Welcome Message from the General Chairs . 6 Technical Program Chair’s Message . 7 Organizing Committee . 8 Technical Program Committee . 9 Advisory Committee . 10 NOLTA Steering Committee . 11 Special Session Organizers . 12 Symposium Information . 14 Symposium Venue . 14 Social Events . 14 Session at a Glance . 16 Abstracts 19 A0L-A Plenary Talk 1 . 19 A1L-A Theory and Learning Applications of Koopman Operator Formalism . 19 A1L-B Systems Theory and its Applications . 20 A1L-C Complex systems, complex networks and bigdata analyses . 21 A1L-D Advanced Theory and Applications Related to Communication Quality . 23 A1L-E Neuromorphic Systems and Electronic Devices 1 . 24 A2L-A Network Function for Physically and Logically Coupled System . 25 A2L-B Circuits and Systems / Analog and digital devices . 26 A2L-C Neural Networks / Biological Engineering . 27 A2L-D Complex Communication Sciences 1 . 28 A2L-E Neuromorphic Systems and Electronic Devices 2 . 29 A3L-A Radio and Optical Wireless Communications 1 . 30 A3L-B Complex Networks and Systems / Image and Signal Processing . 32 A3L-C Laser Dynamics and Complex Photonics 1 . 34 A3L-D-1 Complex Communication Sciences 2 . 35 A3L-D-2 Complex Networks and Systems / Image and Signal Processing . 36 A3L-E-1 Neuromorphic Systems and Electronic Devices 3 . 37 A3L-E-2 Machine Learning / Evolutionary computations . -

Lecture P4: Cellular Automata Arrays Allow Manipulation of Potentially Huge Amounts of Data
Array Review Lecture P4: Cellular Automata Arrays allow manipulation of potentially huge amounts of data. ■ All elements of the same type. – double, int ■ N-element array has elements indexed 0 through N-1. ■ Fast access to arbitrary element. – a[i] ■ Waste of space if array is "sparse." Reaction diffusion textures. Andy Witkin and Michael Kass Princeton University • COS 126 • General Computer Science • Fall 2002 • http://www.Princeton.EDU/~cs126 2 Cellular Automata Applications of Cellular Automata Cellular automata. (singular = cellular automaton) Modern applications. ■ Computer simulations that try to emulate laws of nature. ■ Simulations of biology, chemistry, physics. ■ Simple rules can generate complex patterns. – ferromagnetism according to Ising mode – forest fire propagation – nonlinear chemical reaction-diffusion systems – turbulent flow John von Neumann. (Princeton IAS, 1950s) – biological pigmentation patterns ■ Wanted to create and simulate artificial – breaking of materials life on a machine. – growth of crystals ■ Self-replication. – growth of plants and animals ■ ■ "As simple as possible, but no simpler." Image processing. ■ Computer graphics. ■ Design of massively parallel hardware. ■ Art. 3 4 How Did the Zebra Get Its Stripes? One Dimensional Cellular Automata 1-D cellular automata. ■ Sequence of cells. ■ Each cell is either black (alive) or white (dead). ■ In each time step, update status of each cell, depending on color of nearby cells from previous time step. Example rule. Make cell black at time t if at least one of its proper neighbors was black at time t-1. time 0 time 1 time 2 Synthetic zebra. Greg Turk 5 6 Cellular Automata: Designing the Code Cellular Automata: The Code How to store the row of cells. -
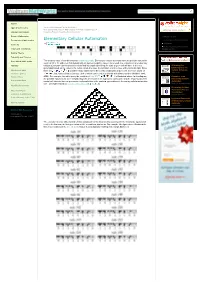
Elementary Cellular Automaton Calculus and Analysis Interactive Entries > Interactive Demonstrations >
Search MathWorld Algebra Applied Mathematics Discrete Mathematics > Cellular Automata > Recreational Mathematics > Mathematical Art > Mathematical Images > elementary cellular automaton Calculus and Analysis Interactive Entries > Interactive Demonstrations > Discrete Mathematics THINGS TO TRY: Foundations of Mathematics Elementary Cellular Automaton elementary cellular automaton 39th prime Geometry do the algebraic units contain History and Terminology Sqrt[2]+Sqrt[3]? Number Theory Probability and Statistics Recreational Mathematics The simplest class of one-dimensional cellular automata. Elementary cellular automata have two possible values for each cell (0 or 1), and rules that depend only on nearest neighbor values. As a result, the evolution of an elementary Topology cellular automaton can completely be described by a table specifying the state a given cell will have in the next A Strategy for generation based on the value of the cell to its left, the value the cell itself, and the value of the cell to its right. Since Exploring k=2, r=2 Alphabetical Index there are possible binary states for the three cells neighboring a given cell, there are a total of Cellular Automata John Kiehl Interactive Entries elementary cellular automata, each of which can be indexed with an 8-bit binary number (Wolfram 1983, Random Entry 2002). For example, the table giving the evolution of rule 30 ( ) is illustrated above. In this diagram, Dynamics of an the possible values of the three neighboring cells are shown in the top row of each panel, and the resulting value the Elementary Cellular New in MathWorld central cell takes in the next generation is shown below in the center. generations of elementary cellular automaton Automaton rule are implemented as CellularAutomaton[r, 1 , 0 , n]. -

Global Properties of Cellular Automata
Global properties of cellular automata Edward Jack Powley Submitted for the qualification of PhD University of York Department of Computer Science October 2009 Abstract A cellular automaton (CA) is a discrete dynamical system, composed of a large number of simple, identical, uniformly interconnected components. CAs were introduced by John von Neumann in the 1950s, and have since been studied extensively both as models of real-world systems and in their own right as abstract mathematical and computational systems. CAs can exhibit emergent behaviour of varying types, including universal computation. As is often the case with emergent behaviour, predicting the behaviour from the specification of the system is a nontrivial task. This thesis explores some properties of CAs, and studies the correlations between these properties and the qualitative behaviour of the CA. The properties studied in this thesis are properties of the global state space of the CA as a dynamical system. These include degree of symmetry, numbers of preimages (convergence of trajectories), and distances between successive states on trajectories. While we do not obtain a complete classifi- cation of CAs according to their qualitative behaviour, we argue that these types of global properties are a better indicator than other, more local, properties. 3 Contents Chapter 1. Introduction 11 Part 1. Literature review 15 Chapter 2. Cellular automata 17 2.1. Definition and dynamics 17 2.2. Example: Conway's Game of Life 19 2.3. 1-dimensional CAs and elementary CAs 21 2.4. Essentially different rules 23 2.5. Classification 26 2.6. Speed of propagation 29 2.7. -

5 Cellular Automata Models
5 Cellular automata models Cellular automata (CA) models epitomize the idea that simple rules can generate complex patterns. A CA consists of an array of cells each with an integer 'state'. On each time step a local update rule is applied to the cells. The update rule defines how the a particular cell will update its state as a funcion of its neighbours state. The CA is run over time and the evolution of the state is observed. 5.1 Elementary cellular automata The elementary one dimensional CA is defined by how three cells influence a single cell. For example, The rules can be expressed in binary form where a 0 represents that a par- ticular configuration gives a white output and a 1 denotes a black output. For example, the above rule in binary is 00011110. Converting this binary number to base-10, we call this rule 30. We thus have a set of different rules for elementary cellular automata from 0 up to 255. 21 Although the rule itself is simple, the output of rule 30 is somewhat compli- cated. 22 23 Elementary CA simulators are easily found on the internet. In the lecture, I will demonstrate one of these written in NetLogo (http://ccl.northwestern.edu/netlogo/). We will look at rules 254, 250, 150, 90, 110, 30 and 193 in this simulator. Some of these rules produce simple repetitive patterns, others produce pe- riodic patterns, while some produce complicated patterns. Rule 30 is of special interest because it is chaotic. This rule is used as the random number generator used for large integers in Mathematica. -

Cellular Automata Can Reduce Memory Requirements of Collective-State Computing Denis Kleyko, E
1 Cellular Automata Can Reduce Memory Requirements of Collective-State Computing Denis Kleyko, E. Paxon Frady, and Friedrich T. Sommer Abstract—Various non-classical approaches of distributed in- include reservoir computing (RC) [2], [3], [4], [5] for buffering formation processing, such as neural networks, computation with spatio-temporal inputs, and attractor networks for associative Ising models, reservoir computing, vector symbolic architectures, memory [6] and optimization [7]. In addition, many other and others, employ the principle of collective-state computing. In this type of computing, the variables relevant in a computation models can be regarded as collective-state computing, such as are superimposed into a single high-dimensional state vector, the random projection [8], compressed sensing [9], [10], randomly collective-state. The variable encoding uses a fixed set of random connected feedforward neural networks [11], [12], and vector patterns, which has to be stored and kept available during symbolic architectures (VSAs) [13], [14], [15]. Interestingly, the computation. Here we show that an elementary cellular these diverse computational models share a fundamental com- automaton with rule 90 (CA90) enables space-time tradeoff for collective-state computing models that use random dense binary monality – they all include an initialization phase in which representations, i.e., memory requirements can be traded off with high-dimensional i.i.d. random vectors or matrices are gener- computation running CA90. We investigate the randomization ated that have to be memorized. behavior of CA90, in particular, the relation between the length of In different models, these memorized random vectors serve the randomization period and the size of the grid, and how CA90 a similar purpose: to represent inputs and variables that need to preserves similarity in the presence of the initialization noise. -

Computational Composition Strategies in Audiovisual Laptop Performance
Computational composition strategies in audiovisual laptop performance Alo Allik The University of Hull This thesis is submitted for the degree of Doctor of Philosophy to accompany a portfolio of audiovisual performances and the software systems used in the creation of these works PhD supervisors: Dr. Robert Mackay and Dr. Joseph Anderson This project was supported by the University of Hull 80th Anniversary Scholarship. April 2014 Acknowledgements I would like to take this opportunity to thank everyone who has supported this project throughout its duration. I am very grateful to my supervisor Rob Mackay who not only has been a very supportive and knowledgeable mentor, but also an amazingly accommodating friend during my time at the Creative Music Technology program at the University Hull Scarborough campus. I am also indebted to my first supervisor Jo Anderson for encouragement, lengthy conversations and in-depth knowledge, particularly in Ambisonic spatializa- tion, allowing me to test the early versions of the Ambisonic Toolkit. This project would not have been possible without the University of Hull funding this project over the course of 3 years and providing means to attend the ISEA symposium in Istanbul. I am grateful for the financial support from the School of Arts and New Media for attending conferences - NIME in Oslo, IFIMPAC in Leeds, and ICMC in Ljubljana - which has provided opportunities to present aspects of this research in the UK and abroad. These experiences proved to be instrumental in shaping the final outcome of this project. I owe a great deal to the dedication and brilliance of the performers and collaborators Andrea Young, Satoshi Shiraishi, and Yota Morimoto, the latter two also for sowing the seeds for my interest and passion for audiovisual per- formances while working together on ibitsu. -

Cellular Automata
Cellular Automata Orit Moskovich 4.12.2013 Outline ´ What is a Cellular Automaton? ´ Wolfram’s Elementary CA ´ Conway's Game of Life ´ Applications and Summary Cellular automaton ´ A discrete model ´ Regular grid of cells, each in one of a finite number of states ´ The grid can be in any finite number of dimensions ´ For each cell, a set of cells called its neighborhood is defined relative to the specified cell Moore von Neumann neighborhood neighborhood Cellular automaton ´ An initial state (time t=0) is selected by assigning a state for each cell ´ A new generation is created (advancing t by 1), according to some fixed rule that determines the new state of each cell in terms of: ´ the current state of the cell ´ the states of the cells in its neighborhood ´ Typically, the rule set is ´ the same for each cell Moore von Neumann ´ does not change over time neighborhood neighborhood ´ applied to the whole grid simultaneously Background Ulam ´ Originally discovered in the 1940s by Stanislaw Ulam and John von Neumann ´ Ulam was studying the growth of crystals and von Neumann was imagining a world of self-replicating robots ´ Studied by some throughout the 1950s and 1960s ´ Conway's Game of Life (1970), a two-dimensional cellular automaton, interest in the subject expanded beyond academia von Neumann ´ In the 1980s, Stephen Wolfram engaged in a systematic study of one- dimensional cellular automata (elementary cellular automata) ´ Wolfram’s research assistant Matthew Cook showed that one of these rules has a VERY cool and important property ´ Wolfram published A New Kind of Science in 2002 and discusses how CA are not simply cool, but are relevant to the study of many fields in science, such as biology, chemistry, physics, computer processors and cryptography, and many more Why the big interest??? ´ A complex system, generated from a very simple configuration ´ Is this even possible? ´ Cellular automata can simulate a variety of real-world systems. -

FINITE-WIDTH ELEMENTARY CELLULAR AUTOMATA 1. Introduction Stephen Wolfram's a New Kind of Science Explores Elementary Cellular
FINITE-WIDTH ELEMENTARY CELLULAR AUTOMATA IAN COLEMAN Abstract. This paper is an empirical study of eight-wide elementary cellu- lar automata motivated by Stephen Wolfram's conjecture about widespread universality in regular elementary cellular automata. Through examples, the concepts of equivalence, reversibility, and additivity in elementary cellular au- tomata are explored. In addition, we will view finite-width cellular automata in the context of finite-size state transition diagrams and develop foundational results about the behavior of finite-width elementary cellular automata. 1. Introduction Stephen Wolfram's A New Kind of Science explores elementary cellular au- tomata and universality in simple computational systems [3]. In 1985, Wolfram conjectured that an elementary cellular automaton could be Turing complete, thus capable of universal computation. At the turn of the century, Matthew Cook pub- lished a proof confirming that a particular cellular automaton, known as \Rule 110," was universal [1]. Wolfram currently conjectures that universality in non-trivial cel- lular automata (and other simple systems) is likely to be extremely common. This paper, in addition to an outline of Wolfram's basic work, is an empirical study seeking to add information and insight to the exploration of elementary cellular automata. Elementary cellular automata have become relevant given Wolfram's develop- ment of the Principle of Computational Equivalence. From Wolfram, the Principle of Computational Equivalence states that \almost all processes that are not ob- viously simple can be viewed as computations of equivalent sophistication [3, p. 5 , 716-717]." Wolfram's MathWorld explains further that \the principle of com- putational equivalence says that systems found in the natural world can perform computations up to a maximal (\universal") level of computational power, and that most systems do in fact attain this maximal level of computational power. -

Design of a Hybrid Programmable 2-D Cellular Automata Based Pseudo Random Number Generator
International Journal of Recent Technology and Engineering (IJRTE ) ISSN: 2277-3878, Volume-8 Issue-6, March 2020 Design of a Hybrid Programmable 2-D Cellular Automata Based Pseudo Random Number Generator Dinakaran P, Gethzi Ahila Poornima I, Paramasivan B concludes the proposed work and suggests a future Abstract: This paper proposes a hybrid programmable enhancement to be undertaken. two-dimensional Cellular Automata (CA) based pseudo-random number generator which includes a newly designed rule set. The II. BACKGROUND properties and evolution of one and two dimensional CA are revisited. The various metrics for evaluating CA as a Cellular Automata is composed of cells. Each of those cells Pseudo-Random Number Generator (PRNG) are discussed. It is contains a finite state machine called ‘automaton’. In the proved that the randomness is high irrespective of the initial seed cellular space, all the cells go from their current state to the by applying this newly designed rule set. The PRNG is tested next state according to the ‘local rule’. These rules govern against a popular statistical test called Diehard test suite and the results show that the PRNG is highly random. The chaotic the transition between states. It is called ‘local’ because it measures like entropy, hamming distance and cycle length have only uses the states of the neighborhood and the current cell been measured as its input. The local transition function is defined as f: Sn→S where n is the size of the neighborhood. For 2-state Keywords : Cellular Automata, Pseudo-Random Number 3-neighborhood CA, the evolution of the ith cell can be Generator, Entropy, Hamming Distance, Programmable CA.